北斗+GPS组合单点定位精度评价与分析

魏二虎，刘学习，刘经南

(1. 武汉大学测绘学院，湖北 武汉 430079; 2. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079)

北斗+GPS组合单点定位精度评价与分析

魏二虎1，刘学习1，刘经南2

(1. 武汉大学测绘学院，湖北 武汉 430079; 2. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079)

北斗系统现在已经进入了全球组网的阶段。本文详细推导了北斗/GPS组合单点定位的数学模型；设计了两种方案，利用Multi-GNSS Experiment(MGEX)网的实测数据，分别从单个测站和亚太及其周边地区的12个测站来全面地进行北斗、GPS单系统，以及北斗+GPS组合单点定位的精度评价与分析；验证了组合单点定位的数学模型，得出了组合系统单点定位的精度和稳定性均优于单系统的结论，以期为北斗系统的应用推广提供参考。

北斗；GPS；单点定位；组合系统；精度评价

由于卫星导航系统具有重大的国家战略意义，同时蕴藏着巨大的国内国际经济利益，因此世界各大工业国无一不在实施或计划自己的卫星导航系统。我国作为目前世界上举足轻重的政治、军事和经济大国当然也不例外，北斗卫星导航系统就是我国目前正在实施、自主研发、独立运行的全球卫星导航定位系统，在国际上被称为BeiDou，目前与美国的GPS、俄罗斯的GLONASS和欧盟的Galileo并列为全球四大GNSS系统。随着这四大系统的逐步完善，未来的导航星座卫星将包含120多颗卫星，并且提供多个无线电频率的信号。多频多模组合定位大大增加了可用卫星的数量，优化了卫星的空间结构，从而进一步提高了定位的精度，因此正在逐步成为研究的热点。

国内外许多专家学者都曾对北斗和GPS组合单点定位作了分析与试验[1-4]。但是有些研究成果均是利用仿真的星座与数据，有些虽然利用实测数据，但是均是分析组合定位在单个测站的性能。很少有文章站在全球的角度，全面地评价与分析北斗与GPS组合定位相对于单一系统的优势。另外，目前北斗卫星导航系统的建设已经完成了第二步，正处于第三步——全球组网的实施阶段[5]。最近几年正是北斗卫星密集发射的阶段，因此有必要经常监测、评价与分析北斗卫星的性能。鉴于此，本文开展北斗与GPS的组合单点定位的研究，以期能够为北斗的应用推广提供参考。

1 北斗+GPS组合单点定位解算模型

1.1 时间基准的统一

GPS时间是GPS系统运作的时间基准，简称为GPST。GPST从本质来说是一种原子时。第一个GPS时开始于1980年1月5日午夜和1月6日凌晨交接的时刻，即UTC时间1980年1月6日的0:00:00。此后，GPST和UTC时的偏差就越来越大，2012年7月1日以后，GPST与UTC之间的差异已经达到16 s，即

GPST≈UTC+16

(1)

式(1)中的近似号是因为GPST和UTC除了由于跳秒累积产生的整秒差异之外，还存在着小于1 μs的秒内偏差，而该偏差可以通过GPS卫星广播星历的UTC时间参数计算得到。

根据2012年12月27日公开的北斗接口控制文档1.0版，BDT以国际单位制秒为基本单位进行时间累积，没有跳秒，因此与GPST一样，BDT是连续时间。BDT的起始历元是UTC时间2006年1月1日00：00：00，对应的儒略日为2 453 736。考虑到BDT起始历元的时刻，GPST的星期数和周内秒计数为：GPST=[1356周，14.000 s]。因此，可以推断出BDT和GPST有如下关系

BDT星期数=GPST星期数+1356

(2)

BDT周内秒计数=GPST周内秒计数+14

(3)

式(3)在计算时需要考虑溢出的问题，即当GPST周内秒数计数+14超过604 800时需要将BDT星期数加1[6]。

1.2 空间基准的统一

由于各个国家在建立各自卫星导航系统的同时，也建立了自己独立的空间基准，因此在进行组合导航定位时一定要统一空间基准。GPS采用的是WGS-84[7]，北斗系统采用的是2000国家大地坐标系(CGCS2000)。这两个坐标系统所定义的原点、尺度、定向及定向演变的尺度都是相同的，它们与IRTF紧密相关。WGS-84最初实现时，精度约为1 m，经过两次优化之后精度已达2 cm，与ITRF精度基本一致，甚至小于WGS-84本身的系统误差。CGCS2000与ITRF的一致性约为5 cm，因此WGS-84与CGCS2000的差异在厘米级[8]。对导航等绝大多数非精密定位应用来讲，WGS-84和CGCS2000这两个空间坐标系通常被认为是相互一致的，它们之间无需任何坐标转换。本文单点定位的精度在米级，因此无需进行两个坐标系统的转换，直接把它们视为同一坐标系即可[9]。

1.3 组合单点定位模型

GNSS伪距定位的方程式如下

(4)

可将式(4)改写成如下的误差校正后的GNSS伪距观测方程式

(5)

(6)

将GPS时间tGPS与BD系统时间tBD之间的差异记为δtGPS-BD，其定义为

δtGPS-BD=tGPS-tBD

(7)

校正后的GPS和BD伪距观测方程式分别为

(8)

(9)

误差校正后的GPS和BD伪距观测值分别为

(10)

(11)

将以上两式线性化后可以建立一个如下的BD/GPS联合定位矩阵方程式

(12)

式(12)中

(13)

(14)

(15)

式(13)中,(x,y,z)为接收机的坐标。利用以上方法即可求出接收机的坐标[11-13]。

2 实测数据处理与分析

由于北斗卫星正在持续建设之中，为了验证近期北斗系统整体定位的效果，本次试验数据采用的是2016年1月8日全球的MGEX网所采集到的北斗和GPS数据。MGEX网测站全球分布如图1所示[14]。由于MGEX网中测站的精确坐标没有发布，因此本文利用Bernese软件中精密单点定位的功能解算出所需测站的ITRF坐标。由于Bernese软件解算出的坐标精度可以达到厘米级至毫米级，而伪距单点定位的精度一般在米级左右，因此解算出的坐标可以作为真值，与利用北斗和GPS组合单点定位算法解算的结果作比较。

图1 MGEX跟踪网全球分布

本文采用两种方案来验证北斗+GPS组合单点定位的性能。

(1) 选择单个测站，分别利用北斗、GPS、北斗+GPS 3种数据解算该测站的坐标。得到该测站全天所有历元解算的结果，精密单点定位的坐标作差，并作比较分析。

(2) 在亚太地区选择12个能同时接收到的北斗和GPS数据的测站，分别利用北斗、GPS和北斗+GPS 3类数据计算测站的坐标。得到每个测站一天的平均值，评价北斗、GPS和北斗+GPS 3种解算方法的性能。

2.1 北斗+GPS在单个测站的性能分析

到目前为止，北斗卫星主要覆盖在亚太地区，且已经能够在这一地区完成导航定位的功能。因此本文选择中国境内jfng测站来进行组合定位的性能分析。利用2016年1月8日jfng全天的数据，分别利用北斗、GPS和北斗+GPS来解算这个测站的坐标。数据采样间隔为30 s，卫星截止高度角为10°。所得到的测站E、N、U方向的均方根误差、卫星平均个数(Num)及PDOP的平均值如图2所示。其中B代表单独利用北斗数据解算的结果，G代表单独利用GPS数据的解算结果，B+G代表利用北斗+GPS组合定位解算的结果(下同)。

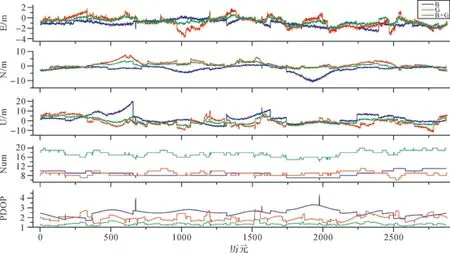
图2 测站jfng E、N、U方向的均方根误差、卫星个数及PDOP值随历元变化

表1给出了利用这3种方法解算所得到的jfng测站东北天3个方向的均方根误差的数值，以及3种方法中全天平均卫星的个数、PDOP的平均值。其中最后一列代表的是北斗+GPS组合定位分别相对于北斗单系统、GPS单系统的提高率。

从图2和表1中可以看出，在E方向上，北斗+GPS组合定位精度最高，与北斗解算相比提高了27.7%，与GPS相比提高了28.6%，北斗解算的精度要高于GPS解算的精度，这与北斗在东西方向上分布5颗GEO卫星有关，大大增强了北斗东西方向的结构强度；在N方向上，北斗+GPS组合定位精度最高，与北斗解算相比提高了51.3%，比GPS提高了37.8%，GPS解算精度要高于北斗解算的精度；在U方向上，北斗+GPS组合定位精度最高，比北斗解算提高了36.5%，比GPS解算提高了31.4%，北斗解算精度要低于GPS解算的精度。利用这3种方法解算，E方向的精度均高于N方向的精度和U方向上的精度。

表1 测站jfng东北天(E、N、U)方向的均方根误差、平均卫星个数及PDOP值

参数BDSGPSBDS+GPS提高率/(%)E/m1.20101.21710.868527.7/28.6N/m2.96952.32701.447551.3/37.8U/m4.71704.36942.996136.5/31.4平均卫星数8.74648.788217.5343100.5/99.5PDOP2.49811.93651.334246.6/31.1

从图2中也可以看出，北斗卫星的稳定性不如GPS，北斗+GPS组合系统的稳定性最高。表1中显示，北斗系统的PDOP值高于GPS，GPS的PDOP值高于组合系统，这是因为虽然北斗系统能够在亚太地区提供定位服务，但是并没有完成全球的组网，卫星分布不如GPS均匀，而组合定位中卫星的个数是比单系统增加了一倍，大大增加了导航卫星的个数，增强了卫星几何图形的空间强度，从而降低了PDOP值。

另外，多系统组合的另一个比较大的优势就是在有遮挡物的情况下，比如在城市峡谷中，低高度角度的卫星被遮挡情况下仍然能够正常运行。因此本文作了如下的试验，计算卫星截止高度角分别为10°、20°、30°、40°的情况下，测站的三维位置均方根误差，定位的稳定率，卫星的平均个数，平均PDOP值。其中，稳定率=成功解算的历元个数/总历元的个数。其结果如图3所示。

图3 测站jfng三维位置均方根误差、稳定率以及平均卫星个数和PDOP值随高度角变化

从图3中可以看出，随着截止卫星高度角的增加，定位的三维位置误差在不断增大，但是组合定位的精度总是高于单系统定位的精度。当截止高度角达到40°以后，单系统三维位置误差会达到25 m左右，而北斗+GPS组合定位的位置误差虽然也在增加，但是在15 m左右，远小于单系统的定位误差。卫星截止高度角在30°以下时，对解算的稳定率影响不大，继续增加卫星截止高度角，单系统稳定性急剧下降，而北斗+GPS定位的稳定性依然很高。这是因为虽然卫星截止高度角增加，但是组合系统卫星的数量依然是单系统的两倍，因此仍然能够成功地解算出测站坐标。另外，卫星截止高度角的增加，会使得PDOP值急剧上升，但是组合系统的PDOP值仍然小于单系统的值。从图3中可以看出，即使高度角增大组合系统的定位精度和稳定率都要高于单系统。

2.2 北斗+GPS在亚太地区的性能分析

由于北斗卫星导航系统正在建设当中，全球组网刚刚开始，为了全面评价北斗及北斗+GPS组合定位的性能，选用亚太地区及其周边的一些能够同时接收北斗与GPS信号的MGEX网中的测站来全面地评价其性能。

表2是12个测站3种计算方法在E、N、U方向的平均误差、卫星的平均个数及PDOP的平均值。

表2 12个测站东北天(E、N、U)方向的平均均方根误差、卫星个数及PDOP值

参数BDSGPSBDS/GPS 提高率(%)E/m6.18321.33261.093982.3/17.9N/m4.16871.99851.343367.8/32.8U/m13.09154.28103.922569.5/6.7平均卫星数6.11168.845214.5276137.7/64.24PDOP6.09071.95651.458776.1/25.4

由图4可以看出，所选的12个测站北斗导航系统的定位精度很不稳定，有几个测站(如cas1、kzn2、samo、zim3)精度较差，这与测站所处的地理位置有关。这几个测站都处在欧洲地区或亚太地区附近，导致所接收到的北斗卫星的个数较少，观测值较少，从而精度降低。从这12个测站的定位情况中可以看出，GPS的位置精度和稳定性都要高于北斗，组合单点定位的精度最高。北斗+GPS组合定位精度相对于北斗的提高幅度要远大于相对于GPS的提高幅度。说明我国北斗系统之中仍然存在许多误差项需要不断的优化[17]。

3 结 论

我国北斗卫星导航系统已经进入了全球组网的阶段，正在如火如荼的建设当中，本文利用实测数据，通过方案设计可以得到如下结论：

图4 12个测站的东北天(ENU)方向均方根误差、平均卫星个数及POP值

(1) 北斗+GPS组合单点定位在E、N、U 3个方向的精度和稳定性均优于北斗和GPS单系统。

(2) 北斗+GPS组合系统的卫星个数是单系统卫星个数的两倍，组合系统的PDOP值远小于单系统的PODP值。组合系统在卫星截止高度角增加的情况下，优势明显，定位精度和稳定性优于单系统。尤其是在卫星截止高度角较高的情况下，远优于单系统的定位精度和稳定性。

(3) 虽然北斗在亚太地区已经能够提供定位服务，但是北斗单系统定位的精度和稳定性均低于GPS单系统定位的精度。说明北斗系统中还有很多地方需要完善。

随着北斗卫星星座的逐步完善，相信北斗单系统和北斗+GPS组合单点定位的精度都会有所提高。如何利用全球多个系统进行组合单点定位，以及利用多个系统进行精密单点定位将成为下一步研究的重点。

[1] 黄丽霞. GPS、北斗卫星导航系统组合单点定位模型及算法[J]. 电子科技, 2014, 27(7):23-25.

[2] 安向东. GPS 与北斗伪距单点定位性能对比分析[J]. 全球定位系统, 2014(3):8-14.

[3] 陆亚峰, 楼立志, 马绪瀛,等. 北斗与GPS组合伪距单点定位精度分析[J]. 全球定位系统, 2013(6):1-6.

[4] 李彬, 李征航, 刘万科. COMPASS/GPS/GLONASS系统组合在中国区域的仿真分析[J]. 大地测量与地球动力学, 2013, 33(6):94-97.

[5] 龙昌生. 北斗/GPS双模导航终端关键模块的设计与实现[D]. 重庆：重庆大学, 2011.

[6] 陈杨毅. GPS与BD双模GNSS接收机定位解算技术研究[D]. 厦门：厦门大学, 2014.

[7] AGENCY M. United States Department of Defense, World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems[R]. [S.l.]: NIMA, 2000.

[8] SEGUY J. Maintenance and Enhancement of the World Geodetic System 1984[J]. Proceedings of ION GPS-94, 1994(37):244-245.

[9] ABUSALI P A M, SCHUTZ B E, TAPLEY B D, et al. Transformation between SLR/VLBI and WGS-84 Reference Frames[J]. Journal of Geodesy, 1995, 69(2):61-72.

[10] BURWELL R M. Magellan Announces the GPS Companion for the Handspring Visor[J]. Critique Studies in Contemporary Fiction, 2013, 15(1):48-58.

[11] KAI B, DENNIS A A. A Software Defined GPS and Galileo Receiver[M]. Boston: Birkhäuser, 2007.

[12] CHANGSHENG C. A Combined GPS/GLONASS Navigation Algorithm for Use with Limited Satellite Visibility[J]. Journal of Navigation, 2009, 62(4):671-685.

[13] BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines Up to 2000 km[J]. Journal of Geophysical Research (Solid Earth), 1989, 94(B8):10187-10203.

[14] PAN L, CAI C, SANTERRE R, et al. Performance Evaluation of Single-frequency Point Positioning with GPS, GLONASS, BeiDou and Galileo[J]. Survey Review, 2016:1-9.

[15] 高星伟, 过静珺, 程鹏飞,等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012,41(5):743-748.

Accuracy Evaluation and Analysis of Single Point Positioning with BeiDou and GPS

WEI Erhu1,LIU Xuexi1,LIU Jingnan2

(1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;2. GNSS Research Center, Wuhan University, Wuhan 430079, China)

BeiDou Navigation Satellite System(BDS) has now entered the stage of global networking. In this paper, the mathematical model of BDS/GPS single point positioning is derived in detail. Two schemes are designed by using the data of one single station or twelve stations in the Asia Pacific Region of the MGEX to evaluate and analyse the accuracy of single point positioning with BeiDou and GPS. The mathematical model of single point positioning is verified by experiments. The results show that the accuracy and stability of the combined single point positioning are better than the single system. This paper aims to provide reference for the popularization and application of BeiDou system.

BeiDou; GPS; single point positioning; combined system; accuracy evaluation

魏二虎，刘学习，刘经南.北斗+GPS组合单点定位精度评价与分析[J].测绘通报，2017(5)：1-5.

10.13474/j.cnki.11-2246.2017.0142.

2016-10-08

国家自然科学基金(41374012)

魏二虎(1965—)，男，博士，教授，主要研究方向为空间大地测量与地球动力学。E-mail:ehwei@sgg.whu.edu.cn

P228

A

0494-0911(2017)05-0001-05