波流与不均匀海域上浮式弹性板相互作用的非线性数值模拟
2017-06-19嵇春艳翟钢军
程 勇,嵇春艳,翟钢军
(1. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003; 2. 大连理工大学 深海研究中心,辽宁 大连 116024)
波流与不均匀海域上浮式弹性板相互作用的非线性数值模拟
程 勇1,嵇春艳1,翟钢军2
(1. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003; 2. 大连理工大学 深海研究中心,辽宁 大连 116024)
波流混合作用下浮式弹性板的水弹性响应属于非线性范畴,尤其当波流传递到不均匀海底时,这种非线性行为更为复杂,因而采用完全非线性分析技术是唯一可能获得浮板精确水弹性响应的方法。采用高阶边界元法建立模拟波流与变水深海底上浮板相互作用的时域完全非线性二维数值水槽;将Euler-Bernoulli-von Karman非线性梁模型加入到流固交界面的动力学边界条件中实现波流与浮板耦合作用,运用4阶Runge-Kutta法并联合混合欧拉-拉格朗日方案对瞬时自由水面和流固交界面进行更新;为获得浮板位移的空间各阶导数,使用一系列模态振型函数来近似当前时刻浮板的垂向位移,并利用Galerkin 方法求解各阶模态主坐标。通过与无网格数值已知算法结果进行比较,验证了数值模型的可行性和准确性;进一步研究水流及不均匀海底的存在对浮板非线性水弹性响应产生的影响;最后探讨了不同流速对浮板高阶谐位移的影响规律。
浮式弹性板;高阶边界元方法;时域完全非线性;水弹性响应;波流混合作用;不匀均海底
超大型浮式结构物(Very large Floating Structure,VLFS)是利用海洋空间和开发海洋资源的一种新型海洋结构物,也是解决沿海城市人口增多、空间缩小和资源匮乏的最有效途径。目前,超大型浮式结构物已应用于海上石油储备、海上机场、漂浮轮渡、废水处理厂和军事中转站等建设。
超大型浮式结构物,尤其是厢式超大型浮体,其水平尺度远大于垂向尺度,并且弯曲刚度比较小,使得结构在波浪作用下的弹性变形可能与刚体位移同一量级,甚至更高[1]。因此,许多学者将其假定为一有限厚度的弹性薄板,进行水弹性响应分析。Wu等[2-6]采用频域解析或数值方法快速、简单、有效地预报了稳定波态下的水弹性振幅响应算子。然而,当考虑非线性因素和瞬态响应时,超大型浮体的水弹性响应必须采用时域方法求解。传统的水弹性响应时域求解方法包括直接时域法和间接时域法,前者将水波边界积分方程和结构运动方程直接在时域里离散并求解,而后者通过傅里叶变换将频域里的水动力系数转换为时域内的迟滞函数、附加质量和波浪力,通过脉冲运动的叠加建立时域方程进行求解。这些时域理论的数值方法包括边界元法(Boundary Element Method, BEM)、有限元法(Finite Element Method, FEM)、有限元-边界元混合方法(Hybrid Finite Element-Boundary Element Method, FE-BE)。Watanabe等[7-9]采用有限元法对VLFS在额外动力载荷如重物坠落、飞机起飞和着陆等作用下的瞬态响应进行了分析,虽然模型比较简单,但对于研究时间历程的响应分析,计算相当耗时;Kashiwagi[10-11]基于间接时域模态展开方案采用边界元法计算了浮式机场的瞬态响应,其中引入记忆项来处理流场的水动力系数的卷积,且高频时进行截断处理,从而较好地解决了忽略记忆项一段时间以后带来的计算误差问题;Endo[12]采用有限元-边界元混合方法分析了一厢式VLFS在波浪和飞机起飞或着落同时作用下瞬态响应;Cheng等[13]采用满足自由水面的时域格林函数方法对VLFS迎浪端和尾端水下一定位置处配置水平减振板时波浪作用下的水弹性响应进行了数值和试验研究,并对水平透空、不透以及透空-不透空组合减振板的减振效率进行了系统的分析。
上述文献主要研究了VLFS的线性水弹性时域理论,虽然简单,但由于忽略了非线性影响,对大振幅波浪引起的结构大幅运动计算结果往往会产生较大误差。陈徐均等[14-15]建立了浮体二阶水弹性力学方程,分别讨论了流体非线性和结构非线性对浮体水弹性响应的影响;Liu等[16]引入自由水面的非线性条件并采用有限元-边界元混合方法计算了一弹性浮板分别在规则波、不规则波以及孤立波浪作用下的水弹性响应;Kyoung等[17]采用有限元法计算了完全非线性波浪与超大型浮体的水弹性响应;Mollazadeh等[18]和Mirafzali等[19]分别借助高斯基函数和多节点B样条基函数近似自由水面和流固交界面的垂向位移,采用无网格粒子法计算了完全非线性波浪分别与一半无限、有限板的水弹性相互作用。然而,这些研究都只关注了纯波浪与弹性浮体之间的非线性相互作用,而现实中的VLFS常安置在近海区域,近海水域存在的波浪传播经常受到水流的影响,例如:顺流时波高减小,波长增大;逆流时波高增加,波长减小等[20]。因此,研究均匀水流中波浪与浮式弹性板的水弹性相互作用更加符合实际情况。另一方面,目前对VLFS的非线性水弹性响应研究几乎都是建立在常水深的均匀海洋环境基础上,但近海区域的海底自然变化形成的浅礁和暗礁会对波浪发生反射和透射效应,同时由于海底的浅水效应将产生高阶谐波,改变波浪的波高和能量谱分布,从而进一步对浮式弹性板的水弹性响应产生影响。针对波流相互作用和不匀均海底环境影响这两个方面,本文采用高阶边界元方法,建立时域二维完全非线性数值水槽模型来模拟水流影响下波浪与不均匀海域上浮式弹性板的水弹性互相作用。其中,由控制垂直源造波线产生指定入射波浪,水槽两端采用人工阻尼层防止水槽尾端的反射和入射边界的二次反射,对瞬时自由水面条件利用混合欧拉-拉格朗日方法进行追踪,并采用4阶Runge-Kutta法更新下一时间步的自由水面高程和速度势。基于模态展开法,利用一系列满足自由边界条件的振型函数叠加表达式近似浮板与水面交界面的垂直位移,并采用Galerkin法求解每个时间相应的模态幅值,这与Mollazadeh等和Mirafzali等径向基函数法相比,减少了线性方程组未知数个数(等于模态幅值个数)。为了避免由于自由水面质点运动而引起的数值不稳定问题,对每一时刻的网格进行重新划分。最后,进一步分析了水流的方向以及不均匀海底的存在等对总体水弹性响应及各高阶响应成分的影响规律。
1 数学模型
1.1 流场控制方程和边界条件
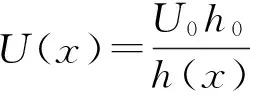
2φ=2φ=0
(1)
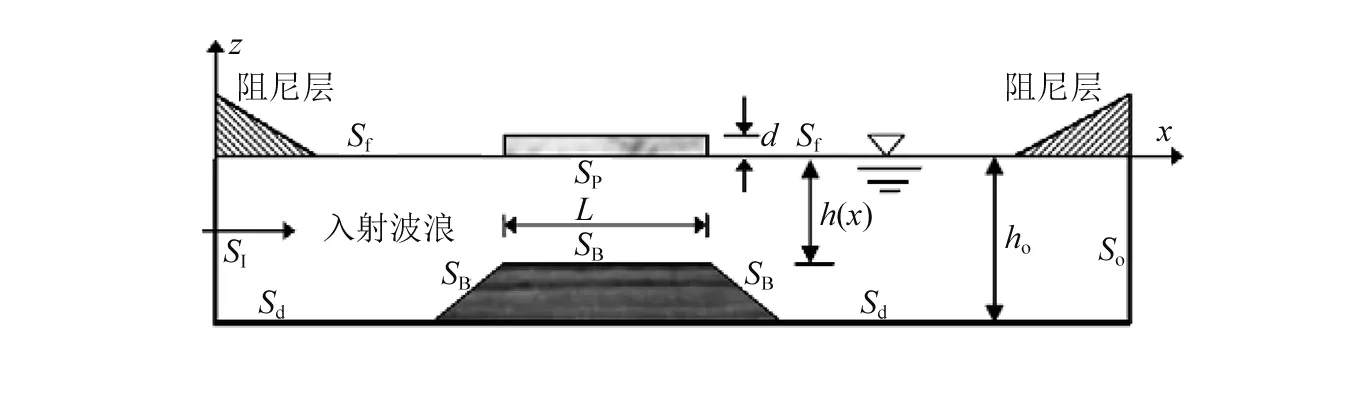
图1 二维数值波流水槽示意图Fig.1 Schematic diagram of a 2D numerical wave-current tank
在瞬时自由水面,完全非线性运动学和动力学边界条件由物质导数和伯努利方程表达式推导而来。本文采用混合欧拉-拉格朗日方法追踪每一时刻自由水面的流体质点,更新水面可分两步:①在欧拉框架下求解上述Laplace方程;②运用拉格朗日法来更新边界上的节点坐标及相应物理量值。在水槽的两端布置阻尼层1和阻尼层2来分别吸收从物体反射回来和透射过去波浪。进一步假定浮式弹性板和自由水面的交界面处的流体质点在波浪与结构物相互作用的过程中始终与浮板底面不发生分离,则与自由水面动力学边界条件相比,流固交界面压力不再等于大气压强,而自由水面条件相似。这样,拉格朗日系统下,自由水面和流固交界面处的边界条件可写为:
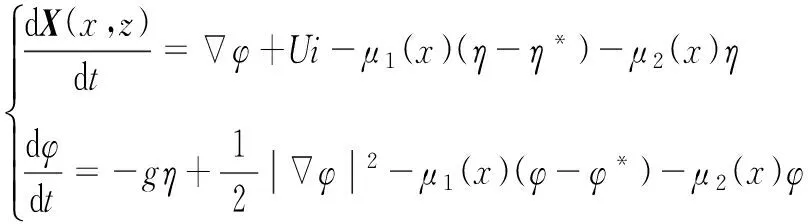
(2)

(3)
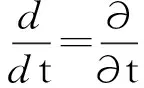
(4)
式中:x1和x2分别为阻尼层1和阻尼层2的起始位置;Lb为阻尼层的有效长度;本文取入射波长的1.5倍;ω为基频波的角频率。
浮式弹性板的水弹性响应与流体运动即速度势是相互耦合的,即浮式弹性板底面的流体压力通过自由面动力学边界条件式(3)改变结构的运动状态,而结构运动状态反过来又影响结构底面的流体压力。这样,基于Euler-Bernoulli-von Karman非线性梁理论[21]可得交界面压力和垂向位移之间的关系表达式:
(5)
式中:EI=Ed3/[12(1-v2)]是浮板的垂向弯曲刚度;E、v和d是浮板的弹性模量、泊松比和厚度;EA是轴向刚度;ms是单位面积的质量。
在水槽底部和侧壁满足固定不透水边界条件:
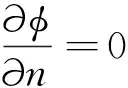
(6)
在水槽入射边界条件,给定水质点沿垂直断面的理论速度分布值:
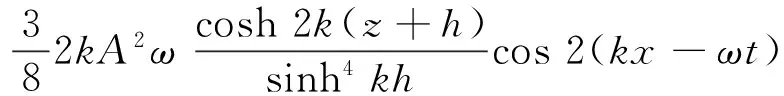
(7)
式中:A和k分别为入射波浪波幅和波数。考虑到流的存在,波数k与角频率ω满足如下色散方程
(ω-kU)2=gktanhkh
(8)
为了在时域里求解以上边界值问题,以下初始条件需满足:
(9)
1.2 数值求解方法
在整个计算域运用格林第二公式,则以上边界值问题可转化为如下边界积分方程:
(10)
式中:p和q分别为源点和场点坐标;α为固角系数;G为关于水底镜像的格林函数;可表达为如下形式
(11)
通过二次型函数将边界离散为三节点曲线单元,单元内任意一点的物理量包括几何坐标,速度势和速度势法向导数可以由二次型函数插值得到:
(12)
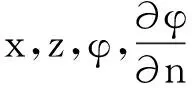
通过数学变换,将节点笛卡尔坐标转化为等参高斯坐标,每个单元内布置4个高斯点。这样,式(10)可离散为如下形式
(13)
式中:Jj为雅可比行列式;Ne1为自由水面和浮板底面的离散单元数;Ne2为入射边界、出流边界和不均匀海底表面的离散单元数。经过一系列的推导,可将式(13)简化为以物面速度势和自由面速度势法向导数为未知数的线性方程组形式,由于积分边界每一时刻都在变化,因此当前时间步的系数矩阵和向量需重新建立再求解。
由式(13)计算获得物面速度势和自由面速度势后,采用4阶Runge-Kutta法由自由水面和流固交界面边界条件式(2)和式(3)计算下一时刻的水质点位置和速度势。这里,式(2)和式(3)中的速度势的Laplace算子可由下式计算
(14)
式中:上标(t)表示当前时刻。
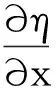
(15)
式中:fj(x)和ζj分别为第j个模态的振型函数和相应的模态幅值。
为了保证数值模拟的收敛性,选择适当的模态函数非常关键。采用Newman[22]推导的满足自由边界的梁振动的自然模态,有很多学者验证了它的表达式和其收敛性
(16)
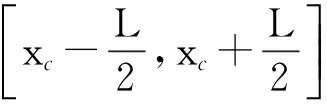
对式(15),应用Galerkin积分方法,即方程两端同时乘以模态函数,并沿流固交界面积分,可得以下线性组方程:
[Aij]{ζj(t)}={Bj}i,j=1,…,M
(18)
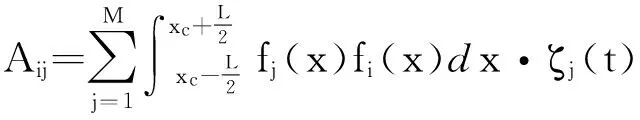
当前时刻的浮板位移已知时,通过求解上述线性方程组可得各模态幅值大小,紧接着可求出位移的各阶导数
(19)
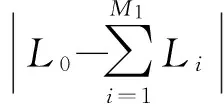
1.3 计算流程
针对以上数学公式及求解方法,本文采用Fortran语言进行程序开发,求解出不均匀水域里浮式弹性板在波流耦合作用下的水弹性。总的计算流程,如图2所示。主要包括以下阶段:
(1) 获得自由水面、流固交界面、入射边界、出流边界和不匀均海底离散单元上的各节点初始时刻的空间坐标、节点编号和单元编号,并假定初始时刻的速度势和波面高程为0;
(2) 采用HOBEM求解式(10),获得当前时刻物面上的速度势和自由面上的速度势法向导数;

(4) 基于模态展开法,采用一系列模态函数插值浮板位移,并应用Gaelerkin法获得各阶模态幅值大小,根据式(19)计算板位移的各阶空间导数;
(5) 采用4阶Runge-Kutta法根据完全非线性自由水面和流固交界面条件式(2)和式(3)更新下一时刻的自由面位置和速度势;
(6) 利用二次形函数在旧单元里的插值获得新节点的物理量使自由水面和流固交界面网格重新划分,并重新求解积分方程获得下一时刻物面速度势和自由面速度势的法向导数;
(7) 至此,程序正式进入循环计算阶段,直到最终预定的时间结束。

图2 数值计算流程图Fig.2 Algorithm for numerical simulation
2 数值结果分析
2.1 程序的验证
为了验证本文数值方法及程序的可行性,选用Mollazadeh等和Mirafzali等的半无限板和有限板数值模型作为算例,并将本文模型计算结果与他们的无网格法计算结果进行比较。这里,首先考虑均匀海底即水深为h=0.38m的常水深情况,半无限板和无限板板长分别为20m和5m,厚度均为0.01m,杨氏弹性模量E=106N/m2,板密度为ρs=100kg/m3,板放置在水槽的工作区域,迎浪端距造波端的距离为20m。如果本文的控制方程中不考虑水流的作用,则数值模型可模拟相同条件下的纯波浪情况,波浪周期和波幅分别为T=2.75s和A=0.028 3m。
经过开展数值收敛试验选定时间步长为△t=T/60,共模拟30个周期,半无限板时的水槽长度为10λ,有限板时的水槽长度为8λ,这里λ为波长。水槽长度和垂直方向分别布置200和4个单元。水槽两端的阻尼层长度为1.5λ。
图3给出了指定位置x=20m(无限板的迎浪端)和x=28m(无限板内部)的水弹性响应时间历程曲线即本文边界元结果、Mollazadeh等和Mirafzali等无网格法结果的比较。其中,Mollazadeh等采用高斯基函数近似板位移而Mirafzali等采用多节点B样条基函数插值板位移。从总体上看,三种数值方法的数值解彼此吻合的较好,都能准确地模拟浮式弹性板在波浪作用下的水弹性响应过程。然而,在板的迎浪端,本文的位移曲线比Mollazadeh等和Mirafzali等的结果更加光滑,说明了本文模态函数插值板的位移不仅能减少未知数个数(等于模态函数个数),提高计算效率,而且当浮板具有一定厚度时,在板边缘与自由水面交点处还能表现更好的数值稳定性能。

(a) x=20 m
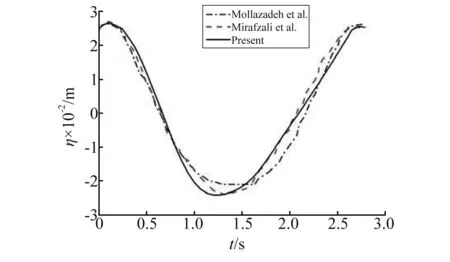
(b) x=28 m图3 x=20 m和x=28 m处浮板位移的时间历程Fig.3 Time series of plate displacement at x=20 m and x=28 m
图4是t=21.8s时波面和无限板底面沿水槽的分布。由图4可知,本文数值结果和以上两文献结果在水槽的有效长度内(x<40m)吻合良好,进一步验证了本文数值方法的准确性。水槽尾端数值结果偏差的原因是,本文的数值水槽尾端采用1.5λ长度的有效阻尼层吸收来波,而Mollazadeh等和Mirafzali等在水槽出流边界上采用的是波浪向外传播的Sommerfeld-Orlanski辐射边界条件,对于时域内的完全非线性水动力问题,辐射条件中的波相速度其实是很难准确确定。与无限板类似,图5描述了t=23s时自由水面和有限板位移的沿程分布情况。由图5可知,除了水槽尾端的数值差别,本文数值模型计算结果与无网格结果满足良好的一致性。
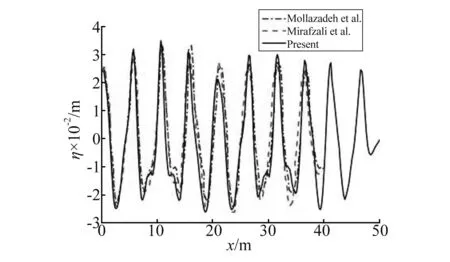
图4 t=21.8 s时自由水面和无限板底面位移沿水槽分布情况Fig.4 Wave and semi-infinite plate profiles along the wave tank at t=21.8 s
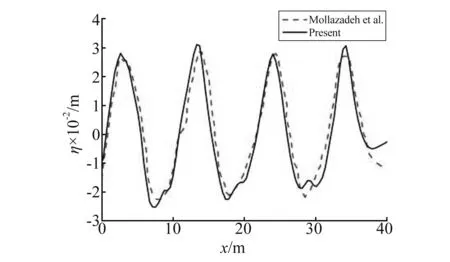
图5 t=23 s时自由水面和有限板底面位移 沿水槽分布情况Fig.5 Wave and finite plate profiles along the wave tank at t=23 s
2.2 水流的影响
接下来考虑水槽中均匀海底时,波流同向、反向联合作用情况,这里取水流速度U0=0.25m/s,浮板取“2.1”相同参数的有限弹性板,水槽和波浪参数也如“2.1”所述。
图6(a)~图6(c)分别是浮板迎浪端、中间位置和尾端在逆流、纯波浪和顺流工况下的垂向位移比较结果。由6图可知,浮板各位置都经历一定的缓冲时间达到相对稳定状态,由于本文模型属于浅水条件,各水质点之间存在一定的能量交换,以至于随着波浪沿板长度方向传播,板的迎浪端、中间位置和尾端之间的稳定波幅并不相同;波流同向与纯波浪比较各位置水弹性响应具有超前性,而波流反向与纯波浪比较水弹性响应具有滞后性,这是因为由色散方程式(8)可知,波流同向时波数最小,波浪传递速度最大,而波流反向时则相反;三种工况下为垂向位移比较显示波流同向时波峰值最小,波谷最陡,甚至在浮板出现二阶波谷,而波流反向时波峰最大,波谷最平坦。
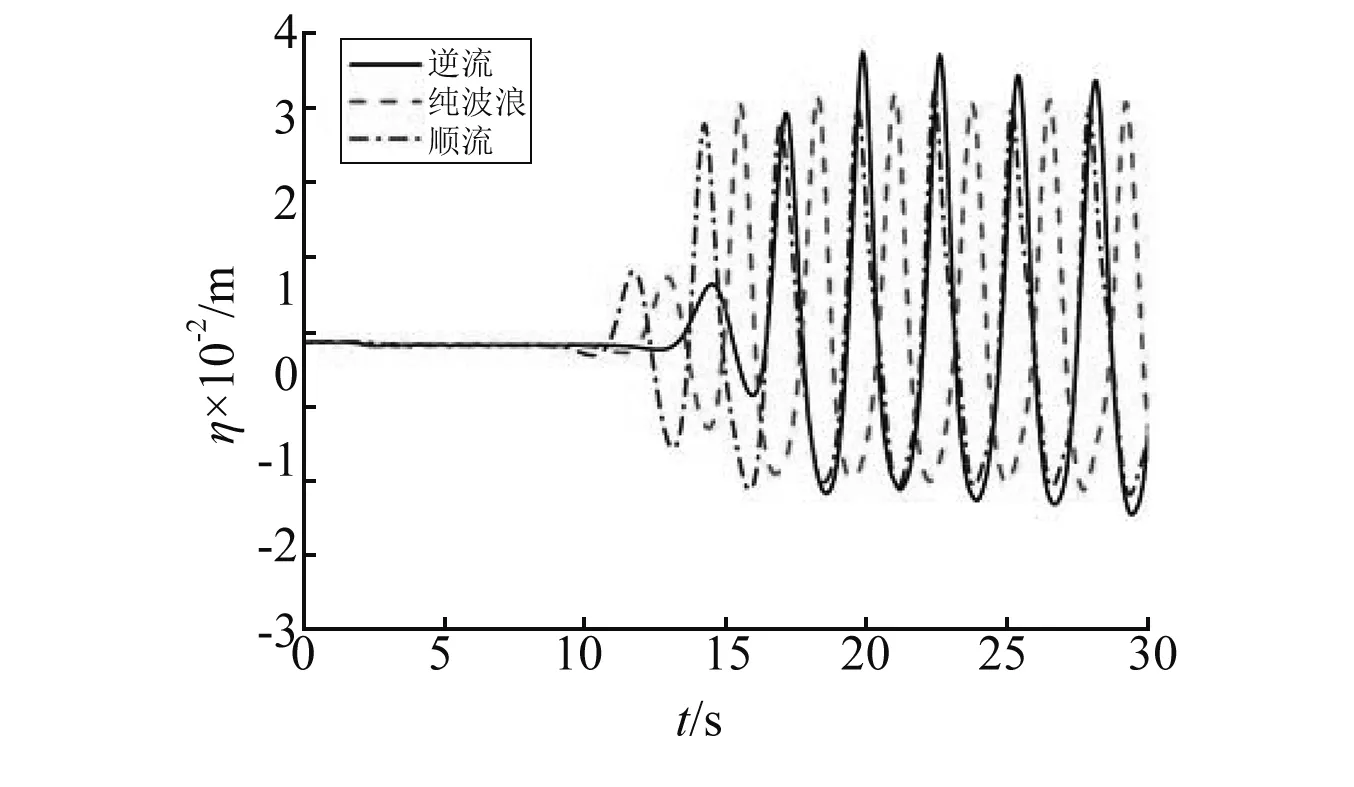
(a) 迎浪端
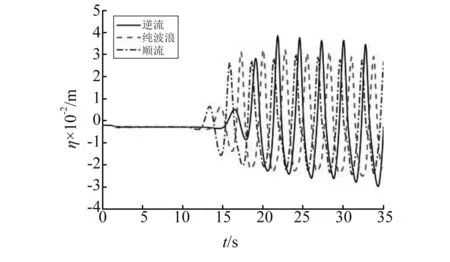
(b) 中间位置
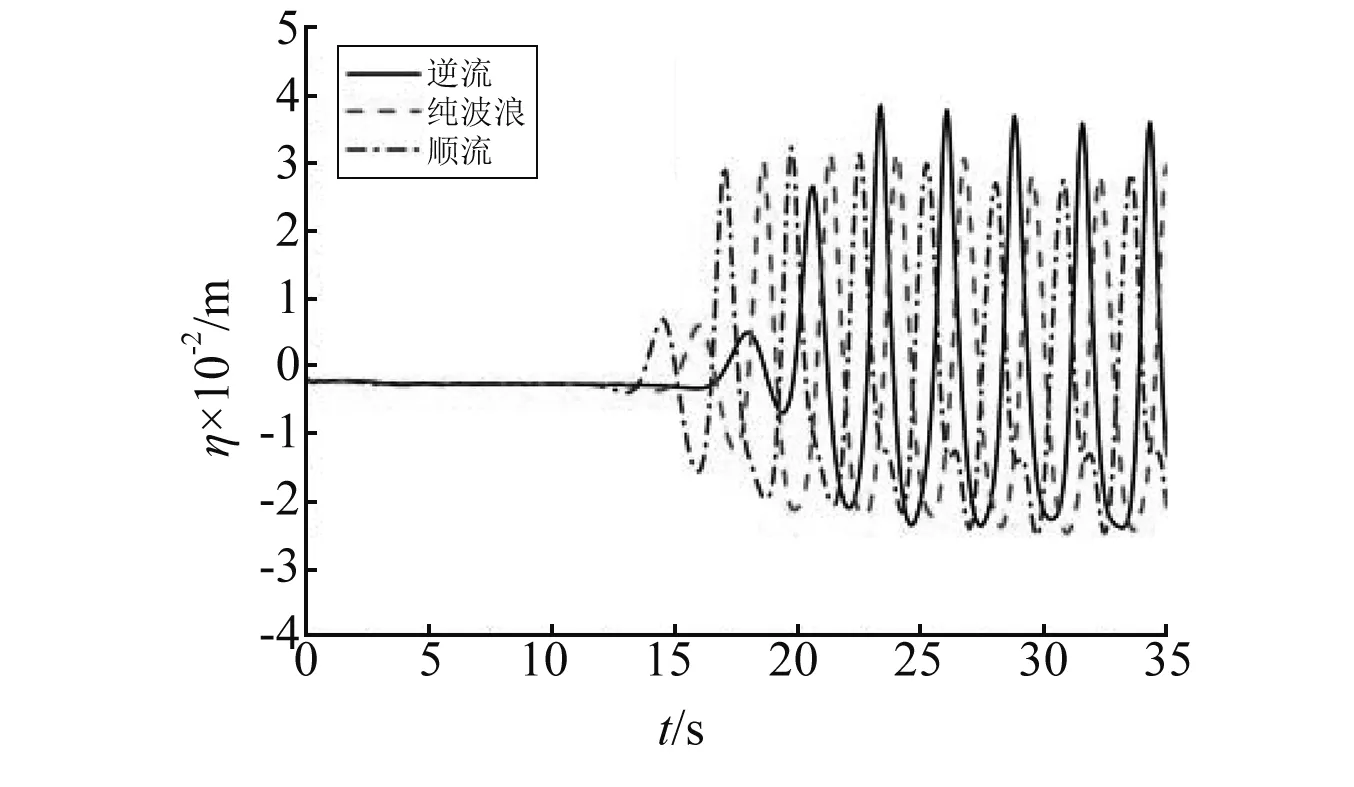
(c) 尾端图6 不同流速时浮板迎浪端、中间位置和尾端的垂向位移历程Fig.6 Time series of vertical displacement of the plate for different currents
针对图6中浮板不同位置处的垂向位移进行傅里叶变换得到相应的频谱关系,如图7所示。由图7可知,海流的出现使浮板位移出现更多二阶和三阶高频成分,浮板位移的非线性特性增强,尤其对于逆流情况;总体上,逆流增加了浮板的波频响应,而顺流情况则相反。
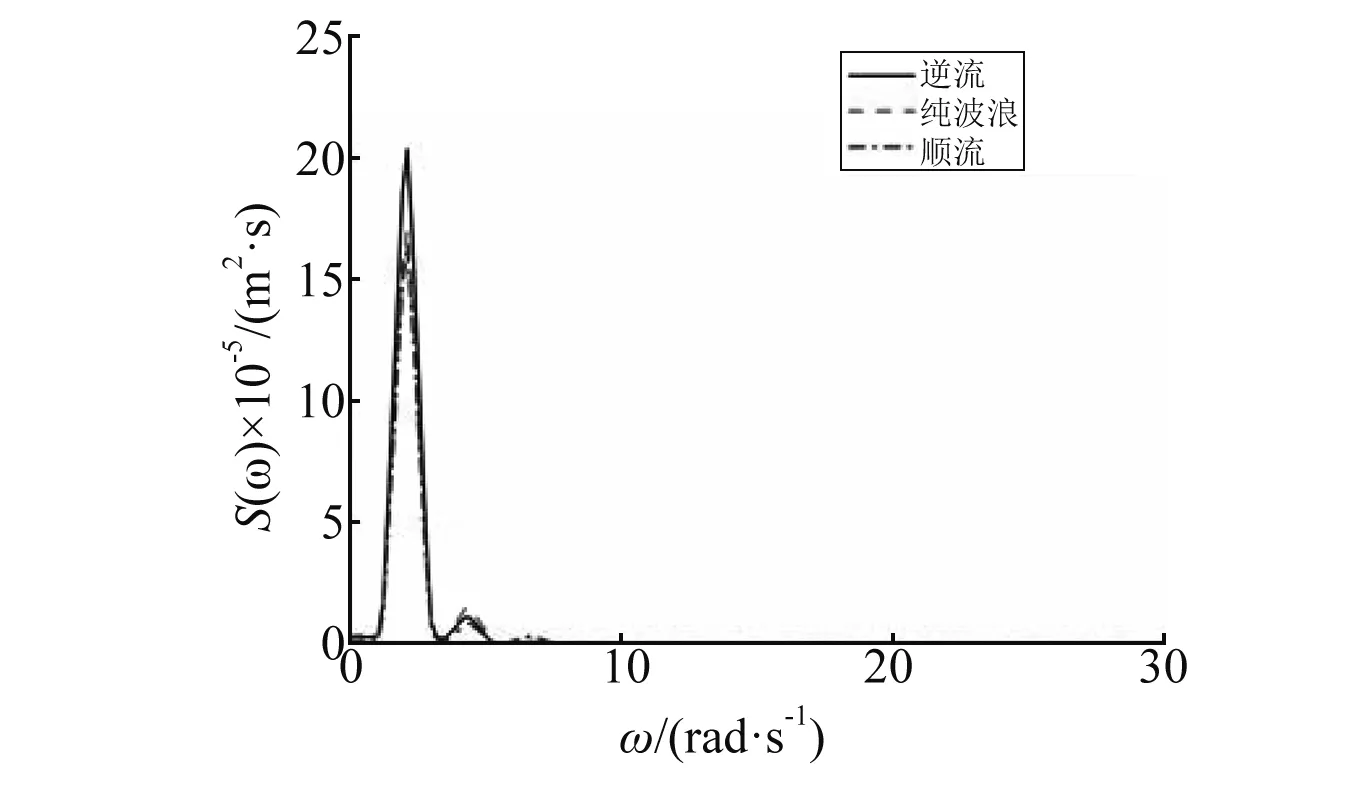
(a) 迎浪端
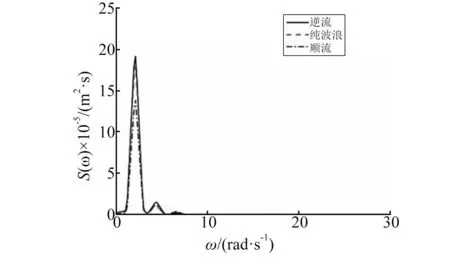
(b) 中间位置
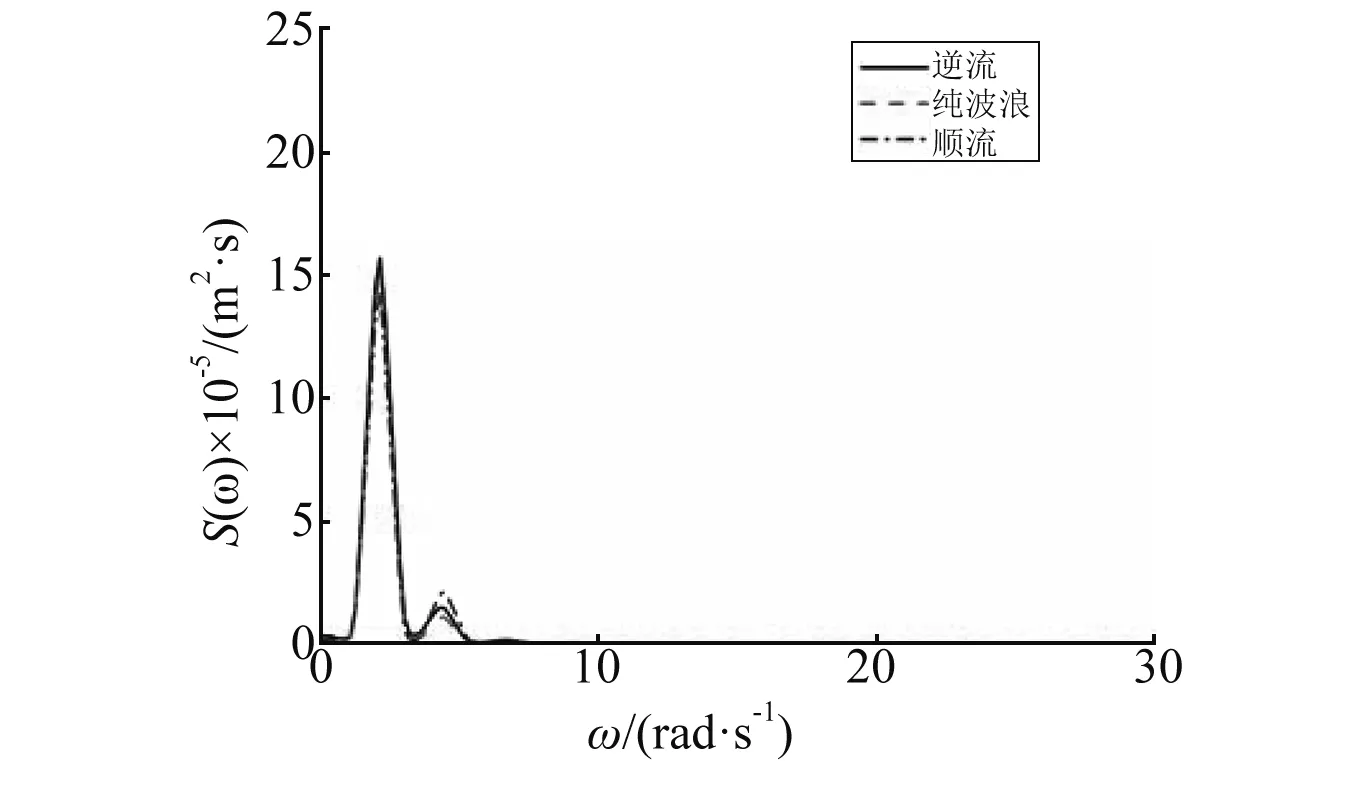
(c) 尾端图7 不同流速时浮板各位置在均匀海域中的垂向位移响应谱Fig.7 Hydroelastic response spectra of the plate over flat sea-bottom for different currents
图8是t=20T和22T时波流逆向、纯波浪和波流同向三种工况下自由水面和流固交界面高程沿水槽长度的分布情况。从图8可知,三种工况下20T和22T的自由面高程已经完全吻合,说明当时间达到20T时,波流沿水槽传播已稳定,本文数值计算已达到收敛,对纯波浪和波流混合作用都可以取得理想的数值结果;水槽尾端的阻尼层区域中,波浪能量慢慢地被吸收,表明阻尼层的消浪效果良好;波流逆向时波面和浮板位移最大,波流同向时位移最小;由波流逆向到纯波浪再到波流同向,自由水面和流固交界面的双谷现象越来越明显,这说明了顺流工况下二阶作用越来越突出,倍频位移成分在总体位移中所占比例最大。
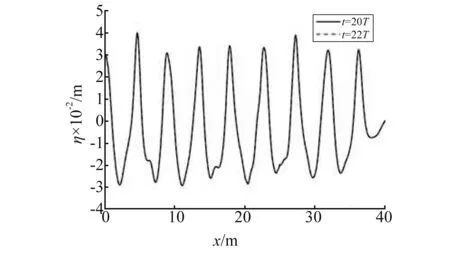
(a) U0=-0.25 m/s

(b) U0=0 m/s
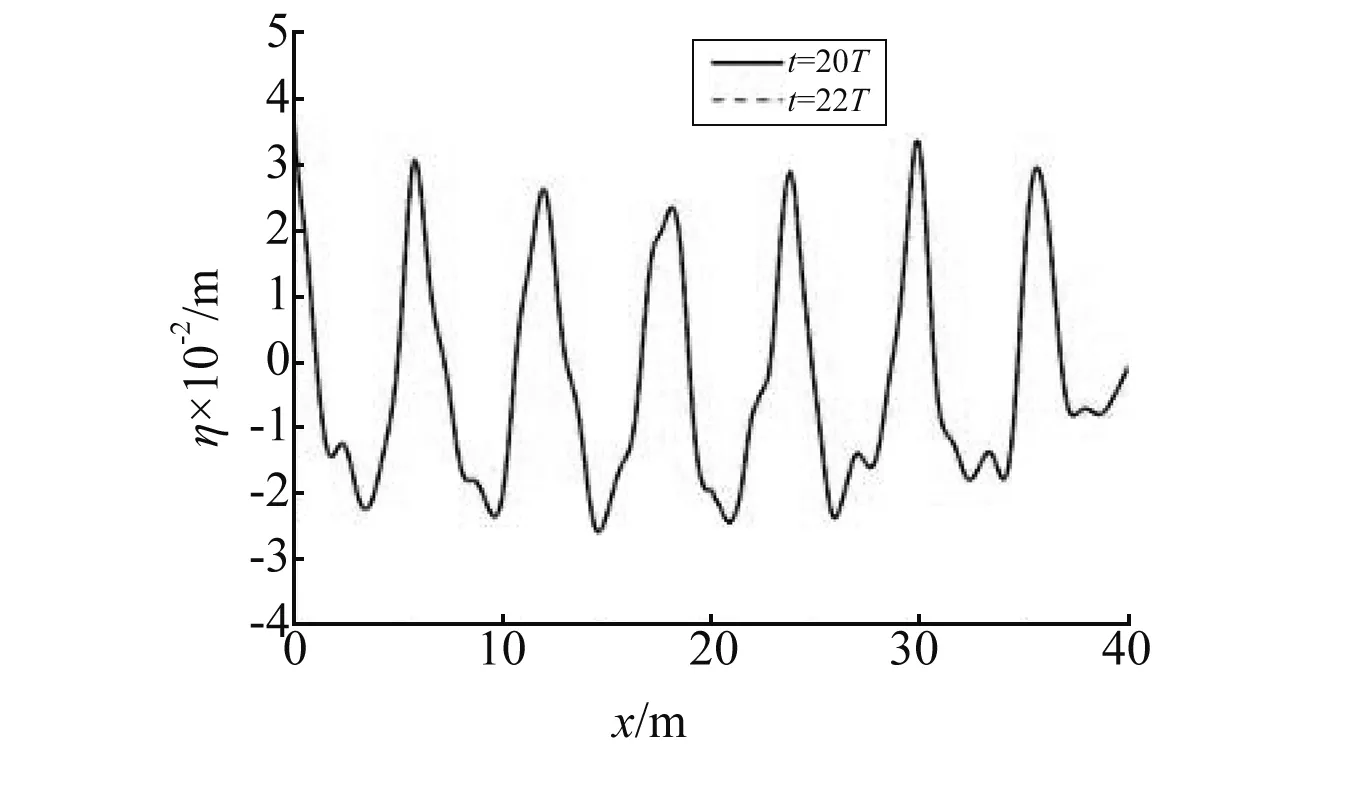
(c) U0=0.25 m/s图8 t=20T和22T时自由水面和流固交界面 的垂向位移沿水槽分布图Fig.8 Surface elevation along the wave tank at t=20T and 22T
2.3 不均匀海底的影响
我国南海海域蕴藏着丰富的岛礁,而这些岛礁周围的建设目前仍十分落后,因此选择地理位置、区域环境较为关键的岛礁,建立岛礁上的VLFS来开发海洋资源和利用海洋空间,具有重要的战略意义。为此,本节在浮式弹性板正下方布置梯形断面形式的海底,考虑水槽中布置不均匀海底时波流混合作用下的浮板总体水弹性响应和高阶谐位移。水槽尺寸、浮板的几何参数以及入射波浪参数与“2.1”所述相同,海底地形尺寸,迎浪侧和背浪侧坡度,如图9所示。不均匀海底迎浪侧表面网格尺寸为△x=P1/20,底部网格尺寸为△x=P2/25,背浪侧网格尺寸为△x=P3/10,这里P1,P2和P3分别表示海底迎浪侧,顶部和背浪侧长度,其他网格尺寸和时间步长同以上算例。
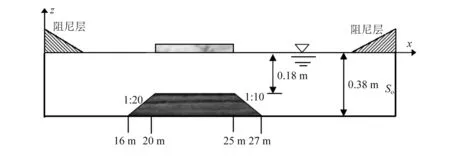
图9 不均匀海底地形的布置Fig.9 Definition sketch of the variable depth sea-bottom
图10是浮板迎浪端、中间位置和尾端在不同流速时的非线性垂向位移时间历程比较。对比同一图中的三种不同流速工况下的垂向位移可发现,逆流时位移峰值最大,且位移波谷处存在很多高频分成,而顺流时位移峰值最小,且波谷曲线很光滑,不存在高频部分,这表明逆流会增加浮板水弹性响应的非线性,而顺流则减弱波浪的非线性。逆流情况下,垂向位移从浮板迎浪端到中间位置再到尾端是逐渐降低的,纯波浪时位移是先降低后增加,而顺流情况下位移是逐渐增加的。对比均匀海底的数值结果(见图6)可得到,不均匀海底的存在不仅增加的浮板的垂向位移值,而且由于浅水效应,使得位移曲线更加陡峭,即非线性增强。因此,针对近海不均匀海域上大型浮式结构物在波流混合作用下的水弹性响应分析,采用本文的完全非线性数值模型是合适的。
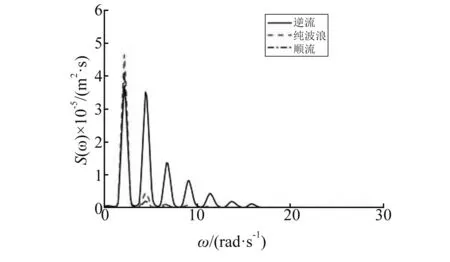
图11(a)~图11(c)给出了图10中迎浪端、中间位置和尾端的垂向位移频谱关系。从图11可知,不均匀海底中水流的存在是浮板水弹性变化的重要原因之一,而这种非线性相互作用尤其对于逆流时会导致高频和低频能量的产生,从而使得浮板各个位置的响应频谱亦不一致;顺流时浮板的波频响应大于逆流的波频响应,而逆流时浮板会产生更多的高阶谐响应,这种非线性差异在浮板迎浪端即不均匀海底迎浪侧端点最明显,到浮板尾端即不均匀海底背浪侧端点更高阶非线性差异(如三阶、四阶、五阶谐位移)逐渐减小,而低频能量差异逐渐增加;浮板的波频位移成分从迎浪端到尾端在三种水流情况中均逐渐减小,而高阶谐位移从迎浪端到尾端在逆流中逐渐减小,在无流和顺流中逐渐增加,另外,在逆流中浮板中间和尾端的低频垂向位移逐渐突出;对比均匀海底时浮板垂向位移的频谱关系(图7),可发现不均匀海底使位移出现了更多高阶成分,明显地增加了位移的非线性特征。

(a) 迎浪端
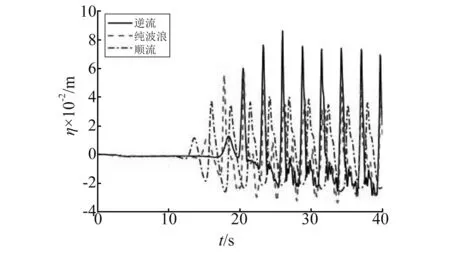
(b) 中间位置
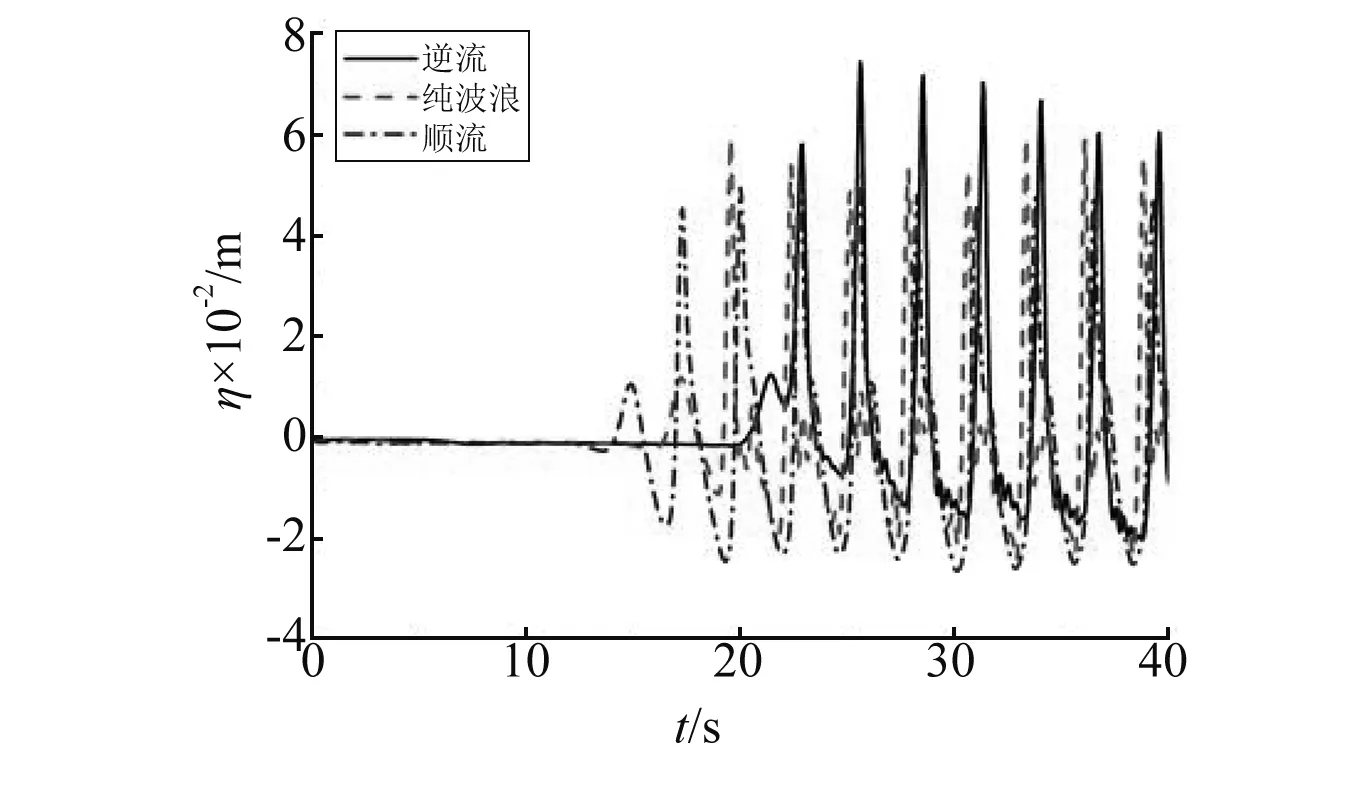
(c) 尾端图10 梯形断面形式海底上方浮板的迎浪端、中间位置和 尾端在不同流速时的垂向位移比较Fig.0 Time-history comparisons of vertical displacement of the plate placed over the trapezoid-shaped sea-bottom among opposing, without and following currents
最后,将基于上述梯形断面形式的不匀均海域上弹性浮板在波浪和不同流速均匀流混合作用下的水弹性计算结果进行对比分析。图12显示了浮板迎浪端、中间位置和尾端的前三阶垂向位移响应谱的标准差(STD)随均匀流速的变化。值得一提的是,我们分别将频率范围0.81 ~3.32rad/s,3.32 ~5.57rad/s和5.57 ~7.98rad/s定义为波频、二阶和三阶区域。从总体的计算结果来看,随着流速从逆向到正向的增加,基频位移响应谱的标准差有一定程度的增加,而二阶和三阶位移谱的标准差逐渐减小。这是因为随着流速的增加,由色散关系可知波长也会随之增加,导致非线性因子波陡2A/λ会相应的减小,从而减弱水弹性响应的非线性;均匀流流速0值附近,各阶垂向位移趋势会有突变,说明浮板水弹性响应在不均匀海底中对低流速也比较敏感,这可能是因为本文算例中的堤上比较浅,水流经过潜堤堤顶时,水体流量不变,则此时水流流速增幅较大,导致低水流对浮板水弹性响应的实际影响增加;从弹性板的迎浪端到中间位置再到尾端,水弹性响应的二阶和三阶标准差在总体水弹性响应标准差中的比重逐渐增加,这说明随着波浪沿着非均匀海底从迎浪侧向尾端传递和变形,结构的非线性水弹性响应越来越突出,进一步证明采用完全非线性数值模型分析不匀均海域上大型浮体水弹性响应的必要性。
(a) 迎浪端
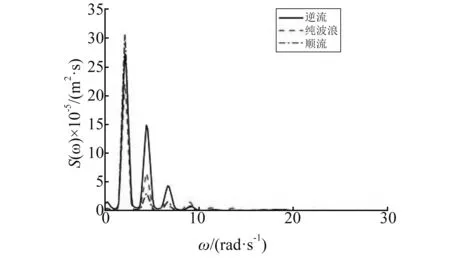
(b) 中间位置
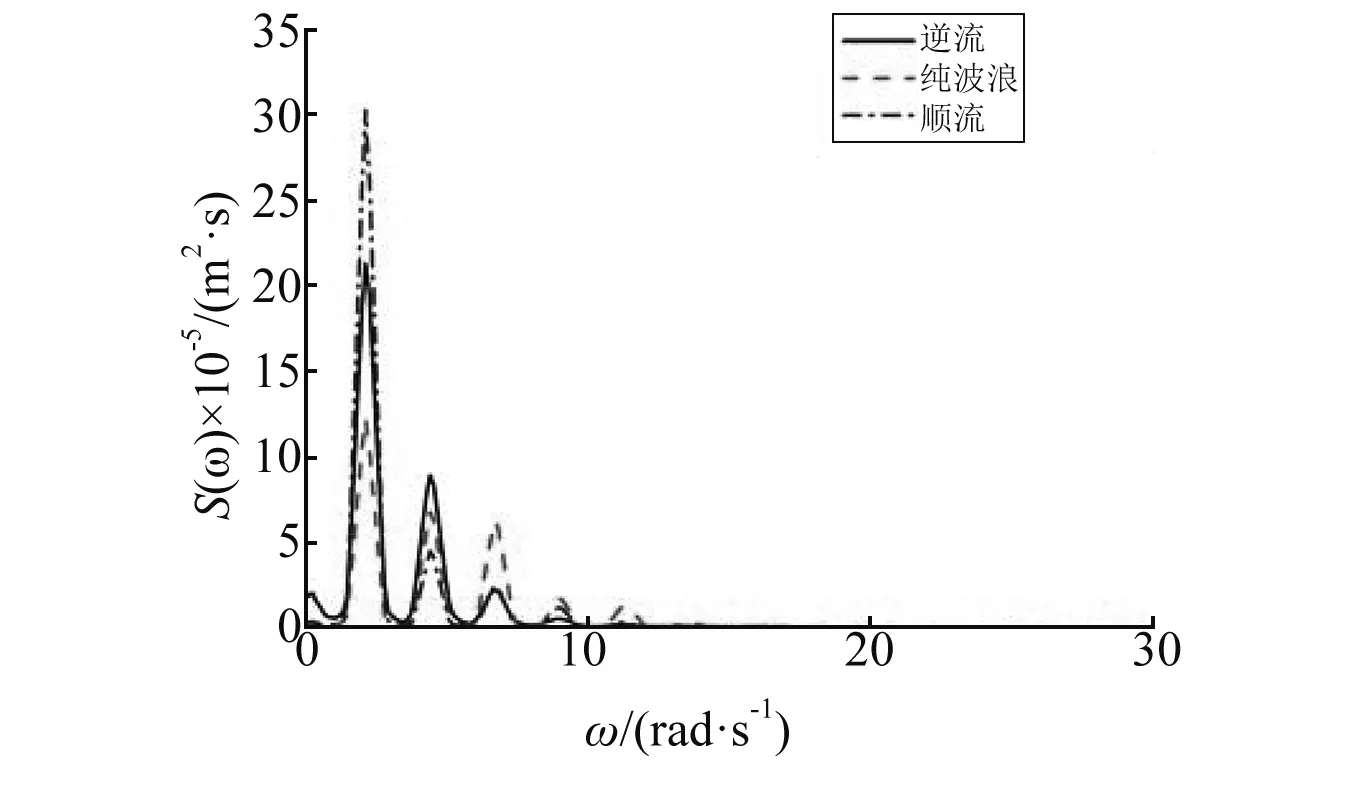
(c) 尾端图11 不同流速时浮板各位置在不均匀海域 中的垂向位移响应谱Fig.11 Hydroelastic response spectra of the plate over variable depth sea-bottom for different currents
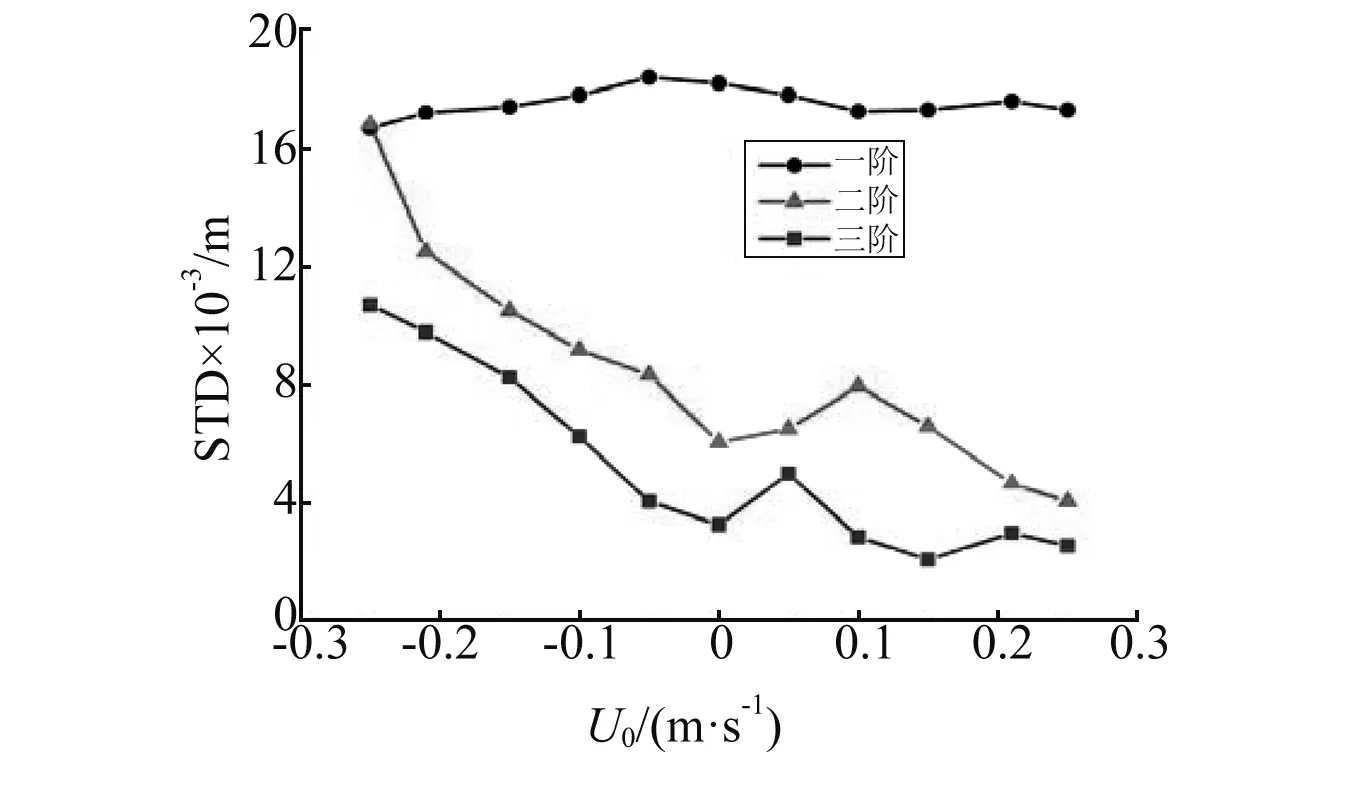
(a) 迎浪端
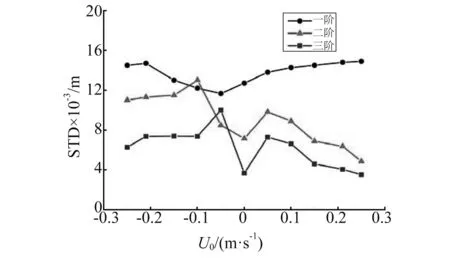
(b) 中间位置
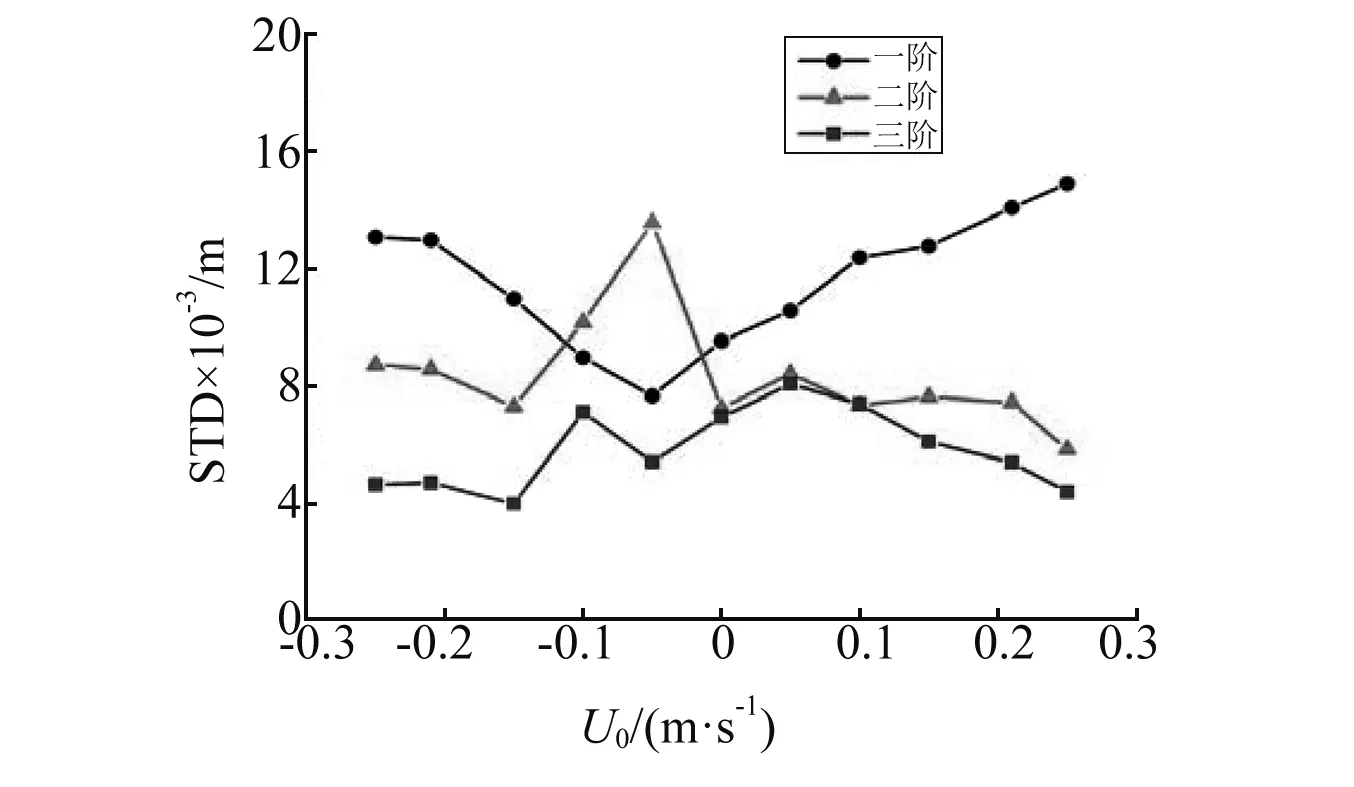
(c) 尾端图12 浮板各位置垂向位移响应谱的一阶、二阶 和三阶标准差随均匀流流速的变化Fig.12 First, second and third harmonic standard deviation (STD) at fore-end, mid-position and back-end of the plate as a function of current velocity
3 结 论
本文基于势流理论和混合欧拉-拉格朗日方法,采用高阶边界元技术建立时域完全非线性的二维数值水槽,并将其应用于研究不均匀海域上的浮板在波流联合作用下的水弹性响应规律。通过与已出版文献的无网格数值算法结果比较,表明本文所建立数值模型的准确性和可行性。进一步研究发现,水流及不匀均海底的存在对浮板水弹性响应会有很大影响:与纯波浪数值结果相比,波浪同向和逆向时浮板的水弹性响应分别具有超前性和滞后性,这是因为顺流时波浪的传播速度加快,而逆向则相反;平底情况下,从逆流到纯波浪再到顺流,浮板波频和倍频响应之间的能量转换逐渐增强;布置不均匀海底时,由于浅水效应导致浮板的水弹性响应较平底情况有明显增加,并且与纯波浪数值结果相比,逆流增强了浮板水弹性响应的非线性特征,而顺流则相反;波流混合传播至不均匀海底时,更多高频和低频的水弹性响应产生,改变了各位置响应频谱的分布,无论是逆流、静水还是顺流中,浮板的基频响应从迎浪端到尾端逐渐减小,高阶响应变化趋势则不尽相同;随着水流流速从逆向到正向逐渐增加,浮板的波频水弹性响应总体呈增加趋势,而二阶和三阶水弹性响应总体趋势下降,这是由于非线性因子波陡随着水流的增加而减小造成的。
总之通过本文的相关研究,发现近海非均匀海域里大型浮体在波流混合作用下的水弹性响应具有极强的非线性特性,证明本文数值方法的可行性和有效性,接下来可进一步分析复杂海洋环境如不规则波浪、聚焦波浪和孤立波浪与水流联合作用的影响。
[1] 崔维成. 超大型海洋浮式结构物水弹性响应预报的研究现状和发展方向[J]. 船舶力学,2002,6(11): 73-90. CUI Weicheng. Current status and future direction in predicting the hydroelastic response of very large floating structures[J]. Journal of Ship Mechanics,2002,6(11):73-90.
[2] WU C, WATANABE E, UTSUNOMIYA T. An eigenfunction expansion-matching method for analyzing the wave-induced responses of an elastic floating plate[J]. Applied Ocean Research, 1995, 17:301-310.
[3] RIYANSYAH M, WANG C M, CHOO Y S. Connection design for two-floating beam system for minimum hydroelastic response[J]. Marine Structures, 2010, 23:67-87.
[4] KARMAKAR D, SOARES C G. Scattering of gravity waves by a moored finite floating elastic plate[J]. Applied Ocean Research, 2012, 34:135-149.
[5] 翟钢军,程勇,马哲. 超大型浮式储油船的水弹性响应预报[J]. 振动与冲击,2014,33(1):141-148. ZHAI Gangjun, CHENG Yong, MA Zhe. Hydroelastic response prediction of very floating oil storage vessel[J]. Journal of Vibration and Shock, 2014, 33(1):141-148.
[6] ZHAO C B, HAO X C, LIANG R F, et al. Influnce of hinged conditions on the hydroelastic response of compound floating structures[J]. Ocean Engineering, 2015, 101:12-24.
[7] WATANABE E, UTSUNOMIYA T, TANIGAKI S. A transient response analysis of a very large floating structure by finite element method[J]. Structural Eng./Earthquake Eng., JSCE 1998, 15(2):155-163.
[8] QIU L C, LIU H. Transient hydroelastic response of VLFS by FEM with impedance boundary conditions in time domain[J]. China Ocean Engineering, 2004, 19(1):1-9.
[9] QIU L C, LIU H. Time domain simulation of transient responses of very large floating structures under unsteady external loads[J]. China Ocean Engineering, 2005, 19(3): 365-374.
[10] KASHIWAGI M. A time-domain mode-expansion method for calculating transient elastic responses of a pontoon-type VLFS[J]. Journal of Marine Science and Technology, 2000, 5: 89-100.
[11] KASHIWAGI M. Transient response of a VLFS during landing and take-off of an airplane[J]. Journal of Marine Science and Technology, 2004, 9:14-23.
[12] ENDO H. The behavior of a VLFS and an airplane during takeoff/landing run in wave condition[J]. Marine Structures, 2000, 13:477-491.
[13] CHENG Y, ZHAI G J, OU J P. Time-domain numerical and experimental analysis of hydroelastic response of a very large floating structure edged with a pair of submerged horizontal plates[J]. Marine Structures, 2014, 39:198-224.
[14] 陈徐均,吴有生,崔维成,等. 海洋浮体二阶非线性水弹性力学分析-系泊浮体主坐标响应的频率特征[J]. 船舶力学, 2002, 6(5):44-57. CHEN Xujun, WU Yousheng, CUI Weicheng, et al. Second order nonlinear hydroelastic analyses of floating bodies-frequency characteristics of the principal coordinates of a moored floating body [J]. Journal of Ship Mechanics, 2002, 6(5):44-57.
[15] 陈徐均,崔维成,JUNCHER JENSEN J,等. 海洋浮体非线性水弹性力学分析-结构非线性的初步考虑[J]. 船舶力学,2003, 7(5):81-90. CHEN Xujun, CUI Weicheng, JUNCHER JENSEN J, et al. Second order nonlinear hydroelastic analyses of floating bodies-the primary consideration of nonlinear structure [J]. Journal of Ship Mechanics, 2003, 7(5):81-90.
[16] LIU X D, SAKAI S. Time domain analysis on the dynamic response of a flexible floating structure to waves[J]. Journal of Engineering Mechanics, 2002, 128(1):48-56.
[17] KYOUNG J H, HONG S Y, KIM B W. FEM for time domain analysis of hydroelastic response of VLFS with fully nonlinear free-surface conditions[J]. International Journal of Offshore and Polar Engineering, 2006, 16(3):168-174.
[18] MOOLLAZADEH M, KHANJANI M J, TAVAKOLI A. Applicability of the method of fundamental solutions to interaction of fully nonlinear water waves with a semi-infinite floating ice plate[J]. Cold Region Science Technology, 2011, 69(1):52-58.
[19] MIRAFZALI F, TAVAKOLI A, MOLLAZADEH M. Hydroelastic analysis of fully nonlinear water waves with floating elastic plate via multiple knot B-splines[J]. Applied Ocean Research, 2015, 51:171-180.
[20] 陈丽芬,宁德志,滕斌,等. 潜堤上波流传播的完全非线性数值模拟[J]. 力学学报, 2011, 43(5):834-843. CHEN Lifen, NING Dezhi, TENG Bin, et al. Fully nonlinear numerical simulation for wave-current propagation over a submerged bar[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011,43(5):834-843.
[21] REDDY J N. An introduction to the finite element method, Third edition[M]. New York: McGraw-Hill, 2005.
[22] NEWMAN J N. Wave effects on deformable bodies[J]. Applied Ocean Research, 1994, 16:47-59.
Nonlinear numerical simulation for wave-current interaction with a floating elastic plate over variable depth sea bottom
CHENG Yong1, JI Chunyan1, ZHAI Gangjun2
(1. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China; 2. Deepwater Engineering Research Center, Dalian University of Technology, Dalian 116024, China)
Hydroelastic analysis of wave-current nonlinear interaction with a floating elastic plate is complex, especially when water waves propagate along uneven sea bottom. The fully nonlinear analysis techniques are widely recognized as a unique approach to predict the accurate hydroelastic responses. A 2D (two-dimensional) time domain fully nonlinear numerical tank using higher-order boundary element method was devoted to solve such a problem in this work. The fourth-order Runge-Kutta time stepping integration scheme with the mixed Eulerian-Lagrangian approach was applied to update the instantaneous free and plate surface. An Euler-Bernoulli-von Karman nonlinear beam model was introduced to determine the fluid pressure imposed on the fluid-structure interface. In order to obtain derivatives of plate surface, the plate displacement was interpolated using a series of modal functions, and the modal amplitudes were solved by applying the Galerkin scheme. The numerical solutions were validated against existing meshless numerical results. Further calculations were then conducted to examine the effects of currents and the uneven topography on the displacement nonlinearity of the plate. Finally, the higher harmonic displacements were investigated with the various current velocities.
floating elastic plate; higher-order boundary element method; time domain fully nonlinear; hydroelastic responses; wave-current interaction; uneven sea-bottom
国家自然科学基金重大项目(51490672);国家自然科学基金(51579122);江苏省船舶先进设计制造技术重点实验室基金(CJ1506)
2016-02-23 修改稿收到日期: 2016-04-22
程勇 男,博士,讲师,1986年生
TU311
A
10.13465/j.cnki.jvs.2017.12.019
