隧洞开挖爆破空气超压诱发围岩振动机理

陈 明， 何文学， 卢文波， 王高辉， 郭天阳， 冷振东

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2.武汉大学 水工岩石力学教育部重点实验室，武汉 430072)

隧洞开挖爆破空气超压诱发围岩振动机理

陈 明1,2， 何文学1,2， 卢文波1,2， 王高辉1,2， 郭天阳1,2， 冷振东1,2

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2.武汉大学 水工岩石力学教育部重点实验室，武汉 430072)

基于河北丰宁抽水蓄能电站地质探洞中爆破试验获取的监测数据，理论分析和数值模拟研究了隧洞开挖爆破空气冲击波超压诱发围岩振动的机理及特性。结果表明，小断面隧洞爆破空气冲击波超压较大并将诱发围岩振动，该振动具有振速高、持续时间长和衰减慢等特征；空气冲击波超压诱发的围岩受迫振动发生时间受空气冲击波传播速度控制；诱发振动可分为空气冲击波超压作用于前部围岩产生并经围岩传播过来的振动，和空气冲击波超压传播到围岩壁面直接引起的振动。数值模拟发现受迫振动经围岩传播时衰减很快，所以测点的振动主要是由于空气冲击波超压直接作用于洞壁造成的围岩振动。

钻孔爆破；隧洞；振动速度；空气冲击波超压

水利水电、交通、采矿等工程领域均涉及到大量的隧洞开挖工作，隧洞开挖爆破中会产生地震波、空气冲击波超压、爆破飞石、有害气体等有害效应。实际爆破中产生的能量只有20%～30%用来破碎岩石，其余能量被地震波、空气冲击波超压、爆破飞石等消耗掉，其中地震波和空气冲击波超压携带能量最多，不仅影响地下洞室的安全和稳定，而且危及人类生命和财产的安全。

众多研究者对钻孔爆破振动及空气冲击波超压传播规律进行了研究。闫鸿浩等[1-3]采用现场试验分析了爆破振动的传播规律； Resende等[4]提出了应力波传播途径和局部峰值在爆破振动控制中的重要性；Ahmed等[5]提出了爆破振动作用下隧洞中喷射混凝土的安全控制措施，赵振国等[6]研究了爆破振动对二次喷护结构的影响。隧洞开挖爆破空气冲击波超压方面的研究也有大量成果，Pennetier等[7]论证了隧道中爆炸远区空气冲击波传播规律类似为一维应力波。Kuzu等[8-9]研究了隧洞爆破开挖空气冲击波超压对人和结构的危害。张文煊等[10]研究了巷道爆破中空气冲击波超压的传播规律，认为空气冲击波超压在沿巷道传播时，在开挖面近区衰减最快，当距离较远时，冲击波的衰减比在自由空间慢。田志敏等[11]通过数值模拟研究了隧道内爆炸空气冲击波超压流场，分析了上下壁面压力峰值随爆心距的衰减规律。杨科之等[12]用量纲分析法研究了坑道内爆炸空气冲击波超压的传播规律，得到坑道内冲击波的超压峰值和作用时间较自由空气中都有增大。朱传云[13]在研究隧洞轮廓爆破过程中，监测到空气冲击波超压会造成围岩壁面振动，并将此解释为空气冲击波超压诱发的拍振现象。Albert等[14]的研究也发现，在近地表爆炸时地面先后产生两次振动，第一次振动是由于地震波引起，第二次振动由空气中传播的压力即空气超压所引起。

综合以上分析可见，已有研究重点在爆破地震波和空气冲击波超压的传播与衰减规律，对于隧洞爆破开挖空气冲击波超压诱发的围岩振动的研究相对较少。本文基于河北丰宁抽水蓄能电站地下厂房地质探洞钻孔爆破试验资料，采用理论分析与数值模拟相结合的方法，研究隧洞开挖爆破中空气冲击波超压诱发围岩振动的机理及特性，为合理评价空气冲击波超压导致的振动对围岩稳定及其他设施安全的影响提供参考。

1 丰宁抽水蓄能电站二期工程钻孔爆破试验

丰宁抽水蓄能电站位于中国河北省丰宁满族自治县境内，丰宁抽水蓄能电站规划装机容量3 600 MW，为世界上装机容量最大的抽水蓄能电站。为了研究地

下厂房系统施工过程中的爆破有害效应影响，利用工程地质探洞，进行了钻孔爆破试验，分析振动及空气冲击波超压的传播与衰减规律。

1.1 爆破试验设计

地下厂房地质探洞的掌子面进行浅孔掏槽爆破试验，马蹄形探洞断面高和宽分别为2.1 m与1.8 m。掏槽爆破采用中间有大空孔的直孔掏槽方式，炮孔布置在探洞开挖掌子面，如图1和图2所示。使用乳化炸药，每个炮孔装两发非电半秒延期雷管，采用0.5 s微差起爆网路，分两段起爆，起爆网路图，如图2所示，爆破设计参数，见表1。

图1 炮孔位置及监测点布置图Fig.1 Arrangement of blastholes and measurement points

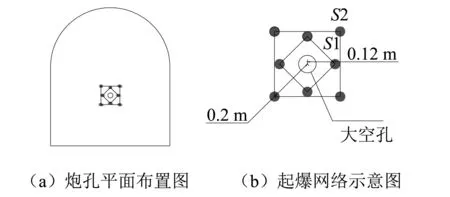
图2 浅孔掏槽爆破炮孔平面布置及起爆网络示意图Fig.2 Arrangement of shallow cut blastholes and sketch map of detonating network表1 水平钻孔爆破试验参数表Tab.1 Horizontal drilling blasting experiment parameters

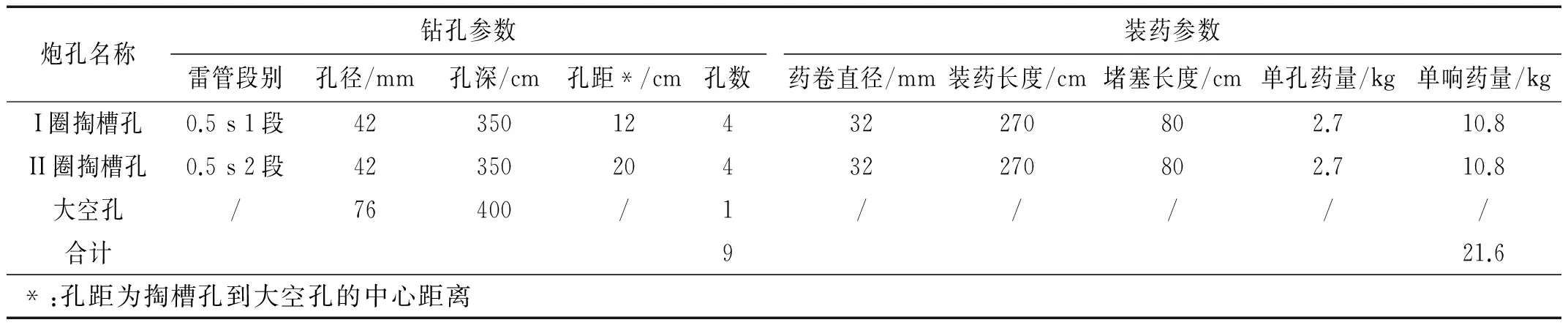
炮孔名称钻孔参数雷管段别孔径/mm孔深/cm孔距*/cm孔数装药参数药卷直径/mm装药长度/cm堵塞长度/cm单孔药量/kg单响药量/kgI圈掏槽孔0.5s1段4235012432270802.710.8II圈掏槽孔0.5s2段4235020432270802.710.8大空孔/76400/1/////合计921.6*:孔距为掏槽孔到大空孔的中心距离

1.2 爆破振动及空气冲击波超压测试

在探洞中布置一条爆破振动测试线，如图1所示。每个测点相对于爆源具有水平径向、水平切向及垂直向三个方向，获得了掏槽爆破的爆破振动的传播与衰减规律。试验中在图1所示的3#～9#测点布置TC-4850爆破测振仪，其中5#及8#测点由于施工影响，没有测得数据。另外，在图1所示的1#、2#和10#测点位置，利用Minimate Pro4振动及过压监测仪，监测爆破振动速度。

图1所示的1#、2#和10#测点同时用作空气冲击波超压的监测点，测试空气冲击波超压的分布规律。

1.3 爆破试验数据分析

现场测试得到了爆破振动及空气冲击波超压测试数据。需要说明的是，实际试验时由于现场条件限制，炮孔堵塞段仅使用了泡湿的纸片，测得空气冲击波超压峰值严重超过设备的量程，但测试结果显示了该隧洞中空气冲击波超压峰值大、持续时间长的特点。

选取典型测点2#和3#振动波形图，如图3所示。并分析所有测点的振动波形可知，振动波形都可以分为三段。

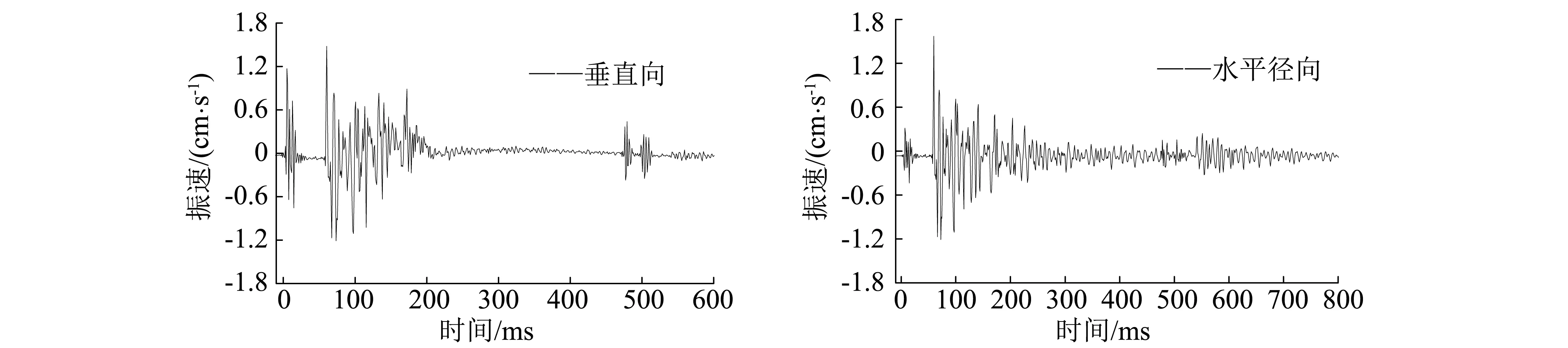
(a) 2#测点质点振动速度时程曲线

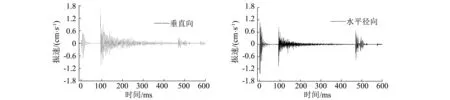
(b) 3#测点质点振动速度时程曲线图3 典型测点质点振动速度时程曲线(2#、3#测点)Fig.3 Recoded particle vibration velocity-time histories of typical measurement points (at 2# and 3#)表2 各测点空气冲击波超压传播速度Tab.2 The propagating velocity of air overpressure at all measurement points

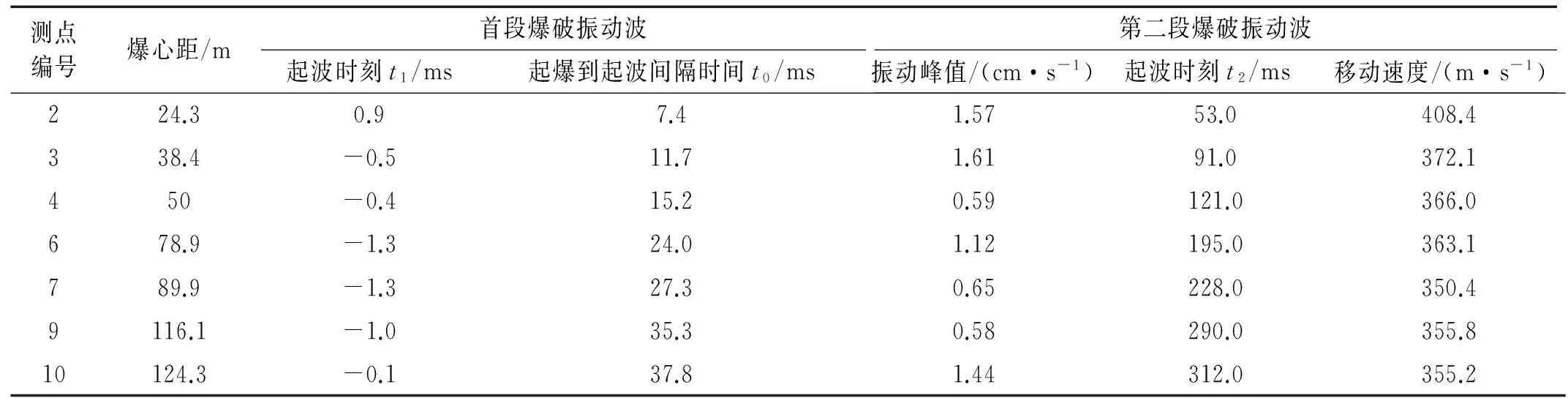
测点编号爆心距/m首段爆破振动波起波时刻t1/ms起爆到起波间隔时间t0/ms第二段爆破振动波振动峰值/(cm·s-1)起波时刻t2/ms移动速度/(m·s-1)224.30.97.41.5753.0408.4338.4-0.511.71.6191.0372.1450-0.415.20.59121.0366.0678.9-1.324.01.12195.0363.1789.9-1.327.30.65228.0350.49116.1-1.035.30.58290.0355.810124.3-0.137.81.44312.0355.2

由试验设计可知，起爆网路仅设计了两段，而实际监测到了三段振动波形，考虑到起爆网路中采用的是半秒延期雷管，半秒延期雷管的误差较大，分析认为振动波形中的第一段和第三段是爆破地震波产生的振动。

分析第二段振动波的特征发现，其具有振速较高、持续时间长和衰减较慢的特点。第二段振动波的特性与爆破地震波的振动特性相比，存在比较明显的差异，根据朱传云及Albert的研究成果，初步判断认为，该段振动波的产生与空气冲击波超压有密切的联系。

2 丰宁试验空气超压峰值及其诱发振动的理论分析

2.1 空气冲击波超压诱发振动的移动速度

统计所有测点第一段和第二段振动的起波时刻见表2，可以发现，第二段振动在洞室轴线方向出现的时刻有一定规律。根据空气冲击波超压的传播特性，初步判断第二段波形是由于首段爆破产生的空气冲击波超压在小断面洞室中传播诱发的振动。爆破试验的第二段爆破后也有空气冲击波，但第一段爆破产生的空腔及临空面作用，大大降低了空气冲击波的强度。

根据地震波理论，围岩中的地震波纵波波速vP，可由式(1)估算

(1)

式中：E为岩石弹性模量；ν为泊松比；ρ为岩石密度。试验区岩体E =24GPa；泊松比为0.24；密度为2 610kg/m3。

由此先计算得首段波在岩体中传播的纵波波速约为3 292m/s，结合已知爆心距和各时间求出第二段振动在隧洞轴线方向的移动速度，结果如表2所示(其中1#测点由于距爆源较近，第一段与第二段重叠，分不清第二段起波时间)。可以发现第二段振动波的移动速度略大于音速。众所周知，爆破产生的高温高压气体随着岩块冲出，爆破瞬间在爆源近区压缩周围空气，使周围空气形成压力很高的初始空气冲击波超压，接着从爆心传播出去，传播速度略大于扰动空气的声速[15]，并且随爆心距增加而衰减，根据空气冲击波超压的传播特性，初步判断第二段波形是由于首段爆破产生的空气冲击波超压在小断面洞室中传播诱发的振动。

2.2 隧洞中空气冲击波超压的估算

实际监测中未获得空气冲击波超压峰值，为验证上述分析结论，需要采用其他方法分析爆破试验时各测点处的空气超压峰值。在井下和巷道爆破中，《爆破安全规程实施手册》[16]中的空气冲击波超压计算公式为

(2)

式中：ΔP为井下空气冲击波超压，kPa；q为TNT炸药重量，kg；试验所用为乳化炸药，乳化炸药与TNT之间的当量系数取0.708，转化为TNT炸药q=7.65kg；my为炸药能量转换为冲击波系数；R为距爆源距离，m；∑S为与药包毗连的巷道总面积，m2；β 为巷道表面粗糙性系数；dn为巷道的直径，m。

计算参数，如表3所示。利用上述空气冲击波超压计算公式计算得丰宁试验中2#测点超压峰值为93.2kPa。

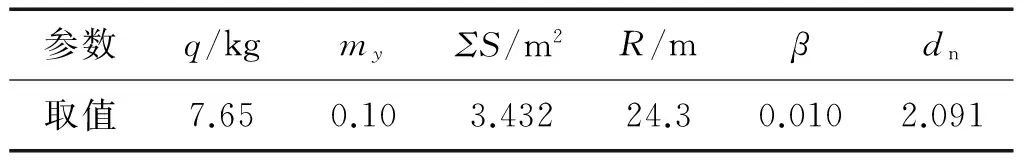
表3 井下空气冲击波超压计算参数取值Tab.3 Underground air shock wave calculation parameter

结合上述公式，计算空气冲击波超压沿隧洞方向传播140 m的峰值衰减曲线，如图4所示。由图4可知，空气冲击波超压峰值沿隧洞方向衰减较快。而且由式(2)也可知，隧洞断面面积增大，空气冲击波超压将迅速降低。

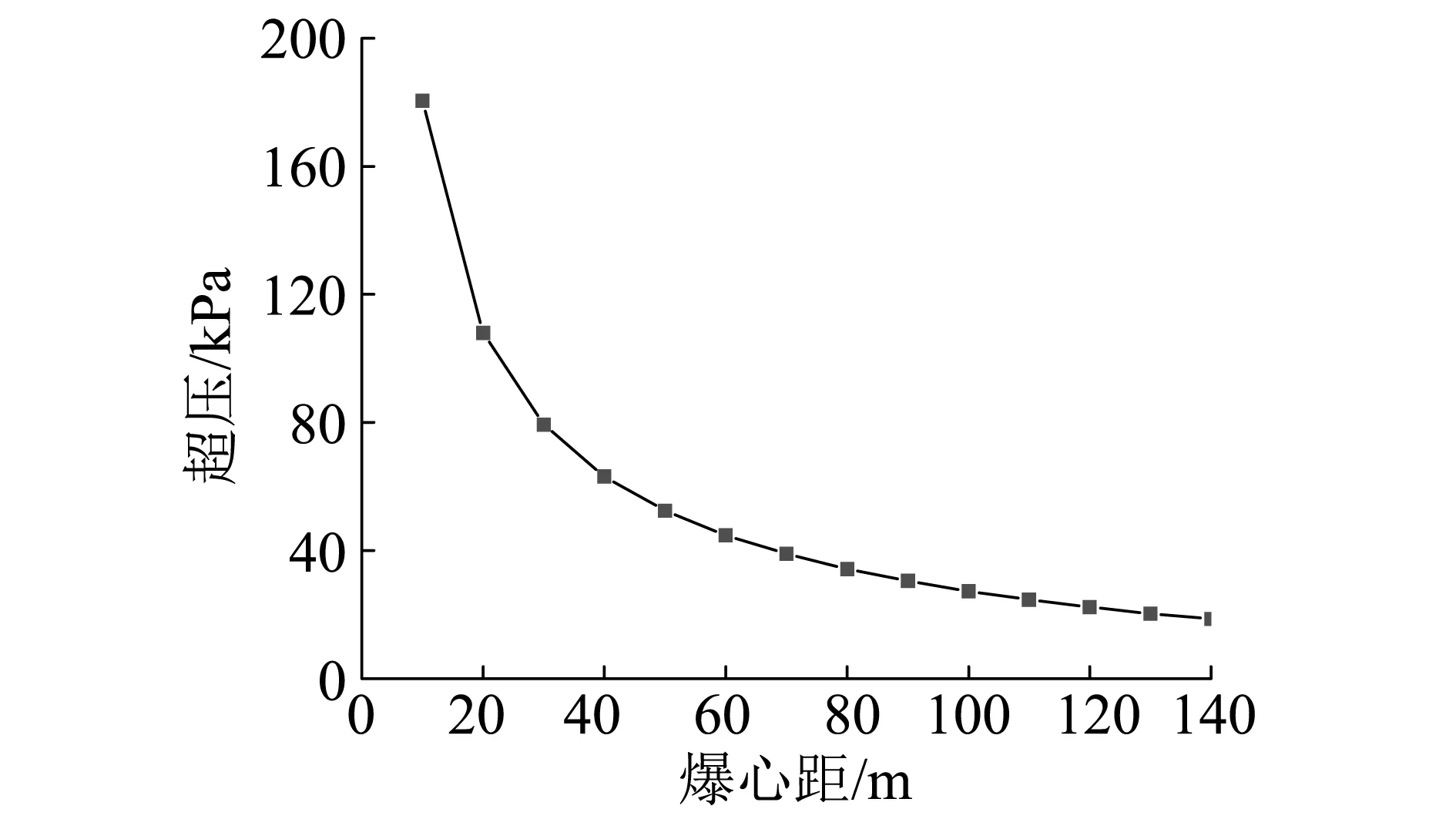
图4 空气冲击波超压沿隧洞方向传播的峰值衰减曲线Fig.4 Attenuation curve of peak air shock wave propagating along the tunnel

对于隧洞围岩壁面的某一点，空气冲击波超压为扰动荷载，在该点可产生两次振动，首先出现的振动是空气冲击波超压作用于前部围岩产生的经隧洞围岩传播过来的振动波，其后出现的是空气冲击波超压传播到该点由空气超压直接引起的振动。应用一维应力波理论估算空气超压直接诱发的振动峰值。基于一维应力波理论，围岩应力与振动速度具有如下规律：

σ=ρCv

(3)

式中：σ为围岩应力；ρ为介质密度；C为纵波波速；v为质点振动速度。

弹性应力波从一种介质传到另一种介质时，在界面上会发生反射和透射。由于空气冲击波波阻抗远小于岩体波阻抗。所以透射应力扰动近似为入射应力扰动的2倍。

以2#测点处的相关参数为基础进行分析，取式(2)计算得到空气超压峰值为93.2kPa，考虑空气冲击波在壁面发生的反射和透射，实际透射的应力扰动最大值约为186.4kPa。该处围岩密度变化范围2 250～2 650kg/m3，纵波波速2 500～5 000m/s。代入式(3)计算，隧洞围岩壁面的质点振动速度峰值约为1.41～3.39cm/s。此范围与实际监测到的振动数据基本一致，进一步说明实测的第二段振动波形，是由空气冲击波超压作用于隧洞围岩上所诱发的围岩受迫振动。

同理，利用式(2)计算其他测点振动峰值范围，并与实测值作比较，如图5所示。可以得到，实测振速峰值基本处于经验公式计算所得振速峰值范围内，由于小断面隧洞中空气冲击波超压衰减相对较慢，才导致距离爆源较远处空气冲击波超压诱发的围岩质点峰值振动速度略大于计算得到的振速峰值。

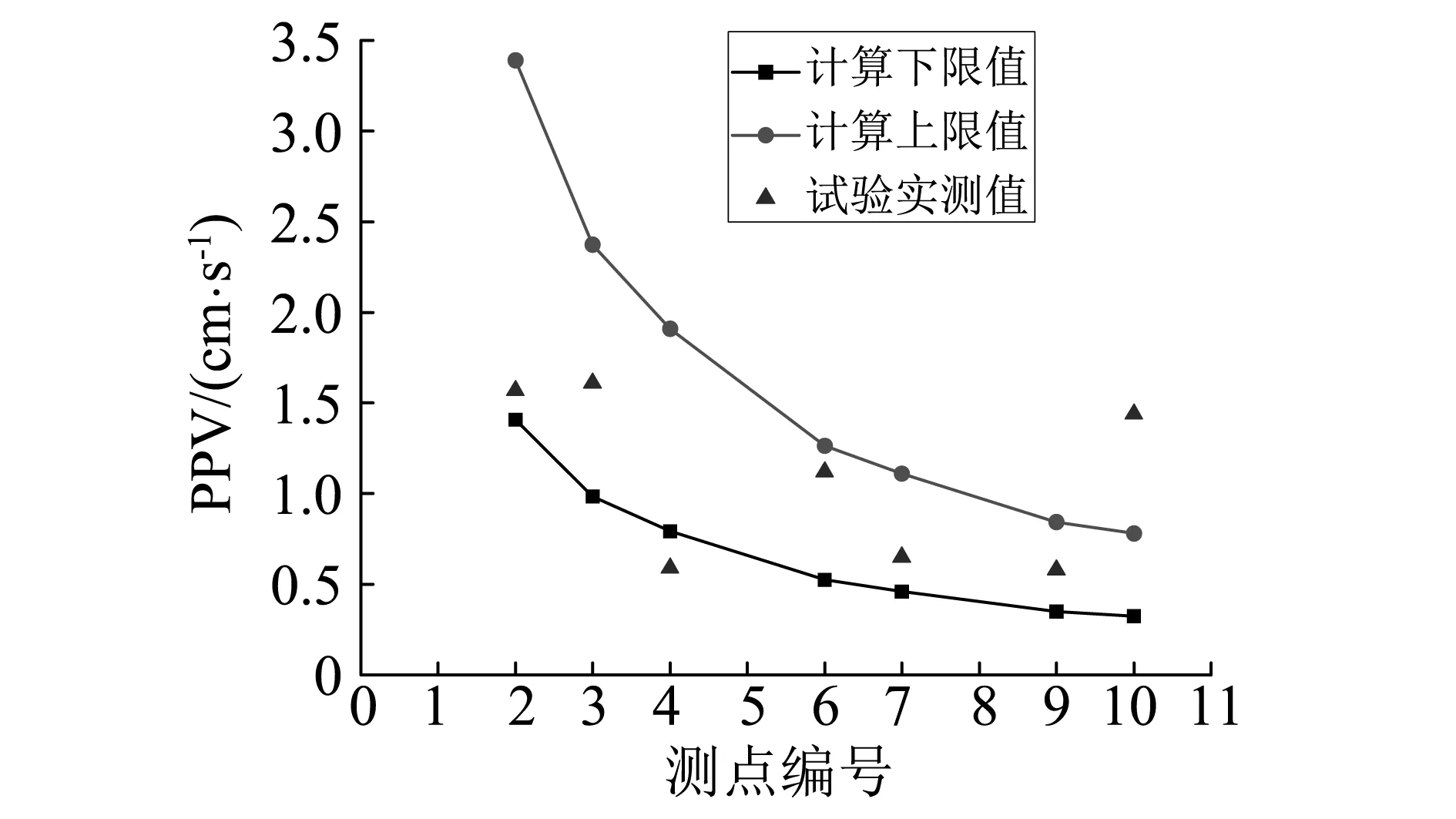
图5 计算与实测振动峰值的对比Fig.5 Comparison of PPV between theoretical predicting and site monitoring at different measurement points

3 空气冲击波超压诱发围岩振动的数值模拟

3.1 数值分析模型与参数

采用数值模拟方法进一步分析空气冲击波超压诱发围岩振动的机理及其特性，比较超压作用于测点直接诱发的振动和其经过围岩传播到更远测点时衰减后的振动。应用Ansys-Lsdyna软件，根据地质探洞尺寸及围岩属性，取距离开挖掌子面24.3～39.3m范围内的围岩，建立数值分析模型，模型大小为20m×20m×15m，围岩四周和前后面均加无反射边界，如图6。探洞断面为1.8m×2.1m的马蹄形。在模型2# 测点直接加载，而在3#测点不加荷载，观察2# 测点的诱发振动和其经过围岩传播到3# 测点时衰减后的振动。模拟中选取实测2# 测点垂直向0～300ms振动速度时程曲线作为速度荷载。作用在距离开挖掌子面24.3m的模拟2# 测点所在断面节点上，速度荷载曲线，如图7所示。

图6 计算模型Fig.6 Numerical simulation model

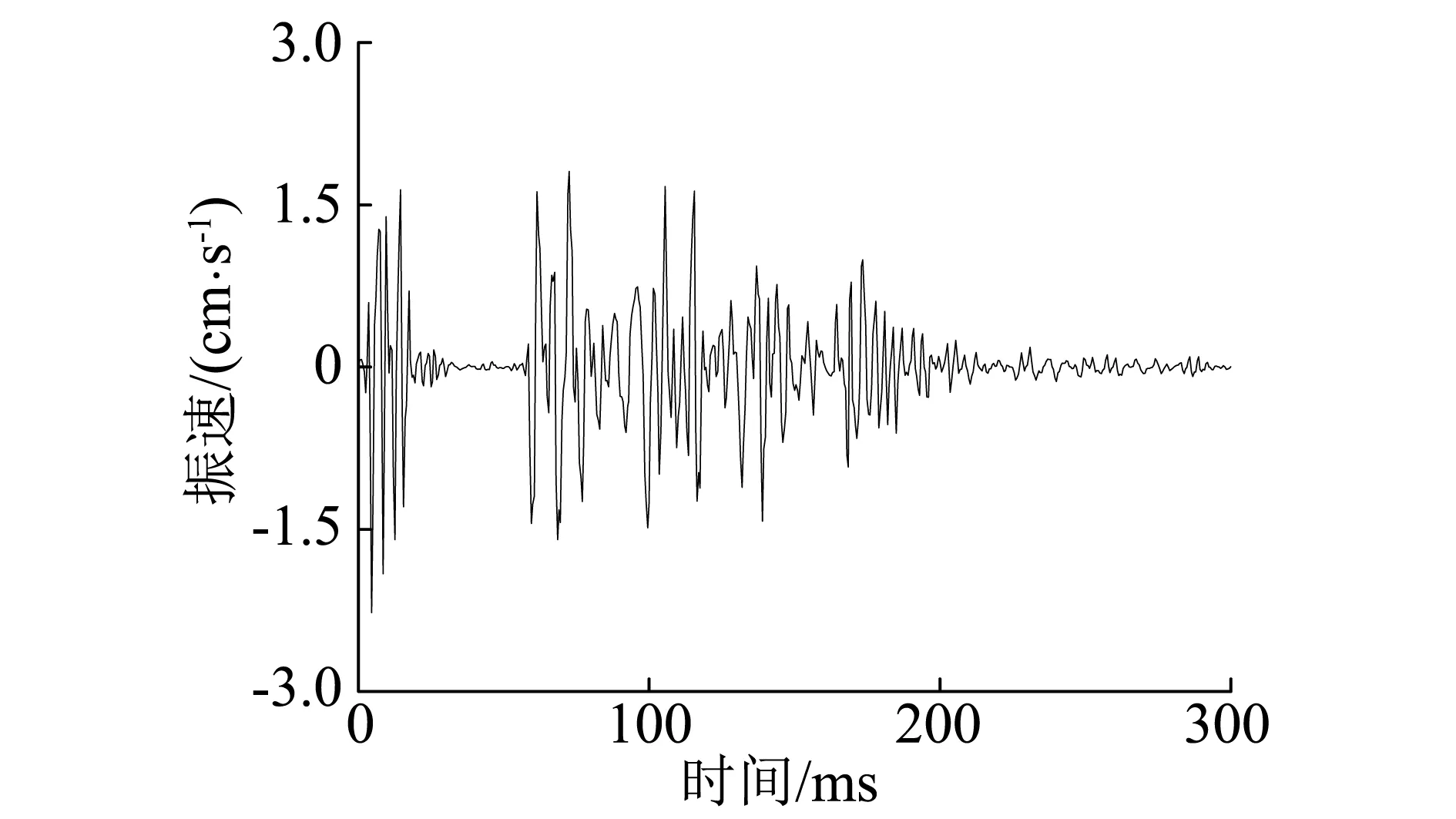
图7 模拟速度荷载曲线(2#测点垂直向前300 ms)Fig.7 Velocity-time histories of modeling (vertical, at 2#, 0-300 ms)

根据中国电建集团北京勘测设计研究院提供的试验区围岩物理力学指标建议值，数值模拟采用的岩体物理力学参数，如表4所示。

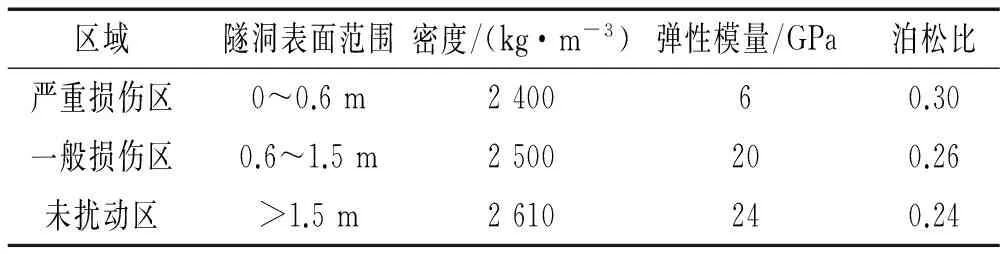
表4 岩体物理力学参数Tab. 4 Physical and mechanical parameters of rock mass

3.2 数值模拟结果分析

依次沿洞轴线方向距离开挖面24.3 m、38.4 m(3#测点)处取洞底表面中间节点的振动速度时程曲线，如图8所示。

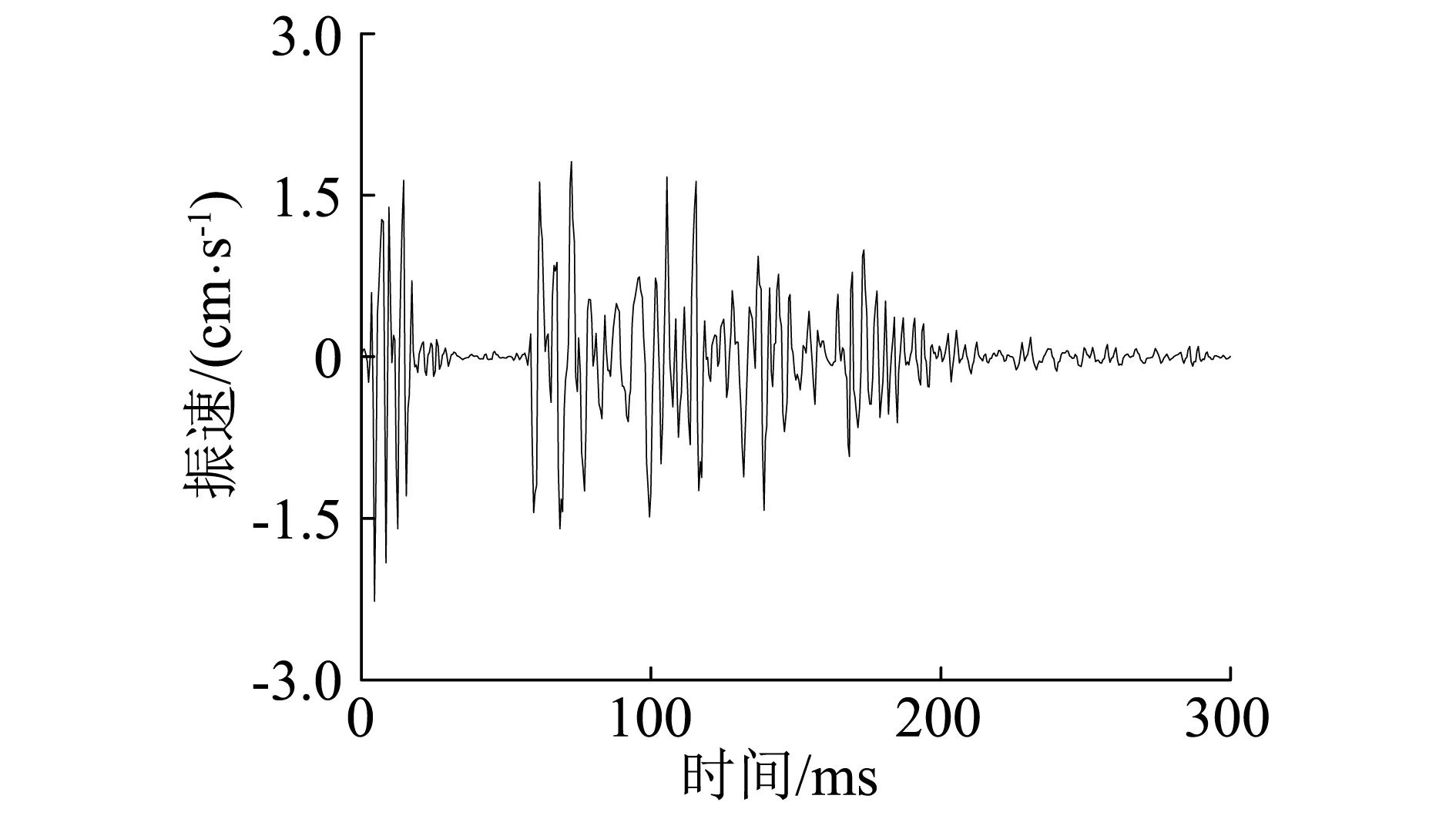
(a)2#测点处节点振动速度时程图

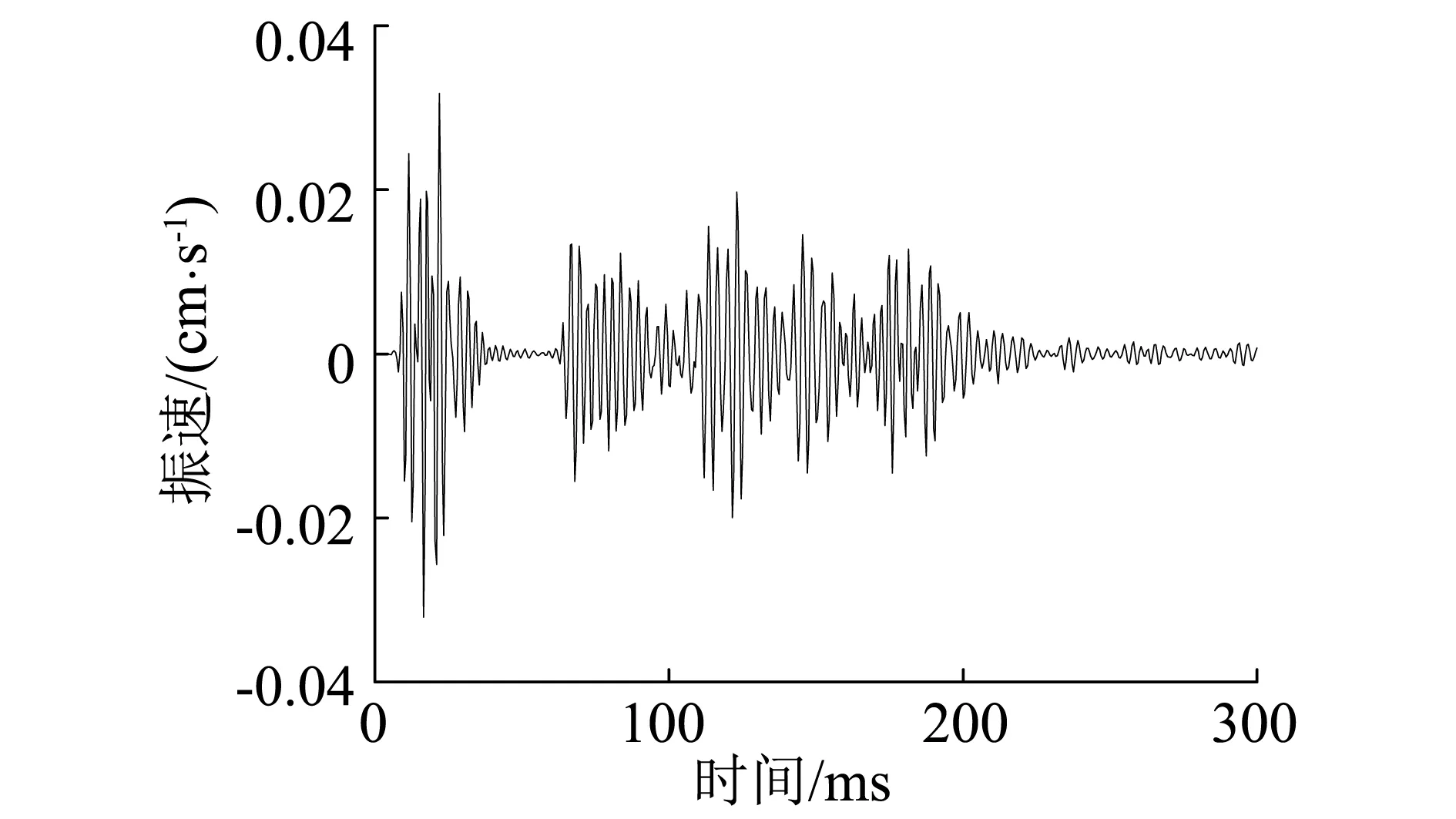
(b) 3#测点处节点振动速度时程图 图8 典型点处节点振动速度时程图Fig.8 Simulated particle vibration velocity-time histories of the typical points

对比图8(a)～图8(b)，可见荷载施加处即2#测点处垂直向壁面质点振动峰值为1.650 cm/s，与该点现场试验实测的振动峰值基本一致，并且与一维应力波理论分析的结果相当。此振动沿岩石传播到3#测点处时质点振动峰值只有0.020 cm/s，对比地震波造成的振动，可以得到空气冲击波超压直接作用点造成的振动峰值与地震波造成的振动峰值接近甚至更大，而且空气冲击波超压诱发的围岩振动沿洞壁方向传播过程中衰减很快。但是，实际空气冲击波超压在隧洞空气中传播时，由于洞壁反射作用，空气冲击波超压的衰减较慢，导致空气冲击波超压诱发的围岩振动持续时间很长。可见，现场试验中监测得到的第二段振动波形主要是由于空气冲击波超压直接作用于洞壁造成的壁面振动。

4 结 论

根据以上分析，可得以下结论：

(1) 小断面隧洞中，爆破开挖容易产生较大的空气冲击波超压，空气冲击波超压作用于隧洞围岩壁面，将诱发围岩振动，这种振动峰值出现的时间受空气冲击波超压的传播速度控制。实际监测中，监测点获取的空气冲击波超压诱发的振动波形的出现时间，随着爆心距的增大而不断推迟。

(2) 空气冲击波超压诱发的围岩振动，具有振动振速较高、持续时间长和衰减较慢的特点。

(3) 空气冲击波超压诱发的围岩振动，可分为空气冲击波超压作用于前部围岩产生的经隧洞围岩传播过来的振动，和空气冲击波超压传播到围岩壁面直接引起的振动。经围岩传播的振动衰减很快，实测的振动主要是由于空气冲击波超压直接作用于洞壁造成的围岩振动。

[1] 闫鸿浩, 李晓杰, 曲艳东, 等. 爆破振动速度测试精细分析[J]. 岩土力学, 2007, 28(10): 2091-2094.YANHonghao,LIXiaojie,QUYandong,etal.Fineanalysisofblastingvibrationvelocitytesting[J].RockandSoilMechanics, 2007, 28(10): 2091-2094.

[2] 李新平, 张成良, 陈先仿, 等. 复杂地下洞室群爆破地震波传播的现场试验研究[J]. 岩石力学与工程学报, 2005, 24(增刊1): 4700-4704. LI Xinping, ZHANG Chengliang, CHEN Xianfang, et al. In-situ experimental study on transmission of blasting vibration wave in groups of tunnels under complicated conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Sup1): 4700-4704.

[3] 宋全杰, 李海波, 李俊如, 等. 层理对爆破振动传播规律的影响[J]. 岩石力学与工程学报, 2012, 31(10): 2103- 2108. SONG Quanjie, LI Haibo, LI Junru, et al. Influence of stratification on attenuation law of blasting vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(10): 2103-2108.

[4] RESENDE R, LAMAS L, LEMOS J, et al.Stress wave propagation test and numerical modelling of an underground complex[J]. International Journal of Rock Mechanics and Mining Sciences, 2014: 26-36.

[5] AHMED L, ANSELL A, Vibration vulnerability of shotcrete on tunnel walls during construction blasting[J]. Tunnelling and Underground Space Technology, 2014, 42: 105-111.

[6] 赵振国,杨建华,卢文波, 等. 基于爆破振动影响评价的深埋隧洞围岩二次喷护时期选择[J]. 振动与冲击, 2015, 34(7): 8-14. ZHAO Zhenguo, YANG Jianhua, LU Wenbo, et al. Selection of spraying time for permanent shotcrete in deep-buried tunnels based on evaluation of the influence of blasting vibration[J]. Journal of Vibration and Shock, 2015, 34(7): 8-14.

[7] PENNETIER O, WILLIAM-LOUIS M, LANGLET A. Numerical and reduced-scale experimental investigation of blast wave shape in underground transportation infrastructure[J]. Process Safety and Environmental Protection, 2015,94: 96-104.

[8] KUZU C, GUCLU E. The problem of human response to blast induced vibrations in tunnel construction and mitigation of vibration effects using cautious blasting in half-face blasting rounds[J]. Tunnelling and Underground Space Technology, 2009, 24(1): 53-61.

[9] FARAMARZI F, FARSANGI M A E, MANSOURI H. Simultaneous investigation of blast induced ground vibration and airblast effects on safety level of structures and human in surface blasting[J]. International Journal of Mining Science and Technology, 2014, 24(5): 663-669.

[10] 张文煊, 刘美山, 张正宇, 等. 水电工程开挖爆破空气冲击波的作用原理与防护[J]. 工程爆破, 2008(4): 82-85. ZHANG Wenxuan, LIU Meishan, ZHANG Zhengyu, et al. Underlying principle and protection of blasting air shock-wave in water-power engineering[J]. Engineering Blasting, 2008(4): 82-85.

[11] 田志敏, 邬玉斌, 罗奇峰. 隧道内爆炸冲击波传播特性及爆炸荷载分布规律研究[J]. 振动与冲击, 2011, 30(1): 21-26. TIAN Zhimin, WU Yubin, LUO Qifeng. Characteristics of in-tunnel explosion-induced air shock wave and distribution law of reflected shock wave load[J]. Journal of Vibration and Shock, 2011, 30(1): 21-26.

[12] 杨科之, 杨秀敏. 坑道内化爆冲击波的传播规律[J]. 爆炸与冲击, 2003(1): 37-40. YANG Kezhi, YANG Xiumin. Propagation characteristics of blast wave in gallery[J]. Journal of Vibration and Shock, 2003(1): 37-40.

[13] 朱传云. 预裂与光面爆破对围岩的影响[J]. 爆破, 1994(2):33-39. ZHU Chuanyun. Effect and analysis of surrounding rock from pre-split and smooth blasting[J]. Blasting, 1994(2): 33-39.

[14] ALBERT D G, TAHERZADEH S, ATTENBOROUGH K, et al. Ground vibrations produced by surface and near-surface explosions[J]. Applied Acoustics, 2013, 74(11): 1279-1296.

[15] 傅建秋, 胡小龙, 刘翼. 防护条件下爆破冲击波衰减规律研究[J]. 爆破, 2007(2): 14-17. FU Jianqiu, HU Xiaolong, LIU Yi. Study of the decay law of blasting shock wave under protection[J]. Blasting, 2007(2): 14-17.

[16] 汪旭光, 于亚伦, 刘殿中. 爆破安全规程实施手册[M]. 北京： 人民交通出版社， 2004.

Studies on the vibration of tunnel surrounding rock induced by air overpressure

CHEN Ming1,2, HE Wenxue1,2, LU Wenbo1,2, WANG Gaohui1,2, GUO Tianyang1,2, LENG Zhendong1,2

(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China；2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering Ministry of Education, Wuhan University, Wuhan 430072, China)

On the basis of monitoring in the blasting test of Feng-ning Pumped Storage Power Station, the air overpressure induced vibration of surrounding rock during tunnel blasting excavation was studied through theoretical analysis and numerical simulation. Air overpressure generated during blasting excavation in a narrow-bore tunnel was large enough to cause the vibration of surrounding rock, which was characterized by high peak particle vibration velocity (PPV), long duration, and slow attenuation. The arrival time of air overpressure induced vibration was determined by the propagating velocity of air shock wave. There were two kinds of air overpressure induced vibration at a certain point, the first was the arrival of the air overpressure induced vibration acting on the surrounding rock of front tunnel, the later was caused by the air overpressure direct acting on the measurement point. The numerical study reveals that vibration attenuates very quickly when propagating in rock, so the vibration waveform recorded in site experiment is mainly air overpressure induced vibration by directly acting on the tunnel surrounding rock.

drill and blast; tunnel; vibration velocity; air overpressure

国家自然科学基金面上项目(51279146；51479147)；新世纪优秀人才支持计划资助(NCET-2012-0425)

2015-11-13 修改稿收到日期： 2016-04-25

陈明 男，博士，教授，1977年生

E-mail: whuchm@whu.edu.cn

TD 235.1

A

10.13465/j.cnki.jvs.2017.12.003