滤波算法的比较及仿真
2017-06-19岳海燕周遵四
岳海燕,姚 红,周遵四
(中国兵器装备集团(成都)火控技术中心 ,四川 成都 611731)
滤波算法的比较及仿真
岳海燕,姚 红,周遵四
(中国兵器装备集团(成都)火控技术中心 ,四川 成都 611731)
文章对雷达系统中常用的卡尔曼滤波、最小二乘滤波算法进行了简单介绍和比较。分别应用算法进行预测,并使用MATLAB对预测得到的数据进行仿真。
卡尔曼滤波;最小二乘滤波;预测
1 雷达数据处理概述
雷达数据处理包括雷达测量数据的滤波、平滑、预测等,这些处理可以有效地抑制测量过程中引入的随机误差,精确估计目标位置和有关的运动参数,预测目标下一时刻的位置,实现对目标的高精度实时跟踪。最早的雷达数据处理方法是在19世纪初叶,高斯提出的最小二乘法。1975年,高斯首次运用最小二乘法预测神谷星轨道,开创了用数学方法处理观测和实验数据的科学领域。20世纪60年代以后,随着数字技术和估计理论的发展,卡尔曼等人将状态变量分析方法引入滤波理论中,得到了最小均方误差估计问题的时域解。卡尔曼滤波理论可用于非平稳和多变量的场合,而且卡尔曼滤波具有递推结构,因此特别适合于计算机解算。由于这些原因,卡尔曼滤波已经成为数据处理的主要技术。本文重点介绍卡尔曼滤波和最小二乘滤波对线性系统下的基本滤波方法,同时完成数据的仿真、预测。
2 卡尔曼滤波及仿真
本文所采用的数据,其先验统计特性一无所知,数据机动性较强,无规律。卡尔曼滤波是一种递推式的滤波器,由维纳滤波演变而来。它不仅适用于实时的预测与滤波,而且特别适合于在数字计算机上实现,计算量小,实时性强。同时可用于线性时变系统,其统计模型是状态方程和观测方程。
(1)状态方程。

式中:W(K)表示白噪声矢量,T表示数据间隔周期。(2)观测方程。

(c)滤波方程组。

式中:Q(K)表示系统噪声协方差矩阵;R(K)表示观测协方差矩阵;起始条件:X0(0)=X0。
3 最小二乘滤波及仿真
本文分别采用三阶多项式和二阶多项式对上述数据进行滤波,并将其结果进行比较。综合比较结果,发现二阶多项式滤波效果较好。最小二乘滤波算法如下:

其中D是俯仰角,q是方位角。
先求俯仰角,先给出n对已知测量值(Di,ti),要求确定参数D0,a,b的值,用最小二乘法,使

解此线性方程,即可求的D0,a,b,从而得到俯仰角的方程。同样的方法可求得方位角的方程。在算法中,采用初始点多点的滑窗处理方式计算二阶多项式参数。根据所求多项式系数进行预测。其中,初始点为5个点的滑窗处理方式,效果最好。
4 滤波方法比较
卡尔曼滤波为线性时变系统的一种线性无偏最小均方误差估计,它具有时变结构,因此适用于非平稳过程。当先验统计特性一无所知时或在对数据处理精度要求不高或者数据处理量较大的情况下,一般采用最小二乘滤波,最小二乘滤波的优点是运算量小,容易实现。而若知道了动态噪声和观测误差的统计特性则可采用估计精度较高的卡尔曼滤波。卡尔曼滤波具有较强的适应能力,又适于实时处理。因此它优于其他滤波方法。
卡尔曼预测结果如图1所示,最小二乘预测结果如图2所示。

图1 卡尔曼预测结果
其中,卡尔曼预测值与真实值差值的平均值:0.076 493;预测值与真实值差值的最大值:0.874 447;预测值与真实值差值的均方差:0.250 849;而最小二乘法预测值与真实值差值的平均值:0.001 157;预测值与真实值差值的最大值:0.433 086;预测值与真实值差值的均方差:0.016 943。
尽管卡尔曼滤波在理论上是比较完善的,从仿真结果来看将它应用于实际数据的预测,还有很多问题要解决,其中主要是滤波的数学模型、实时能力和数值发散问题。卡尔曼滤波只有在其数学模型确知的条件下才是最佳的。但是在实际预测问题中,要精确建立滤波模型是相当困难的。在滤波模型与实际过程的模型不匹配时,会使滤波精度下降,在本文卡尔曼滤波应用过程中,就误差而言,最小二乘较好。
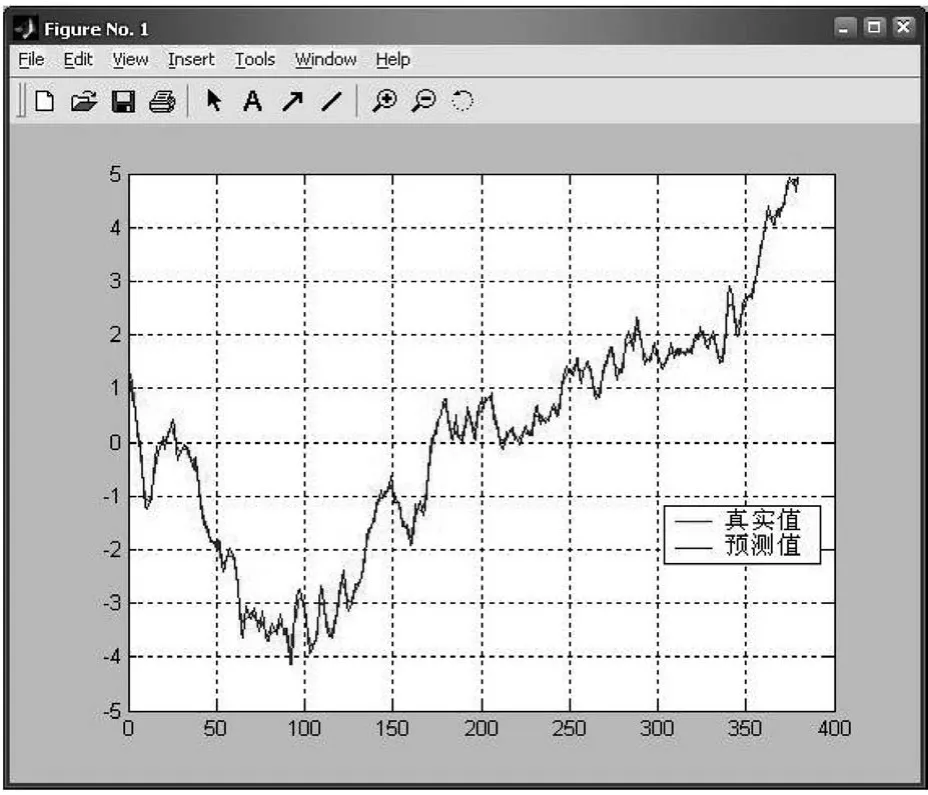
图2 最小二乘预测结果
5 结语
当仿真数据的一些先验统计特性一无所知时采用滑窗处理方式的最小二乘滤波,预测效果较好。而卡尔曼滤波平滑性较好。在进行预测时,上述卡尔曼滤波数学模型还需要进一步改善,首先要根据数据的特性来确定初始状态估计、初始协方差、确定过程噪声和观测噪声的统计特性,这样才能提高卡尔曼滤波的精度。
[1]苗兴国.现代雷达系统的数据处理[J].现代雷达,1980(3):32-47,58.
[2]孙仲康.雷达数据数字处理[M].北京:国防工业出版社,1983.
[3]法里纳,施图德.雷达数据处理[M].匡永胜,译.北京:国防工业出版社,1988.
[4]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2006.
Comparison and simulation of fi ltering algorithm
Yue Haiyan, Yao Hong, Zhou Zunsi
(China Ordnance Equipment Group (Chengdu) Fire Control Technology Center, Chengdu 611731, China)
This paper briefly introduces and compares Kalman fi ltering and the least-square fi ltering algorithm.Two algorithms are used to predict separately, and MATLAB is used to simulate the predicted data.
Kalman fi ltering; least-square fi ltering; predict
岳海燕(1984— ),女,河南濮阳,硕士,工程师;研究方向:软件设计。
