密质骨双裂纹反平面模型问题复变方法研究

郭东升

（宁夏大学 数学统计学院，宁夏 银川 750021）

密质骨双裂纹反平面模型问题复变方法研究

郭东升

（宁夏大学 数学统计学院，宁夏 银川 750021）

文章构建密质骨双裂纹反平面模型，通过复变方法求解了该模型问题，并给出了裂纹尖端处应力及应力强度因子的解析表达式。数值算例分析了骨单元与基质的剪切模量比、裂纹尖端处与骨单元中心的距离和裂纹长度对裂纹尖端应力强度因子的影响。

密质骨；复变方法；裂纹；应力强度因子

密质骨是由矿化胶原纤维螺旋环绕哈弗氏管所构成的自然生物复合材料。Ascenzi等[1-2]最早致力于密质骨微结构的力学性质的研究工作，他们通过实验得到骨单元的弹性模量和强度。张智凌[3]建立包含单个骨单元的骨单元-骨间质两相模型，应用Abaqus扩展有限元分析程序，分析了黏合线对密质骨微裂纹扩展的影响。王旭[4]运用奇异积分方程方法，研究了骨单位密质骨I型裂纹模型平面问题。以上对密质骨材料的研究方法为实验方法和积分方程方法。目前对于密质骨反平面裂纹问题的研究较少。

1 问题陈述

将该骨单元结构模型近似为弹性材料，忽略骨单元之间的相互影响。如图1所示，骨单元周围充满基质，在骨单元两侧附近分别存在一条直线裂纹AB和CD，假设骨单元与基质光滑黏结，基质相对于骨单元和裂纹足够大，在无体积力情况下，该模型在无穷远处受到反平面剪切力的作用。骨单元半径为ρ，骨单元的剪切模量为μi，基质的剪切模量为μm。以骨单元中心建立坐标系，裂纹端点分别设为A(a,0)，B(b,0)，C(-a,0)，D(-c,0)。

图1 密质骨含两条共线径向裂纹的骨单元模型

根据叠加原理，该模型问题可分解为A和B两个问题：问题A为不含骨单元的基质中具有两条共线的径向裂纹且在无穷远处受反平面剪切力的作用；问题B为基质中含有骨单元且在无穷远处不受反平面剪切力的作用。

2 模型求解

密质骨反平面裂纹问题的弹性平衡方程为[5]

3 数值算例

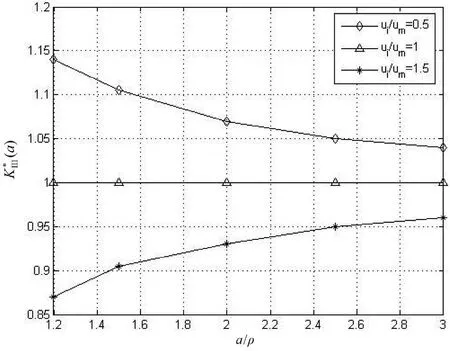
图2 不同剪切比下A端应力强度因子与a/ρ的关系曲线(b-a=10 μm)

图2与图3分别表示裂纹长度为10 μm和20 μm时，不同剪切比下裂纹A端应力强度因子随a/ρ增大的变化曲线。观察图像可得到如下结果。

（1）当骨单元与基质的剪切模量比介于0与1之间时，满足该情形剪切模量比的骨为硬质骨，应力强度因子随a/ρ的增大而减小，且逐渐趋于稳定值。

（2）当骨单元与基质的剪切模量比大于1时，满足该情形剪切模量比的骨为软质骨，应力强度因子随a/ρ的增大而增大，且逐渐趋于稳定值。

（3）当固定裂纹A端增加裂纹长度时，骨单元与基质的剪切模量比介于0与1之间或大于1的情形，曲线的变化趋势与裂纹长度增加前的变化趋势相同，区别在于前者情形增加裂纹长度后对应的应力强度因子的值比之前的小，后者情形增加裂纹长度后对应的应力强度因子的值比之前的大。

4 结语

本文通过复变方法求解了密质骨双裂纹反平面裂纹模型问题，并给出了裂纹尖端A处应力及应力强度因子的解析表达式，数值算例说明裂纹尖端A处的应力强度因子受骨单元与基质的剪切模量比、裂纹尖端A处与骨单元中心的距离和裂纹长度的影响。

图3 不同剪切比下A端应力强度因子与a/ρ的关系曲线(b-a=20μm)

[1]ASCENZΙA E.Bonucci.The tensile properties of single osteons[J].The Anatom ical Record，1967（4）：375-386.

[2]ASCENZΙ E, BONUCCΙ. The compressive properties of single osteons[J].The Anatom ical Record，1968（3）：377-391.

[3]张智凌.密质骨多级微结构的强韧机理[D].重庆：重庆大学，2014．

[4]王旭.密质骨含微裂纹问题奇异积分方程方法[D].宁夏：宁夏大学，2011．

[5]刘又文，蒋持平.反平面集中力作用下不同材料界面共线裂纹问题[J].应用数学和力学，1900（10）：893-902.

[6]MUSKHELΙSHVΙLΙ N Ι. Some basic problems of the mathematical theory of elasticity[M]. USA：Springer Science & Business Media，1997.

Research on complex method for inverse problem of BΙ plane crack model of compact bone

Guo Dongsheng
（Mathematics and Statistics School of Ningxia University, Yinchuan 750021, China）

Ιn this paper, the model of the double plane crack of the dense bone is constructed, and the model problem is solved by the complex method, stress at crack tip and the analytic expression of stress intensity factor is given. Numerical example analyzes the influences shear modulus ratio of bone unit to stroma, the distance between the crack tip and the center of bone unit center, and influence the crack tip stress intensity factor on crack tip stress factor.

compact bone; complex method; crack; stress intensity factor

郭东升（1987— ），男，安徽宿州，硕士，研究方向：复分析在力学中的应用。