一种基于最长路径的脉冲序列抽取算法
2017-06-19苏焕程陈昌云程亦涵
苏焕程,张 君,陈昌云,程亦涵
(中国航天科工集团8511研究所,江苏 南京 210007)
一种基于最长路径的脉冲序列抽取算法
苏焕程,张 君,陈昌云,程亦涵
(中国航天科工集团8511研究所,江苏 南京 210007)
针对传统的动态关联算法在脉冲序列抽取方面存在的不足,提出了一种基于最长路径原理的脉冲序列抽取算法。该算法首先将待抽取的脉冲序列转换为一个经过拓扑排序的有向无环图,然后求解该有向无环图的最长路径,最后根据该最长路径抽取出相应的脉冲序列。相比较于传统的动态关联算法,基于最长路径的算法性能受设置的容差大小的影响较小,可以有效地提高脉冲序列抽取的正确率,并且具有较高的稳定性,从而能够更好地满足信号分选算法的实际工程需要。仿真实验表明了该算法的有效性。
信号分选;序列抽取;有向无环图;最长路径
0 引言
雷达截获系统的作用是截获一定频域和空域范围内的雷达辐射源信号并确定其特征。如何在密集的电磁环境中正确地分离出各部雷达辐射源信息,得到正确的参数,实时地识别、告警,正确引导反辐射导弹进行攻击或干扰系统进行干扰已变得越来越重要。而信号分选在雷达截获系统设备中是重要的组成部分之一,信号分选的正确与否直接关系到设备的性能指标。从目前的信号分选技术来看,一般将信号分选分为两级处理,首先根据到达方向(DOA)、载频(RF)等参数对雷达信号进行预分选,再利用脉冲重复间隔(PRI)对信号做进一步的分选[1]。
传统的PRI分选算法的处理过程可分为PRI估计和脉冲序列抽取两部分[2],即先通过PRI估计得到一个可能的雷达辐射源PRI,再以该可能的PRI数值为参考对脉冲序列进行抽取,从而实现对雷达辐射源脉冲的分选。目前的研究重点基本都集中在对PRI的快速、准确估计上,这是由于准确的PRI可以提高脉冲抽取的准确率。然而在复杂电磁环境下,大量的脉冲互相交错,想要准确地估计出雷达辐射源的PRI是非常困难的,并且由于TOA测量精度偏差较大,即使是估计出准确的PRI也难以保证脉冲序列抽取的准确率。相比较于不断出现的各种PRI估计算法,对脉冲序列抽取技术的研究相对较少,基本都集中在动态关联算法及其改进算法上。而动态关联算法虽然在简单环境下具有较高的性能,但是在复杂电磁环境下受所选择的PRI窗口大小影响较大,一旦发生抽取错误可能导致后续抽取均错误,性能波动较大。
为了克服动态关联算法的缺陷,本文提出了一种基于最长路径的脉冲序列抽取算法。该算法首先将待抽取的脉冲序列转换为一个拓扑排序的有向无环图,然后求解该有向无环图的最长路径,最后根据该最长路径抽取出相应的脉冲序列。相比较于传统的动态关联算法,该算法的性能受PRI窗口大小的影响较小,可以有效地提高脉冲序列抽取的准确性,并且具有较高的稳定性,从而能够更好地满足信号分选算法的实际需求。仿真实验表明了该算法的有效性。
1 动态关联法描述
动态关联法又称为扩展关联法或PRI窗口预置法[3-4],其基本工作原理是:先按一定规则形成准PRI,然后利用准PRI对脉冲序列进行关联匹配,完成对脉冲序列的抽取。算法步骤大致可分为:
Step1 形成准PRI:采用任意一种PRI估计算法得到一个可能的雷达辐射源PRI作为准PRI。
Step2 搜索基准对:在脉冲流内选择两个脉冲间隔等于准PRI(容差范围内)的脉冲对,以这两个脉冲对作为基准脉冲对,通常称脉冲对的第一个脉冲为基准脉冲,第二个脉冲为参考脉冲。
Step3 产生预置窗口:预置窗口的中心为参考脉冲的TOA加上准PRI,预置窗口的宽度根据脉冲的抖动、TOA测量误差等因素确定。
Step4 移动预置窗口:若没有脉冲落入预置窗口内,则将窗口的中心向右移动一个准PRI的时间长度;如果在规定的移动次数内均无脉冲落入预置窗口内,或预置窗口超出了最后一个脉冲的TOA则结束动态关联算法,并输出抽取成功的脉冲。
Step5 提取脉冲序列:对于落入预置窗口内的脉冲,根据一定的准则提取其中一个脉冲,并将该脉冲作为新的参考脉冲,同时转到Step3。
动态关联法的脉冲抽取过程如图1所示,以第一个参考脉冲开始生成预置窗口,根据选择的窗口内脉冲作为新的参考脉冲再不断地生成新的预置窗口,并不断地进行窗口内脉冲抽取。
在动态关联法的脉冲抽取过程中,预置窗口宽度的选择非常重要,窗口选得较窄可以更准确地抽取到正确的脉冲,但实际雷达脉冲总存在抖动,TOA测量总存在误差,窗口窄了就会漏失脉冲;窗口选得较宽就可以减少漏失,但是在信号密集环境下会同时有多个脉冲落入窗口内,在没有其他可靠参考因素的条件下,通常会造成错选。无论是脉冲的漏失或错选,都会导致下一次产生的预置窗口的准确性下降,导致漏失或错选的概率进一步的增加,如图2所示。
在图2中,由于真实的雷达脉冲丢失,动态关联算法错误地抽取了编号为7的干扰脉冲,结果导致后续的脉冲抽取全部发生错误。
通过上面的分析可知,动态关联法对所选择的预置窗口的宽度非常敏感,算法稳定性较差,一旦发生脉冲漏失或错选就会造成更严重的漏失或错选。
2 基于最长路径的脉冲序列抽取算法
2.1 最长路径理论
对于给定的图G=(V,E,W),V是节点集合;E是边的集合,是二元关系V×V的子集;W是权值的集合,是E上的实值函数W:E→R。若E是无序的二元关系集合,则称图G是无向图;若E是有序的二元关系集合,则称图G是有向图,若图G中不存在回路,则称图G是有向无环图[5]。
在图论中,图的最长路径(Longest path)问题就是在图中寻找一条无回路的最长路径的问题。对于无权图,是求解一条经过边数最多的路径;而对于有权图,是求解一条权值最大的路径。
在无向图中求解最长路径问题是著名的NP难题,但是在有向图中求解最长路径却存在着多项式时间内的算法[6]。文献[7~8]分别在区间图(Interval Graphs)、共相似图(CoComparability Graphs)中,根据图中节点的次序关系采用动态规划的策略在多项式时间内求解最长路径问题。
文献[5]提出了一种将带权值的有向无环图进行拓扑排序,然后求解最大路径的算法。有向无环图的拓扑排序是指将有向无环图的所有节点排成一个线性序列,若图中有边(u,v)∈E,则在最终的排序结果中,节点u总排在节点v的前面。图3是一个有向无环图的实例,经过上述的拓扑排序后得到如图4所示的一个线性序列:S、C、A、B、D、E。
如图4所示,拓扑排序得到了节点的一个线性排序,且源点S到节点E的最大路径是建立在S到节点B和S到节点D的基础上。这表示在求解源点到后面节点的最长路径时,根据有向边之间的连接关系,可以参照前面已经求得最大路径值的节点。这意味着如果按照线性序列来求解最长路径,源点到节点间的最长路径满足最优子结构:源点到节点的最大路径中的任意节点的路径也是最大的。因此可以采用动态规划的方法求解最大路径问题[5]。
如果将有向无环图所有边的权值均设置为相等的值,则对带权值的向无环图求解最大路径等效于对无权值的有向无环图求解最长路径。
2.2 脉冲序列抽取分析
下面采用有向无环图的相关理论,对基于动态关联法的脉冲序列抽取过程进行分析。
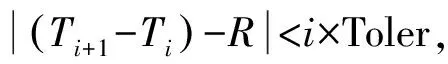
由于脉冲序列是按照TOA顺序排列的,所以如果上述转换过程中严格按照各个节点对应TOA的顺序产生相应的有向边,则可以直接得到经过拓扑排序后的有向无环图,省去了拓扑排序过程。图4是一个脉冲序列的转换实例,其中门限M=2。
如图5所示,如果脉冲3落在脉冲1形成的预置窗口内,则等效于在有向无环图中节点1和节点3之间存在一条节点1到节点3的有向边。故采用动态关联法的脉冲抽取过程等效于在有向无环图中从节点1找一条到节点12的路径,而在该条路径上的每一个节点等效于抽取得到的脉冲。
综上所述,通过采用有向无环图模型,可将基于动态关联法的脉冲序列抽取过程转换为在有向无环图中搜索两个节点之间路径的问题。
2.3 脉冲序列抽取算法
通过对大量实际侦测到的脉冲序列深入分析可知,除干扰脉冲外,脉冲序列中其余的每一个脉冲都对应于某一部雷达,并以某一脉冲作为参考脉冲,其对应雷达的帧周期作为准PRI在时间上向前(或向后)进行抽取时,可以抽取到的脉冲个数多于以其它准PRI抽取得到的脉冲个数[7]。
反之,如果采用动态关联法进行脉冲抽取,则最优的抽取结果应当可以保证最终抽取得到的脉冲数最多。根据该分析,在采用动态关联法进行抽取时,落在预置窗口内的多个脉冲中能够保证以该脉冲为参考脉冲继续进行抽取,最终抽取得到的脉冲数最多的那个脉冲就是正确脉冲的概率是最大的。
魏乐村:斗渠长度由2 170 m变为2 605 m,比原设计增加435 m,1-1农渠长度由850 m变为1 300 m,1-2农渠长度由820 m变为700 m,1-3农渠长度由930 m变为1 700 m,1-4农渠长度由980 m变为2 410 m,1-5农渠长度由990 m变为1 200 m,变更后农渠总长比原设计增加2 740 m。
在上节中,本文已经通过有向无环图对基于动态关联法的脉冲序列抽取过程进行描述。故对于脉冲序列的最多脉冲数抽取问题即可转换为在相应的有向无环图中求解最长路径的问题。根据以上分析,可以给出基于最长路径的脉冲序列抽取处理流程:
Step1 形成准PRI:采用任意一种PRI估计算法得到一个可能的雷达辐射源PRI作为准PRI。
Step2 序列转换:根据2.2节提供的方法,将待抽取的脉冲序列转换为一个拓扑排序的有向无环图。
Step3 窗口形成:将有向无环图首节点设置为起点,以起点为基准形成N个预置窗口,预置窗口的宽度根据容差设置,预置窗口的中心分别为起点对应脉冲的TOA加上i×准PRI数值(i=1,2,3,…,N),应当保证第N个窗口的中心点大于脉冲序列最后一个脉冲的TOA数值,如图6所示。
Step4 终点设置:从第N个预置窗口开始搜索,如果预置窗口内存在脉冲,则选择与窗口中心点最近的脉冲并设置为终点,转到Step5;否则搜索第N-1个预置窗口,依次类推。
Step5 路径搜索:采用文献[5]的算法,从有向无环图起点开始,搜索到终点之间的最长路径,如果搜索成功则输出对应的脉冲,否则删除有向无环图的首节点,将第2个节点设置为首节点并转到Step3。
如图6所示,根据首节点形成了多个预置窗口,并根据形成的预置窗口确定相应的终点。
3 仿真实验
为了验证基于最长路径的脉冲序列抽取算法的有效性和算法的稳定性,本文进行了以下实验。
实验1:仿真信号源为5部PRI固定的雷达辐射源,PRI在50μs~50ms之间随机,TOA测量误差小于100ns,脉冲丢失率小于5%。分别采用传统的动态关联法以及最长路径法进行脉冲序列抽取,共测试了100组数据。抽取时的容差设置为500ns,即PRI预置窗口宽度为1μs,仿真结果见表1。
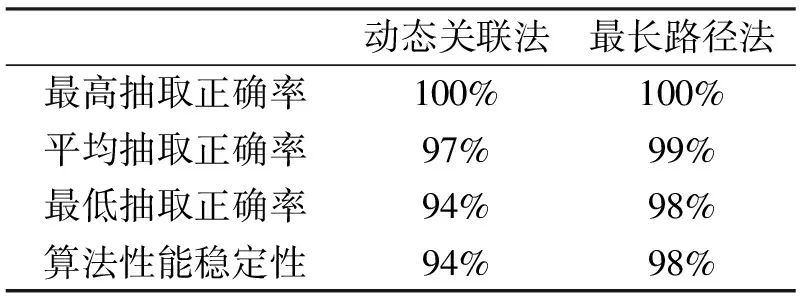
表1 抽取算法性能比较(简单环境)
从表1仿真结果可以得出,在信号环境较为简单且测量精度较高的条件下,两种算法的抽取正确率和性能稳定性均较高,算法性能差异较小。
实验2:设置仿真信号源为20部PRI固定的雷达辐射源,PRI在50μs~50ms之间随机,TOA测量误差小于1μs,脉冲丢失率小于30%。分别采用传统的动态关联法以及最长路径法进行脉冲抽取,共测试了100组数据。抽取时的容差设置为500ns,即PRI预置窗口宽度为1μs,仿真结果见表2。
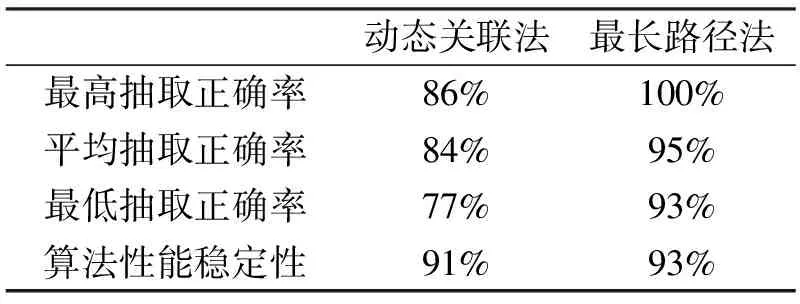
表2 抽取算法性能比较(复杂环境)
从表2仿真结果可以得出,在信号环境较为复杂且测量精度较差的条件下,动态关联法的抽取正确率明显低于最长路径法。
实验3:设置仿真信号源为5部PRI固定的雷达辐射源,PRI在50μs~50ms之间随机,TOA测量误差小于100ns,脉冲丢失率小于5%。分别采用传统的动态关联法以及最长路径法进行脉冲抽取,共测试了100组数据。抽取时的容差设置为5μs,对应预置窗口宽度为10μs,仿真结果见表3。
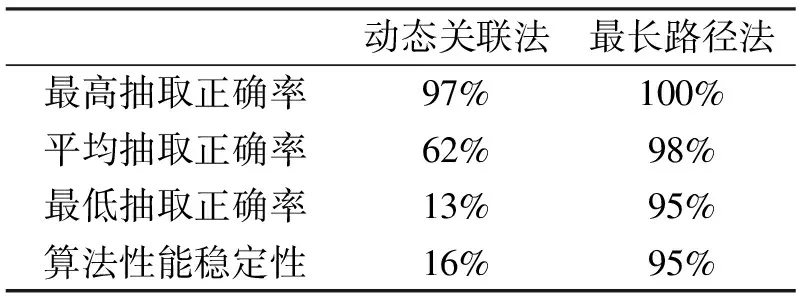
表3 抽取算法性能比较(5μs容差)
从表3仿真结果可以得出,在与实验1同样的仿真环境,增大了抽取容差后,动态关联法的稳定性发生了较大的下降,而最长路径法基本没有变化。
实验4:设置仿真信号源为5部PRI固定的雷达辐射源,PRI在50μs~50ms之间随机,TOA测量误差小于100ns,脉冲丢失率小于5%。分别采用传统的动态关联法以及最长路径法进行脉冲抽取,共测试了100组数据。抽取时的容差设置为50ns,对应预置窗口宽度为100ns,仿真结果见表4。

表4 抽取算法性能比较(50ns容差)
从表4仿真结果可以得出,在与实验1同样的仿真环境下,通过减小抽取容差,动态关联法的抽取正确率和算法性能稳定性均发生了明显的下降,而最长路径法的抽取正确率均虽然也发生了下降,但是算法性能仍然保持较为稳定。
通过对实验1~4的仿真结果进行分析,可得出结论:在复杂环境或测量精度较低的情况下,动态关联算法的抽取正确率明显低于最长路径法。当对抽取的容差进行调整后,动态关联算法的抽取正确率发生较大波动,而最长路径法的算法性能较为稳定。这是由于动态关联算法对抽取错误的敏感度较强,一旦发生脉冲抽取就会影响到下一次的抽取,甚至导致后续的抽取全部错误,而最长路径法则具有较强的自我“纠错”能力,一旦抽取到错误的脉冲,导致后续可抽取脉冲数减少,算法就会回到抽取错误的位置重新进行脉冲抽取,保证算法最终抽取到的脉冲数最多。
4 结束语
本文提出了一种基于最长路径的脉冲序列抽取算法,该算法能够克服传统关联比较法的不足,受算法容差影响较小,可以有效地提高脉冲序列抽取的正确率,且具有较高的稳定性,能够更好地满足信号分选算法的实际需求。但是,该算法也具有自身的局限性,即该算法所要求的计算量相对较大,算法的实时性还有待进一步优化和提升。■
[1] 杨文华, 高梅国. 基于PRI的雷达脉冲序列分选方法[J].现代雷达, 2005, 27(3):50-59.
[2] 关一夫,张国毅,刘志鹏. 一种基于脉冲样本序列的PRI 周期信号分选算法[J]. 电讯技术,2014,54(7):915-920.
[3] 朱红亮. 脉冲重频分选算法的研究[D]. 西安:西安电子科技大学, 2010.
[4] 何炜. 雷达信号分选关键算法研究[D]. 成都:电子科技大学,2007.
[5] 尤磊, 符利勇, 宋新宇. 最大路径算法在原条量材优化中的应用及其优化[J]. 信阳师范学院学报,2014,27(4):605-624.
[6] Sedgewick R,Wayne K. Algorithms [M]. 4th ed. Pearson Education, 2011.
[7] Ioannidou K,Mertzios GB,Nikolopoulos SD. The longest path problem has a polynomial solution on interval graphs[J]. Algorithmica,2011, 61(2):320-341.
[8] Mertzios GB,Corneil DG. A simple polynomial algorithm for the longest path problem on cocomparability graphs[J]. SIAM Journal on Discrete Mathematics,2012, 26(3):940-963.
[9] 李英达,肖立志.一种脉冲重复间隔复杂调制雷达信号分选方法[J]. 电子与信息学报, 2013, 35(10):2493-2497.
An algorithm of extracting pulse sequence based on longest path
Su Huancheng, Zhang Jun, Chen Changyun, Cheng Yihan
(No.8511 Research Institute of CASIC, Nanjing 210007, Jiangsu, China)
For the defects in pulses sequence drawing out of traditional dynamic association algorithm, a new algorithm of pulses sequence drawing out based on longest path is put forward. The algorithm firstly transforms the pulses sequence to directed acyclic graph which topological sorted, then searches the longest path, extracting the pulse sequence based on the longest path at last. Compared with the traditional dynamic association algorithm, the performance of this algorithm is not fluctuate on toler vary, and increase the pulse extracting accurate rate, which satisfies the requirement of the signal sorting process. Simulation results verify the validity of the proposed algorithm.
signal sorting; pulse extracting; directed acyclic graph; longest path
2017-01-11;2017-03-06修回。
苏焕程(1983-),男,高工,主要研究方向为电子对抗信息处理。
TJ76;TN972
A
