对PM2.5的每日变化进行近似函数分析的数学建模

傅孔华

（浙江省宁波市镇海区龙赛中学）

摘 要：从某段时间开始，大家每天讨论的话题是空气质量，PM2.5爆表，以及随之带来的空气净化器效应，这些都是非常时髦的话题。浅层次地研究PM2.5的每日变化规律，然后建立一个近似的数学模型，从而更好地清楚PM2.5的每日变化规律，这样，就知道何时去锻炼比较合适，怎样外出有利于身体健康。

关键词：PM2.5；数学；近似分析；二次函数；反比例函数

我们先来了解一下PM，即 particulate matter（颗粒物）。PM2.5是指空气中有一些颗粒物的半径小于或等于2.5微米，由于它细小，所以在空气中能够悬浮较长时间。而且根据研究表明，PM2.5在空气中含量浓度越高，那么当地的空气污染越严重。如果用每立方米PM2.5在空气中颗粒的含量（微克/立方米）表示污染程度，那么，空气污染程度与这个值成正比。

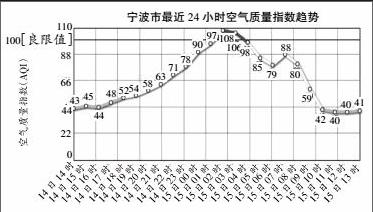
有关PM2.5的数据由于无法自己检测，所以文章中引用了宁波市和杭州市PM2.5检测网站上得到的数据和图片，以此来建立有关近似函数分析的数学模型。以下是从宁波市PM2.5检测网站上得到的数据和图片，以此来进行分析。

经过数据对比，以及国家公布的PM2.5检测网空气質量标准：24小时平均值标准值分布如下：优为0-35，良为35-75，轻度污染为75-115，中度污染为115-150，重度污染为150-250，严重污染：大于250（单位为ug/m3）。

一、几类函数模型及其增长差异

（1）几类函数模型：一次函数模型、反比例函数模型、二次函数模型、指数函数模型、对数函数模型、幂函数模型。

（2）三种函数模型的性质，让学生合作学习，研究一下性质：单调性、奇偶性、定义域、值域等。

这个过程由学生参与、讨论分析，最终的结论也是由学生获得。整个研究过程包括画图、计算。由学生下结论是本节课的重点过程，可以利用启发式教学策略，激发学生的求知欲和表演欲，从而展现课堂的活力。

学生一定对结论非常感兴趣，有些学生猜测是二次函数；有些学生猜测是反比例函数；有些学生猜测是指数函数甚至是对数函数；有些学生猜测是二次函数与反比例函数结合。

这时，我要告诉学生的是，生活中的数学是非常复杂的，我们只能近似地得到函数模型，是不可能很准确地得到PM的准确函数的，这就是数学与生活的区别。但是，我们学好了数学中的常见工具，并将其应用到生活中去，这就是我们学习数学的意义。

经过学生的投票，大部分学生认可了通过二次函数和反比例函数结合得到PM2.5的近似图像。

二、高中生解决函数应用问题的黄金步骤

1.关键在于读题

当不明白题意时，要反复读题。分清条件和结论，目标是什么，条件又翻译到什么程度，最后选择合适的数学模型。

2.建立合适的数学模型

大脑中必须储存一定量的常见数学模型，从大脑中提取，而不是每次都是凭空想象，这样会增加做题的难度。

3.解决数学模型

建立好数学模型之后，我们必须要解决它。但是一定要注意，实际问题不一定只有唯一的答案，也不一定有答案。

4.还原

将数学问题还原为生活问题，这是对数学的反思，也是对生活的深层次解读。要注意实际问题的自变量的取值范围，合理确定函数的定义域。

通过今天这节课，大家知晓了PM2.5的每日的大致变化规律，可以通过二次函数和反比例函数结合得到。这样，我们就知道何时去锻炼比较合适，也可以建议学校什么时候去跑操。

生活中，数学是非常复杂的，我们只能近似地得到函数模型，是不可能很准确地得到PM的准确函数的，这就是数学与生活的区别。生活中的数学，往往不是精确的，是需要我们学习更多的知识，精益求精，用更好的函数来描述某种现象。这就要求我们每一个热爱数学的人孜孜不倦，精益求精。

参考文献：

张宇烽.PM2.5和PM10监测数据“倒挂”成因浅析[J].广东化工，2013（12）.

编辑 高 琼endprint