关于振动时效的振动力学分析探讨

杜佩明+何尚文

摘 要 工程材料在加工过程中存在残余应力，振动时效便是削减残余应力的一种方法。它通过外加振动使其与工件内部残余的内应力矢量和超过材料屈服强度，利用材料发生的微量塑性变形来减轻材料内部的内应力。本文从材料内部的残余应力出发到外加激振力对振动时效进行振动力学的分析和讨论，对振动时效工艺的选择有一定的参考价值。

关键词 振动时效；振动力学；分量

中图分类号 G3 文献标识码 A 文章编号 2095-6363（2017）06-0004-02

振动时效英文缩写为VSR，由于本身具有其他相关工艺技术没有的综合性优势，因此被广泛应用于相关的工业行业领域。首先是在铸造构件上得以应用，之后普及到低碳钢材料焊接件，再到目前较为先进的合金钢结构、不锈钢结构以及其他金属的合金材料，在其锻造与构件的焊接过程中都得到了成功的使用。振动时效在应用的过程中具有明显的综合效果。所以振动力学分析需要明确工艺理论以及构建疲劳状态，针对结构复杂性特点分析残存应力作用，同时能够对刚度分布状况形成大致了解。通过不同应力作用下的微观塑性能够对振动进行一定的分析。

1 振动时效中的残余应力

构件承受荷载时，由于残余应力的存在，荷载引起的应力将与截面残余应力叠加，使构件某些部位提前达到屈服强度并产生塑性变形。然而如果继续增加荷载，只有截面弹性区承受增加的荷载，塑性区的应力不再增加。所以，残余应力不影响构件强度。但由于产生了塑性变形，故构件的刚度和稳定性将有所降低，同时将降低其抗冲击断裂和抗疲劳破坏的能力。此外，理论和实验研究表明构件内残余应力的存在，对构件的固有频率、阻尼等参数将产生影响[ 1- 3 ]。原机械部颁发的振动时效工艺参数选择及技术要求中规定，当振幅频率曲线出现振后的峰值点，即可判定为出现了振动时效效果[4]，由此推断出振动时效过程中构件固有频率发生了变化。

2 振动时效中的屈服极限

振动时效理论在进行均化和减弱结构构件上的残余应力时，常常会使用共振动应力和构件残余应力相加大于构件屈服应力极限的公式。一般情况下，发生共振情况的材料构件上的某一个区域都会产生动应力和残余应力的叠加，如果大于屈服极限的不等式成立，那么构件会由于形变的原因促进构件本身残余应力的释放，但若把不等式中的屈服极限看作基本概念层面的理解，那么这个等式显然是忽视了构件应变效率后得出的结果。由材料力学的相关知识知道，不同材料构件的屈服极限和应力的瞬时值并非一成不变，而会随着材料应变效率的增加而增加，这就是振动时效下产生的应变效率反应。即振动时效中的屈服极限有着动态和静态的区别，而理论中的屈服极限往往指的是静态，因此这种方法不适用于加载速度变化较大的构件。

3 振动频率的选择

振动时效技术是在外加激振力的响应下实现消除内部残余应力的，这就要考虑激振频率的选择。由上面的内容得知残余应力对固有频率也会产生一定的影响，所以对振动频率的讨论显得便尤为重要了。振动时效的工作系统是在共振的状态下工作的。即要求阻尼比γ=ω/ωn值为1，其中ω为外激振频率，ωn为构件固有频率，可由振动力学的相关知识求解到。由图1中可以看出共振时，可用较小的外激力产生较大的振幅和动应力。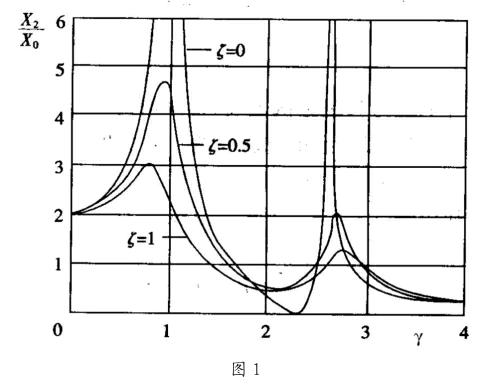

所以此时消除残余应力效果也比较好。但由于一个多自由度系统有多个固有频率，所以使系统共振时有多个自由度可供选择。但最终的激振频率的选择要以残余应力的分布状态为依据，并要考虑结构的振型[5]。

4 振动时效中的激振力和激振时间

振动时效中的激振力来源于偏心转子在电机中产生的离心力F。其值可由下面的公式计算： F=（Q/g）ω2rsin（ωt）

F—激振力（kN）；Q—偏心环重（N）；

g—重力加速度；ω—角速度；r—偏心距（mm）而激振时间是以振动系统参数的宏观特征变化来确定的。不能简单地认为只要使动应力和残余应力矢量和大于材料的屈服强度就可以达到技术要求。对于激振时间的确定，可由振动力学的相关知识可知在确定了共振频率之后，可计算出此时系统的振动周期Td作為参考。计算公式如下：

Td=2π/ωd；ωd=/ωn（1-ζ2）？；ζ=c/2mωd

C-粘性阻尼系数；ζ-阻尼比；m-质量；ωn-固有频率。

5 关于振动时效中振动力学的一些思考

1）由于工程中的构件多为多自由度系统，考虑到多自由度系统在共振时的局部性，即在外激力的作用下有多个共振峰，每次只能消除材料中局部的残余应力，故需要多次加载，在多个共振峰振型的叠加下，最终实现构件内部残余应力的消除。例如悬臂梁在收到外激力时会发生多阶共振，而不同的振型导致梁的变形也不同，所以不同频率的外激力下产生不同的响应，对残余应力的消除也有不同效果。

2）振动时效技术应用为其微观和理论机理的深入研究奠定了基础。该技术使用的对象往往是结构组成都较为复杂的构件，而且在实践过程中产生的应力和刚度变化的范围也比较大，加上共振时发生的激振力逐渐循环提高，构件上的振动波也会随之在多个方向和自由度上进行传播，也会导致材料发生一定程度的形变，这一系列的过程也是振动时效理论区别于一般振动分析的地方。

6 结论

综上所开展振动时效和振动力学的研究，不仅能为机械振动的经典理论加以诠释，还能提出新颖的观点推动现有振动时效相关课题的研究进程。

参考文献

[1]高永毅，苏志宵，焦群英，等.残余应力对构件固有频率影响的讨论[J].机械强度，2002，24（2）：289-292.

[2]高永毅，刘德顺.利用试验模态分析进行残余应力评估的研究[J].振动与冲击，2005，24（5）：111-114.

[3]李文威，董学武，王东强，等.铸铁构件固有频率与其残余应力关系的研究[J].中原工学院学报，2007，18（2）：7-10.

[4]胡永会，吴运新.振动时效中残余应力与固有频率的相互作用[J].材料研究与应用，2012，6（1）：14-20.

[5]高葛，张锁怀.对振动时效三个主要参数的探讨[J].工艺与工艺装备，2004（5）：58-60.