“错”中思因

陆丽萍

“错”中思因

陆丽萍

一、概念不清

例1下列哪些是二元一次方程组？

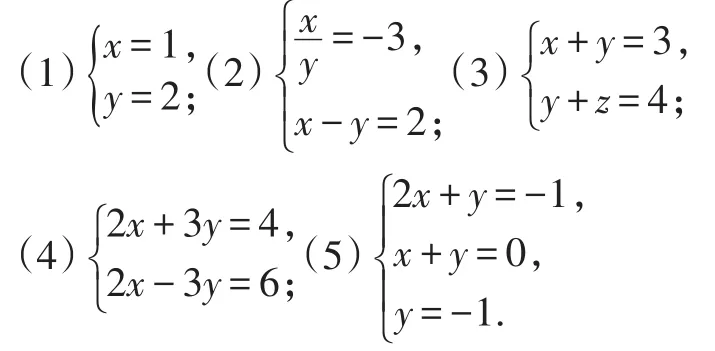
错解：（3）、（4）.

剖析：二元一次方程组应从三个方面来理解：①未知项最高次数是1的整式方程；②方程组总共只有两个未知数；③方程的个数可以多于2个.

正解：（1）、（4）、（5）是二元一次方程组.

二、解法错误

例2解方程组：

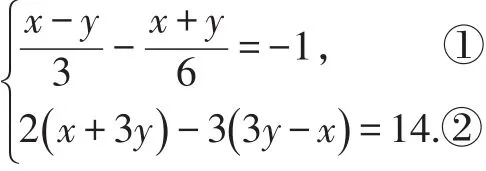
错解一：①×6得：2（x-y）-（x+y）=-1.

剖析：去分母时漏乘不含分母的项.

错解二：②×6得：2x-2y-x+y=-6.

剖析：忽略分数线的括号作用.

错解三：由③得：2x+6y-9y-3x=14.

剖析：忘了括号前的负号和乘法分配律.

正解：①×6得：2（x-y）-（x+y）=-6，化简得：x-3y=-6.③

②变形得：2x+6y-9y+3x=14，化简得：5x-3y=14.④

三、考虑不全面

有整数解，x、y均为整数，求2017-m的值.

错解：①+②得：（m+3）x=10，∴x=1，m=7，则2017-m=2010；或者x=2，m=2，则2017-m= 2015.

剖析：没考虑y也是整数.

正解：①+②得：（m+3）x=10.

若x=1，m=7，此时y=1.5（舍去）.

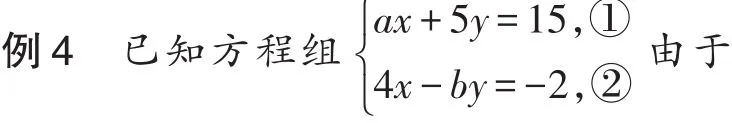
若x=2，m=2，此时y=3，则2017-m=2015.甲看错了方程①中的a得到方程组的解为乙看错了方程②中的b得到方程组的若按正确的a、b计算，求解方

剖析：很多同学没有弄懂题目意思，甲看错a，没看错b，得到的解应该满足方程②，同理乙看错b，没看错a，得到的解应该满足方程①，分别代入，即可求得答案.

（作者单位：江苏省盐城市初级中学）