抓住方程精髓放飞数学思想

仇玉海

抓住方程精髓放飞数学思想

仇玉海

在初中数学的学习过程中,同学们不仅需要掌握各种各样精彩的解题方法,而且还要能把方法归纳为数学思想,明晰数学知识之间的脉络和联系，由此才能熟练掌握教材中所隐藏的数学解题技巧和思想方法.下面，我们举例说说解二元一次方程组中的数学思想方法.

一、转化思想

二元一次方程组的解法的实质就是借助“消元”（加减消元和代入消元是两种最常见的消元方法）的方法将“二元”转化为“一元”.“转化”思想就是将复杂的、陌生的问题迁移为简单的、熟悉的问题进行求解，这是学习新知识、研究新问题的一种基本方法.

【点评】本题运用了转化的思想.第一，根据同类项的定义，将求解m、n的问题转化为解关于m、n的二元一次方程组的问题；第二，运用“消元”的方法，将解二元一次方程组问题转化为解一元一次方程问题.当然本题还运用了方程的思想.

二、整体思想

整体思想，就是在研究和解决有关数学问题时，通过研究问题的整体形式、整体结构、整体特征，对问题进行整体处理的解题方法.从整体上去认识问题、思考问题，常常能化繁为简、变难为易，同时又能培养同学们思维的灵活性、敏捷性.

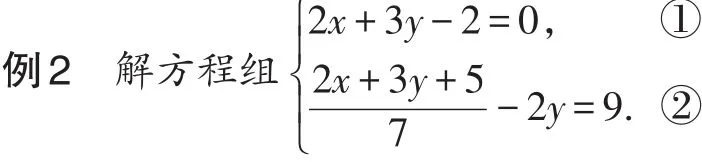
【分析】方程①②中均含有2x+3y，可用整体思想求解.

由①得2x+3y=2，③

再把y=-4代入①，得x=7，

【点评】我们在解题过程中经常使用整体思想，整体思想使用得恰当，能提高解题效率和能力，减少不必要的计算，少走弯路.

三、换元思想

换元法在初中代数中的应用非常广泛，它通过用一个字母表示一个整体进行变量替换，将形式简化，从而达到化繁为简，化隐为显，化难为易的目的.

【分析】把方程组中的x+y与x-y进行整体换元，简化方程组.

由①+②×9得17u=68，u=4.将u=4代入②中得v=2.∴

【点评】本题借助换元的方法，将复杂的方程组转化为简单的方程组来解决.

（作者单位：江苏省盐城市初级中学）