利用方程思想解决几何问题
2017-06-15潘霞
潘 霞
利用方程思想解决几何问题
潘 霞
著名的数学家笛卡尔在《思维的法则》中提出过一个解决各种问题的“万能方法”:任何问题→数学问题→代数问题→方程求解.方程思想被广泛应用,内涵丰富,是研究数量关系的重要工具.用方程思想解决几何问题,我们要先设未知数,用未知数表示已知量,再通过分析题目中蕴含的等量关系,利用所学的定理、性质等找出等量关系,用方程的形式将其表示出来,从而实现用方程有效地解决几何问题的目的.
一、列方程求角的度数
例1(母子等腰三角形)如图1,在△ABC中,AB=AC,点D在AC上,AD=BD=BC,求∠A的度数.
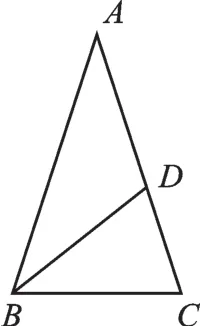
图1
【分析】求角的度数,但题目条件中没有出现任何一个角的度数,那么就需要根据边相等得到角之间的关系,如果我们设∠A的度数为x,则图中其余各角用含x的代数式在图中标出,根据三角形内角和为180°列出方程,从而求得∠A的度数.
解:如图1,设∠A的度数为x,
∵AD=BD,∴∠ABD=x,
∴∠BDC=∠A+∠ABD=2x.
∵BD=BC,∴∠C=2x.
∵AB=AC,∴∠ABC=2x.
∵在△ABC中,∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°,∴x=36°,即∠A=36°.
【点评】等腰三角形中求某个角的度数时,通常都可以根据“三角形内角和公式、外角的性质、等腰三角形的性质”等找到等量关系,列出方程解决.
二、列方程求线段的长度
例2(母子直角三角形)如图2,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=3,BC=4,求CD的长.
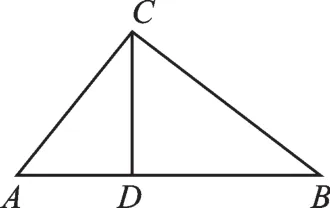
图2
【分析】母子直角三角形,大家非常熟悉,首先利用勾股定理求出AB的长为5.
方法一:等面积法列方程,利用不同方法表示Rt△ABC的面积,建立方程:5×CD=×3×4,求出CD的长.
方法二:勾股定理列方程,将Rt△ACD和Rt△BCD的公共线段CD分别放在两个直角三角形中,设AD=x,则BD=5-x,利用勾股定理表示CD2,建立方程:32-x2=42-(5-x)2,求出CD的长.
方法三:根据相似图形对应线段成比例列方程,由△ACD∽△ABC,得到,建立方程:,求出CD的长.
方法四:根据相等角的三角函数相等,也可以建立方程,将∠A分别放在△ACD、△ABC中,其正弦值相等,得到,建立方程:,求出CD的长.
【思考】你会几种方法解这道题?你觉得哪种方法比较简便?尝试从不同角度去认识这个基本图形,当然方法优化很重要.
三、中考试题掠影
例3(2014·郴州)如图3,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则BE的长为 .
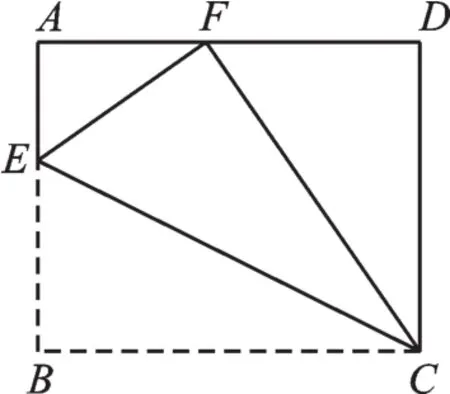
图3
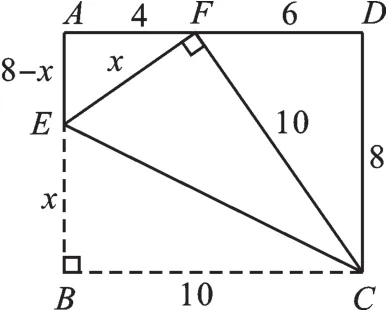
图4
【分析】这是折叠问题,根据折叠性质,得到一些相等的线段、相等的角,同学们可以试着在图上把能表示的线段、角标出来.CF=BC= 10,CD=8,易得DF=6,AF=4,如果设BE=x,则EF=x,AE=8-x,∠EFC=∠B=90°,如图4.
方法一:在Rt△AEF中,利用勾股定理可建立方程:42+(8-x)2=x2,即可求出BE的长.
【点评】善于找到题目中隐含的等量关系是关键,通常我们根据勾股定理、相似三角形对应线段成比例、面积、三角函数等来建立方程.
例4(2015·威海)如图5,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE= 3,求AC的长.
【分析】(1)要求BE=CE,题目告诉我们AB=AC,立刻想到等腰三角形三线合一,只要证明AE⊥BC即可.连接AE,直径AC所对的圆周角为直角.(2)如图6,若BD=2,BE=3,则CE= 3.连接CD,直径AC所对的圆周角为直角,在Rt△BCD中,可求得CD的长,在Rt△ACD中,设AC=x,根据勾股定理建立方程:(42)2+(x-2)2=x2,即可求出AC的长.
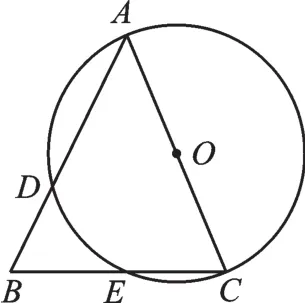
图5
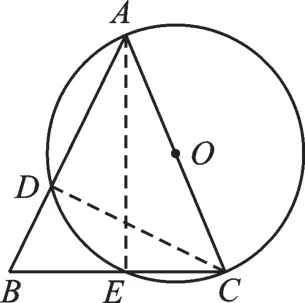
图6
【答案】AC=9.
【思考】还有其他方法求解吗?面积法能解吗?这道题我们是根据什么等量关系列方程的?
例5(2015·泰安模拟)如图7,在平面直角坐标系内,已知点A(0,6),点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
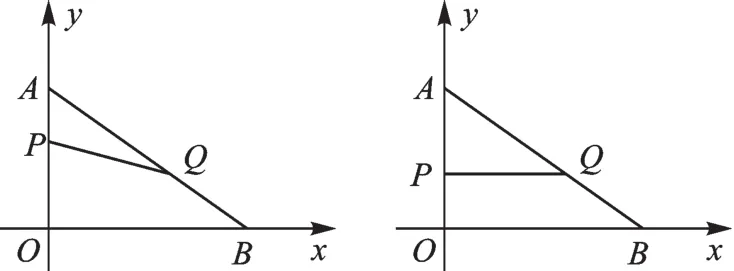
图7
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
【分析】看上去是函数问题,实际上只是几何问题给了一个函数背景,实质还是几何问题.
(1)待定系数法解决;
(2)△APQ与△AOB相似,没有明确对应关系,需要分类讨论,可以分成△APQ∽△AOB或者△APQ∽△ABO,建立方程求出t;
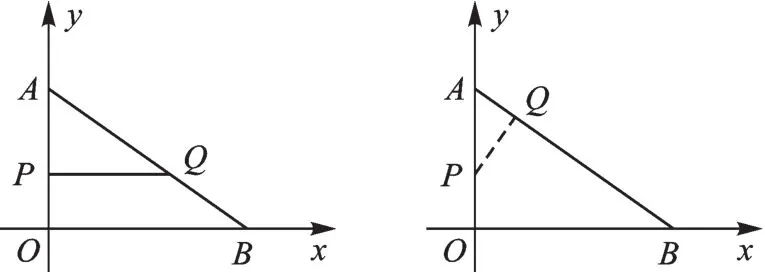
图8
【解】(1)直线AB的解析式为:y=-34x+6.
(2)如图8,∵AO=6,BO=8,∴在Rt△AOB中,根据勾股定理求得AB=10,∵运动时间为t秒,∴AP=t,AQ=10-2t.①若△APQ∽△AOB,则即:,解得(秒);②若△APQ∽△ABO,则AP=AQ,ABAO即:,解得(秒).
△AOB相似.
(3)如图9,过点Q作QE⊥AO于点E.
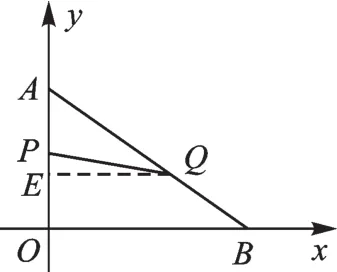
图9
∴在Rt△AEQ中,
∵S△APQ=24,5
解得t=2(秒)或t=3(秒).
在用方程解决几何问题中,我们要注意:1.先把已知条件标到图中,设未知数,用含未知数的代数式表示其余角或线段;2.利用图形的性质或定理,找到图中蕴含的等量关系,列出方程,解决问题;3.我们平时要有应用方程解决问题的意识,让方程成为我们解决几何问题的好帮手.
小试身手
1.如图10,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=______.
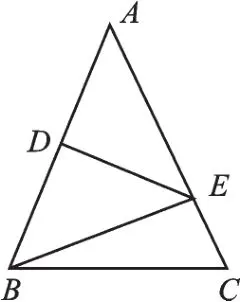
图10
2.如图11,在△ABC中,∠A=90°,AB=6,AC=8.将△ABC沿DE折叠,使点C落在AB边上的C′处,并且C′D∥AC,则CD的长是多少?
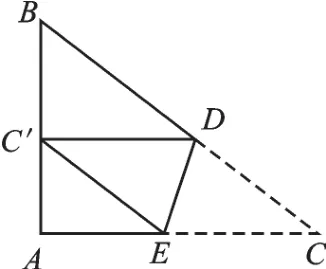
图11
3.如图12,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.(1)求证:AD平分∠BAC;(2)若BE=2,BD=4,求⊙O的半径.
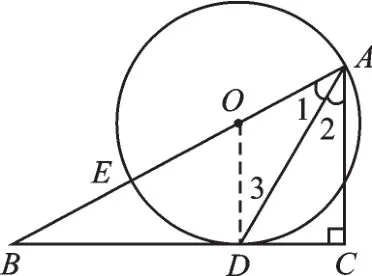
图12
(作者单位:江苏省常州市金坛区白塔中学)

扫二维码关注“初中生世界”公众号,回复“2017年6月数学”获取答案。
