利用人工模拟降雨法提高测钎法精确度

2017-06-15李纯乾李凤鸣柳金库丁宏宇丛子健赵旭珍

中国水土保持 2017年5期

关键词：土壤侵蚀坡面水土保持

李纯乾，李凤鸣，柳金库，李娜，丁宏宇，丛子健，李菲，赵旭珍

(辽宁省水土保持研究所辽宁省土壤侵蚀与水土保持重点实验室，辽宁朝阳 122000)

利用人工模拟降雨法提高测钎法精确度

李纯乾，李凤鸣，柳金库，李娜，丁宏宇，丛子健，李菲，赵旭珍

(辽宁省水土保持研究所辽宁省土壤侵蚀与水土保持重点实验室，辽宁朝阳 122000)

人工模拟降雨；测钎法；土壤侵蚀量；水土流失监测

在一定的降雨条件下，采用人工模拟降雨法与测钎法计算土壤侵蚀量并进行对比，分析两者相关性，对测钎法进行校准，以提高该方法的精确度。在雨强40 mm/h、降雨历时30 min、坡度8°、地表覆盖度0、初始土壤容重1.23 g/cm3、土壤含水量14.79%的试验条件下，测钎法计算的土壤侵蚀量结果小于人工模拟降雨法计算的结果，两者相差19%～30%。相关分析结果表明，测钎法结果与人工模拟降雨法结果之间呈极显著的正相关(R=0.981，P<0.05)。通过建立回归模型方程y=1.431x-27.237，可对同类条件下运用测钎法的计算结果进行校正，使之更加接近真实的土壤侵蚀量。未来，进一步研究在不同条件下两者之间的关系，将为利用测钎法进行野外堆土坡面水土流失监测提供更加准确的数据支持和决策指导。

野外坡面水土流失传统的监测手段是设置简易水土流失观测场，采用测钎法对坡面上的土壤侵蚀量进行观测。与水土保持监测新技术相比，测钎法的优点是操作简单，投入小，适合野外定点定位观测，不需要监测人员长期看管，不会发生设备丢失等问题，缺点是受监测手段的局限，测算结果精确度偏低。因此，对测钎设备和方法进行改良，发挥其优势，提高测量精确度，成为研究人员关注的重点。李俊等[1-2]通过改变测钎的布设方法和读数来提高结果的精确度；毕华兴等[3]提出测钎法的最低土壤侵蚀模数背景阈值，给出了测钎法的适用范围；廖章志等[4-5]研发出新的坡面监测设备。但对测钎法测量值与真实土壤侵蚀量之间关系的研究还未见报道。考虑到在实验室内采用人工模拟降雨试验收集泥沙样本进行烘干称重计算土壤侵蚀量，其结果接近真实土壤侵蚀量，具有较高的准确性，设计将人工模拟降雨法测量值与测钎法测量值进行比较，希望从中发现两者之间的关系并建立回归模型，以此对测钎法测量结果进行校正，提高测钎法的测量精确度。

1 试验材料与方法

1.1 试验区概况

试验区位于辽宁省朝阳市朝阳县波罗赤镇波罗赤村附近，属于大凌河流域，地貌区划属于燕山—辽西中低山地[6]，大凌河自南而北贯穿全区，形成中部低、两翼高的宽谷低山丘陵。土壤类型有褐土性土、淋溶褐土和褐土[7]。属温带大陆性季风气候区，多年平均气温8.9 ℃，多年平均降水量480 mm，多年平均蒸发量2 057.1 mm，多年平均风速2.8 m/s，多年平均大风天数8 d，多年平均最大冻土深135 cm。

1.2 试验设计

本试验是在辽宁省水土保持研究所试验基地的人工模拟降雨大厅进行的。人工模拟降雨设备采用中国科学院/水利部水土保持研究所与西安清远测控技术有限公司研制生产的QYJY-503固定式人工模拟降雨装置。观测小区为可调节坡度土槽。土槽中装土与土槽平行，表面进行粗糙处理，坡面尺寸1 m×2 m，在坡面上铅垂插入15根钢钎，每根钢钎之间距离30 cm，由上至下一共5排，每排3根，钢钎居中布设，距土槽上边30 cm，距土槽两边各20 cm。测钎编号顺序为从上到下、从左到右。考虑到坡面土体可能出现淤积现象，若钢钎顶部与坡面平齐，则土壤就会覆盖钢钎帽，无法进行正确的测量和读数，因此布设的每根测钎均露出地表5 cm。

试验条件设定为模拟降雨雨强40 mm/h、降雨历时30 min，观测小区坡度8°、地表覆盖度0、初始土壤容重1.23 g/cm3、土壤含水量14.79%。从地表产流开始计时，每隔3 min用500 mL广口瓶取少量径流一次，同时采用大容量桶收集并记录3 min内的径流量。在人工模拟降雨试验降雨前后分别对每根钢钎出露地表的长度进行测量和记录。为了保证试验的准确度，在相同条件下进行了5次试验。

1.3 数据分析方法

用精度到毫米的钢尺进行测钎长度测量。用量筒量取广口瓶收集的水量，用滤纸和漏斗过滤、采集广口瓶内的泥沙样，用烘箱烘干12 h后用电子天平称量。用SPSS软件进行数据相关性分析和线性回归分析，用Origin软件绘图。

人工模拟降雨法土壤侵蚀量是根据采集的泥沙质量来推算的，计算公式为

(1)

式中：Wh为人工模拟降雨法计算的土壤侵蚀量，g；wi为每个时间段末(每3 min)瞬时土壤侵蚀量，g；Vi为每个时间段(3 min)径流量，mL；vi为每个时间段末(每3 min)瞬时径流量，mL。

测钎法土壤侵蚀量计算参考《水土保持监测技术规程》(SL 277—2002)，通过降雨前后钢钎出露地表的差值计算总的土壤侵蚀量[8]。计算公式为

Wc=1 000ZSρ

(2)

式中：Wc为测钎法计算的土壤侵蚀量，g；Z为侵蚀厚度，mm；S为观测小区坡面面积，m2；ρ为土壤容重，g/cm3。

2 结果分析与讨论

2.1 测钎法与人工模拟降雨法计算结果比较

表1为分别通过公式(1)和(2)计算出的人工模拟降雨法和测钎法的土壤侵蚀量及比较情况。

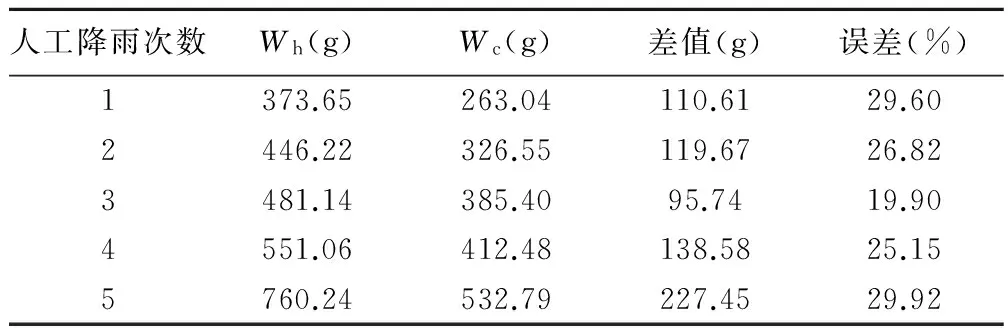
表1 用两种方法计算的土壤侵蚀量结果比较

从表1可以看出，试验条件下，测钎法计算的土壤侵蚀量与人工模拟降雨法计算的土壤侵蚀量数据有一定的误差(19%～30%)，测钎法计算结果要小于人工模拟降雨法计算结果。分析其原因，测钎法在土壤侵蚀量计算过程中仅仅考虑了坡面因地表径流引起的面蚀产生的土壤侵蚀量，因为观测方法粗糙，未考虑坡面地表径流引发的沟蚀产生的土壤侵蚀量。因此，两者相差的数值为沟蚀产生的土壤侵蚀量(临时堆土在堆放初期不能很快沉降稳定，因此本试验过程中暂不考虑土体沉降误差)。从图1可以看出在5次降雨过程中，由于降雨前期土壤含水量没能恢复到最初的数值，每次人工模拟降雨试验过程中土壤很容易达到饱和，地表径流量加大，因此每次测定的土壤侵蚀量结果均不相同，即土壤前期含水量越大，土壤侵蚀量越大。这与王辉等[9-10]研究前期土壤含水量10%～25%时土壤侵蚀量呈递增趋势的结论相符，也说明本次试验数据是可靠的。

图1 人工模拟降雨法累积土壤侵蚀量随降雨时间变化情况

2.2 相关性分析与回归模型建立

通过测钎法与人工模拟降雨法计算的土壤侵蚀量对比结果见图2。可以看出，虽然两种方法测得的土壤侵蚀量有一定的误差，但变化趋势是一致的。采用SPSS软件对测钎法计算的土壤侵蚀量与人工模拟降雨法计算的土壤侵蚀量之间的相关性进行分析，结果表明两者之间呈极显著的正相关(R=0.981，P<0.05)。通过SPSS软件进行回归分析，F=76.873>0.003，R2=0.962，建立回归方程为

y=1.431x-27.237

(3)

式中：y为人工模拟降雨法计算的土壤侵蚀量，g；x为测钎法计算的土壤侵蚀量，g。

图2 测钎法与人工模拟降雨法计算的土壤侵蚀量对比

2.3 讨论

(1)本次研究是在模拟降雨雨强40 mm/h、降雨历时30 min，观测小区坡度8°、地表覆盖度0、初始土壤容重1.23 g/cm3、初始含水率14.79%的试验条件下进行的。不同的雨强、坡度、降雨历时和地表覆盖度等会对土壤的抗冲性、入渗率产生不同的影响，其地表产流量及土壤侵蚀量结果也会不同。其他条件下测钎法与人工模拟降雨法计算的土壤侵蚀量结果之间是否也有着类似的相关性，有待于进一步试验验证。

(2)测钎法与人工模拟降雨法都是测定降雨产生土壤侵蚀量的常用方法，二者之间的差异主要是前者未考虑坡面沟蚀，因此对这两种方法之间的相关性分析实质上就是坡面面蚀和沟蚀之间的相关性分析。廖章志[11]采用测钎法对贵州省面蚀、沟蚀的土壤侵蚀量进行了研究，结果显示两者比例为1.00∶1.91，说明面蚀与沟蚀之间具有相关性。何元庆等[12]在研究堆弃土边坡土壤侵蚀量时发现，测钎法监测结果比3D激光扫描法结果小13.26%，可见测钎法测量的面蚀结果可靠性还是较高的，还能通过研究面蚀和沟蚀之间的规律性提高测钎法的精确度。

3 结论

(1)在模拟降雨雨强40 mm/h、降雨历时30 min，观测小区坡度8°、地表覆盖度0、初始土壤容重1.23 g/cm3、初始含水率14.79%的试验条件下，测钎法计算的土壤侵蚀量结果与人工模拟降雨法计算结果之间有一定的误差，范围在19%～30%，整体上测钎法计算结果小于人工模拟降雨法计算结果。误差产生的原因是测钎法未考虑到沟蚀产生的土壤侵蚀量。

(2)相关分析结果表明测钎法与人工模拟降雨法测量的土壤侵蚀量之间呈极显著的正相关关系(R=0.981，P<0.05)。两种方法测得的土壤侵蚀量有一定的误差，但变化趋势是一致的。

(3)在野外水土流失监测过程中，对与本试验相同的地表状况进行测钎法观测时，可以通过应用回归模型方程y=1.431x-27.237，对土壤侵蚀量结果进行校正，使得观测结果更加接近真实的土壤侵蚀量。

(4)进一步研究在其他条件下测钎法测算结果与真实结果之间的关系，将为野外堆土坡面水土流失监测提供更加全面准确的数据支持和决策指导，对于区域水土保持措施布设具有指导意义。

[1] 李俊,李海林,李健.关于水土保持监测中测钎应用的思考[J].水土保持应用技术,2009(1):21-22.

[2] 兰景涛,岳增璧,张保定,等.测钎法在水土保持监测应用中存在的问题及解决方案的探讨[J].西北水电,2016(1):10-13.

[3] 毕华兴,张建军.适用于测钎法的土壤侵蚀最低模数阈值探讨[J].中国水土保持科学,2016,14(5):119-122.

[4] 廖章志.测钎观测小区监测技术及应用分析[J].中国水土保持,2015(2):31-32.

[5] 杨建民,孟凡宪,丛一蓬,等.新型水土流失监测装置及其应用[J].中国水土保持科学,2016,14(4):113-120.

[6] 李炳元,潘保田,程维明,等.中国地貌区划新论[J].地理学报,2013,68(3):291-306.

[7] 董厚德.辽宁植被区划[M].沈阳:辽宁大学出版社,1987:334.

[8] 水利部水土保持司,水利部水土保持监测中心.水土保持监测技术规程:SL 277—2002[S].北京:中国水利水电出版社,2002:32-33.

[9] 王辉,王全九,邵明安.前期土壤含水量对坡面产流产沙特性影响的模拟试验[J].农业工程学报,2008,24(5):65-68.