基于扰动观测器的电液系统压力控制

熊义，魏建华，冯瑞琳，张强



基于扰动观测器的电液系统压力控制

熊义，魏建华，冯瑞琳，张强

(浙江大学流体传动及机电系统国家重点实验室，浙江杭州，310027)

针对采用流量阀作为控制元件的电液系统，设计一种基于扰动观测器的非线性鲁棒压力控制器。在该系统中，压力控制性能受到负载流量的不利影响。研究中负载流量被分成时变的未知负载流量与可以建模的泄漏流量2个部分：前者是干扰压力控制的主要因素，为此在建立系统动力学模型的基础上设计非线性扰动观测器以估计未知负载流量；应对后者的方法则是首先建立其解析模型，然后在控制器中对其进行模型补偿。基于上述两点并考虑系统动力学的非线性特性，采用滑模控制技术综合系统压力的非线性鲁棒控制器。实验结果表明：所设计控制器在存在负载流量干扰的情况下实现精确且迅速的压力跟踪控制，表现出良好的性能鲁棒性。

扰动观测器；压力控制；滑模控制；电液系统

在液压系统中，压力的无级调节一般采用比例溢流阀实现，然而比例溢流阀存在的滞环以及节流干 扰[1]等不利因素致使其压力自动化控制精度不高。闭环方法的引入有效地改进了压力控制精度，该方法通常可以分为2种形式：一种是将压力闭环控制器集成于比例溢流阀中[2]；另一种则是对整个压力回路进行闭环控制[3−4]。虽然闭环控制有效地提高了压力控制的精度，其响应速度仍受到比例阀动态性能的制约。基于高速开关阀[5−7]或基于压力伺服阀[8−10]的压力控制是通过控制流量的方式从而实现压力调节。其中，高速开关阀仅适用于流量较小的情况，往往存在压力脉动；压力伺服阀可以实现压力的高频动态控制，然而它是一种比较特殊的产品，在一般的电液系统中并不通用。在另一些采用流量阀的液压压力伺服控制应用中，如液压施力系统[11−12]以及密闭容腔[13−14]等，系统没有受到显著的负载流量干扰。本文作者考虑一种采用流量阀实现压力控制的电液系统应用场合，针对其中存在的未知、时变的负载流量干扰以及液压系统的一些非线性特性[15]，如压力/流量的映射关系，设计了一种基于扰动观测器的非线性鲁棒控制器。该控制器可以通过扰动观测器[16−18]估计未知负载流量，进而实现对干扰的控制补偿。同时，控制器采用滑模控制技术[19−20]以应对电液系统中的非线性、模型偏差和估计误差。最终，所设计控制器的压力控制性能在实验中得以验证。

1 问题描述

本文所研究的对象可简化为图1所示的模型。系统由恒压源提供高压油，通过一个高频响阀调节一个固定容积容腔中的压力c，从该容腔流出的流量分为泄漏流量p与未知负载流量l。p是可以建模的，其模型为压力c的函数。l的模型是完全未知且时变的。

图1 对象模型

受控容腔压力的动态为

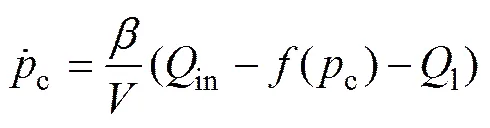
式中：c为固定容腔中的压力；in为高频响阀调节的输入流量；为液压油体积弹性模量；为容腔容积；(c)为p的模型，是一个关于c的光滑函数；l为集中的未知干扰流量，包括模型误差。

in是通过高频响阀的流量，其映射表达式为

式中：q为高频响阀的综合流量系数；s为压力源压力；为高频响阀的控制电信号。阀的动态被省略是基于其动态频宽远高于压力响应动态频宽的假设。

系统控制目标为即使存在负载流量p与l的干扰，仍然能够综合有界的控制信号去动态调节高频响阀的流量输入，从而使容腔压力c能够以一定的精度跟随期望压力指令d。接下来将设计能够实现这一目的的控制器。

2 控制器设计

假设1：未知扰动流量l的时间导数是有界的，满足条件

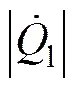
对于系统(1)设计非线性扰动观测器为

式中：o为观测器的增益；为干扰流量l的估计；为扰动观测器的内动态。通过式(4)可推出的时间导数满足

(5)

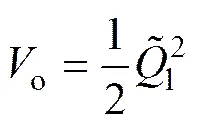
o的时间导数为

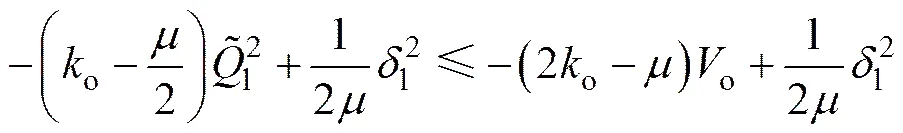
且得

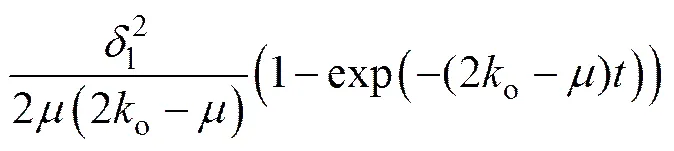
式中：为一个任意的正数。从式(8)可以推出，只要满足k＞/2，扰动观测器(4)的估计误差就会指数收敛到原点附近一个半径为的圆形区域内。因此，估计误差由，o与决定，并且

(9)

接下来设计镇定系统的鲁棒控制器。首先令pc−d表示受控压力的跟踪误差。定义误差的滑模切换面为

(11)

其时间导数为

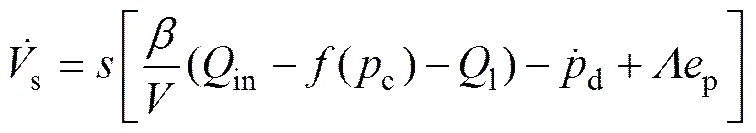
设计输入流量in的控制函数为

(13)

式中：a补偿了系统的建模泄漏流量、估计干扰流量和期望压力动态，为模型补偿控制项；s为鲁棒控制项，包括名义镇定反馈控制、压力误差反馈控制和非连续的鲁棒控制；s为正的反馈增益。也是1个正数，满足

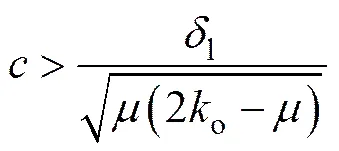
图2所示为控制器的原理框图。

图2 控制器原理框图

Fig. 2 Principle diagram of proposed controller

定理：对于系统(1)，如果假设1成立，并且采用式(13)综合流量输入，那么系统能够实现对期望压力的精确跟踪，且瞬态控制过程具有鲁棒性。

证明 将式(13)代入式(12)可以得到

(16)

因为是一致连续的，所以当→∞，→0。收敛过程满足。证毕。

以上设计的控制输入为流量输入，用式(2)将其映射为阀的控制信号

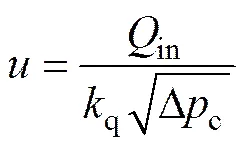
利用式(17)计算时需要先知道的符号，这显然是不合理的，然而根据式(2)可知的符号与in的相同，所以，是可以通过in的符号计算的。

3 实验研究

3.1 实验系统

图3所示为实验系统的原理图。系统控制阀是REXROTH公司生产的高频响阀，型号为4WRREH6VB40L，其额定流量为单边压差3.5 MPa下40 L/min，正弦频响不低于80 Hz。模拟的未知负载流量是通过负载流量阀调节实现的，该阀与控制阀完全一样。受控容腔为不充气的蓄能器空腔。泵源压力s设为10 MPa。压力传感器是IFM公司产品，量程为10 MPa，其线性度误差小于±0.25%，滞环在±0.2%之内。控制程序在上位机Simulink Real-Time环境下编写，由下位机实时系统运算执行，上、下位机通过以太网通讯。控制器采样频率设为1 kHz。控制信号及传感器信号分别通过NI公司PCI 6259数据采集卡生成和采集，其数/模与模/数转换器分辨率均为16位。图4所示为控制块的实物照片。

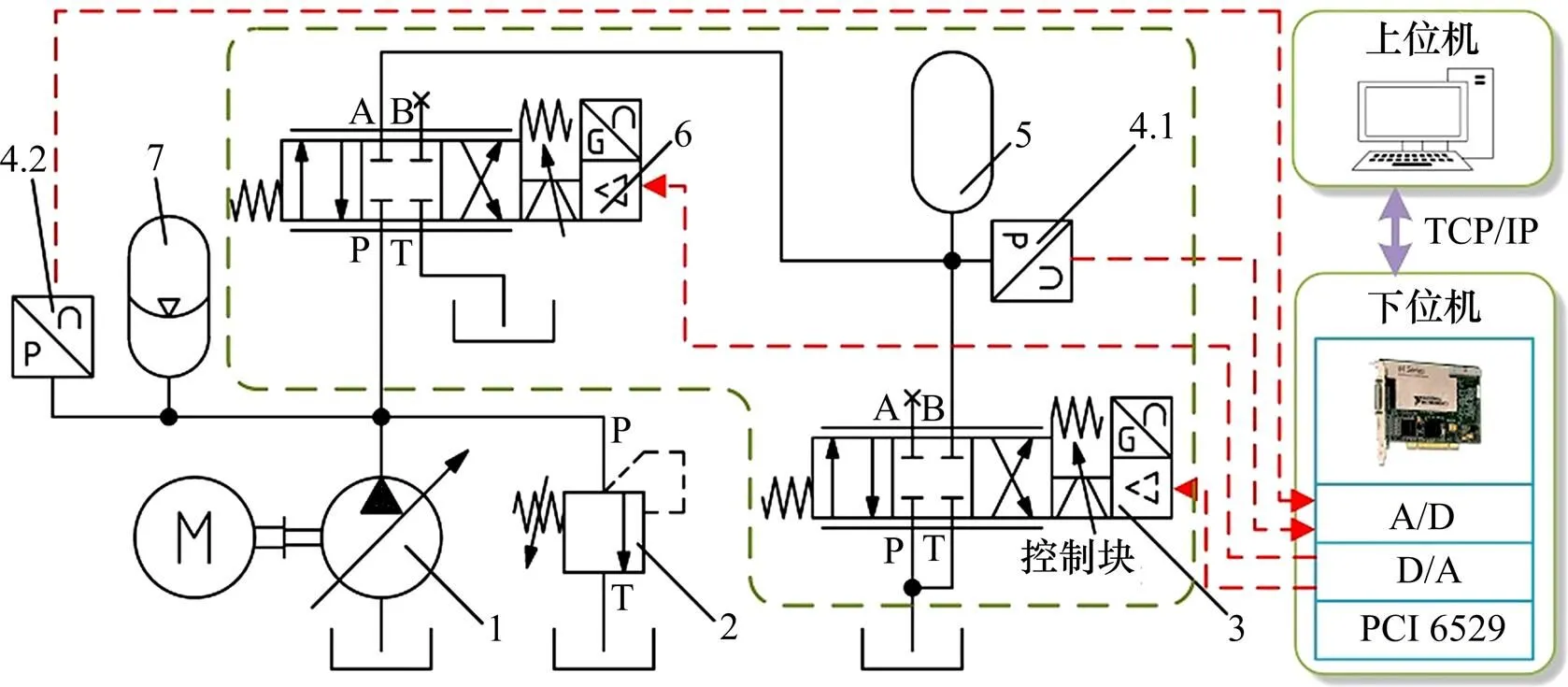
1—液压泵；2—溢流阀；3—负载流量阀；4—压力传感器；5—受控容腔；6—控制阀；7—蓄能器。

图4控制块照片

3.2 模型识别及参数设定

首先对泄漏流量p=(c)进行建模：如图3所示，将控制块上负载流量阀的B口堵死，将控制阀开口打开50%开度，调节变量泵与溢流阀将受控容腔的压力逐级提升，压力信号c通过压力传感器采集，从泵流入控制块的流量p则用流量计测得，该流量计的量程范围为0.02~4 L/min。图5所示为流量p相对于压力c的实测数据与拟合曲线。

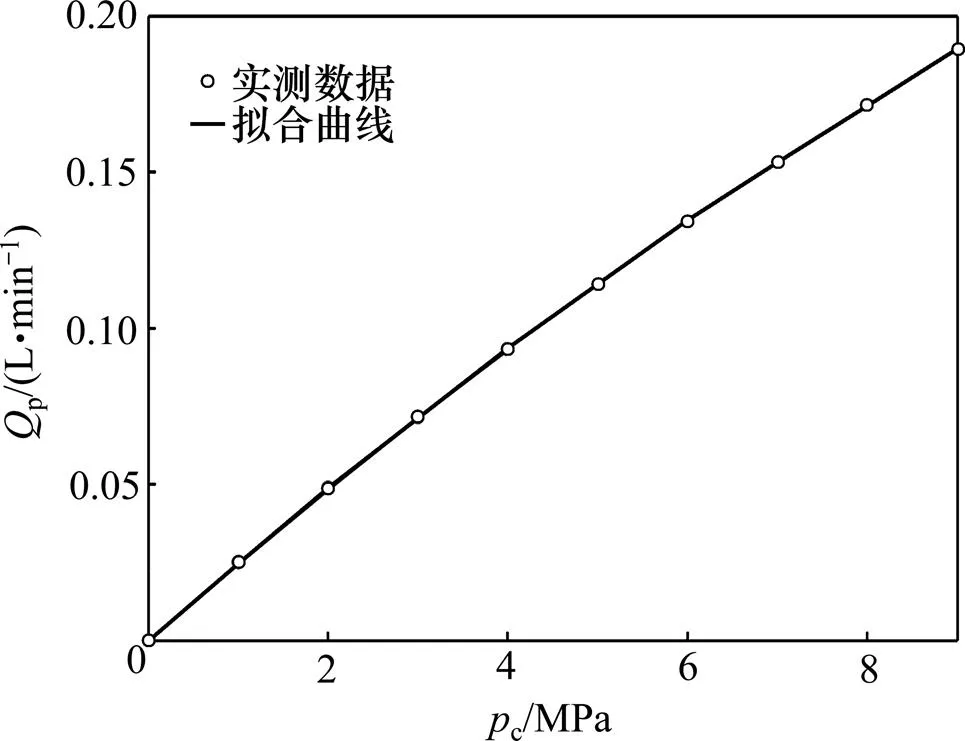
图5 泄漏流量Qp相对于压力pc的曲线

通过对图5中数据的拟合确定泄漏流量的模型为

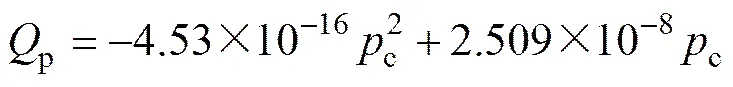
控制器中需要用到的受控对象模型参数见表1。其中受控容腔容积的确定：如图3所示，将负载流量阀替换为二通球阀并将其截止，将控制阀的A口置于高位灌入液压油直至容腔全部被填充，然后将球阀打开，用量杯从控制块回油口收集灌入的油液。此外，参数与q通过查阅手册、产品样本以及理论估算得到。实验中使用的控制器控制参数经过调试确定，其数值见表2。

表1 系统模型参数

表2 控制器参数

实验对控制器进行了简化：非连续控制项−sign()被省略。实际上在应用中并不需要定理中全局收敛的结论，只要保证一定的稳定工作范围就已足够。

3.3 实验结果分析

实验中首先测试了系统对于快速指令的响应性能，将阶跃信号经过滤波后作为期望压力指令信号输入控制器，滤波器的传递函数为。图6所示为负载流量阀0，15%和30%开度下，系统对1~9 MPa期望指令的响应曲线以及误差曲线。

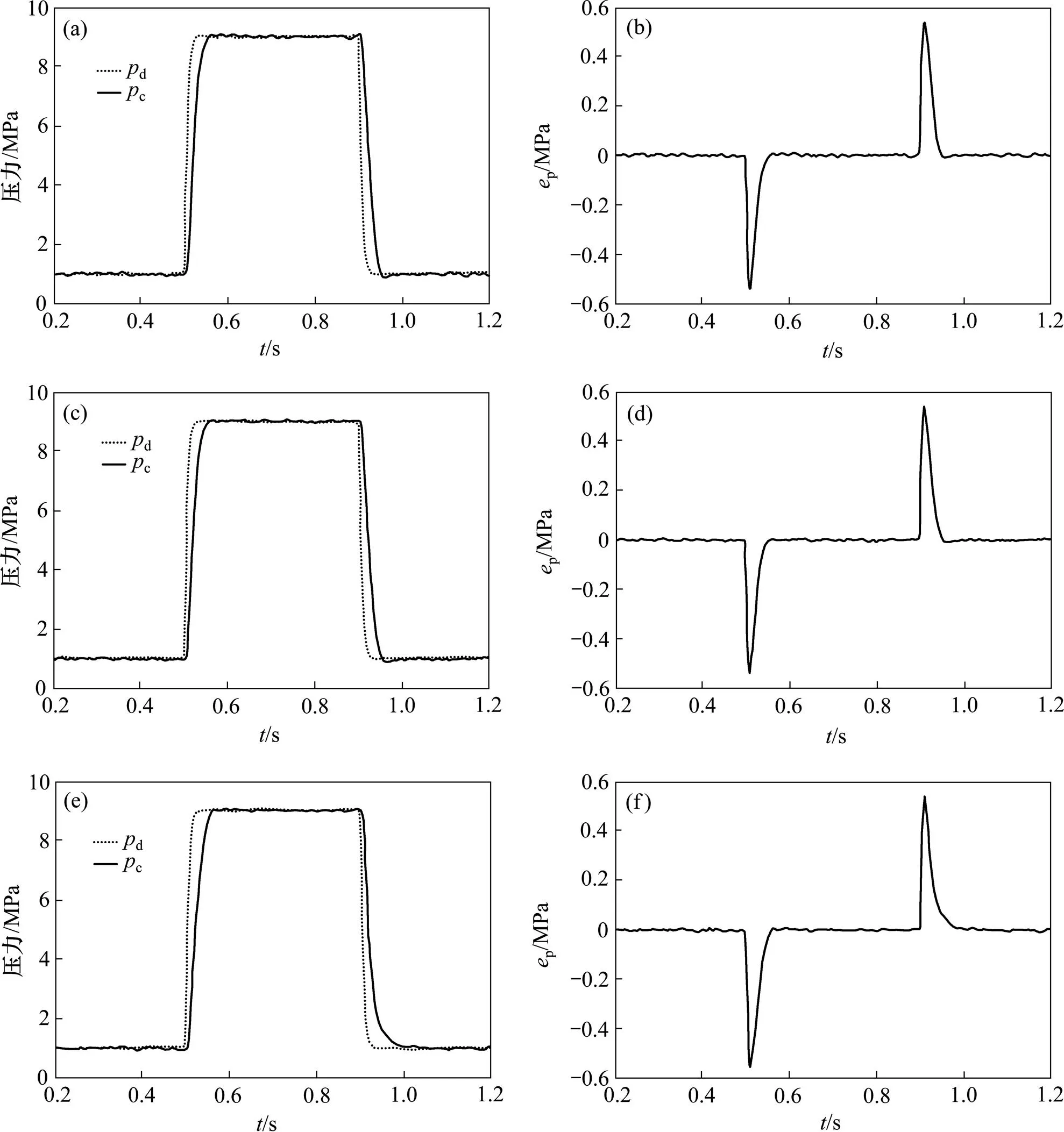
负载流量阀开度/%：(a), (b) 0；(c), (d) 15；(e), (f) 30

由图6可见：实验中指令信号从0到100%需要约40 ms。在负载流量阀0%开度时，系统响应的上 升/下降时间不超过55 ms，超调量小于1.7%；在负载流量阀15%开度时，上升/下降时间不超过57 ms，超调量小于1.25%；而在负载流量阀30%开度时，上升/下降时间不超过60 ms，无明显超调(有超调时，上升/下降时间取响应曲线瞬态过程相对于指令0↔100%的时间，无超调时取0↔95%的时间)。此外，上述3个对比试验中，压力的稳态误差均在±0.15 MPa以内，而且图6中的瞬态误差的峰值非常接近，均小于0.56 MPa。综上，在不同的未知负载流量干扰下，控制器的性能没有明显的变化，表现出性能鲁棒性。图7所示为上述3个实验中未知负载流量的估计值与理论值曲线。未知负载流量的理论值用下式计算：

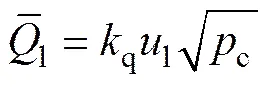
式中：q为负载流量阀的综合流量系数(与控制阀相同)；l为负载流量阀的控制电信号。

由图7可见：当干扰流量为稳定值时，扰动观测器能准确地给出估计，然而在瞬态过程中，估计值与理论值存在较大差异。这一现象符合式(9)的结论，当观测器设计参数o和确定时，估计误差就取决于l。在瞬态过程中，干扰流量迅速变化，于是l的取值较大，估计误差明显；而处于稳态时，l取值为0，因此，估计误差很小。此外，从式(4)可知：未知负载流量估计的动态还与c和in等有关，在瞬态过程中，这些变量剧烈变化也是导致估计误差明显的原因。

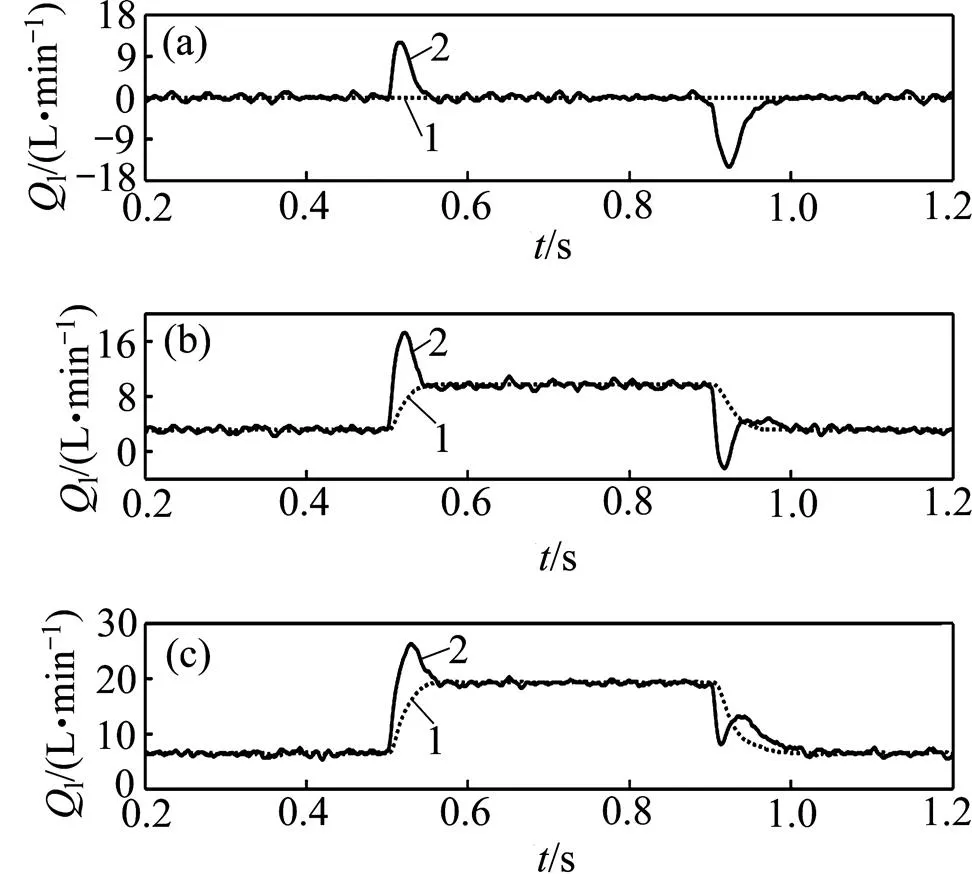
负载流量阀开度/%：(a) 0；(b) 15；(c) 30

接下来将控制指令设为5MPa的固定常值，让负载流量阀作开度5%↔25%的阶跃开合，以进一步测试控制器在扰动剧烈变化下的控制性能。该测试中的响应曲线见图8，未知负载流量估计曲线见图9。图8中流量的阶跃扰动发生在0.5 s(开)与0.9 s(合)，系统在经过不到100 ms的短暂瞬态调整过程之后便进入稳定状态，并且受控压力c的波动在0.38 MPa以内。此外，如图9所示，在该测试过程中，扰动观测器仍然保持了对未知负载流量的准确估计。

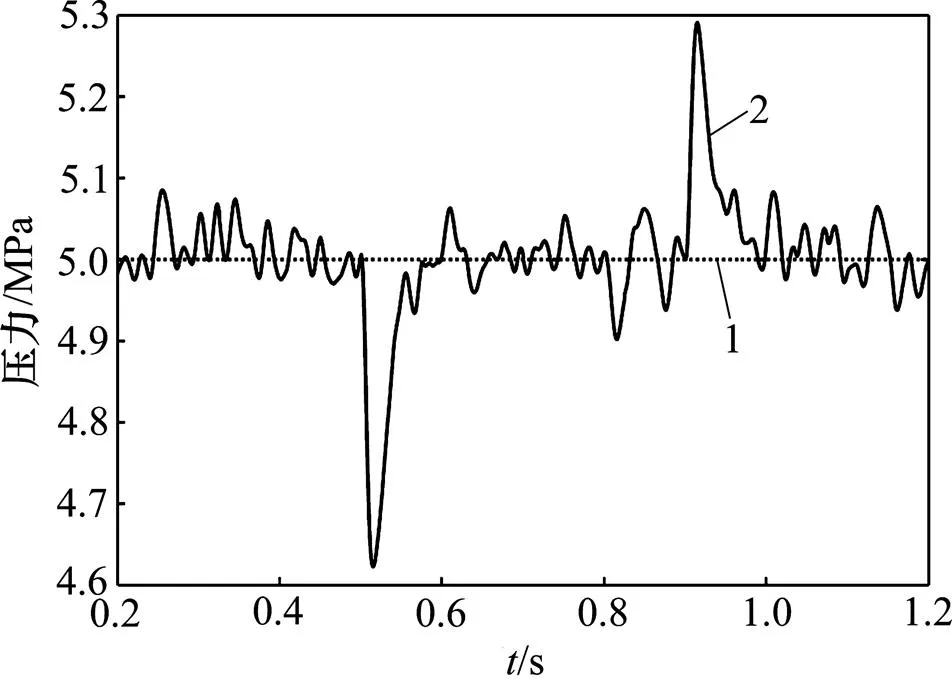
1—pc；2—pd。

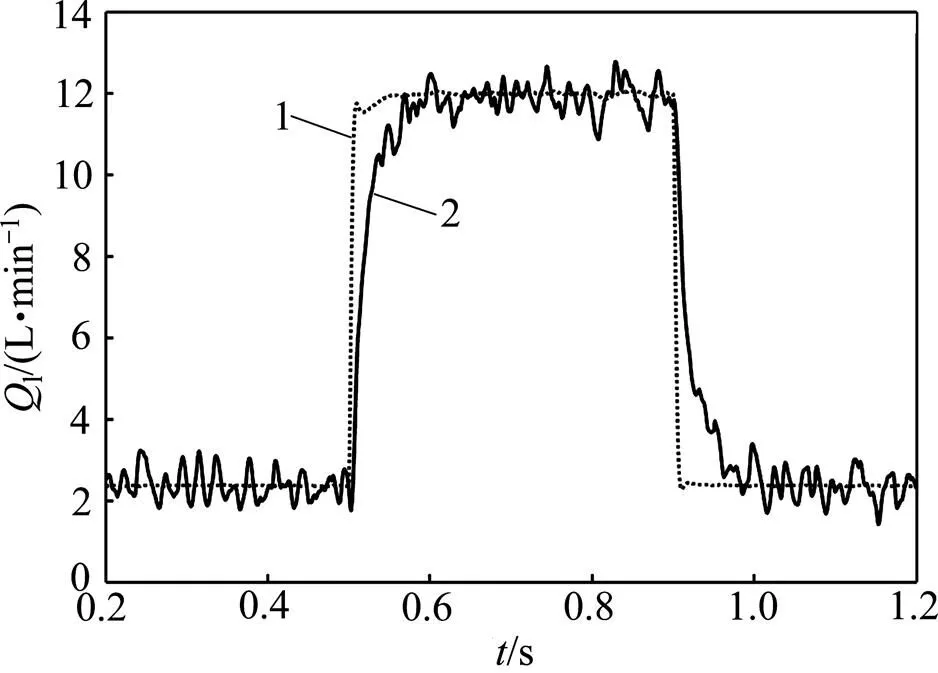
1—负载流量理论值；2—负载流量估计值。

除了以上针对快速指令以及快速扰动的测试外，还对控制系统进行了压力正弦跟踪控制实验，以验证控制器在未知负载流量连续变化情况下的性能。此时，控制指令为

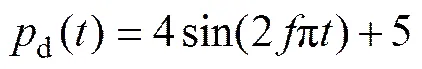
其中：为正弦指令的频率。

图10所示为负载流量阀开度为15%时，系统对指令(20)的跟踪误差，包括1，2，3 Hz共3种频率，图11所示为对应3种情况下的未知负载流量估计值与理论值曲线。由图10可见：系统跟踪1 Hz指令时的误差绝对值|p|＜0.37 MPa；2 Hz时，|p|＜0.82 MPa；3 Hz时，|p|＜1.31 MPa。此实验中随着正弦指令速度的加快，跟踪误差随之增大，不仅如此，图11中未知负载流量的估计值相对于理论值的偏差也在增加。这种性能的退化一方面是因为控制系统本身频宽的限制；另一方面，在实验中负载干扰流量边界函数l取值随着压力变化频率的增加而增大，于是，扰动观测器的估计精度有所下降，控制补偿效果也相应 衰减。

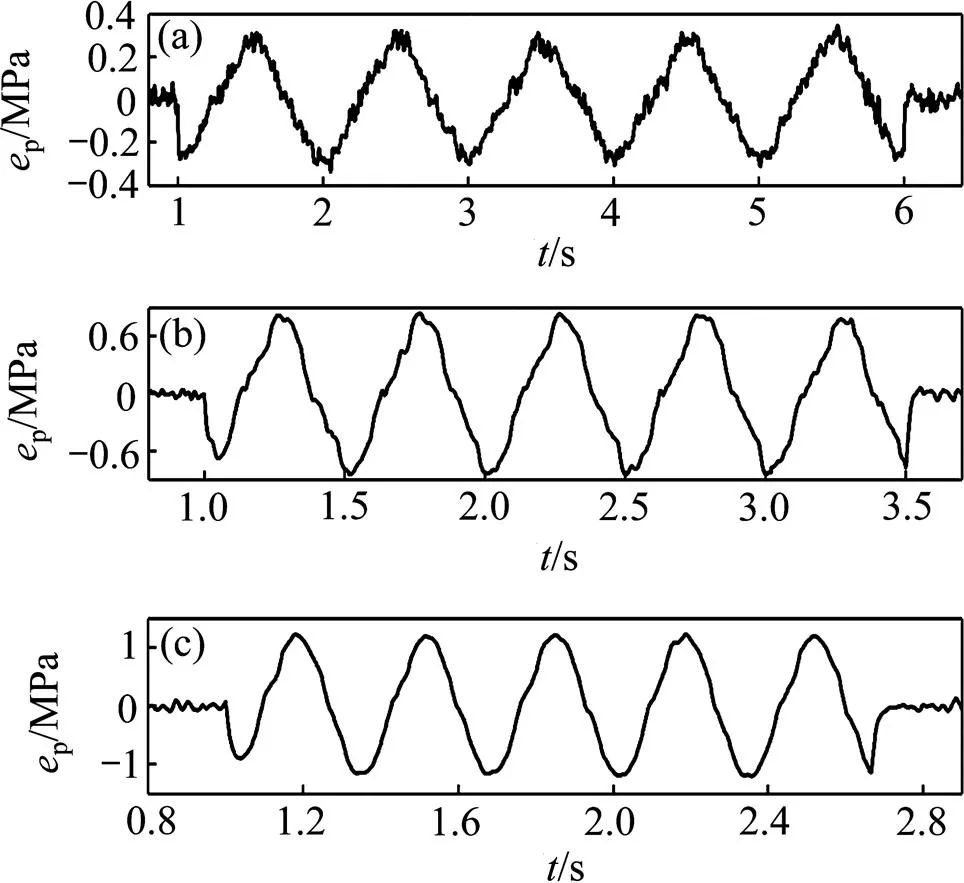
f/Hz: (a) 1; (b) 2; (c) 3

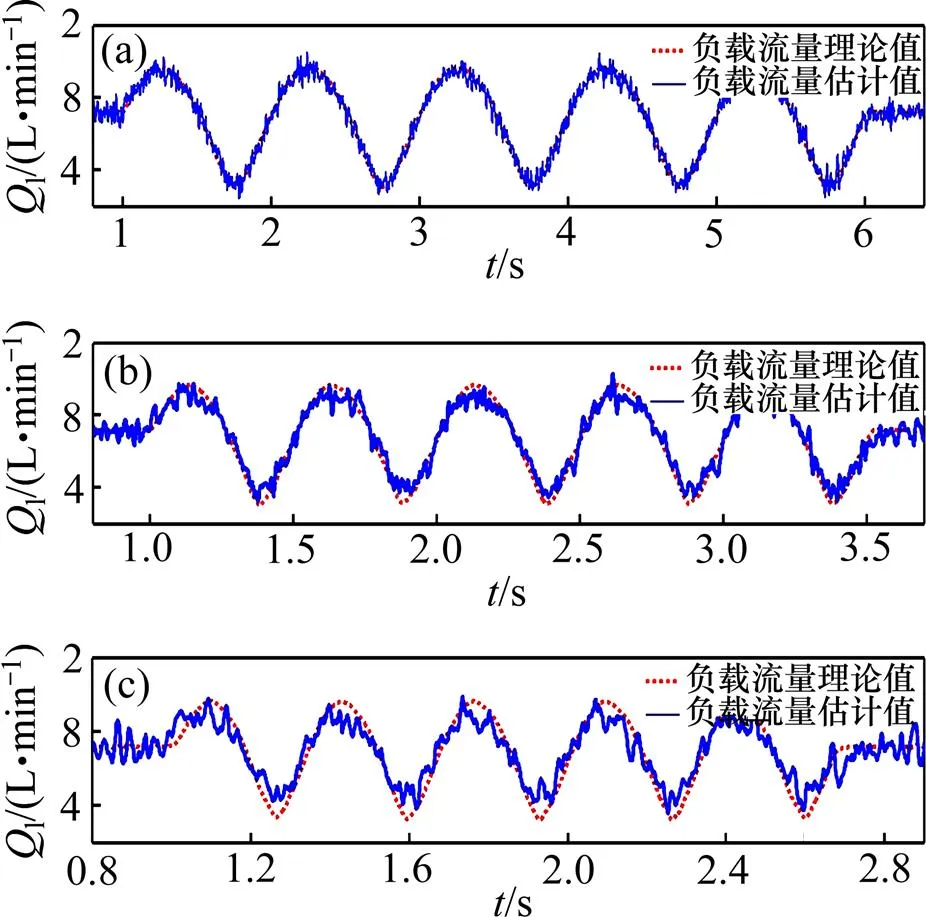
f/Hz: (a) 1; (b) 2; (c) 3

最后通过扫频实验测试了系统的频宽，其幅值及相位伯德图如图12所示。控制指令采用式(20)，负载流量阀开度为15%，此时，系统的−3 dB幅值频宽约为9 Hz，−90°相位频宽约为21 Hz。

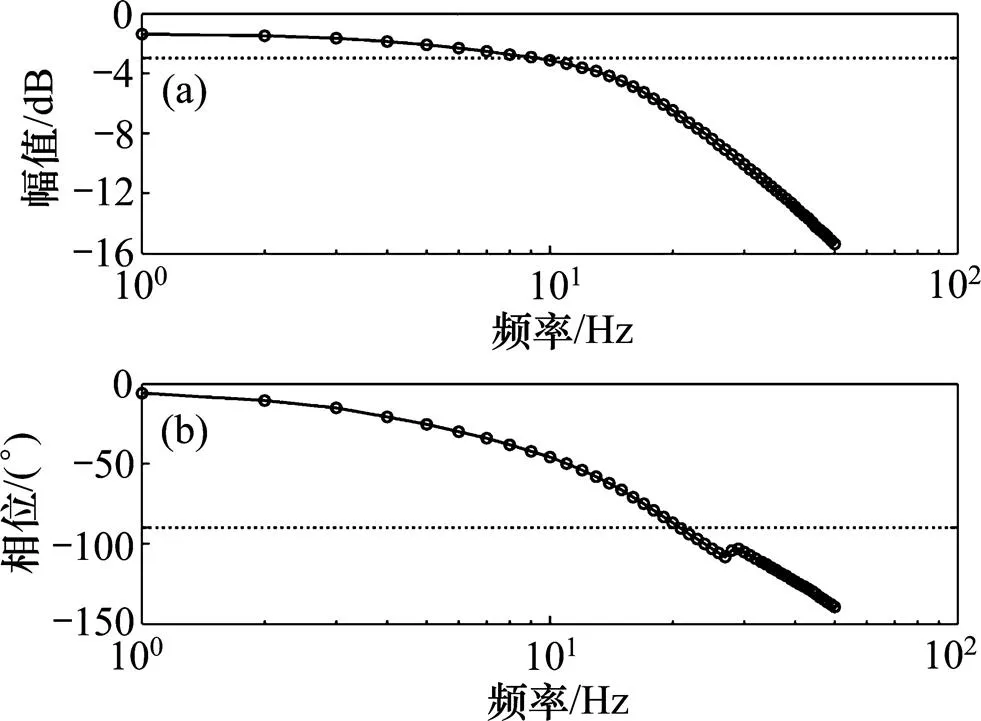
图12 控制系统伯德图

4 结论

1) 建立流量阀控制容腔压力系统的非线性压力动态模型，考虑其中可建模的泄漏流量和不可建模的未知负载干扰流量。通过实验确定泄漏流量的解析模型以及容腔容积。

2) 基于系统模型，设计可以估计未知负载干扰流量的扰动观测器，将其与滑模控制技术相结合设计系统的非线性鲁棒控制器，并理论证明了该控制器可以保证鲁棒的瞬态性能和确定的稳态精度。

3) 通过一系列针对性实验测试所设计控制器的性能。在实验中，扰动观测器可以准确地估计未知负载干扰流量，在此基础上控制器实现快速的动态响应以及精确的稳态精度，并且具有一定的抗干扰能力，表现出性能鲁棒性。综上，基于扰动观测器的非线性鲁棒控制器可以有效地解决存在未知负载干扰流量情况下流量阀控制容腔压力的问题。

[1] 吴根茂, 邱敏秀, 王庆丰, 等. 新编实用电液比例技术[M]. 杭州: 浙江大学出版社, 2006: 114−131. WU Genmao, QIU Minxiu, WANG Qingfeng, et al. Electrohydraulic proportional technique in theory and application[M]. Hangzhou: Zhejiang University Press, 2006: 114−131.

[2] 赵辉, 杨帆, 王金亮. ATOS比例溢流阀在钢管水压试验机中的应用[J]. 焊管, 2014, 37(7): 27−30. ZHAO Hui, YANG Fan, WANG Jinliang. Application of ATOS proportional relief valve for steel pipe hydrostatic tester[J]. Welded Pipe and Tube, 2014, 37(7): 27−30.

[3] 李贵闪, 翟华. 液压机液压系统比例压力控制方法探讨[J]. 机床与液压, 2011, 39(16): 67−68. LI Guishan, ZHAI Hua. Discussion on methods of proportional pressure control in hydraulic system of hydraulic press[J]. Machine Tool & Hydraulics, 2011, 39(16): 67−68.

[4] 吴军强. 基于电液比例的液压机压力闭环控制研究[D]. 成都: 西华大学机械工程学院, 2011: 17−19. WU Junqiang. Research on the pressure close-loop control of hydraulic press based on electro-hydraulic proportional technology[D]. Chengdu: Xihua University. School of Mechanical Engineering, 2011: 17−19.

[5] WANG F, GU L, CHEN Y. A hydraulic pressure-boost system based on high-speed on-off valves[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(2): 733−743.

[6] MORIWAKE Y, AKAGI T, DOHTA S, et al. Improvement of pressure control type quasi-servo valve and on/off valves using embedded controller[C]// Proceedings of 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). New York: IEEE, 2013: 882−887.

[7] LE M Q, MINH T P, MOREAU R, et al. Comparison of a PWM and a hybrid force control for a pneumatic actuator using on/off solenoid valves[C]// Proceedings of 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). New York: IEEE, 2010: 1146−1151.

[8] 何学工, 黄增, 金瑶兰, 等. 射流管式电液压力伺服阀技术研究[J]. 机床与液压, 2013, 41(10): 60−62. HE Xuegong, HUANG Zeng, JIN Yaolan, et al. Technical research on jet pipe type electrohydraulic pressure servo valve[J]. Machine Tool & Hydraulics, 2013, 41(10): 60−62.

[9] 黄英玲. 基于工控机的直驱式电液压力伺服阀数字控制的研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2008: 10−12. HUANG Yingling. Research on digital control of direct drive pressure control servo valve based on industry personal computer[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2008: 10−12.

[10] TUNAY I, RODIN E Y, BECK A A. Modeling and robust control design for aircraft brake hydraulics[J]. IEEE Transactions on Control Systems Technology, 2001, 9(2): 319−329.

[11] 杜随更, 银东东, 余少军. 线性摩擦焊机电液伺服施力系统动态特性[J]. 上海交通大学学报, 2008, 42(S1): 35−37. DU Suigeng, YIN Dongdong, YU Shaojun. Dynamic characteristics of electro-hydraulic servo load system of linear friction welding machine[J]. Journal of Shanghai Jiaotong University, 2008, 42(S1): 35−37.

[12] ZHU W H, PIEDBOEUF J C. Adaptive output force tracking control of hydraulic cylinders with applications to robot manipulators[J]. Journal of Dynamic Systems, Measurement, and Control, 2005, 127(2): 206−217.

[13] 李宝仁, 刘浩, 傅晓云. 密闭容腔压力伺服控制系统理论与实验研究[J]. 液压与气动, 2004(7): 1−3. LI Baoren, LIU Hao, FU Xiaoyun. Theoretical and experimental research on pressure servo control system of closed chamber[J]. Chinese Hydraulics & Pneumatics, 2004(7): 1−3.

[14] 李宝仁, 张庆先, 杜经民. 高精度压力伺服控制系统研究[J]. 液压气动与密封, 2000(2): 10−11. LI Baoren, ZHANG Qingxian, DU Jingmin. A high accuracy pressure servo system[J]. Hydraulics Pneumatics & Seals, 2000(2): 10−11.

[15] NOAH D M. Hydraulic control systems[M]. New Jersey: John Wiley & Sons, Inc., 2005: 60−88.

[16] CHEN Wenhua. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(4): 706−710.

[17] YANG Jun, CHEN Wenhua, LI Shihua. Non-linear disturbance observer-based robust control for systems with mismatched disturbances/uncertainties[J]. IET Control Theory and Applications, 2011, 5(18): 2053−2062.

[18] WON D, KIM W. Disturbance observer based backstepping for position control of electro-hydraulic systems[J]. International Journal of Control, Automation and Systems, 2015, 13(2): 488−493.

[19] KOMSTA J, VAN OIJEN N, ANTOSZKIEWICZ P. Integral sliding mode compensator for load pressure control of die-cushion cylinder drive[J].Control Engineering Practice, 2013, 21(5): 708−718.

[20] ZIRKOHI M M, LIN T C. Interval type-2 fuzzy-neural network indirect adaptive sliding mode control for an active suspension system[J]. Nonlinear Dynamics, 2015, 79(1): 513−526.

(编辑 陈爱华)

Disturbance observer based pressure control for electrohydraulic system

XIONG Yi, WEI Jianhua, FENG Ruilin, ZHANG Qiang

(The State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China)

Considering the electrohydraulic systems controlled by flow valves, a disturbance observer based nonlinear robust pressure controller was developed. The proposed method mainly focuses on the disturbance arising from load flow, which can be divided into two parts. One part is unknown and time-varying, named unknown load flow, which significantly affects pressure control in electrohydraulic systems. The other part can be modeled, named leakage flow. To account for the disturbance caused by unknown load flow, a nonlinear disturbance observer was designed to estimate it. The leakage flow was handled by model compensation in the controller. Based on the estimation of unknown load flow and the model of leakage flow, also taking into account nonlinear characteristics associated with the pressure dynamic at the same time, a nonlinear robust controller was synthesized via sliding mode control technology. Theoretically, the controller can achieve guaranteed robust transient performance and steady-state control accuracy. The proposed controller was tested on an experiment set. The experiment results show that using the raised controller, the system achieves fast and precise pressure tracking control, and the control performance is robust to unknown load flow.

disturbance observer; pressure control; sliding mode control; electrohydraulic system

10.11817/j.issn.1672-7207.2017.05.009

TH137

A

1672−7207(2017)05−1182−08

2016−07−06；

2016−09−29

国家自然科学基金资助项目(51075359) (Project(51075359) supported by the National Natural Science Foundation of China)

魏建华，教授，博士生导师，从事电液控制理论研究与应用研究；E-mail: jhwei@zju.edu.cn