基于侧偏特性的车辆转弯直径精确计算方法

李 辰，张军伟，杨 波，齐 鸣，付有兵

(北京航天发射技术研究所， 北京 100076)

【机械制造与检测技术】

基于侧偏特性的车辆转弯直径精确计算方法

李 辰，张军伟，杨 波，齐 鸣，付有兵

(北京航天发射技术研究所， 北京 100076)

车辆设计之初一般采用阿克曼原理进行车辆最小转弯直径的计算，由于其未考虑轮胎侧偏特性，导致计算结果误差较大。针对该问题，提出了一种考虑轮胎侧偏特性的车辆转弯直径计算方法，以某四轴越野车辆为研究对象，开展理论公式推导，根据轮胎试验数据拟合得到轮胎侧偏刚度，完成转弯直径的计算。与实车试验数据进行对比分析，结果表明：该方法计算误差小，能够准确计算车辆的转弯直径。

多轴车辆；阿克曼原理；侧偏特性；转弯直径

在转向系统的设计过程中，一般要求转向车轮的转角关系满足阿克曼原理。然而，阿克曼原理仅适用于车辆速度特别小、侧偏角为零的情况，是零速度下的静态条件[1-2]。

对于虚轴位置并不与非转向桥所在轴线重合的车辆，由于轮胎的侧偏特性，导致其转向时的实际情况与阿克曼原理的理想工况差别较大。设计人员在使用阿克曼原理进行车辆最小转弯直径的计算时，得到的计算结果与真实情况往往有较大的偏差，不能很好地指导设计[3-6]。

综上所述，急需一种兼具较高精度与可实施性的车辆转弯直径计算方法，以满足快速设计、分析的需要。

1 阿克曼原理计算

以某四轴越野车辆为研究对象，其转向方式为双前桥转向，虚轴位于三、四桥轴距之半处，如图1所示。以阿克曼原理为基础，可利用图解法或解析法进行转弯直径的计算。

图1 研究对象阿克曼原理示意图

根据阿克曼原理，利用解析几何的方法，得到其理论转弯直径的表达式为

(1)

式中L=2L1+2L2+L3

α为1桥内轮最大转角；B为轮距；K为主销中心距；L1为1、2桥轴距；L2为2、3桥轴距；L3为3、4桥轴距。

根据设计经验，这种以阿克曼原理为基础计算车辆转弯直径的方法，由于未考虑轮胎的侧偏特性，对于虚轴位置与非转向桥所在直线并不重合的车辆，计算得到的结果与实际情况偏差大。同时，得到的理论转弯直径与车速无关，与实际情况不符[7]。因此，需要一种兼具高计算精度以及简便可行的方法计算车辆的转弯直径，为设计提供帮助及依据。

2 考虑侧偏特性时车辆转弯直径的计算

针对上述问题，建立车辆转向行驶仿真模型。建立车辆坐标系xoy，坐标系原点与汽车质心重合。在分析计算中做出如下假设：忽略悬架的作用，车辆只作平行于地面的平面运动；车身不发生侧翻现象，轮胎的侧偏刚度值表达式处于线性范围；驱动力不大，不考虑地面切向力对轮胎侧偏特性的影响；没有空气动力的作用；忽略左、右车轮轮胎由于载荷的变化引起轮胎特性的变化以及轮胎回正力矩的作用。

这样，实际车辆便可以简化成由有侧向弹性的轮胎支承于地面、具有侧向以及横摆运动的二自由度车辆模型，如图2所示。

车辆各转向轮之间由杆系机械相连，其相互之间的关系唯一确定。当1桥左侧车轮的转角为δ1L时，相应的1桥右侧车轮转角为δ1R，2桥左侧车轮转角为δ2L，2桥右侧车轮转角为δ2R。

图2 二自由度车辆模型

当车辆进行转向时，由于轮胎存在侧偏现象，在侧偏力Fij(i=1,2,3,4; j=L,R)的作用下，各车轮的侧偏角为aij。侧偏角为矢量，其正负根据计算结果确定。其中，侧偏力Fij与侧偏角aij的关系为

(2)

式中k为侧偏刚度。

此时，各车轮中心接地点处的实际运动速度与x轴的夹角θij为

(3)

将1桥左侧车轮侧偏角a1L以及1桥右侧车轮侧偏角a1R设为未知数，根据式(3)可以得到1桥左侧车轮以及1桥右侧车轮的实际运动速度方向。做两条直线OB1L与OB1R，使其分别通过1桥左侧车轮以及1桥右侧车轮的中心接地点并垂直于两车轮的实际运动速度方向。联立直线OB1L与直线OB1R，得到的交点即为车辆转向时的旋转运动中心点O。

得到车辆转向时旋转运动中心点O的坐标后，即可通过计算直线OBij的斜率kObij，求得2、3、4桥各车轮的侧偏角aij

(4)

可知，各车轮侧偏角均为1桥车轮侧偏角以及1桥左侧车轮转角的函数，即aij= f(a1L,a1R,δ1L) (i=2,3,4; j=L,R)。

当车辆在一固定车轮转角下进行等速圆周运动行驶时，其运动微分方程分别为：

车辆沿y轴的横向运动微分方程

(5)

车辆绕z轴的横摆运动微分方程

(6)

式中：m为整车总质量；r为横摆角速度；u为纵向速度，即车辆的前进速度。

1桥左侧车轮中心接地点处的实际运动速度与x轴的夹角θ1L还可以由质心侧偏角β = v/u表示为

(7)

联立式(3)与式(7)，得到1桥左侧车轮的侧偏角a1L

(8)

同理，得到1桥右侧车轮的侧偏角a1R为

(9)

联立式(8)与式(9)，求解得到车辆横摆角速度r的表达式为

(10)

联立式(2)、式(4)、式(5)、式(6)、式(10)，即可求解得到所有未知量，进而得到转弯直径D的表达式

(11)

将上述思路重新进行梳理，绘制流程框图如图3所示。

图3 流程框图

3 设计参数的确定

3.1 轮胎台架试验

对本文所研究车辆的轮胎进行特性测试试验。试验中，对轮胎施加一个垂直载荷，将轮胎充气至目标气压后，变换不同侧偏角，启动滑台带动轮胎匀速运动，记录各侧偏角所对应的侧向力与回正力矩数值，完成纯侧偏试验，试验装置如图4所示。轮胎实际使用中的冷态气压为790 kPa，考虑到车辆行驶过程中轮胎气压虽有所升高，但由于试验速度较低，试验过程中轮胎气压基本不变。为了使试验测试状况与实际使用状态更为接近，试验中参照美国通用汽车公司的全球标准GMW15204以及文献[8]，轮胎试验气压比使用气压高20 kPa，试验时轮胎气压设定为810 kPa。

图4 轮胎台架试验

将轮胎在高附着系数试验路面(水泥路面)上进行试验，依次施加不同的垂直载荷，得到的侧向力与侧偏角的试验关系曲线如图5所示。

图5 轮胎侧向力与侧偏角的试验关系曲线 (高附着系数路面)

对线性区域侧偏角范围内的侧向力与侧偏角数据进行线性拟合，计算得到试验轮胎的侧偏刚度。并将轮胎侧偏刚度(单位：N/deg)与垂直载荷(单位：kN)间的数据完成拟合，拟合得到一条5次方函数(各项系数取4位有效数字)：

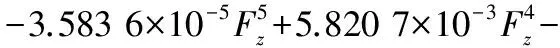
(12)

轮胎侧偏刚度试验值与拟合值如表1所示。

3.2 转向轮实际转角关系

在进行转向系统设计时，以阿克曼原理得到的理论转角为目标转角，进行转向杆系关键点的优化设计。以1桥内侧车轮转角为自变量，得到优化后的其他转向轮转角关系曲线如图6所示。

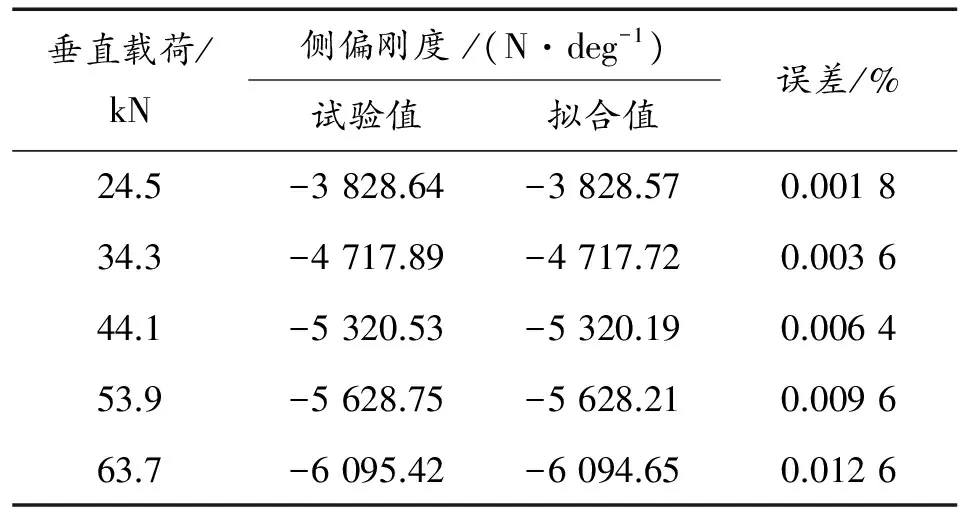
表1 轮胎侧偏度实验值与拟合值对比

图6 实际转向轮转角关系曲线

以1桥内侧车轮转角31°为例，此时其他各车轮转角角度如表2所示。从表2可以看出，转向系统关键点设计较为理想，实际转角与理论转角误差较小。

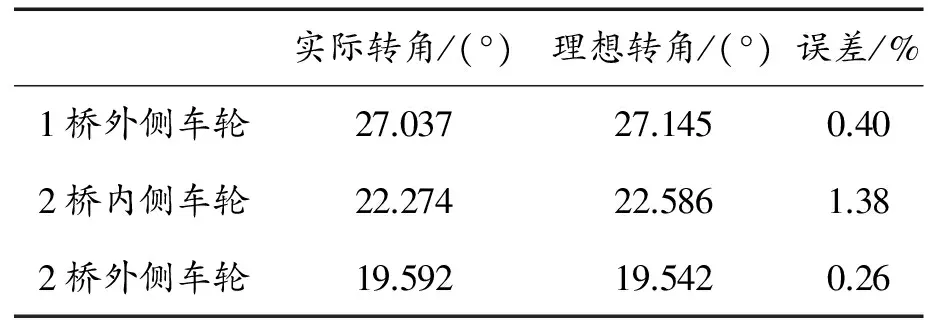
表2 车轮转角角度

4 仿真计算结果及实车测试

根据上述实验与拟合计算结果，汇总仿真所需的相关车辆参数如表3所示。

以图3中所示的计算方法为基准，代入表3中的参数进行仿真计算，计算结果如表4所示。

将表4的数据绘制成曲线，如图7、图8所示。

从仿真计算结果可知，随着车速的增加，被研究车辆具有如下特性：

1) 转弯直径逐渐减小，即底盘具有过多转向角度；

2) 虚轴至1桥的距离逐渐减小，即虚轴位置不断前移；当以较低车速行驶时，虚轴的计算位置位于设计位置之后，当车速增加到一定值后，虚轴的计算位置位于设计位置之前；

3) 在车速1～20 km/h范围内，横摆角速度增益与车速之间处于近似线性关系；

4) 3桥车轮侧偏角恒为正值，其绝对值逐渐减小，其余车轮侧偏角恒为负值，绝对值逐渐增大；

5) 由于3、4桥为非转向桥，虚轴位置并不与其重合，故3、4桥车轮侧偏角较大，可能会使轮胎具有较明显的磨损现象。

表3 仿真参数

对被研究车辆进行实车转弯直径测试，测试中将车速控制在5 km/h左右，得到测试结果如表5所示。

将阿克曼原理方法计算结果、考虑侧偏特性方法仿真结果(车速5 km/h)、实车测试结果进行整理，如表6所示。

表4 仿真计算结果

图7 车辆转弯直径仿真曲线

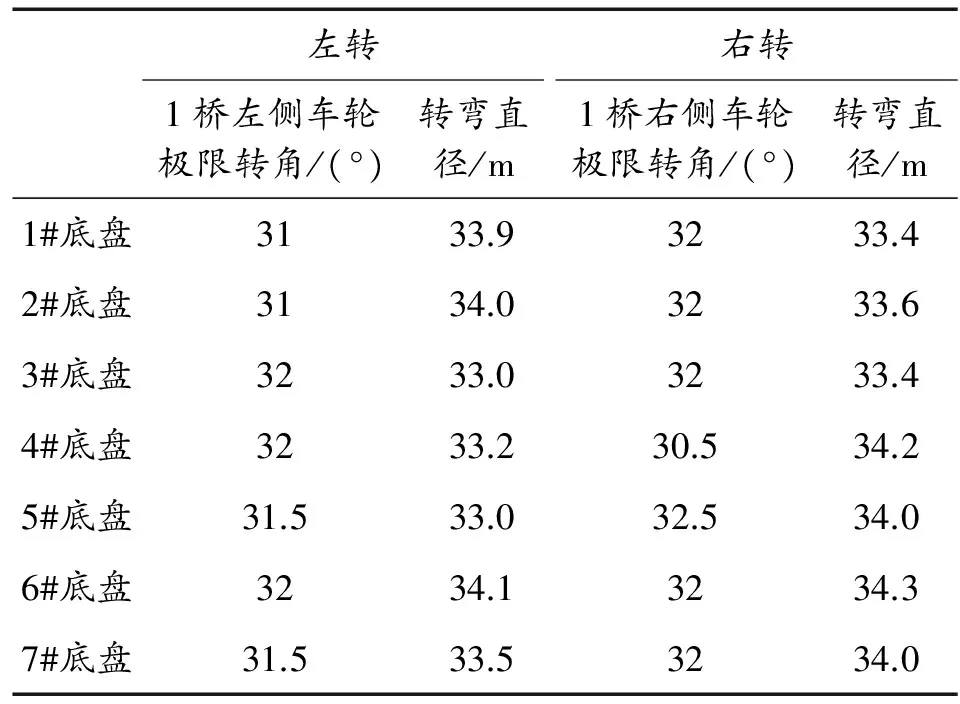
左转1桥左侧车轮极限转角/(°)转弯直径/m右转1桥右侧车轮极限转角/(°)转弯直径/m1#底盘3133．93233．42#底盘3134．03233．63#底盘3233．03233．44#底盘3233．230．534．25#底盘31．533．032．534．06#底盘3234．13234．37#底盘31．533．53234．0

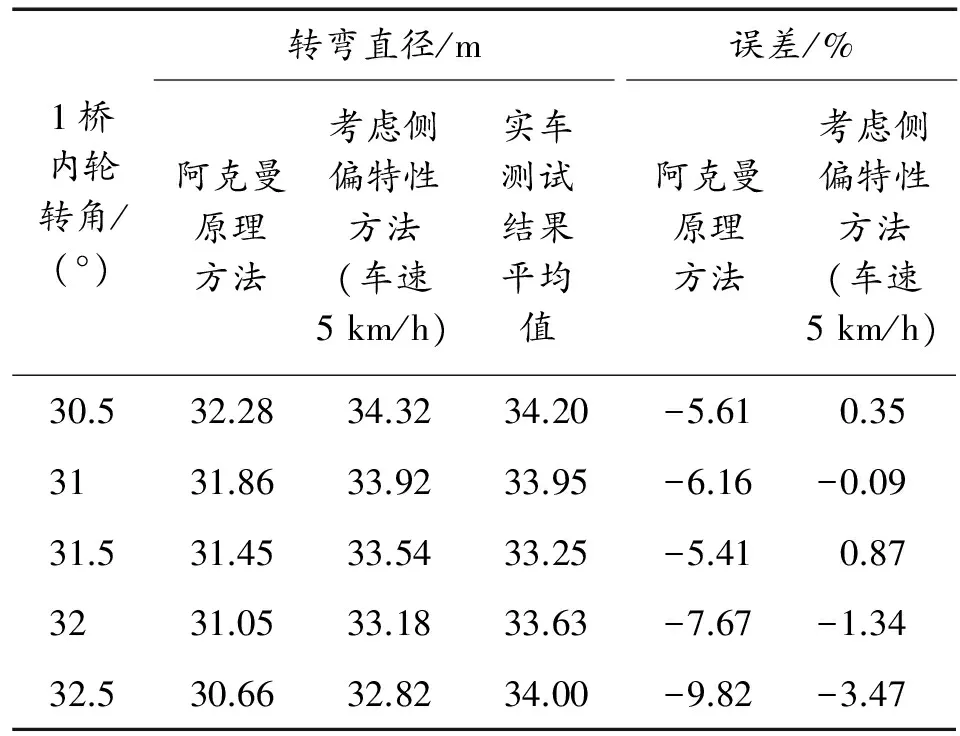
表6 转弯直径对比值

由以上数据可以看出，传统阿克曼原理计算方法得到的转弯直径值误差较大(误差均大于5%)；而文中所介绍的考虑轮胎侧偏特性计算方法能够将计算精度大大提高(误差均小于3.5%)，得到的结果与仿真计算值基本一致。证明本研究所述方法的正确性，具有较高的精度与准确性，简单、实用、具有可执行性，能够为设计提供重要的参考依据。

仿真计算结果与试验得到的车辆转弯直径有一定的误差。经过分析，误差主要来源于以下几方面：

1) 假设条件

本文中的仿真计算是以数个假设条件为前提的，忽略了一些相关条件，例如驱动力、轮胎回正力矩等因素的影响。

2) 轮胎特性的不一致性

由于轮胎特性具有不一致性，针对一个轮胎所进行的台架试验，得到的实验结果并不能够完全符合所有轮胎。

3) 杆系调整误差

在车辆总装完成后需要进行转向杆系的调整，由于车架、转向系统、悬架系统等零部件的加工误差，以及转向桥前束值的存在等因素，导致转向杆系的最终调整值总与设计值存在偏差。

4) 转向杆系的变形以及间隙等

在进行计算时，将转向拉杆以及转向臂均认为是刚体，而不考虑其存在的变形；同时，对于拉杆与臂之间的间隙亦忽略不计。然而，在实际情况中，变形与间隙均是实际存在的。

5) 最小转弯直径试验误差

在对车辆进行最小转弯直径试验时，也存在多种因素将导致产生误差，例如：车速的控制、车轮转角的控制、路面情况、测量误差，等。

5 结论

1) 利用阿克曼原理进行车辆转弯直径计算的传统方法，其结果误差较大，不能为设计提供精确值，本研究提出了一种考虑轮胎侧偏特性的计算方法，其得到的结果具有较高的精度与准确性。

2) 以二自由度车辆模型作为研究对象，将侧偏特性考虑其中，建立了一种计算车辆在前轮角阶跃输入下的稳态响应计算方法；并对所用轮胎进行了台架试验，得到了轮胎特性的测试值，并将其侧偏刚度值的表达式线性化，作为仿真计算的输入。

3) 以某四轴重型越野车辆为研究对象，通过仿真在前轮角阶跃输入下的稳态响应，得到某些重要信息，如具有过多转向角度等。

4) 通过仿真得到车辆转弯直径的计算值，并进行实际车辆的转弯直径测试，两者结果基本一致，证明其有较高的计算精度。

5) 本研究采用的方法可行性较高，得到的结果较为准确，能够为设计提供精确、重要的参考依据。

[1] 余志生.汽车理论[M]. 5版.北京：机械工业出版社，2009.

[2] 刘昭度.汽车学[M].北京：高等教育出版社，2012.

[3] 王超.五轴重型车辆转向杆系结构分析[D].长春：吉林大学，2011.

[4] 王科星，胡国强.特种车辆后轴转向方案研究[J].北京汽车，2011(4)：22-25.

[5] 张维远.多轴转向汽车基于Matlab/Simulink的转向特性研究[D].长春：吉林大学，2011.

[6] 彭莫，周良正，岳惊涛，等.多轴汽车[M].北京：机械工业出版社，2014.

[7] BORIS N B，SERGEI D P.Heavy-Duty Wheeled Vehicles:Design,Theory,Calculations[M].[S.l.]:[s.n.],2014.

[8] 卢荡，郭孔辉.轮胎侧偏力学特性的胎压影响分析[J].吉林大学学报(工学版)，2011，41(4)：915-920.

[9] 杨舒涵，王春燕，赵万忠．主动前轮转向车辆操纵稳定性的仿真分析[ J]． 重庆理工大学学报(自然科学)，2015(1)：16-22．

(责任编辑 唐定国)

Research on Accurate Computational Method of Turning Diameter of Vehicle Based on Cornering Properties

LI Chen, ZHANG Jun-wei, YANG Bo, QI Ming, FU You-bing

(China Academy of Launch Technology (CALT), Beijing 100076, China)

The Ackerman principle is used to design the minimum turning diameter in the first beginning of vehicle development. However, the cornering properties of tire are not considered that results in large range of computation error. A kind of computation method of turning diameter which considers the cornering properties is developed to study a four-axle vehicle. The cornering stiffness is fit by test data so as to compute the turning diameter. The comparison of simulation result and test data proves that the new computation method obtains mild error and high accuracy.

multi-axle vehicle; Ackerman principle; cornering properties; turning diameter

2016-12-15；

2017-01-26 基金项目：国家自然科学基金资助项目(51605020) 作者简介：李辰(1988—)，男，硕士研究生，工程师，主要从事车辆底盘理论与设计研究。

张军伟(1986—)，男，博士研究生，工程师，主要从事多轴重型车辆互连式油气悬架系统特性、重型车辆悬架系统设计、多轴车辆系统动力学仿真、动力总成振动优化研究。

10.11809/scbgxb2017.05.030

format:LI Chen, ZHANG Jun-wei, YANG Bo, et al.Research on Accurate Computational Method of Turning Diameter of Vehicle Based on Cornering Properties[J].Journal of Ordnance Equipment Engineering,2017(5):130-135.

U461

A

2096-2304(2017)05-0130-06

本文引用格式：李辰，张军伟，杨波，等.基于侧偏特性的车辆转弯直径精确计算方法[J].兵器装备工程学报，2017(5):130-135.