头部和尾舵布局对弹箭俯仰气动特性影响

倪 曼，陈少松，张鲸超

(南京理工大学， 南京 210094)

【装备理论与装备技术】

头部和尾舵布局对弹箭俯仰气动特性影响

倪 曼，陈少松，张鲸超

(南京理工大学， 南京 210094)

采用数值模拟的方法并经过风洞实验验证分析了超音速下无翼式布局火箭弹模型俯仰气动特性随头部形状和尾舵面积的变化规律，得出在头部长细比固定不变的条件下选用单锥型弹头较双锥形弹头有更好的稳定性；选用面积大的尾舵具有更好的法向过载和稳定性；为无翼式布局弹箭气动设计提供了依据。

无翼式布局弹箭；头部形状；尾舵面积；气动特性

无翼式布局火箭弹由弹身和一组布置在弹身尾部的尾翼组成[1]。由于取消了主翼面，使得弹身的质量以及气动阻力大为降低，没有主翼的干扰使舵面效率大为提高。因此，无翼式布局近年来广泛应用于制导火箭弹中。无翼式布局制导火箭弹的速度域宽，要保证全程静稳定飞行难度大，主要有两方面的原因：一、随着速度向超音速增加，压心向前移动[2]，其前移量超过由发动机燃烧带来的质心前移量，使全弹静稳定性下降；二、尾舵面积受到铰链力矩的限制[3]，不能大幅增加，难以单增加尾舵面积提高稳定性。

从外形布局看，无翼式布局制导火箭弹头部外形是影响静稳定的重要因素，头部法向力提供非稳定的力矩，减小头部非稳定力矩是提高全弹静稳定的重要措施。因此，头部的形状、尾舵的面积是影响无翼式布局火箭弹气动特性的重要因素，通过改变各个部件的形状和尺寸大小可以改善全弹的气动性能。倪金付[4]采用风洞实验，分析了无翼式布局火箭弹分别采用尖拱形和双锥形头部的气动特性，得出了采用尖拱形头部的火箭弹模型具有更好的升阻力特性和法向特性、双锥形头部在俯仰操纵方面具有更好的静稳定性的结论，但对头部形状不同影响气动特性变化的原因没有分析和解释。刘德广[5]从工程应用的角度出发，得出了测算超音速下无翼式布局弹箭舵面法向力系数的方法，其方法和思路对于弹翼气动力的测算有一定的参考价值。本文首先通过数值计算(CFD)得到无翼式布局火箭弹俯仰气动特性随头部形状和尾舵面积的变化规律，然后用风洞实验结果证明数值计算的可行性，最后分析各部件对全弹气动力的贡献，结合流场分析解释。

1 数值计算

分别对超音速下三种不同头部和三种不同尾部的无翼式布局火箭弹模型进行数值计算，得到各气动参数随攻角的变化规律。

1.1 计算模型及计算区域

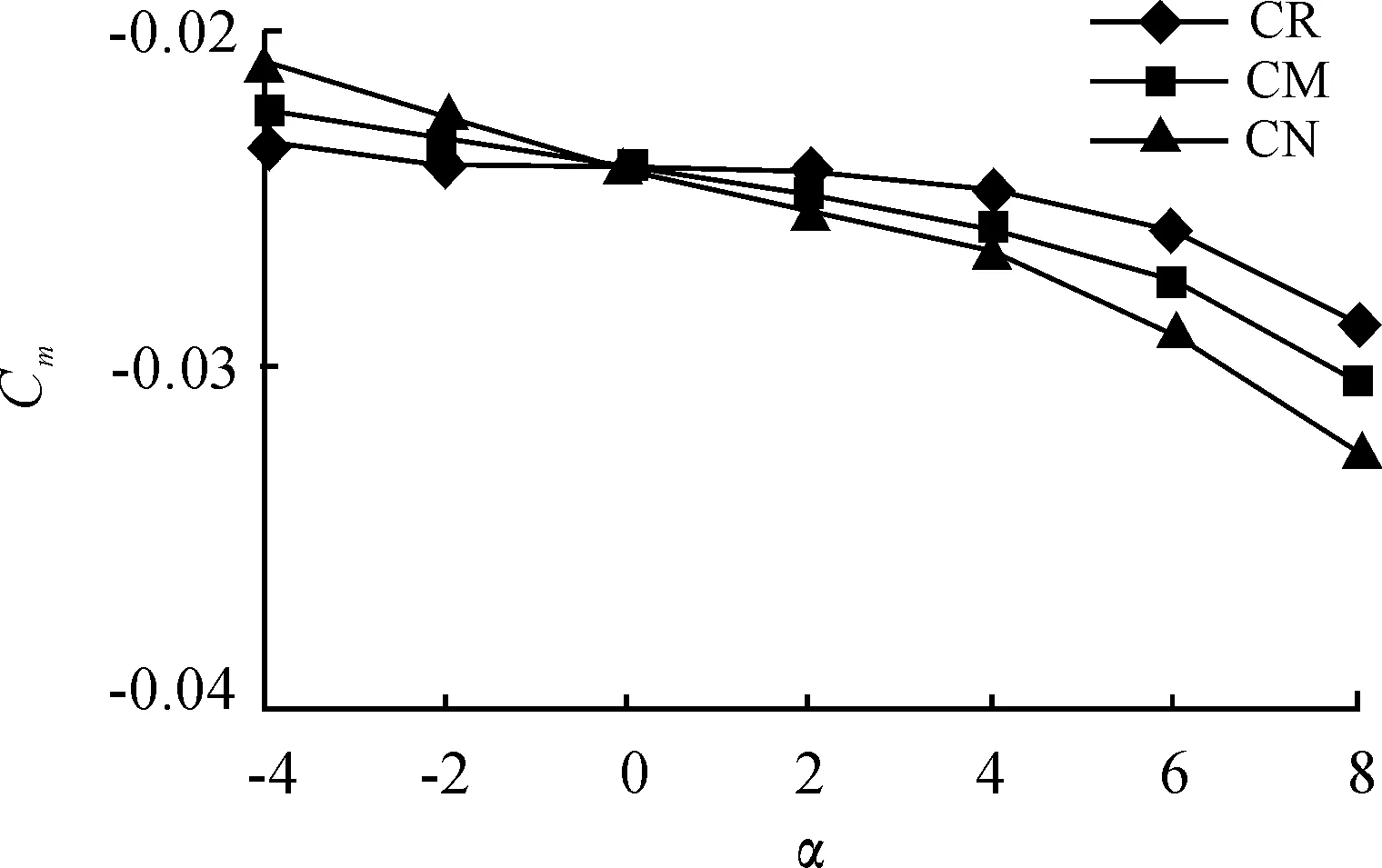
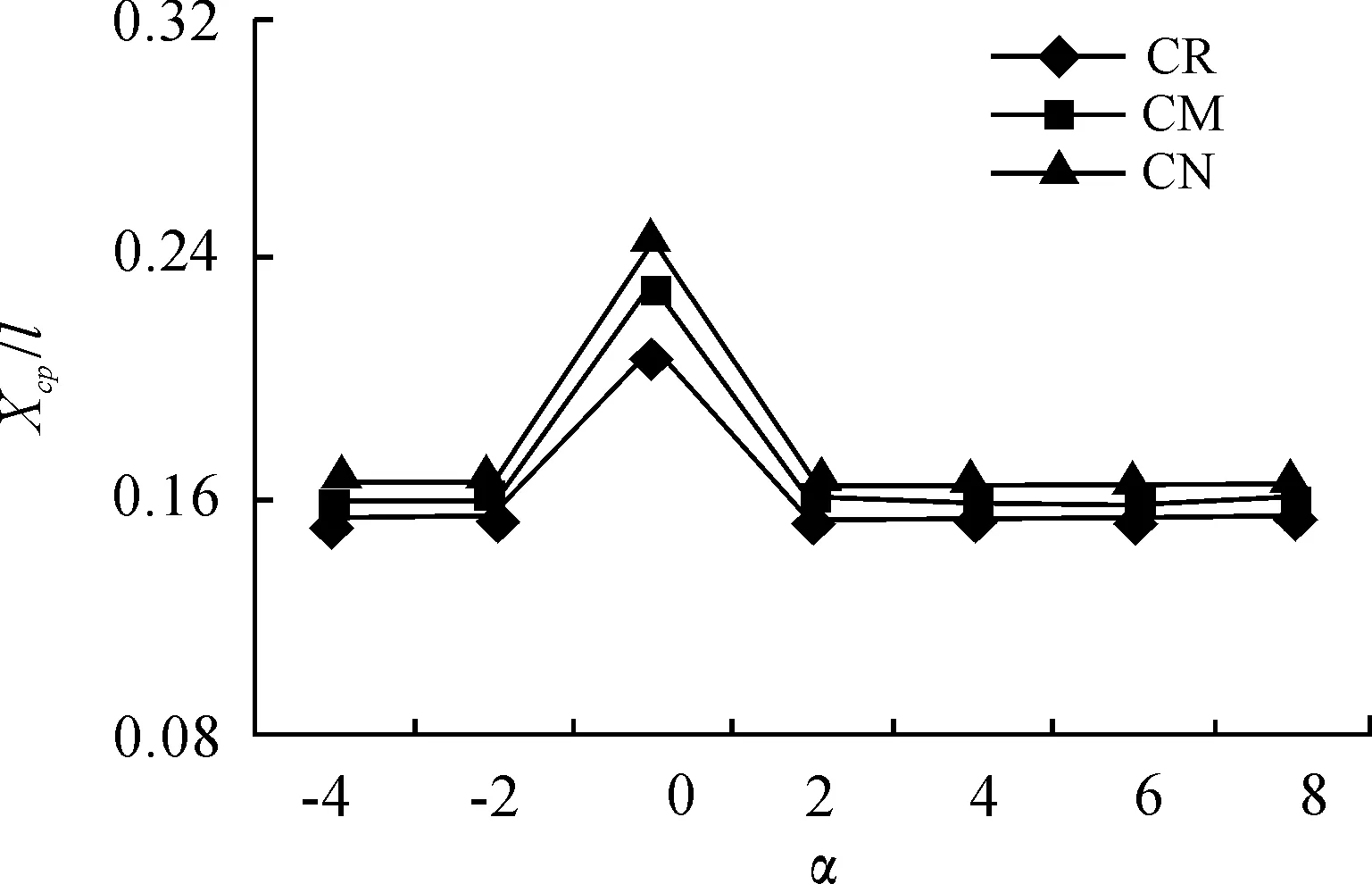
本文运用Solidworks建立了三种外形不同但长细比相同的头部模型，代号分别为 C、D、P，头部锥角大小依次是 C 型>D 型>P 型，其中C、D型为双锥形，P为单锥形；建立了三种不同面积的尾舵模型，代号分别为R、M、N，三个尾舵展长保持相同,面积大小依次是R型

图1 不同头部形状火箭弹计算模型

图2 不同尾舵面积火箭弹计算模型

1.2 计算方法

数值模拟采用三维Navier-Stokes方程[6]为基本方程，将Spalart-Allmaras模型[7]作为本次数值模拟的湍流模型，边界条件采用无反射条件的压力远场边界条件区域。计算区域为包含模型的圆柱型区域，由于模型在超音速范围内，弹体轴向前场取1.4倍弹径，弹体径向取35.7倍弹径，运用ICEM进行结构化网格划分，网格数量在320万～340万。几何模型的网格如图3所示。

图3 CM模型网格示意图

1.3 计算条件

本文数值模拟的来流攻角α分别为-4°、-2°、0°、2°、4°、6°、8°；来流马赫数Ma分别为3.0和4.0；来流静压P∞分别为71.61 kPa和73.58 kPa；来流静温T分别为298 K和268 K。

1.4 数值计算结果

通过数值模拟得到三种不同头部形状的火箭弹模型以及三个不同尾舵面积的火箭弹模型在超音速下的俯仰气动特性。

1.4.1 头部形状对俯仰特性的影响

图4给出了Ma=3.0时三个模型俯仰力矩系数的变化规律，从图中可以看出三个模型俯仰力矩系数(绝对值)随攻角的变化规律基本相同，均随攻角的增大而增大。在负攻角区域，正俯仰力矩使原本处于低头状态的模型有抬头趋势；反之，在正攻角区域，负俯仰力矩使原本处于抬头的模型有低头趋势。在0°攻角附近，模型的俯仰力矩为零，这是由于模型的对称布置所致。PM模型的俯仰力矩系数(绝对值)始终最大，CM次之，DM最小。图5给出了Ma=3.0时三个模型的压心系数随攻角变化曲线，可以看出PM模型的压心系数最大，CM次之，DM最小，说明了PM模型的压心最靠后，稳定性较好。

图4 Ma=3.0时模型Cm随α变化曲线

图5 Ma=3.0时模型Xcp/l随α变化曲线

1.4.2 尾舵面积对俯仰特性的影响

图6给出了Ma=4.0时，CR、CM、CN模型俯仰力矩系数随攻角变化曲线。从图中可以看出：三个模型的俯仰力矩系数随攻角变化规律基本一样，俯仰力矩系数(绝对值)都随攻角的增大而增大。CN模型的俯仰力矩系数(绝对值)始终最大，CM次之，CR最小。图7给出了Ma=4.0时，三个模型的压心系数随攻角变化曲线，CN模型压心最靠后，CM次之，CR最靠前，说明固定头部的火箭弹模型，尾舵面积越大，稳定性越好。

图6 Ma=4.0时模型Cm随α变化曲线

2 计算结果与实验结果对比

图8给出了CM模型风洞实验与数值计算分别得出的俯仰力矩系数曲线对比，可以看出二者的数值非常接近，误差均在10%以内。

图7 Ma=4.0时模型Xcp/l随α变化曲线

图8 CM模型俯仰力矩系数随攻角变化曲线

3 各部件对俯仰气动特性影响分析

3.1 头部形状影响俯仰特性变化机理

为探究头部形状影响火箭弹模型俯仰特性的原因，通过分析模型各部件对全弹气动力的贡献解释。

图9给出了C、D、P型头部在Ma=3.0，4°攻角下Z=0截面上的压力云图。可以看出双锥形头部激波强度较单锥形大，气流流经双锥形头部第二段锥面产生膨胀波使得压力减小，因此压力分布在第一段锥面的比重较大，压心位置靠前。

双锥型头部D型的第一段锥面比C型长，且压力分布在第一段锥面的比重较大，因此D型的压心位置最靠前。由于质心位于压心之后，综合比较可推导出：作用在头部的法向力力矩臂(头部压心到质心的距离)D型>C型>P型。

图9 Ma=3.0，4°攻角下三个头部的压力云图

表1给出了在Ma=3.0时C、D、P型头部在不同攻角下提供的法向力。可以看出，三个头部所提供的法向力随攻角的增大而增大，大小依次是D型>C型>P型。

表1 Ma=3.0时C、D、P头部不同攻角提供的法向力

综合图9和表1可知：头部所提供的俯仰力矩(反转力矩)大小依次是：D型>C型>P型。

表2给出了CM、DM、PM模型的尾舵在Ma=3.0时在不同攻角下俯仰力矩系数。可以看出，三个模型尾舵的俯仰力矩系数(绝对值)都随攻角增大而增大，大小依次是：wingPM>wingDM>wingCM。

表2 Ma=3.0时三个模型尾舵俯仰力矩系数

综合以上分析可知，DM模型的头部提供俯仰力矩(反转力矩)最大，尾舵提供的俯仰力矩最小；而PM模型中头部提供的俯仰力矩(反转力矩)最小，尾舵提供的俯仰力矩最大。因此对于全弹而言，PM模型的俯仰力矩系数最大，CM次之，DM最小。

3.2 尾舵面积影响俯仰特性变化机理

图10给出了Ma=4.0时，三个尾舵R型、M型、N型提供的法向力系数随攻角的变化曲线，可以看出法向力大小随攻角的增大而增大，近似呈线性规律，舵面积最大的N型提供的法向力最大，舵面积最小的R型提供的法向力最小。依次是N型>M型>R型。

图10 R、M、N型尾舵CN随α变化曲线

图11给出了在Ma=4.0时，R、M、N型尾舵压心系数随攻角变化的曲线，由图中可以看出：三个尾舵的压心系数随攻角变化的规律一样，R型的压心系数始终最大，M型次之，N型最小，由此可得出三个尾舵俯仰力矩臂的大小依次是：N型>M型>R型。

图11 R、M、N型尾舵Xcp/l随α变化曲线

综合分析图10和图11可得到如下结论：三个尾舵提供的俯仰力矩大小是N型>M型>P型。

表3给出了CR、CM、CN三个模型的头部在Ma=4.0时俯仰力矩系数随攻角的变化。可以看出，三个模型的头部俯仰力矩系数都随攻角的增大而增大，数值大小依次是：noseCR>noseCM>noseCN。因此可得出头部提供的反转力矩大小依次是：noseCR>noseCM>noseCN。

综合以上的分析可得，CN模型头部提供的俯仰力矩(反转力矩)最小，而尾舵提供的俯仰力矩最大，因此全弹的俯仰力矩最大，CR模型头部提供的俯仰力矩(反转力矩)最大，而尾舵提供的俯仰力矩最小，因此全弹的俯仰力矩最小。

表3 Ma=4.0时三个模型头部俯仰力矩系数

4 结论

1) 超音速下，无翼式布局火箭弹俯仰力矩随攻角的增大而增大；随着马赫数的增大，同一模型的俯仰力矩有减小的趋势。

2) 无翼式布局头部形状对俯仰气动特性有较大的影响，双锥形头部比单锥形头部有更大的法向过载。而单锥型头部比双锥形头部有更好的稳定性，双锥形头部减小第一段锥面长度能提高稳定性。

3) 增大尾舵面积能增大尾翼的法向过载和全弹的稳定性。

[1] 雷娟棉,居贤铭,苗瑞生.多片尾翼布局弹箭气动特性数值计算[J].北京理工大学学报,2003,23(6):686-689.

[2] 陈刚,董超,苏伟,等.弹翼对战术弹压心变化范围影响分析[C]//北京力学会第19届学术年会论文集,2013.

[3] 张延成.尾翼火箭弹流场数值研究[D].太原：中北大学,2011.

[4] 倪金付.正常式布局制导火箭弹气动布局研究[D].南京：南京理工大学,2015.

[5] 刘德广.大攻角超音速无翼式导弹舵面法向力工程算法[C]//首届全国航空航天领域中的力学问题学术研讨会论文集 (上册),2004.

[6] MAVRIPLIS D J,JAMESON A.Multiplied solution of the Navier-Stokes equations on triangular meshes[J].AIAA Journal,1990,28(8):1415- 1425.

[7] SPALART P,ALLMARAS S.An equation turbulence model for aerodynamic flows[R].AIAA 92- 04139,1992.

[8] FRÖHLICH J,VON TERZI D.Hybrid LES/RANS methods for the simulation of turbulent flows[J].Progress in Aerospace Sciences,2008,44(5):349-377.

(责任编辑 周江川)

Effects of Nose Shape and Tail Rudder Area on Pitch Aerodynamic Characterics for Missile

NI Man, CHEN Shao-song, ZHANG Jing-chao

(Nanjing University of Science & Technology， Nanjing 210094, China)

Numerical simulation and wind tunnel test are used to analysis pitch aerodynamic characteristics of wingless rocket model with different heads and tail rudder area under supersonic condition.In a conclusion, wingless rocket with single conical nose has better stability than double conical nose in the condition of fixed slenderness ratio, and wingless rocket with bigger tail rudder area has a better performance of overload and stability.which provides the guildance of aerodynamic configuration layout for wingless missile.

wingless type;missile;nose shape;tail rudder area;aerodynamic characteristic

2017-01-17；

2017-02-25 作者简介：倪曼(1990—)，女，硕士研究生，主要从事弹箭气动布局方面研究。

陈少松(1958—)，男，研究员，主要从事空气动力学、弹箭气动布局方面研究。

10.11809/scbgxb2017.05.013

format:NI Man, CHEN Shao-song, ZHANG Jing-chao.Effects of Nose Shape and Tail Rudder Area on Pitch Aerodynamic Characterics for Missile[J].Journal of Ordnance Equipment Engineering,2017(5):56-60.

TJ415

A

2096-2304(2017)05-0056-05

本文引用格式：倪曼，陈少松，张鲸超.头部和尾舵布局对弹箭俯仰气动特性影响[J].兵器装备工程学报，2017(5):56-60.