正则化多任务学习的快速算法*

史荧中，汪菊琴，许 敏，王士同

1.江南大学 数字媒体学院，江苏 无锡 214122

2.无锡职业技术学院 物联网学院，江苏 无锡 214121

正则化多任务学习的快速算法*

史荧中1,2+，汪菊琴1,2，许 敏1，王士同1

1.江南大学 数字媒体学院，江苏 无锡 214122

2.无锡职业技术学院 物联网学院，江苏 无锡 214121

SHI Yingzhong,WANG Juqin,XU Min,et al.Fast algorithm for regularized multi-task learning.Journal of Frontiers of Computer Science and Technology,2017,11(6)：988-997.

正则化多任务学习（regularized multi-task learning，rMTL）方法及其扩展方法在理论研究及实际应用方面已经取得了较好的成果。然而以往方法仅关注于多个任务之间的关联，而未充分考虑算法的复杂度，较高的计算代价限制了其在大数据集上的实用性。针对此不足，结合核心向量机（core vector machine，CVM）理论，提出了适用于多任务大数据集的快速正则化多任务学习（fast regularized multi-task learning，FrMTL）方法。FrMTL方法有着与rMTL方法相当的分类性能，而基于CVM理论的FrMTL-CVM算法的渐近线性时间复杂度又能使其在面对大数据集时仍然能够获得较快的决策速度。该方法的有效性在实验中得到了验证。

多任务学习；大数据集；核心向量机；快速分类

1 引言

近期的研究[1-6]表明，较之于单独学习各个子任务，对多个相关子任务同时学习能有效地提升预测性能。事实上，当同时学习多个复杂的任务时，从其他任务中获取的信号能作为非常有益的归纳信息[1-2]。学者们从多任务分类[2-7]、聚类[8-10]、回归[11-13]、特征选择[14-15]等方面展开了研究，并在网页标注、人脸识别、年龄估计、语音与图像处理、疾病预测、生物医学等[16-18]多个应用领域都取得了丰富的成果。一致性原理[19-20]又对此现象给出了理论保障，即若最大化各相关子学习机的一致性，则能使各子学习机的性能得到改善[19-22]。

多任务学习研究的角度之一，是子任务之间的相关结构。Evgeniou等人提出了正则化多任务学习（regularized multi-task learning，rMTL）[6]方法，其核心思想是多个子任务呈团状分布，共享同一个中心。随后，学者们从实践应用的角度出发，研究了在应用领域特别是生物医学方面，当子任务之间呈现出较清晰的图状关联和树状关联时的多任务学习方法。Friedman等人依据实际应用中蛋白质组之间存在特定的图状结构，对蛋白质组的信号进行了分析[16]。Chen等人基于子任务之间的图结构，进行了果蝇基因表示图的自动标记[17]。Widmer等人利用了生物之间特定的树状及图状关联进行了真核生物的生物序列分析[18]。也有学者将多任务学习方法推广到其他方面，如多类多任务学习方法[7]等。其中，rMTL方法以其模型的简洁性而成为多任务学习理论研究的基础，并扩展出许多其他方法。

虽然各种多任务学习方法在理论及实践中都已经取得了较好的成果，但当前社会信息化的发展对多任务学习提出了新的挑战。随着大数据时代的来临，社交信息及生物基因信息越来越庞大，多任务学习算法的时间及空间复杂度也越来越彰显其重要性。作为其他多任务学习方法的基石，rMTL方法的对偶问题等价于核空间中的另一支持向量机（support vector machine，SVM）问题，其算法时间复杂度一般情况下为O(n3)，其中n为问题空间中的样本容量。即使采用序贯最小化[23]方法来求解rMTL的对偶问题，使其复杂度降为O(n2.3)，rMTL在面对大数据集时仍有很大的局限性。而最近面向数据流的研究[24]虽然能快速求解多个子任务，但其模型并不能直接应用于多任务学习领域。如何寻找出一种新的多任务学习方法，既能保持rMTL方法良好的特性，又能在面对大数据集时有较好的时间性能，正是本文的出发点。

结合前期在数据流领域的研究基础[24]，本文提出了快速正则化多任务学习（fast regularized multi-task learning，FrMTL）方法，并基于核心向量机[25]（core vector machine，CVM）理论给出了FrMTL方法的快速算法（fast regularized multi-task learning core vector machine，FrMTL-CVM）。所提FrMTL方法及其快速算法FrMTL-CVM具有以下特点：

（1）FrMTL方法采用了与rMTL方法相同的理念，即在特征空间中共享同一个矢量。在分类性能上，FrMTL方法与rMTL方法相当。

（2）FrMTL方法可依据CVM理论[25]设计出快速算法FrMTL-CVM，以应对多任务大数据集问题，其渐近时间复杂度与样本总容量n呈近线性关系。

本文组织结构如下：第2章介绍rMTL方法及其他相关工作；第3章研究FrMTL方法；第4章讨论核心向量机及FrMTL方法的快速算法；第5章为实验结果与分析；第6章总结全文。

2 相关工作

多任务学习：假设有T个学习任务，每个任务中的样本点取自于空间X×Y，X⊂ℝd,Y⊂ℝ。每个任务中包含m个样本点{(x1t,y1t),(x2t,y2t),…,(xmt,ymt)}，其概率分布Pt是不同的。多任务学习的核心思想是同时求解T个任务，利用其他相关任务中的有效信息来提高学习所得模型的泛化能力。

Evgeniou等人在2004年提出了正则化多任务学习方法[6]，在保持各个子学习机局部优化的同时，使多个学习机之间的全局差异最小化。他们认为，多个子任务的决策模型应该是相似的，并共享核空间中的某个公共矢量，每个子任务的决策模型wt由公共矢量w0与偏差量vt构成，即wt=w0+vt。rMTL方法的目标函数如下：

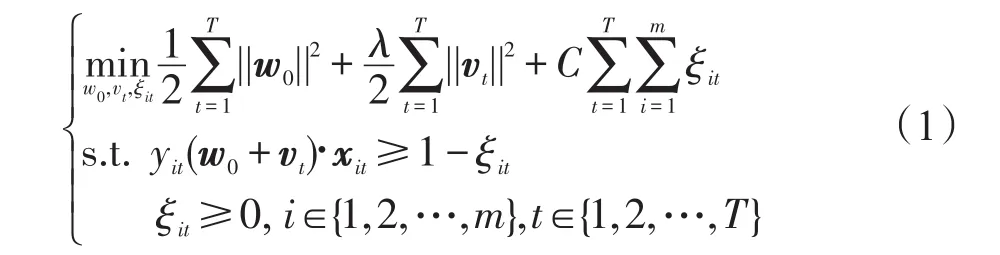
参照文献[6]，rMTL方法原始问题的对偶问题为如下二次规划问题：

其中，i∈{1,2,…,m}，t∈{1,2,…,T}，K(x,·)为扩展核空间中的某个核函数。其决策函数为：

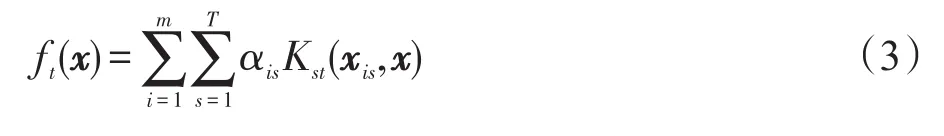
由式（2）可知，rMTL方法的对偶问题为核空间中的SVM问题，求解的时间复杂度为O(n3)，其中n为问题空间中的样本容量。即便采用序贯最小化[23]（sequential minimal optimization，SMO）方法来求解rMTL的对偶问题，使其复杂度降为O(n2.3)，也很难适应大数据时代的算法性能需求。

为了将rMTL方法推广到更多的实践应用上，Widmer[18]和Chen[17]等人依据子任务之间呈现不同的结构，设计出了Tree-MTL方法及Graphical-MTL方法。其中Tree-MTL方法是为了更好地进行生物序列分析，利用了第t个模型wt与它的父模型wparent(t)之间的相关性，假设可以通过最小化它们的差异||wt-wparent(t)||使子模型与父模型相互增益[18]：

Friedman等人依据实际应用中蛋白质组之间存在特定的图状结构，对蛋白质组的信号进行了分析[16]。2013年，Chen等人提出了改进型交互结构优化（improved alternating structure optimization，iASO）方法[17]，利用果蝇基因之间呈图状结构的特性，对基因进行自动标记。

树状多任务学习模型及图状多任务模型向实用方向变化，但子任务之间存在的复杂关联给计算带来了一定的麻烦，因而在面向较大规模数据集时，计算时间得不到保障。iASO虽然解决了局部最优化问题，但只适用于小样本数据集[17]。

Shi等人在针对数据流的分类研究中，提出了ITA-SVM方法[24]。该方法能同时求解多个子任务，当应用于较大规模数据集时，算法的渐近时间复杂度接近于O(n)。但该方法只适用于多个子任务呈序列状分布的情形，并不能直接应用于传统的多任务学习情形。

3 快速正则化多任务学习方法FrMTL

鉴于以往MTL方法在针对较大规模数据集时的复杂度瓶颈，本文结合ITA-SVM[24]的思路，提出了与rMTL方法分类能力相当，且具有快速处理多任务大数据集能力的FrMTL方法。对子任务之间具有树状及图状结构的场景，由于子任务之间的耦合带来了模型及计算上的较大差异，将另文表述其快速算法。

FrMTL方法有着与rMTL方法及ITA-SVM方法相同的策略，即基于共享矢量协同求解多个子任务。为使FrMTL方法能进一步用快速算法求解，本文按文献[24-27]的方法对式（1）略作改变，引入分类间隙ρ，通过推导可得到适于对多任务大数据集进行快速求解的对偶形式。FrMTL方法的目标函数为：

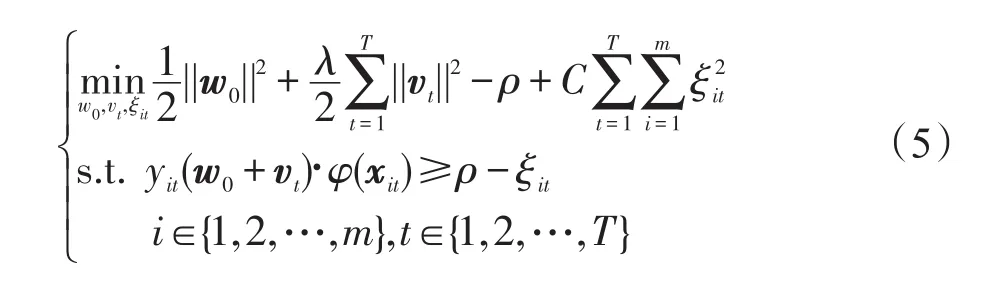
通过推导，不难得到式（5）的对偶问题如下：

其中：

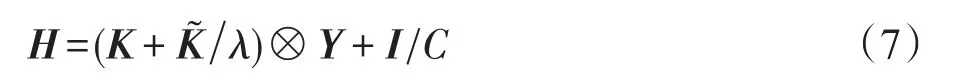
K=[Kis,jt]N×N,Kis,jt=φ(xis)Tφ(xjt)，φ为核函数

I为单位矩阵，α=(α11,α21,…,αm1,…,α1T,α2T,…,αmT)T

由式（6）、（7）可知，FrMTL问题的对偶形式等价于核空间中的另一SVM问题，其时间复杂度为O(n3),采用SMO方法求解的时间复杂度为O(n2.3)，与rMTL方法相比，其时间性能并无本质的变化。但当借助核心向量机技术快速求解时，式（6）的时间复杂度及空间复杂度可降为O(n)。

4 核心向量机及FrMTL方法的快速算法

4.1 核心向量机

最小包含球（minimum enclosing ball，MEB）问题[28]可以转化为二次规划问题的矩阵形式：

其中，α=[α1,α2,…,αn]T为Lagrange乘子；Kn×n=[k(xi,xj)]=[ϕ(xi)Tϕ(xj)]为核矩阵。diag(K)表示由核矩阵K的主对角线元素组成的向量。

考察核函数中的特殊情形，即核矩阵对角元素恒为常数：

Tsang等人在文献[25]中指出，形如式（8）且满足式（9）的二次规划问题，均等价于求解MEB问题。他们在此基础上开发了核心向量机（core vector machine，CVM），CVM算法对于处理大规模数据集发挥了惊人的效果。对不满足式（9）的形如式（8）的二次规划问题，也可以使用核心集方法进行快速求解，给核空间中任意样本点ϕ(xi)附加一维新特征δi∈R，形成新特征空间中的新样本使其满足MEB问题的式（9）条件，然后求解在新特征空间中的最小包含球。对该最小包含球增加一个约束条件，即最小包含球中增加的特征维对应的中心固定在原点，即中心为这里c为原特征空间中的最小包含球球心。该问题的标准形式如下：

4.2 FrMTL-CVM算法描述

FrMTL方法的求解是一个普通的二次规划问题，其求解时间复杂度为O(n2)~O(n3)，对于大数据集来说应是相当可观的计算开销。仔细观察式（6），它可以转化为形如式（11）的MEB问题。因此，FrMTL方法可以利用核心向量机技巧来求解。并且MEB问题的求解过程中，只需要计算核心集之外的点到核心集的距离，无需计算所有点之间的相互距离，因此不必预先计算核矩阵H，这就使FrMTL方法能用快速算法求解。

可以将式（6）等价地改写如下：

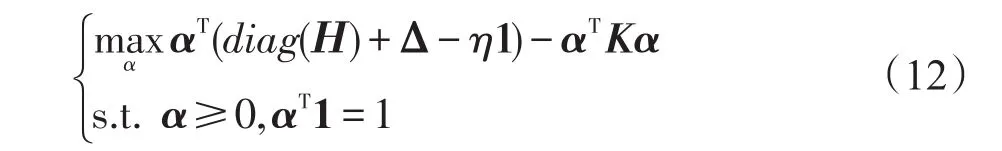
这是一个MEB问题，其中Δ=-diag(H)+η1，通过调节常数η的值，使Δ≥0。

FrMTL-CVM算法的输入为大数据集S，核心集逼近精度ε及η、Δ等参数；输出为核心集St和权重系数α。下面给出实现步骤：

（1）初始化核心集S0，最小包含球中心c0，半径R0，迭代次数t=1。

（3）在扩展的特征空间中找到离ct最远的点x,加入核心集，使得St+1=St⋃x。

（4）对新的CCMEB进行求解，得到新的球心ct+1和半径Rt+1，权重系数α；计算新的球心到其他各点的距离；t=t+1，转（2）。

（5）终止训练，返回核心集St，权重系数α。

在实践中发现，如果η取值较大，则FrMTLCVM算法收敛速度就非常快，所得到的核心集数量较少，实验精度也随之而降低。对FrMTL-CVM算法而言，如果选用高斯核作为核函数，可以更容易预估η的合理取值。

从本质上来讲，FrMTL-CVM算法是基于MEB近似算法的一个特例，因此在衡量系统开销时，有关核心集的结论适用于FrMTL-CVM算法。本文根据参考文献[24-27]，直接给出相似的性质。

性质1对于给定的近似误差ε，由FrMTL-CVM算法求得的核心集数量的上界为O(1/ε)，算法迭代次数的上界为O(1/ε)，求得的支持向量数量上界为O(1/ε)。

性质2对于给定的误差ε，FrMTL-CVM算法的时间复杂度的上界为O(N/ε2+1/ε4)。

5 实验结果与分析

鉴于rMTL方法[6]的良好性能，且它是众多扩展方法的基础，本文将其作为实验参照，以评估FrMTL方法及FrMTL-CVM快速算法。实验将从两方面进行：首先需要验证FrMTL方法的分类性能是否与rMTL方法相当，因FrMTL方法保持良好的分类性能是其快速算法有效的前提；其次需要验证FrMTL-CVM在面对大数据集时是否具有较好的时间效率，且其时间性能是否与CVM理论相符。

人生就是一条路，在起跑线的起点，所有的人都整装待发，但能跑到最后的那些人都是最能坚持的，他们才是最成功的。在奔跑的路上，我失掉了坚持，迷茫、无助都向我逼近，我几乎接近崩溃的边缘。找回坚持，是一个崭新的开始。

5.1 实验设置

5.1.1 实验平台信息

实验环境：操作系统为WindowsXP；处理器为奔腾1.87 GHz；内存为4 GB；主要应用软件为Matlab R2010a。

5.1.2 所用方法

表1列出了下文实验的各个算法名，并列出了相关算法中的主要参数。表1中的参数ε仅指CVM算法中的近似程度，而求解二次规划问题时的精度参数不再列出，都取默认值ε′=1E-6。

Table 1 Methods and parameters in experiments表1 实验中各种算法及主要参数

5.1.3 实验数据

为了验证FrMTL方法的适应能力，本文将在模拟数据集及真实数据集上展开实验。模拟数据集以数据集DS0为基础来生成，DS0包含3个子任务，共300个样本点，每个子任务正负类样本均为50。其中子任务T1的正类中心(0,0)，方差为1，负类中心(2.5, 0)，方差为1；子任务T2的正类中心(0,0)，方差为1，负类中心(2.5,0)，方差为1；子任务T3的正类中心(0, 0)，方差为1.1，负类中心(2.5,0)，方差为1.1。模拟数据集基于DS0生成，由DS0中的子任务经过不同程度的旋转、平移来模拟子任务之间不同的相关性。数据集DS1中的Task1直接采用DS0中的T1，Task2为T2进行一定的旋转（Rotate=5°）而生成，Task3为T3进行一定的平移（Move=0.05）而生成。DS2~DS6中的子任务Task1都取为DS0中的T1，Task2、Task3则由DS0中的T2加大旋转量，T3增加平移量而生成。模拟数据集DS1~DS6，以及用于评估算法时间性能的数据集DS7的具体描述如表2所示。

5.1.4 实验参数的设置

为了客观地评估各种方法的分类性能，在每个数据集上，本文除训练样本外，还独立生成了相同分布的测试样本。训练样本和测试样本各有10组，共进行10次重复实验，以尽量减少因模拟数据的随机性而带来的不客观性。实验分为两个阶段：第一阶段是针对训练样本，优化各方法的系统参数；第二阶段是根据前一阶段得到的参数设置对训练样本建模，使用测试样本来评估各方法的分类性能。优化系统参数时采用网格遍历法，其中参数C的遍历范围是10[-2,…,2]；参数λ的遍历范围是10[-2,…,2]；本文选取使用最广泛的高斯核，其核带宽取值为2[-2,…,5]。

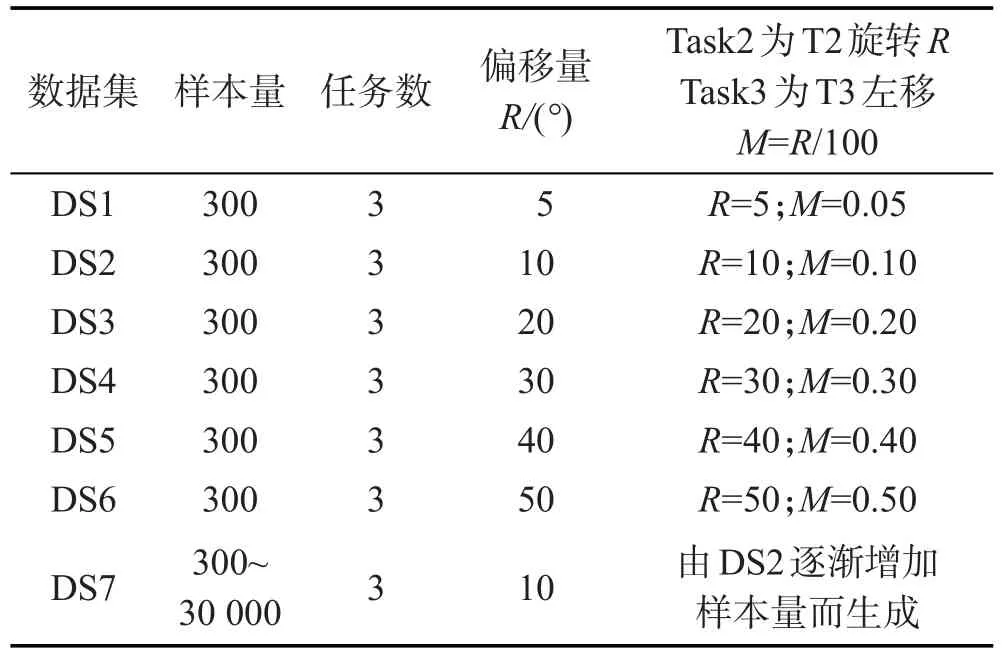
Table 2 Description of artificial datasets表2 实验所用人工数据集

5.2 FrMTL方法的分类能力

本阶段将对FrMTL方法进行分类准确率的评估。用于实验对比的其他方法分别为：（1）对每个任务分别用SVM方法独立求解，记为SVMs；（2）rMTL方法。其中FrMTL-CVM指的是用核心向量机求解FrMTL相应的二次规划问题。

在数据集DS1~DS6上，按照实验流程，对每个对比方法都进行10次重复实验。在每个数据集上，求得对各个子任务的分类准确率及标准差，如表3所示。图1显示的是当子任务之间的偏移量逐渐变大时，也即在数据集DS1~DS6上，各个对比方法在每个数据集上3个子任务的平均准确率。

由表3和图1可以得到如下结论：

（1）从表3中可以看出，当采用多任务方式同时求解3个相关子任务时，rMTL方法和FrMTL方法及其快速算法FrMTL-CVM的分类性能远优于用普通SVM方法单独求解各个子任务。

（2）对比表3中的rMTL方法和FrMTL方法及其快速算法FrMTL-CVM，在6个数据集的共18个子任务的求解中，rMTL方法在7个子任务的求解中取得了较好的效果，FrMTL方法在10次子任务的求解中取得了较好的效果，而快速算法FrMTL-CVM在求解3个子任务时有较好的效果。因而FrMTL方法的分类能力与rMTL方法是可比较的。而FrMTL-CVM方法与rMTL方法也是相当的。

Table 3 Classification accuracy and deviation on DS1~DS6表3 在数据集DS1~DS6上各方法的平均准确率及标准差

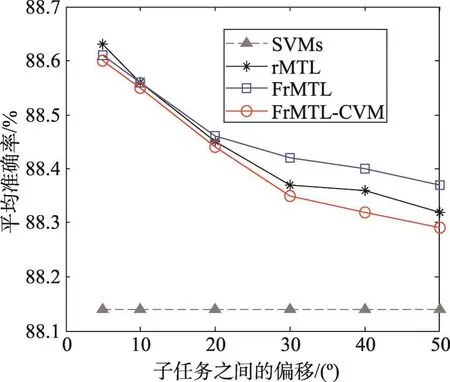
Fig.1 Accuracy with different rotations in sub-task图1 随子任务之间偏移程度的增加各方法的准确率

（3）由图1可知，随着子任务之间偏移量变大，rMTL方法和FrMTL方法的分类性能缓慢下降，但仍然优于采用SVM方法单独求解各子任务。另外，当子任务之间关联较强时，rMTL方法和FrMTL方法的分类性能完全相当，而当子任务之间关联较弱时，这两个方法的分类能力仍然是相当的。快速算法FrMTLCVM的分类能力与rMTL方法及FrMTL方法总体上是相当的。

5.3 FrMTL方法的时间性能

鉴于在数据集DS2上，rMTL方法和FrMTL方法的分类性能非常接近，本文以数据集DS2为基础，逐渐增加训练样本及测试样本的容量，以此来评估各方法的时间效率。各数据的容量依次为300，600，1 500，3 000，6 000，15 000，30 000。同样独立生成10组训练样本及测试样本，并将各方法在不同容量样本上的平均准确率与标准差、平均训练时间及标准差分别报告在表4及表5中（其中—表示在本文实验环境中无法得到相应结果）。为了能更清晰地分析随数据量增加各方法的时间性能，以lgn（n为样本量）为横坐标，lgS（S为运行时间，单位为s）为纵坐标绘制各方法的时间性能图，将指数曲线转化为近线性曲线，斜率代表指数量级，如图2所示。

Table 4 Classification accuracy and deviation with different dataset sizes表4 各方法在不同数据量下的平均分类准确率及标准差

Table 5 Training time and deviation with different dataset sizes表5 各方法在不同数据量下的平均训练时间及标准差

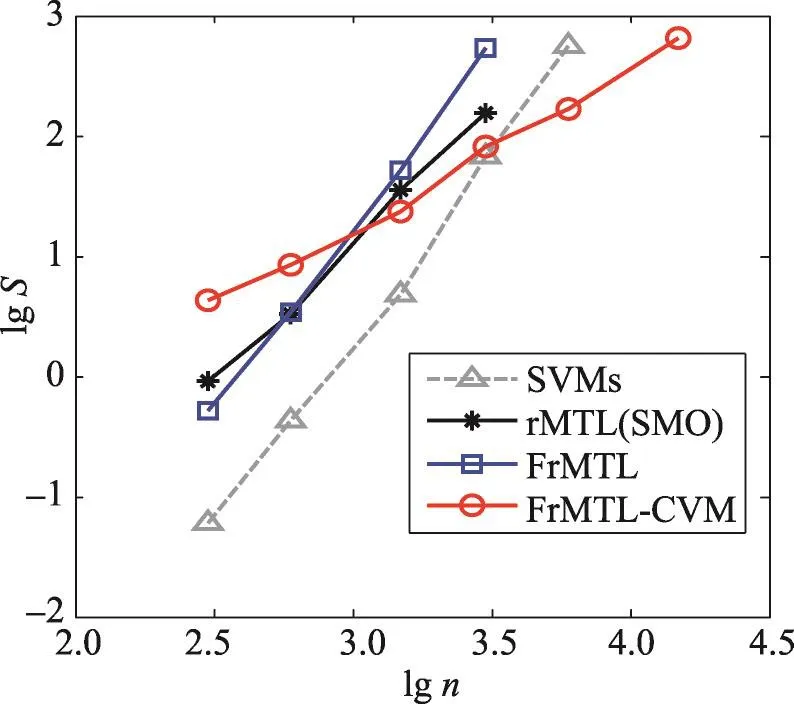
Fig.2 Training time with different dataset sizes图2 随训练样本量的增加各方法的训练时间

从表4、表5及图2可以得到如下结论：

（1）从表4中可以看出，随着训练数据量的增加，各方法的分类性能逐渐增高，其中FrMTL方法及其快速算法FrMTL-CVM的分类性能与rMTL相当，都优于用普通的SVM方法单独求解各个子任务。同时，普通的SVM方法及rMTL方法、FrMTL方法都需要预先计算核矩阵，因此相应方法受硬件约束较大，当数据量较大时，相应方法无法继续求解。而FrMTLCVM无需预先计算核矩阵，能对较大容量的数据集进行训练，因而能得到泛化能力更强的模型。

（2）从表5中可以看出，在数据量较小时，FrMTLCVM方法在求解时间上并无优势，但随着数据量的增加，FrMTL-CVM的求解时间缓慢增加，明显优于普通二次规划的求解。

（3）由图2可知，当采用普通SVM方法求解时，随着数据量的变化，SVMs及FrMTL方法所用时间具有相同的趋势，准直线的斜率接近于3，显示出用普通方法求解二次规划问题时的O(n3)时间复杂度。当用SMO方法求解rMTL问题时，斜率略大于2，与其O(n2.3)的理论时间复杂度一致。而采用CVM方法求解的FrMTL-CVM算法所用时间的准直线的斜率趋势略大于1，与其理论上的近线性时间复杂度相符，时间性能远优于SMO方法。当然，FrMTL-CVM方法训练所用时间的稳定性并不算好，其原因是当用CVM方法求解时，不同数据集上求解所得的支持向量数目可能有较大差异，由此造成了求解时间的波动性较大。但总体而言，FrMTL-CVM算法的时间性能得到保障，其时间复杂度的上界为O(n/ε2+1/ε4)，ε为设定的近似误差。

由实验可知，FrMTL方法的分类性能与rMTL方法相当，采用快速方法求解的FrMTL-CVM方法在分类性能上并无很大变化，仍然与rMTL方法相当。而当数据量较大时，FrMTL-CVM方法的处理能力及其时间性能远优于其他方法。

6 结束语

本文提出了面向多任务学习的快速正则化多任务学习方法FrMTL。由于借鉴了rMTL方法及ITASVM方法中共享矢量的思想及兼顾局部优化和全局优化的优点，FrMTL方法的分类性能与rMTL方法是等价的。而FrMTL-CVM方法良好的时间性能使面对多任务大数据集时仍能获得相对较快的决策速度。当然FrMTL方法仍需要进一步研究以适应更多的应用场景，特别是当多个子任务呈网状分布或树状分布时，如何解决此类更复杂耦合关系带来的矩阵求逆问题，将是更有意义的挑战。

[1]Caruana R.Multitask learning[J].Machine Learning,1997, 28(1):41-75.

[2]Baxter J.A model of inductive bias learning[J].Journal of Artificial Intelligence Research,2000,12(1):149-198.

[3]Sun Shiliang.Multitask learning for EEG-based biometrics [C]//Proceedings of the 19th International Conference on Pattern Recognition,Tampa,USA,Dec 8-11,2008.Washington:IEEE Computer Society,2008:1-4.

[4]Yuan Xiaotong,Yan Shuicheng.Visual classification with multi-task joint sparse representation[J].IEEE Transactions on Image Processing,2012,21(10):4349-4360.

[5]Parameswaran S,Weinberger K.Large margin multi-task metric learning[C]//Advances in Neural Information Processing Systems 23:Proceedings of the 24th Annual Conference on Neural Information Processing Systems,Vancouver,Canada,Dec 6-9,2010.Red Hook,USA:Curran Associates,2011:1867-1875.

[6]Evgeniou T,Pontil M.Regularized multi-task learning[C]// Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Seattle, USA,Aug 22-25,2004.New York:ACM,2004:109-117.

[7]Ji You,Sun Shiliang.Multitask multiclass support vector machines:model and experiments[J].Pattern Recognition, 2013,46(3):914-924.

[8]Zhang Zhihao,Zhou Jie.Multi-task clustering via domain adaptation[J].Pattern Recognition,2012,45(1):465-473.

[9]Xie Saining,Lu Hongtao,He Yangcheng.Multi-task coclustering via nonnegative matrix factorization[C]//Proceedings of the 21st International Conference on Pattern Recognition,Tsukuba,Japan,Nov 11-15,2012.Washington:IEEE Computer Society,2012:2954-2958.

[10]Kong Shu,Wang Donghui.A multi-task learning strategy for unsupervised clustering via explicitly separating the commonality[C]//Proceedings of the 21st International Conference on Pattern Recognition,Tsukuba,Japan,Nov 11-15, 2012.Washington:IEEE Computer Society,2012:771-774.

[11]Wang Hua,Nie Feiping,Huang Heng,et al.A new sparse multi-task regression and feature selection method to identify brain imaging predictors for memory performance[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision,Barcelona,Spain,Nov 6-13,2011.Washington:IEEE Computer Society,2011:557-562.

[12]Solnon M,Arlot S,Bach F.Multi-task regression using minimal penalties[J].Journal of Machine Learning Research, 2011,13(3):2773-2812.

[13]Zhou Jiayu,Yuan Lei,Liu Jun,et al.A multi-task learning formulation for predicting disease progression[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Diego, USA,Aug 6-13,2011.New York:ACM,2011:814-822.

[14]Gong Pinghua,Ye Jieping,Zhang Changshui.Robust multi-task feature learning[C]//Proceedings of the 18th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Beijing,Aug 12-16,2012.New York:ACM,2012:895-903.

[15]Liang Yixiong,Liu Lingbo,Xu Ying,et al.Multi-task GLOH feature selection for human age estimation[C]//Proceedings of the 18th IEEE International Conference on Image Processing,Brussels,Belgium,Sep 11-14,2011.Washington:IEEE Computer Society,2011:565-568.

[16]Friedman J,Hastie T,Tibshirani R.Sparse inverse covariance estimation with the graphical lasso[J].Biostatistics, 2008,9(3):432-441.

[17]Chen Jianhui,Tang Lei,Liu Jun,et al.A convex formulation for learning a shared predictive structure from multiple tasks[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2013,35(5):1025-1038.

[18]Widmer C,Leiva J,Altun Y,et al.Leveraging sequence classification by taxonomy-based multitask learning[C]// LNCS 6044:Proceedings of the 14th Annual International Conference,Lisbon,Portugal,Apr 25-28,2010.Berlin,Heidelberg:Springer,2010:522-534.

[19]Luo Ping,Zhuang Fuzhen,Xiong Hui,et al.Transfer learning from multiple source domains via consensus regularization [C]//Proceedings of the 17th ACM Conference on Information and Knowledge Management,Napa Valley,USA,Oct 26-30,2008.New York:ACM,2008:103-112.

[20]Zhuang Fuzhen,Luo Ping,Xiong Hui,et al.Cross-domain learning from multiple sources:a consensus regularization perspective[J].IEEE Transactions on Knowledge and Data Engineering,2010,22(12):1664-1678.

[21]Jiang Yizhang,Chung F L,Ishibuchi H.Multi-task TSK fuzzy system modeling by mining inter-task common hidden structure[J].IEEE Transactions on Cybernetics,2015, 45(3):548-561.

[22]Zhang Minling.Research on multi-task learning[EB/OL]. (2011-08-10)[2016-01-30].http://www.paper.edu.cn/releasepaper/content/201108-156.

[23]Platt J C.Fast training of support vector machines using sequential minimal optimization[M]//Advances in Kernel Methods-Support Vector Learning.Cambridge,USA:MIT Press,1999: 185-208.

[24]Shi Yingzhong,Chung F L,Wang Shitong.An improved TA-SVM method without matrix inversion and its fast implementation for non-stationary datasets[J].IEEE Transactions on Neural Networks&Learning Systems,2015,25 (9):2005-2018.

[25]Tsang I W H,Kwok J T Y,Zurada J A.Generalized core vector machines generalized core vector[J].IEEE Transactions on Neural Networks Machines,2006,17(5):1126-1139.

[26]Qian Pengjiang,Wang Shitong,Deng Zhaohong,et al.Fast spectral clustering for large data sets using minimal enclosing ball[J].Acta Electronica Sinica,2010,38(9):2036-2041.

[27]Qian Pengjiang,Chung F L,Wang Shitong,et al.Fast graphbased relaxed clustering for large data sets using minimal enclosing ball[J].IEEE Transactions on Systems Man& Cybernetics:Part B Cybernetics,2012,42(3):672-687.

[28]Kumar P,Mitchell J S B,Yildirim E A.Approximate minimum enclosing balls in high dimensions using core-sets[J]. Journal of ExperimentalAlgorithmics,2003,8:1-29.

附中文参考文献：

[22]张敏灵.多任务学习的研究[EB/OL].(2011-08-10)[2016-01-30].http://www.paper.edu.cn/releasepaper/content/201108-156.

[26]钱鹏江,王士同,邓赵红,等.基于最小包含球的大数据集快速谱聚类算法[J].电子学报，2010,38(9):2036-2041.

SHI Yingzhong was born in 1970.He is a Ph.D.candidate at School of Digital Media,Jiangnan University,associate professor at Wuxi Institute of Technology,and the member of CCF.His research interests include artificial intelligence,pattern recognition,intelligent modeling methods and their applications.

史荧中（1970—），男，江南大学数字媒体学院博士研究生，无锡职业技术学院副教授，CCF会员，主要研究领域为人工智能，模式识别，智能建模及其应用。

WANG Juqin was born in 1982.She is an M.S.candidate at Department of Computer Science,Jiangnan University, and lecturer at Wuxi Institute of Technology.Her research interests include intelligent modeling methods and their applications.

汪菊琴（1982—），女，江苏吴江人，江南大学计算机系硕士研究生，无锡职业技术学院讲师，主要研究领域为智能建模及其应用。

XU Min was born in 1981.She is a post-doctor researcher at School of Digital Media,Jiangnan University.Her research interests include artificial intelligence,pattern recognition and their applications.

许敏（1981—），女，江苏无锡人，江南大学数字媒体学院博士后，主要研究领域为人工智能，模式识别及其应用。

WANG Shitong was born in 1964.He is a professor at School of Digital Media,Jiangnan University.His research interests include artificial intelligence,pattern recognition and bioinformatics.

王士同（1964—），男，江苏扬州人，江南大学数字媒体学院教授，主要研究领域为人工智能，模式识别，生物信息。

FastAlgorithm for Regularized Multi-Task Learning*

SHI Yingzhong1,2+,WANG Juqin1,2,XU Min1,WANG Shitong1
1.School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China
2.College of Internet of Things,Wuxi Institute of Technology,Wuxi,Jiangsu 214121,China
+Corresponding author:E-mail:shiyz@wxit.edu.cn

Regularized multi-task learning(rMTL)method and its extensions have achieved remarkable achievement in theoretical research and applications.However,previous research focuses on the relationship of tasks instead of the complexity of algorithms,the high computational cost of these methods are impractical for large scale datasets.In order to overcome this shortcoming,this paper proposes a fast regularized multi-task learning(FrMTL) based on core vector machine(CVM)theory.FrMTL is competitive with rMTL in classification accuracy while FrMTLCVM can make a decision rapidly for large scale datasets because of the merit of asymptotic linear time complexity. The effectiveness of the proposed classifier is also experimentally confirmed.

multi-task learning;large scale dataset;core vector machine;fast classification

2016-03,Accepted 2016-06.

A

TP391

*The National Natural Science Foundation of China under Grant No.61170122(国家自然科学基金面上项目);the New Century Excellent Talents Foundation from Ministry of Education of China under Grant No.NCET-120882(教育部新世纪优秀人才支持计划); the Top-Notch Academic Program of Jiangsu Higher Education Institutions under Grant No.PPZY2015C240(江苏省高校品牌专业建设工程资助项目).

CNKI网络优先出版:2016-06-23,http://www.cnki.net/kcms/detail/11.5602.TP.20160623.1401.016.html