两重稀疏约束的多标记社团分类算法*
2017-06-15潘志松任义强李国朋蒋铭初
李 娜,潘志松,任义强,李国朋,蒋铭初
1.中国人民解放军理工大学 指挥信息系统学院,南京 210007
2.中国电子科技集团公司 第三十二研究所,上海 201808
3.西门子电力自动化有限公司,南京 211100
4.西安通信学院,西安 710106
两重稀疏约束的多标记社团分类算法*
李 娜1,2,潘志松1+,任义强3,李国朋1,4,蒋铭初1
1.中国人民解放军理工大学 指挥信息系统学院,南京 210007
2.中国电子科技集团公司 第三十二研究所,上海 201808
3.西门子电力自动化有限公司,南京 211100
4.西安通信学院,西安 710106
LI Na,PAN Zhisong,REN Yiqiang,et al.Multi-label community classification method based on double sparse representation.Journal of Frontiers of Computer Science and Technology,2017,11(6):959-971.
在多标记研究中,对于标记间相关性的利用已经越来越广泛,从而标记关系的展示就很有必要。相对以往的研究而言,由于多标记数据的高维特征,在训练过程中极为繁琐耗时,稀疏优化就尤为关键;同时标记相关性的内涵没有经过深入挖掘,因此如何更方便有效地进行多标记分类以及研究所有标记之间的相关性显得尤为必要。提出了一种基于两重稀疏约束的多标记社团分类算法,该算法首先将ℓ1/ℓ2正则化应用到多标记数据的稀疏表示过程,为后面的研究提供便利条件;其次在多标记关系基础上应用基于ℓ1范数正则化的社团发现算法,有效地对标记进行社团划分,直观展示出标记关系的内涵。实验证明该方法能够快速、准确地进行多标记分类,并且能够准确展示标记关系。
多标记;标记关系;非负矩阵分解(NMF);ℓ1/ℓ2范数;ℓ1范数
1 引言
近年来,现实生活中的各式数据在不同领域构成了各种各样的网络,如人员关系网、邮件系统网络、分子结构网络等。不管是社会系统、信息系统,还是生物系统领域,这些网络都真实地存在于人们的社会生活中。如今人们对于网络的研究已经转向了实际的网络,实际网络通常由若干个社团组成,人们通过对社团的挖掘来获取网络中的隐含信息。与此同时,在现实生活中人们对于对象的研究也不断深化,往往将对象赋予多种标记,从而体现出对象的多重含义。比如对于一封邮件来说,它的内容可能同时包含了身份信息、个人情绪,以及与外界的相关联系;对于一个分子来说,它既可以按结构标识,亦可以按功能标识。因此,对于现实生活中的事物来说,它的标记同样具有关联,能够构成网络,形成某些社团。在多标记的研究中,一些标记对于对象来说可能并没有重要的相关性,比如文本预处理过程中词干的提取,一般文档库的文本中出现频率超过80%的词对检索过程根本不起作用[1],然而这些停用词却是出现最多的文字;又如在邮件系统Enron数据集[2]中,有些标记在53个标记中的作用远不如第45个标记——保密显得重要。因此,若能够找到一种稀疏方法,将不必要的标记过滤,同时找到最重要的标记信息,那么就能对多标记的社团结构进行更快的研究,并且找到社团中的骨干节点,这对于社团的含义描述有着重要的意义。
稀疏(sparsity)是最近几年机器学习和计算机视觉领域对于高维数据的研究热点之一[3]。也就是在一个足够大的训练样本空间内,对于一个类别的物体,可以大致地由训练样本中同类的样本子空间线性表示,因此当该物体由整个样本空间表示时,其表示的系数是稀疏的。当前对于数据的稀疏表示,是将稀疏方法应用于数据的降维预处理过程中,并在图像去噪、图像复原等方面取得了重大成功。通过稀疏可以得到数据最为重要的属性,然而对于标记的稀疏却没有找到合适的优化策略。
网络的社团结构[4]指相互之间具有比较大的相似性而与网络中的其他部分有着很大不同的节点的群。在社团内部,节点之间的联系非常紧密,社团之间的联系相对比较稀疏[5]。如在社会网络中,某一社团的人们与其他社团有着不一样的特质。对网络中节点寻找社团结构并对其进行分析是了解现实生活中各种网络组织的一种重要方法,并在多个领域有着重要的应用。然而社团结构在多标记数据集中的应用还不是很多,而多标记分类方法的应用却越来越广泛。在多标记分类算法中,现有算法已经越来越侧重于对标记间相互关系的利用,对于标记关系的获取形式也有多种[6],多标记之间的相关性同样可以构成具有标记节点关联的网络结构,并从该结构中分析标记之间隐含的相关信息。对待该网络结构,可以应用现有的社团发现算法进行分析。
目前在有效的社团组织发现方法中,非负矩阵分解(non-negative matrix factorization,NMF)[7-9]就是社团发现方法的一个非常有用的工具,与其他矩阵分解方法相比,NMF特殊之处在于其通过将非负性约束引入矩阵分解过程中,利用非负的低维矩阵对高维矩阵进行近似,这种约束会得到原始数据基于部分的表示,从而更好地反映原始数据的局部特征。若对标记所属社团矩阵进行稀疏优化,则标记的信息就会更明确,同时也能更好地理解标记之间的相关性。因此,对于多标记社团发现算法,也能够得到多标记的社团结构,明确每个标记社团的含义。本文在稀疏表示的基础上,针对多标记数据高维冗余特点,以及多标记社团稀疏性解释不强,矩阵效果不够完善,非负矩阵分解工作没有对标记之间的相互关系进行考虑,基于稀疏具有特征选择与可解释性的优点,对多标记的社团信息采用两重稀疏表示手段:由于多标记数据集属于高维数据,本身具有一定稀疏性,首先将稀疏优化应用到多标记数据集降维过程中,采用了ℓ1/ℓ2范数正则化[10-12]优化方法;其次在多标记的社团划分中采用了第二重的稀疏表示方法——ℓ1范数[13-15],目的是使得多标记社团划分结果更加明晰,社团分类能够更好地反映标记之间的相关性与无关性。
本文首先对两重稀疏约束的多标记社团分类相关工作进行介绍,随后详细说明了基于两重稀疏约束的多标记社团分类方法,并在已有数据集上将本文涉及内容与现有的一些方法进行对比,测试在多种实际数据集下的性能。最后进行总结。
2 相关工作介绍
2.1 多标记社团发现概念
现有的多标记工作对于标记相关性进行了充分的学习。由于样本数目较大,标记数量并不单一,标记间的关联不明显,目前已经有许多工作尝试挖掘和利用标记之间的关系。在现有多标记学习中,Huang等人在文献[6]中提出了多标记重用评分概念来有效反映标记之间的关联。该工作的多标记重用(multi-label hypothesis reuse,MAHR)算法中,根据标记间相互作用得到标记间的评分矩阵S,该矩阵可以量化成为多标记的关系矩阵,而社团分解中的NMF算法正是根据节点间的关系矩阵对节点进行划分。由于现有多标记学习工作并未明确指出多标记社团结构内涵,同时稀疏的社团结构对多标记工作的意义也有待探索,于是本文希望能够利用NMF算法挖掘出多标记关系矩阵并揭示多标记的社团结构,对标记的社团结构作出明确解释,使得对多标记关系的研究更清晰且有意义。
2.2 非负矩阵分解
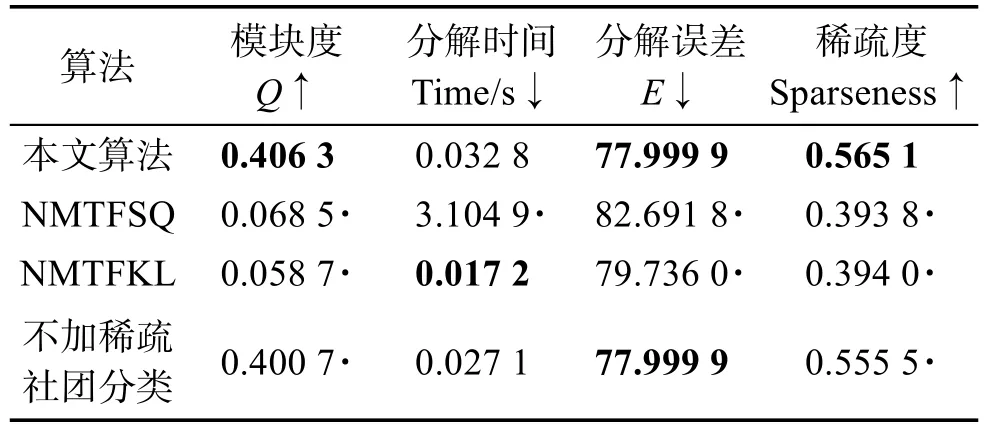
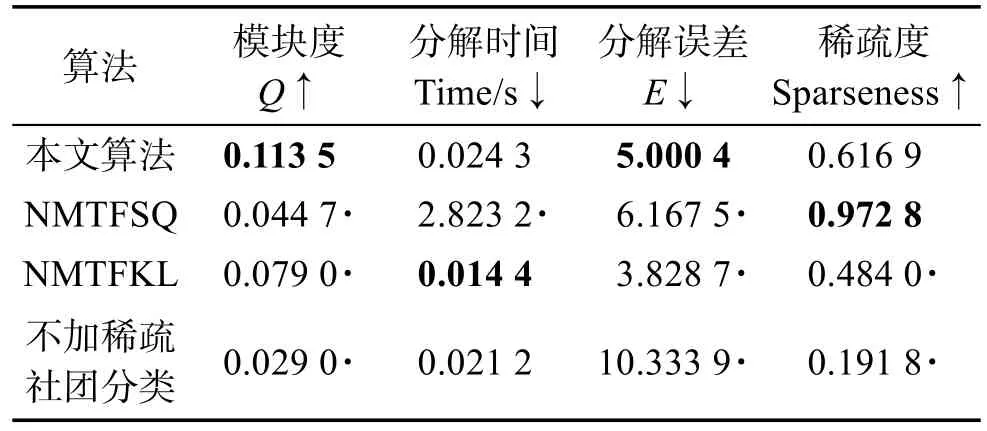
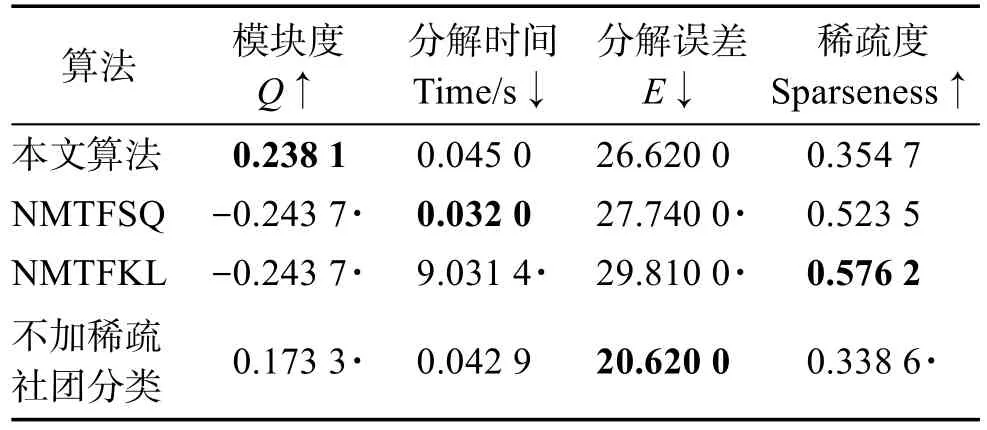
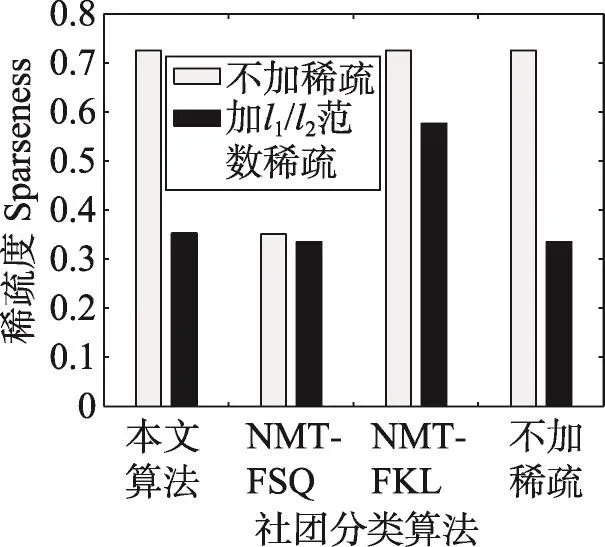
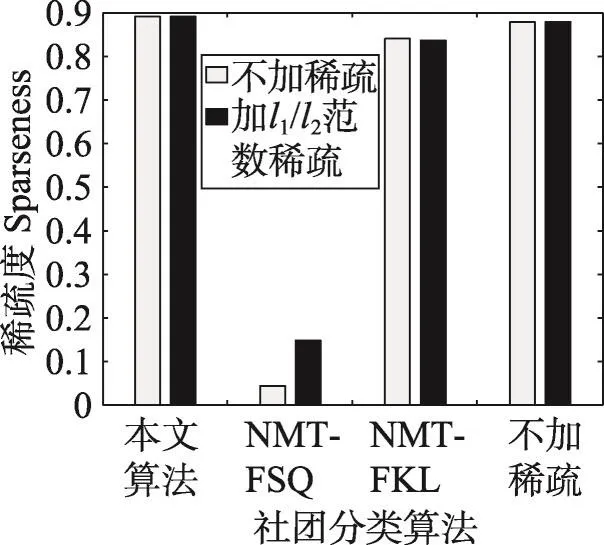
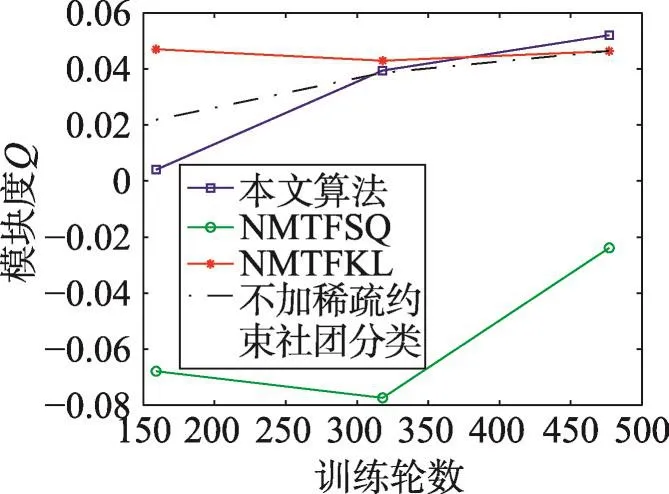
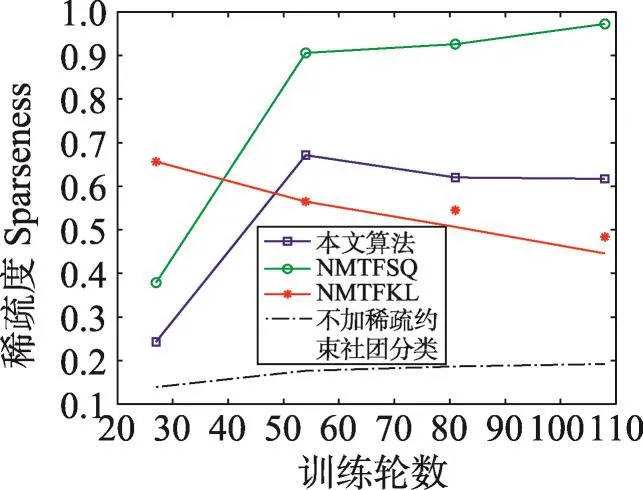
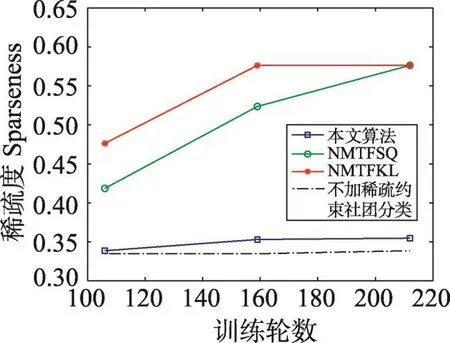
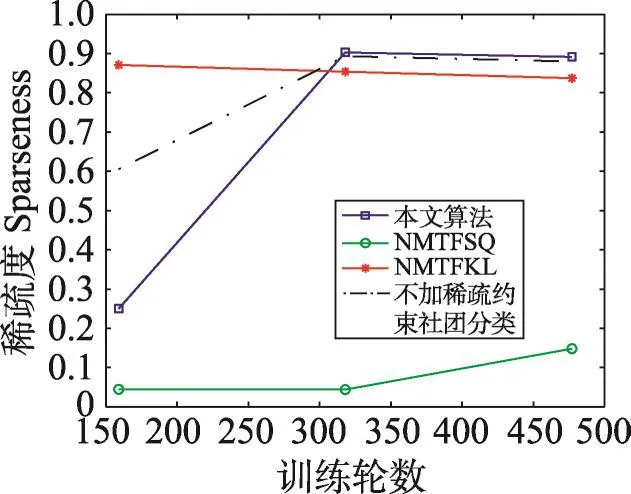
非负矩阵分解是一种常用的矩阵分解方法,它将一个元素非负的矩阵分解为两个非负矩阵的乘积[7-9]。传统NMF问题具体描述为:原始非负矩阵V∈Rm×n,找到两个适当的新的非负矩阵Wm×r和Hr×n,使得V分解成为这两个非负矩阵的乘积,即V≈WH,并且使分解误差尽可能的小。其中W为矩阵的基矩阵,H为系数矩阵。r 自Lee和Seung提出NMF思想(文献[8-9]),非负矩阵分解在科学界广受关注并且不断发展。文献[16]中,Wang等人提出了基于有向和无向图的新的社团发现表达式中的一个点,表示x(i,j)属于第j个社团的权重,Sk×k表示各个社团之间的相互关系。与以往算法分解成两层矩阵不同的是,本算法分为三层,有助于得到社团结构。文献[17]中,Nguyen等人针对文献[18]对于有加权的有向图性能不是很好的缺点,利用KL散度距离作为度量,提出了利用乘性更新(multiplicative update rules)的算法。然而,上述文献都没有考虑矩阵稀疏性的特点。Zhang等人[19]认为,只有非负的约束并不能完全刻画社团结构,他们利用ℓ1范数描述矩阵的稀疏性,并利用坐标下降法(coordinate descent)求解。该算法对有向加权图求解性能较好,针对重叠结构的社团发现也有意义。上述方法虽然都对社团的发现算法进行了详细讨论,但是对于真实的社团发现来讲,除了连接关系,他们没有考虑利用诸如标签、留言等其他的相互关系矩阵来实现社团发现。Tang等人[20]针对社会网络,利用标签等相互关系进行社团结构的划分,并利用交替迭代的方法求解。但是其对于有权重的矩阵来讲性能不是很好。对于现实中的社团结构挖掘来看,这些方法忽视了对社团之间关系的约束,导致算法的性能不是很稳定。 2.3 ℓ1范数与ℓ1/ℓ2范数正则化问题 稀疏是个经典话题,即是用少量重要元素代替大量的数据,使得大多数元素为0而少量元素不为0。由于在高维数据中对于数据的操作是非常费力的,而稀疏性对于解决高维度数据的计算量问题是非常有效的。机器学习中的一个规则化函数ℓ2范数||W||2是应用较广泛的一个优化函数,然而其在实际测试过程中不具有产生稀疏解的能力。而ℓ0范数是指向量中非0的元素的个数,也就是用来找到方程解中具有最小数目的非零项,然而在求解过程中是一个NP问题。因此,引出了ℓ1范数最小化问题,即用ℓ1范数来代替ℓ0与ℓ2范数,以此来找到近似解。 大多数现有的稀疏学习工作是基于ℓ1范数正则化的变种。由于ℓ1范数正则化在应用中方便的凸性、强大的理论保证等,其应用越来越广泛。现今该方法的应用已经促进了线性回归[21]、线性判别分析[22]、偏最小二乘法[13]、逻辑回归[14-15]等模型的稀疏化发展。ℓ1范数正则化得到的目标函数通常描述如下: 其中,X∈Rm×n表示权重矩阵;λ为正则化参数;X中的每一行都是一个特征向量。 近期在机器学习和数学统计领域,稀疏学习工作已经由ℓ1范数正则化延伸到ℓ1/ℓq的正则化[10-12]。当q>1时,ℓ1/ℓq正则化在产生的模型中能够促进组稀疏,因此常常应用到分类和回归问题中。图1展示了该优化问题。 ℓ1/ℓq范数正则化得到的目标函数通常描述如下: Fig.1 Illustration of data matrixA,target matrixY, and weight matrixX图1 数据矩阵A、目标矩阵Y与权重矩阵X关系展示 其中,A为m×n维矩阵;Y=[y1,y2,…,yk]为m×k维矩阵;X=[x1,x2,…,xk]为n×k维矩阵;λ为ℓ1/ℓq正则化系数。 本文研究的是多标记数据分类问题,因此采用的两重稀疏方法是首先利用ℓ1/ℓq范数正则化加入到多标记数据降维中,根据终止-规范化-正则化的步骤,对高维的多标记数据集进行降维,通过正则化,稀疏的矩阵能够显著提高多标记分类的效率。其次将ℓ1范数正则化应用到多标记社团分类中。在文献[16]提到的NMF三层分解结构中,通过向其中加入正则化稀疏项λ,并制定矩阵的更新规则,使得多标记关系在进行社团结构划分时能够取得更显著的社团效果及稀疏度,这有助于理解多标记社团结构的含义。该类优化问题首先得到通过稀疏降维后的数据,再次得到多标记所属社团的稀疏矩阵结构,排除相关性不强的标记干扰,使得每个社团保留最有用的标记信息。目标是将多标记数据充分稀疏,在目标函数上增加稀疏约束条件,使分解后得到的基矩阵W尽可能的稀疏,从而更加节省存储空间,结构更加清晰,标记相关性更能够充分展示。 以下主要介绍在多标记数据集中两重稀疏约束方法作用的不同范围与步骤,包括基于ℓ1/ℓ2范数稀疏性约束的多标记数据降维与基于ℓ1范数稀疏性约束的多标记社团分类。 3.1 基于ℓ1/ℓ2范数稀疏性约束的多标记降维 定义1设多标记数据集为: 其中,n表示多标记数据集样本维数;x表示样本的特征向量;y表示样本标记向量,且y∈{-1,+1}。根据多标记社团发现算法的研究以及对矩阵分解稀疏性的研究,需要ℓ1/ℓq正则化解决多分类的最小二乘问题。这里令q=2,因此基于ℓ1/ℓ2范数正则化稀疏的多标记数据集优化函数通常描述如下: 其中,A∈Rm×n为原始数据矩阵;Y∈Rm×k为目标标记矩阵。优化的目标就是寻找稀疏的权重矩阵X,从而得到使得A稀疏后的降维数据。详见参考文献[23]。 3.2 本文算法 利用NMF算法的稀疏性能够快速提取网络重要节点所属社团这一特点,本文将稀疏性应用到社团发现工作中。主要对多标记社团划分的工作进行改进,将多标记关系矩阵运用基于ℓ1范数稀疏约束的非负矩阵分解算法,得到多标记的社团分类。基于两重稀疏性约束的多标记社团分类方法步骤如下。 (1)输入:多标记训练数据集特征矩阵A,标记矩阵Y,正则化参数λ,训练轮数T,MAHR训练基分类器C。 (2)输出:多标记所属社团矩阵G。 (4)利用ℓ1/ℓ2范数正则化对多标记数据集A进行降维,得到稀疏后的降维矩阵A*。 (5)利用MAHR算法,对A*进行相应的训练,得到综合模型Z,标记关系矩阵所需权重β与α。 (6)根据Z、β与α,得出多标记间评分矩阵S,其中根据评分得到关系矩阵规范化并重组,得到多标记关系矩阵V。 (7)根据NMF规则,将矩阵V分解为三层结构,即V≈XSXT。 更新X:xi+1=xi+Δx。其中Δx为添加稀疏正则化项的稀疏基矩阵增量。 更新S:si+1=si+Δs。其中Δs为社团关系矩阵增量。 (8)从矩阵X中找到每个标记的最大值与所属社团标号,得到多标记节点所属社团C。 其中k代表社团数量,根据算法中系数矩阵X来找到多标记所属的社团分类。矩阵X表示一个二维的数量为k的社团,行对应标记节点类别,列对应社团类别,矩阵X的每一行最大的元素所对应的列则可标识为对应标记所在的社团类别。 基于两重稀疏性约束的多标记社团分类方法就是在原目标函数上增加约束条件来获取尽可能稀疏的标记所属社团的分类信息。鉴于当前工作中基于ℓ1/ℓ2范数稀疏约束的数据降维方法应用较广,本文将工作重点放在多标记社团分类过程中。在前面的基础上考虑对非负向量X加ℓ1范数约束条件,即最小化转换为矩阵的形式就是为了使矩阵X充分稀疏,最小化矩阵X中所有元素的和。 因此,加稀疏的多标记社团划分为三层模式,V≈XSXT。V的转置形式VT≈(XSXT)T=XSTXT。 其中,V表示有向加权图的邻接矩阵;S描述社区之间的权值关系;X描述节点属于某个社区的权值,并且X中元素值在[0,1]之间。表示Frobenius范数代表能够使得x中的元素更好地属于某一社团的ℓ1范数模型,用来控制模型的稀疏度,让节点尽可能被清晰地划分。也就是说,通过控制矩阵X中每一个多标记元素x(i,j)属于所有社团的稀疏度(使得多标记所属社团的权重尽可能多地为0),用来达到稀疏效果的最优化。优化目标中的λ就能够平衡矩阵X的稀疏性与精确性,使稀疏的结果准确度更高。根据文献[24]的方法,得到该算法的更新规则[25],即: 因此,将L分别对X和S*求导,得: 更新X、S的增量为: 最终得到了稀疏后的标记所属社团关系矩阵。 4.1 实验设置 本实验共使用1个人工数据集和3个真实数据集,人工数据集为Data,是34×34维的0-1对称关系矩阵,真实数据集包括邮件分析数据集Enron[26]、文献管理数据集BibTex[27]和生物领域的基因数据集Genbase[28],表1给出了这些数据集的统计信息。通过基于两重稀疏性约束的多标记社团分类方法,首先得到降维后的多标记特征矩阵,再次根据MAHR算法得到多标记的评分矩阵,进而应用ℓ1范数约束得到多标记社团关系,并对多标记所属社团矩阵进行解释。 Table 1 Experimental datasets表1 实验数据集 实验环境操作系统为Windows7,工具软件为Matlab R2013a。 4.2 结果分析 本节列举出根据加稀疏约束的多标记社团分类算法得到的标记所属矩阵关系,并在4个数据集上进行实验效果验证。根据数据集的维数、标记数量等特点,将上述几个数据集划分为个数不同的社团,并且通过本文算法得到标记所属社团矩阵。矩阵分解后的系数矩阵能反映分解的效果,因此对分解后的系数矩阵X及算法的一些指标进行分析,并比较多标记关系,获取所需的训练轮数与各项指标的关系。其中“↑”表示越大越好,“↓”代表越小越好,“·”表示在对应指标比较上,本文算法优于比较方法。 根据文献[29]提出的稀疏度度量公式对分解后的基矩阵和系数矩阵进行度量,公式如下: 其中,n代表向量X的维度;m表示向量X的元素个数;xi代表向量X第i个元素的值。Sparseness(x)的值在[0,1]之间,并且值越接近1表示向量的稀疏度越高。本文对比的是X中所有列向量的稀疏度取平均值。 矩阵X的模块度是目前常用的一种衡量网络社区结构强度的方法[30-31],值越接近1表示网络划分的社团结构强度越好。公式为: 其中,m为网络中边的总数;i、j分别为网络中的节点;Vij表示i、j的邻接关系;N为节点集合;ki为点i的度;Ci和Cj分别表示点i、j所在的两个社区。 分解误差表示矩阵分解后与原矩阵的误差,根据文献[32]用Frobenius范数衡量,误差值越小表示分离效果越好。公式为: 分解时间表示几个算法在对多标记关系矩阵处理并进行矩阵分解过程中所需要的时间,时间越短表示算法处理速度越快。 4.2.1 性能比较 表2~表5分别统计了表1中几个数据集的实验结果。具体内容如下:将Data划分为5个社团,Genbase的多标记关系划分为3个社团,Enron数据集的多标记关系划分为2个社团,BibTex划分为22个社团。参加比较的算法有应用ℓ2范数正则化的NMTFSQ[19]社团发现算法,应用KL距离(Kullback-Leibler divergence)的NMTFKL[19]社团发现算法以及不加任何稀疏约束的基于NMF的社团发现算法。 表2展示了人工数据集Data上的实验结果。其中令本文算法中ℓ1范数的正则化项λ=1.5,划分的社团个数k=5。由于Data数据集已经是元素间的关系矩阵,那么对于基于ℓ1/ℓq范数稀疏性约束的多标记数据降维步骤省略,直接进入社团发现过程。 Table 2 Average performance for this paper method and compared methods in Data表2 Data数据集中本文算法与比较算法的平均性能 从表2中可以看出,本文算法在模块度、分解误差、稀疏度3个指标上取得了比其他社团发现方法更优的效果。而在分解时间方面,NMTFSQ所用时间最长,而本文算法与其他算法的结果相差不大。 表3统计了上述几个数据集上的实验结果,展示了数据集Genbase在λ=1.5,社团个数k=3,多标记关系训练轮数为4倍的样本标记维数(rounds=108)情况下,本文算法同已有的多种非负矩阵算法的比较结果。 从表3中可以看出,本文算法同样在模块度、分解误差、稀疏度3个指标上取得了比其他社团发现方法更优的效果。而在分解时间方面,NMTFSQ所用时间最长,而本文算法与其他算法的结果相差不大。 Table 3 Average performance for this paper method and compared methods in Genbase表3 Genbase数据集中本文算法与比较算法的平均性能 表4统计了上述几个数据集上的实验结果,展示了数据集Enron在λ=1.5,社团个数k=2,多标记关系训练轮数为3倍的样本标记维数(rounds=212)情况下,本文算法同已有的多种非负矩阵算法的比较结果。 Table 4 Average performance for this paper method and compared methods in Enron表4 Enron数据集中本文算法与比较算法的平均性能 从表4中可以看出,本文算法在Enron数据集上不是很理想,仅在模块度和分解误差两个指标上表现良好。 表5统计了上述几个数据集上的实验结果,展示了数据集Bibtex在λ=1.5,社团个数k=22,多标记关系训练轮数为3倍的样本标记维数(rounds=477)情况下,本文算法同已有的多种非负矩阵算法的比较结果。 根据表5的结果不难看出,本文算法在除了分解时间指标以外的其余3个最有意义的指标上取得最好的效果,且优势比较明显。 因此,在4个常用的不同领域的数据集中,每个数据集在相同的实验环境及参数设置条件下,同已有的非负矩阵分解算法相比,本文算法在模块度、稀疏度方面达到了最优,而在分解时间与误差值方面,同最优算法相比,均相差不大,根据模块度最大选择多标记社团分解算法才具有更高的准确率。同时,稀疏度越高表明得到的多标记所属社团分类更明确。因为未加稀疏的公式简便,所以从时间效果分析,未加稀疏的多标记社团发现算法时间最短,而本文算法相对于NMTFSQ和NMTFKL算法来说,在处理时间上显著缩短。 Table 5 Average performance for this paper method and compared methods in BibTex表5 BibTex数据集中本文算法与比较算法的平均性能 4.2.2 基于ℓ1/ℓ2范数稀疏约束的影响 由于本文是基于两重稀疏约束的算法,那么在第一层稀疏即数据加入ℓ1/ℓ2范数约束对标记关系的影响需要验证。图2~图7分别统计了表1中几个数据集在不经过稀疏降维的情况下与基于ℓ1/ℓ2范数稀疏约束的情况下模块度与稀疏度的对比结果,目的是为了验证稀疏降维有无保留最重要的属性以及对多标记关系的影响。设3个数据集在降维过程中的ℓ1/ℓ2范数正则化项λ12=0.02。 图2~图4表示对于数据集Genbase、Enron、Bib-Tex,基于ℓ1/ℓ2范数稀疏约束进行多标记数据降维后与原特征数据在模块度Q上的效果对比。图5~图7表示对于数据集Genbase、Enron、BibTex,基于ℓ1/ℓ2范数稀疏约束进行多标记数据降维后与原特征数据在稀疏度Sparseness上的效果对比。比较算法包含本文算法及其他3种算法。 对于图2~图4,从模块度方面讲,原多标记的高维数据经过ℓ1/ℓ2范数稀疏降维后再进行社团划分的方法,4个算法在数据集Genbase和BibTex上取得了比较好的效果,将不必要的属性稀疏降维后,模块度不仅没有降低反而有所提高,说明降维之后剩余的特征属性具有更明显的特征,对多标记数据训练过程中得到的相关性更有帮助,从而能够更加明显地展示出多标记的社团结构。而在Enron数据集上的表现并不令人满意,模块度成为负值,说明该数据集在稀疏降维后得到的标记关系失去了社团的性质。 对于图5~图7,同样可以看出ℓ1/ℓ2范数稀疏降维对稀疏度的影响。在数据集BibTex的结果中,除了在NMTFKL算法上稀疏度稍微减小以外,在其他算法上都有所提高,或者是提高幅度不明显;在数据集Enron中,效果差强人意,稀疏度减小幅度并不大;在数据集Genbase中,本文算法和NMTFKL算法的稀疏度有所减小,而其余两个增大。 Fig.4 Comparison ofQwhether usingℓ1/ℓ2-norm in BibTex图4 BibTex中有无ℓ1/ℓ2范数模块度比较 Fig.5 Comparison of sparseness whether usingℓ1/ℓ2-norm in Genbase图5 Genbase中有无ℓ1/ℓ2范数稀疏度比较 Fig.6 Comparison of sparseness whether usingℓ1/ℓ2-norm in Enron图6 Enron中有无ℓ1/ℓ2范数稀疏度比较 Fig.7 Comparison of sparseness whether usingℓ1/ℓ2-norm in BibTex图7 BibTex中有无ℓ1/ℓ2范数稀疏度比较 总体来看,在3个数据集进行基于ℓ1/ℓ2范数稀疏约束后,在个别数据集的个别算法指标上有减弱的效果,但是整体来说趋于稳定,甚至模块度、稀疏度都有增强,社团结构更加明显。由此说明,在多标记数据集降维后,不仅没有影响重要特征,反而保留了重要的特征,并能够对标记关系的训练产生影响,从而明确社团结构。标记社团的结果同完全由原始数据训练得到的标记关系差别不大,同时预处理的训练时间因为稀疏的作用而大幅度减少,更加简便快捷,加入ℓ1/ℓ2范数降维后的数据处理更为优越。 4.2.3 标记关系训练轮数的影响 在MAHR算法过程中,标记关系是由算法训练迭代得到,表示了标记的相互作用程度大小,因此可以用来量化标记关系。图8~图13给出了数据集Genbase、Enron和BibTex在λ=1.5,社团个数分别为k=3,k=2,k=22时,模块度Q和稀疏度Sparseness同多标记社团关系的训练轮数的关系。 由图8~图13可以得出,本文算法在3个数据集中的模块度基本处于最高的状态,且变化较为稳定。无论是在模块度还是稀疏度方面,本文基于ℓ1稀疏约束的社团发现算法要比不加稀疏约束的普通社团发现算法表现好。虽然在稀疏度方面4个算法表现有好有坏,但是可以明确的是,随着多标记社团关系训练轮数的增加,几个算法的模块度和稀疏度整体来说呈增加的趋势。这样的结果说明,训练轮数增加,得到的多标记间的相关联系就越紧密,关系矩阵更加突出,更有助于稀疏,有助于多标记社团关系基于稀疏进行分解。 Fig.8 Training rounds toQin Genbase图8 Genbase中轮数对模块度的影响 Fig.9 Training rounds toQin Enron图9 Enron中轮数对模块度的影响 Fig.10 Training rounds toQin BibTex图10 BibTex中轮数对模块度的影响 Fig.11 Training rounds to sparseness in Genbase图11 Genbase中轮数对稀疏度的影响 Fig.12 Training rounds to sparseness in Enron图12 Enron中轮数对稀疏度的影响 Fig.13 Training rounds to sparseness in BibTex图13 BibTex中轮数对稀疏度的影响 同时,列举了数据集BibTex在不同的训练轮数下,在相同的社团划分个数k=22时,随着正则化项λ的改变,稀疏度的变化情况,如图14所示。 Fig.14 Relationship between λand sparseness图14 正则化项λ与稀疏度的关系 根据图14,探索了在不同的训练轮数下,基于稀疏约束的正则化项λ取值同稀疏度的关系。由结果可以看出,在训练轮数为159次时,λ在取值为5.0左右稀疏度达到最大值0.966 6,随后呈现递减趋势;在训练轮数为318次时,λ在取值为10.0左右稀疏度达到最大值0.955 7,随后呈现下降趋势;在训练轮数为477次时,λ在取值为15.0左右稀疏度达到最大值0.942 9,随后呈现下降趋势。由此可以看出,随着λ的增大以及训练轮数的改变,稀疏度的大小是变化的,总体呈现先增后减的趋势。也就是说,稀疏度同增加的稀疏约束项息息相关,正则化项λ的变化影响到最后的稀疏程度,需要不断测试找到一个合适的λ来达到需要的稀疏效果,但是要注意过拟合的发生。 由上述实验结果发现,在选取相同的实验条件下,从矩阵结构来看,基于两重稀疏表示的多标记社团分类方法结构更加清晰且运算简便。经过多个性能指标的对比发现,基于稀疏约束的多标记社团分类算法得到了更好的稀疏性、实用性与可解释性,在多项指标上有良好的效果。 针对已有的多标记社团发现样本数目多,标记不单一且标记特征具有冗余的现状,本文提出了基于两重稀疏约束的多标记社团分类方法,针对多标记特征数据训练繁琐以及社团发现未考虑稀疏约束的问题,通过为多标记分类过程及矩阵分解过程中的原目标函数添加稀疏正则化项,从而达到将多标记关系矩阵稀疏的效果。与已有的多标记社团发现算法进行比较,本文算法不仅运算简便,提高了训练效率,同时也有效提高了数据分解后的稀疏度,增强了数据表达的可解释性,保留了原始样本中最重要的节点。实验结果证明,本文算法是有效的,在保证最重要信息的基础上,对处理大规模多标记数据有着较好的分类效果。 [1]Lu Jianjiang,Zhang Yafei,Xu Weiguang,et al.Intelligentretrieval technology[M].Beijing:Science Press,2009. [2]Klimt B,Yang Yiming.Introducing the Enron corpus[C]//Proceedings of the 1st Conference on Email and Anti-Spam, Mountain View,USA,Jul 30-31,2004.Menlo Park,USA: AAAI,2004. [3]Duan Fei,Zhang Yujin.A new algorithm for maximum dictionary learning for sparse representation[J].Journal of Tsinghua University:Natural Science Edition,2012,52(4):566-570. [4]Wang Xiaofan,Liu Yabing.A survey of community structure in complex networks[J].Journal of University of Electronic Science and Technology of China,2009,38(5):537-543. [5]Wang Xiaofan.Complex network theory and its application [M].Beijing:Tsinghua University Press,2006. [6]Huang Shengjun,Yu Yang,Zhou Zhihua.Multi-label hypothesis reuse[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Beijing,Aug 12-16,2012.New York:ACM,2012: 525-533. [7]Huang Gangshi,Zhang Yafei,Lu Jianjiang,et al.A constrained non negative matrix factorization method[J].Journal of Southeast University:Natural Science Edition,2004,34(2):189-193. [8]Lee D D,Seung H S.Learning the parts of objects by nonnegative matrix factorization[J].Nature,1999,401(6755): 788-791. [9]Lee D D.Algorithms for non-negative matrix factorization [J].Advances in Neural Information Processing Systems, 2001,13(6):556-562. [10]Argyriou A,Evgeniou T,Pontil M.Convex multi-task feature learning[J].Machine Learning,2008,73(3):243-272. [11]Bach F R.Consistency of the group lasso and multiple kernel learning[J].Journal of Machine Learning Research,2007,9 (2):1179-1225. [12]Berg E V D,Schmidt M,Friedlander M P,et al.Group sparsity via linear-time projection[R].UBC,2008. [13]Lê Cao K A,Rossouw D,Robert-Granié C,et al.A sparse PLS for variable selection when integrating omics data[J]. Statistical Applications in Genetics&Molecular Biology, 2008,7(1):35. [14]Koh K,Kim S J,Boyd S.An interior-point method for large-scale L1-regularized logistic regression[J].Journal of Machine Learning Research,2007,8(3):1519-1555. [15]Liu Jun,Chen Jianhui,Ye Jieping.Large-scale sparse logistic regression[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Paris,Jun 28-Jul 1,2009.New York:ACM,2009: 547-556. [16]Wang Fei,Li Tao,Wang Xin,et al.Community discovery using nonnegative matrix factorization[J].Data Mining& Knowledge Discovery,2011,22(3):493-521. [17]Nguyen N P,Frank C,Moltz C C,et al.Aspiration rate following chemoradiation for head and neck cancer:an underreported occurrence[J].Radiotherapy and Oncology,2006, 80(3):302-306. [18]Brunet J P,Tamayo P,Golub T R.et al.Metagenes and molecular pattern discovery using matrix factorization[J].Proceedings of the National Academy of Sciences,2004,101 (12):4164-4169. [19]Zhang Yu,Yeung D Y.Overlapping community detection via bounded nonnegative matrix tri-factorization[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Beijing, Aug 12-16,2012.New York:ACM,2012:606-614. [20]Tang Jiliang,Liu Huan.Unsupervised feature selection for linked social media data[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Beijing,Aug 12-16,2012.New York: ACM,2012:904-912. [21]Tibshirani R.Regression shrinkage and selection via the Lasso [J].Journal of the Royal Statistical Society:Series B Methodological,1996,58(1):267-288. [22]Ye Jieping,Chen Jianhui,Janardan R,et al.Developmental stage annotation of drosophila gene expression pattern images via an entire solution path for LDA[J].ACM Transactions on Knowledge Discovery from Data,2008,2(1):1-21. [23]Golub T R,Slonim D K,Tamayo P,et al.Molecular classification of cancer:class discovery and class prediction by gene expression monitoring[J].Science,1999,286(5439):531-537. [24]Wang Dingding,Li Tao,Zhu Shenghuo,et al.Multi-document summarization via sentence-level semantic analysis and symmetric matrix factorization[C]//Proceedings of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval,Singapore,Jul 20-24,2008.New York:ACM,2008:307-314. [25]Zhang Liangliang,Pan Zhisong,Li Guopeng,et al.Weighteddirected community detection method based on Wavelet denoising[J].Journal of Data Acquisition and Processing, 2014,29(5):833-839. [26]Klimt B,Yang Yiming.The Enron corpus:a new dataset for Email classification research[C]//LNCS 3201:Proceedings of the 15th European Conference on Machine Learning,Pisa, Sep 20-24,2004.Berlin,Heidelberg:Springer,2014:217-226. [27]Katakis I,Tsoumakas G,Vlahavas I.Multilabel text classification for automated tag suggestion[C]//Proceedings of the ECML/PKDD 2008 Workshop on Discovery Challenge,Antwerp,Belgium,Sep 15-19,2008. [28]Diplaris S,Tsoumakas G,Mitkas PA,et al.Protein classification with multiple algorithms[C]//LNCS 3746:Proceedings of the 10th Panhellenic Conference on Informatics,Volas, Greece,Nov 11-13,2005.Berlin,Heidelberg:Springer,2005: 448-456. [29]Zhang Wei,Liu Ju,Sun Jiande,et al.A new two-stage approach to underdetermined blind source separation using sparse representation[C]//Proceedings of the 2007 International Conference on Acoustics,Speech and Signal Processing, Honolulu,USA,Apr 16-20,2007.Piscataway,USA:IEEE, 2007:953-956. [30]Newman M E.Fast algorithm for detecting community structure in networks[J].Physical Review E,2004,69(6):279-307. [31]Guillaume J L,Lambiotte R.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics Theory &Experiment,2008,30(2):155-168. [32]Liao Feng,Gao Xingbao,Yang Xuan.An improved non negative matrix factorization algorithm[J].Journal of University of Jinan:Natural Science Edition,2008,22(2):193-196. 附中文参考文献: [1]陆建江,张亚非,徐伟光,等.智能检索技术[M].北京:科学出版社,2009. [3]段菲,章毓晋.一种面向稀疏表示的最大问隔字典学习算法[J].清华大学学报:自然科学版,2012,52(4):566-570. [4]汪小帆,刘亚冰.复杂网络中的社团结构算法综述[J].电子科技大学学报,2009,38(5):537-543. [5]汪小帆.复杂网络理论及其应用[M].北京:清华大学出版社,2006. [7]黄钢石,张亚非,陆建江,等.一种受限非负矩阵分解方法[J].东南大学学报:自然科学版,2004,34(2):189-193. [25]张梁梁,潘志松,李国鹏,等.基于小波去噪的有向加权社团发现研究[J].数据采集与处理,2014,29(5):833-839. [32]廖锋,高兴宝,杨轩.一种改进的非负矩阵分解算法[J].济南大学学报:自然科学版,2008,22(2):193-196. LI Na was born in 1990.She is an M.S.candidate at College of Command Information Systems,PLA University of Science and Technology.Her research interests include pattern recognition and machine learning,etc. 李娜(1990—),女,河北保定人,解放军理工大学指挥信息系统学院硕士研究生,主要研究领域为模式识别,机器学习等。 潘志松(1973—),男,江苏南京人,2002年于解放军理工大学指挥信息系统学院获得博士学位,现为解放军理工大学教授、博士生导师,CCF会员,主要研究领域为模式识别,机器学习等。 REN Yiqiang was born in 1987.He is an engineer at SIEMENS Power Automation Co.,Ltd..His research interests include relay protection of power systems,supervisory control and data acquisition system,etc. 任义强(1987—),男,河北保定人,西门子电力自动化有限公司工程师,主要研究领域为电力继电保护,监控与数据采集系统等。 LI Guopeng was born in 1983.He is a Ph.D.candidate at College of Command Information Systems,PLA University of Science and Technology.His research interests include pattern recognition and machine learning,etc. 李国朋(1983—),男,陕西兴平人,解放军理工大学指挥信息系统学院博士研究生,主要研究领域为模式识别,机器学习等。JIANG Mingchu was born in 1989.He is an M.S.candidate at College of Command Information Systems,PLA University of Science and Technology.His research interests include pattern recognition and machine learning,etc.蒋铭初(1989—),男,江苏淮安人,解放军理工大学指挥信息系统学院硕士研究生,主要研究领域为模式识别,机器学习等。 Multi-Label Community Classification Method Based on Double Sparse Representation* LI Na1,2,PAN Zhisong1+,REN Yiqiang3,LI Guopeng1,4,JIANG Mingchu1 In multi-label learning,the correlation between labels has been more and more widely used,and it is necessary to show the relationship between them.Compared with previous studies,training process is extremely complicated and time-consuming due to the high dimensionality feature of multi-label data,so sparse optimization becomes essential;meanwhile,the relationship among labels has not been thoroughly excavated,so how to learn multi-label classification and study the correlation between all markers more effectively and conveniently becomes a necessity. This paper presents a method constraint on double sparse representation in multi-label classification,which first usesℓ1/ℓ2-norm regularization to sparse multi-label data to convenient for following researches,and then appliesℓ1-norm into community detection to effectively detect communities.By this it shows the deep meaning of label relationship.Experiments show that this method can rapidly and accurately study and train multiple labels,and accurately display label connection at the same time. multi-label;label relation;non-negative matrix factorization(NMF);ℓ1/ℓ2-norm;ℓ1-norm ng was born in 1973.He the Ph.D.degree from PLA University of Science and Technology in 2002.Now he is a professor and Ph.D.supervisor at PLA University of Science and Technology,and the member of CCF.His research interests include pattern recognition and machine learning,etc. A TP391 *The National Natural Science Foundation of China under Grant No.61473149(国家自然科学基金). Received 2016-02,Accepted 2016-04. CNKI网络优先出版:2016-04-18,http://www.cnki.net/kcms/detail/11.5602.TP.20160418.1031.002.html


3 基于两重稀疏约束的多标记社团分类方法




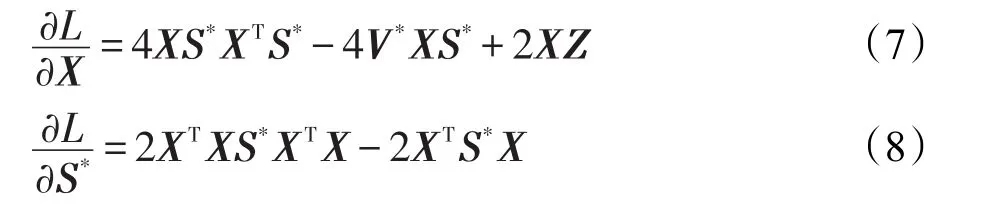
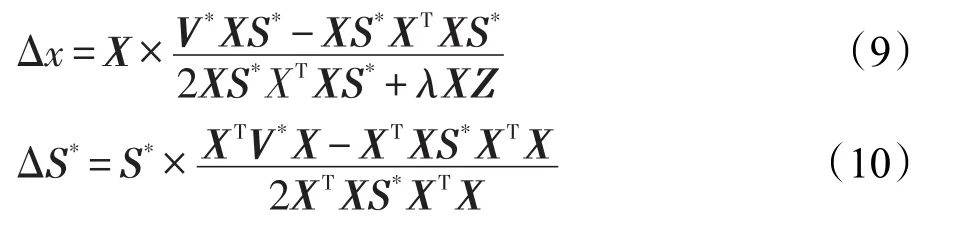
4 实验分析

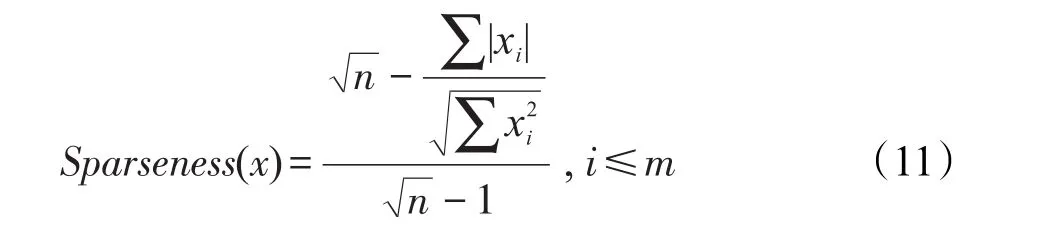
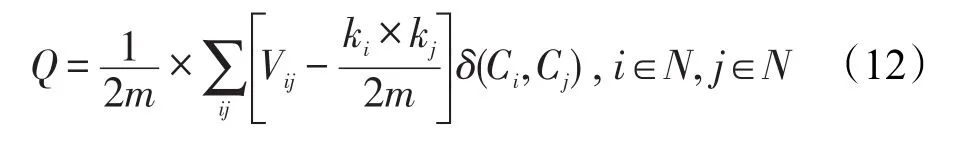







5 结束语





1.College of Command Information Systems,PLAUniversity of Science and Technology,Nanjing 210007,China
2.The 32nd Research Institute of China Electronic Technology Group Corporation,Shanghai 201808,China
3.SIEMENS PowerAutomation Co.,Ltd.,Nanjing 211100,China
4.XiƳan Communications Institute,XiƳan 710106,China
+Corresponding author:E-mail:panzs@nuaa.edu.cn
