指纹三角区域特征点融合匹配STSF算法研究*
2017-06-15张志忠
艾 乐,张志忠
1.中国人民公安大学 刑事科学技术学院,北京 100038
2.中国科学院 自动化研究所 复杂系统管理与控制国家重点实验室,北京 100190
指纹三角区域特征点融合匹配STSF算法研究*
艾 乐1+,张志忠2
1.中国人民公安大学 刑事科学技术学院,北京 100038
2.中国科学院 自动化研究所 复杂系统管理与控制国家重点实验室,北京 100190
AI Le,ZHANG Zhizhong.Study of feature fusion matching STSF algorithm for partial delta fingerprint. Journal of Frontiers of Computer Science and Technology,2017,11(6):950-958.
目前大部分指纹自动识别系统(automatic fingerprint identification systems,AFIS)所采用的特征点匹配算法需以准确提取特征点为前提,这些算法在面对存在高度畸变且残缺不全的现场指纹时,往往难以准确识别指纹图像。在相似三角形匹配算法的基础上,研究了SIFT(scale invariant feature transform)特征点与二级特征点之间的位置关系,克服了相似三角形之间尺度不一的问题。此外,提出了一种基于贝叶斯统计推断的相似三角形与SIFT融合算法(similar triangle SIFT feature,STSF)。实验结果表明,STSF算法能够有效提升残缺指纹匹配的精度和计算效率。
指纹匹配;特征融合;残缺指纹
1 引言
指纹由于其人各不同、终身基本不变的性质,被广泛用于法庭科学领域及商用、民用人身识别领域。指纹自动识别系统(automatic fingerprint identification systems,AFIS)的应用为指纹的储存、识别、快速检索和比对提供了巨大帮助。AFIS中的核心指纹匹配算法大致可分为基于相关性、基于特征点位置关系或无特征点算法3种。相关性匹配算法(correlationbased matching)[1-2]即将两枚指纹图像叠加并计算位移和扭转角度。基于特征点匹配算法是分别提取两幅指纹图片中的特征点,从而进行特征点查询。无特征点匹配算法(non-minutiae feature based matching)[3-4]使用的是纹线流向、类型等非二级特征。目前大部分AFIS系统采用的是特征点匹配算法,这是由于其更符合指纹学界对指纹鉴定所用二级特征的理解。此类算法都需要以准确提取特征点为前提,面对现场指纹时,需要克服以下几个问题:(1)即使是同一个手指,每次遗留指纹时由于受力的方向、大小、作用方式、承痕客体表面情况、附着物等多种条件影响,很难形成完全一样的两枚指纹,相同特征点也必然会存在不同程度的位移、形变等。因此基于特征点的匹配算法需要具备抗畸变能力。(2)现场指纹多为局部指纹,二级特征点数量有限,如何仅依靠有限的特征点,在千万级数据库中检索出同源指纹,并使其排序靠前。
有人为此提出了特征点组匹配算法[5],用于说明特征点的几何位置关系,其缺点是需要预估指纹变形程度。在此基础上,有学者提出了相似三角形方法(similar vector triangle matching algorithm)[6],不必依赖指纹中心点及三角点,且具有一定的抗位移和形变的能力,但仍需准确提取特征点和相当多的特征点数目。Bazen等人[7]提出了一种优先于整体定位的方法,将某一特征点及其邻近的两个特征点形成一个组合关系,以此为基准在档案指纹中寻找相似的组合结构。虽然特征组中可能存在伪特征,但统计所有特征点集后计算最小方差,即可消除误差得到最优结果,基于特征点组的定位方法还可用于变形指纹,消除系统算法中的误识率(false acceptance rate)。随后又有人提出了完全独立于整体特征定位的局部特征点定位方法,所利用的均为局部特征点组合关系[8-9]。Abraham等人[10]提出了一种形状及方向混合描述符(hybrid shape and orientation descriptor),可以有效过滤可疑特征组,同时利用纹线方向提高匹配得分。此种方法尤其适用于缺少中心点或三角点的残缺指纹。
SIFT(scale invariant feature transform)特征点作为通用图像匹配算法的基础,反映了图像的局部灰度结构,具有很好的尺度、平移和旋转不变性,即使在指纹图片存在放大或缩小、扭曲、位移时,也可保持稳定,且SIFT特征点数目众多,因此可用于残缺指纹的特征点提取工作。但SIFT特征也存在缺点:易受指纹图片背景影响,难以处理指纹图像的畸变问题,会形成伪特征,错误率也随之提高。因此有人提出将几种特征点提取方法综合运用以减低错误率,提高匹配度的方法。如Malathi等人[11]提出将提取的汗孔特征和SIFT特征匹配得分进行加权,可以大大提升残缺指纹比对的准确率,但是当图像尺寸降低时,匹配精度降低。
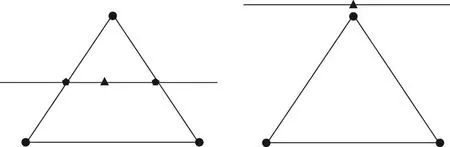
三角特征模式匹配作为特征点匹配的主流算法,具有不错的抗畸变能力[12],但对于残缺指纹,能利用的特征点数目较少,往往匹配上具有相似比例但大小不同的三角特征,如图1所示。另一方面,SIFT特征点具有旋转、平移和尺度不变性,且数目众多,但会出现计算复杂度高,伪特征点多等问题,直接进行SIFT特征点匹配错误率高。因此本文旨在将二者结合起来,设计更好的匹配算法。犯罪现场能够提取到的多是犯罪分子抓取、握取物品遗留的手指侧面指纹,其中三角区域二级特征点出现频率较高,三角点易辨识。因此本文针对指纹三角区域开展研究,提升特征点匹配的准确性,减少AFIS检索时间,提高工作效率。

Fig.1 Matching vector triangle of two different fingerprints with different scales图1 两枚异源指纹匹配的尺度不一三角特征
2 算法与模型
2.1 相似三角形匹配算法
假设现场指纹上二级特征点数量为P={P1,P2,…,Pn},档案指纹上二级特征点数量为Q={Q1,Q2,…,Qn},每个特征点都有对应的横纵坐标、方向x、y、θ。设Pi和Qi分别表示来自现场指纹和档案指纹上的某一点。对每一个由任意3个P点组成的三角形,依据以下条件寻找档案指纹中的相似三角形。
(1)将三角形3条边按长短由低到高排列(Lp1,Lp2,Lp3)(Lq1,Lq2,Lq3),根据边长,调整3个节点的顺序(Ap,Bp,Cp)(Aq,Bq,Cq)。
(2)计算3条边的形变程度:

(3)计算角度差:


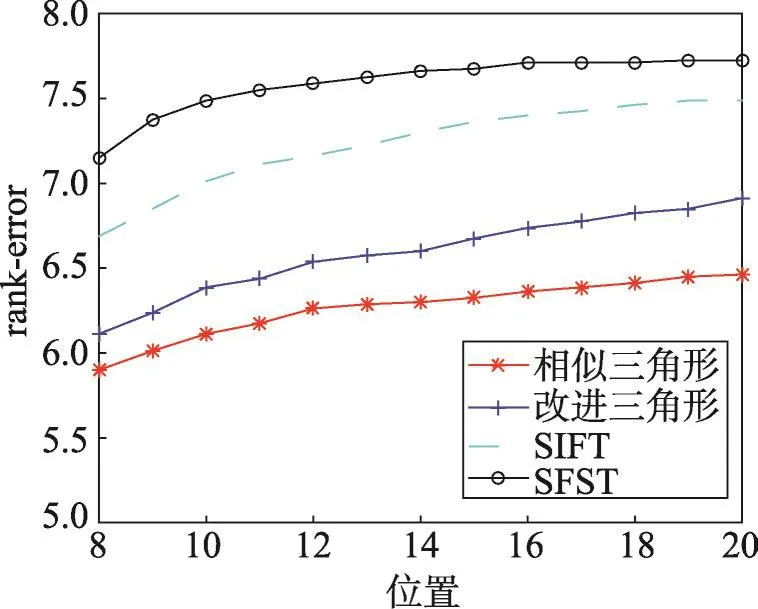
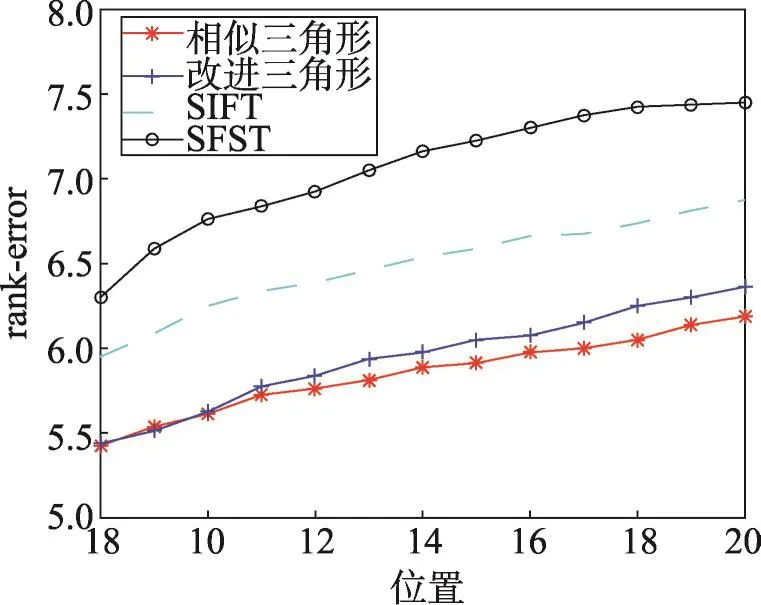
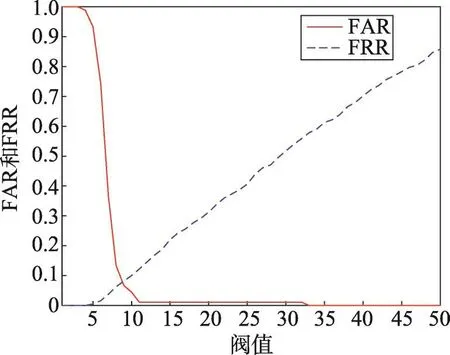
设T1为边长形变的阈值,T2为角度形变的阈值,若满足 ||K1-K2 旋转角度为: 每个特征点的横纵坐标即可进行霍夫变换: 计算得到匹配后的特征点坐标x′、y′、θ′,当欧式距离小于某一阈值时,认为两个特征点匹配。根据两幅图像匹配的特征点个数计算得分,在实验中采用了常见的但实验效果不如直接采用特征点个数作为匹配得分,这是因为残缺指纹特征点数目较少,匹配点个数能够更好反应二者的匹配程度。 上述方法虽然能够很好地解决特征点三角形形状相似的问题,但是难以解决相似三角形尺度不一的问题。由于指纹图像的畸变问题,如果设置一个比较紧的形变阈值,会丢失很多正确的匹配三角形对,同时设置比较大的形变阈值会浪费大量的计算资源。 文献[13]提出的欧氏距离矩阵分析(Euclidean distance matrix analysis,EDMA)方法认为,从两个不同的图形中寻找地标点需要借助相对的位置关系,能够有效地克服旋转、尺度等问题。大量的指纹图像检索方法[14]也都依据特征点位置关系进行建模,达到快速精准匹配的目的,然而残缺指纹匹配中难以寻找大量的二级特征点,因此本文希望通过SIFT特征点与二级特征点之间的位置关系进行建模,解决匹配三角形对中出现的大量的尺度不一的情形。计算二级特征点三角形内SIFT数目Nij,计算方法可由简单的射线法完成,如图2所示。如果二级特征点三角形内的SIFT数目相差较多,则可直接过滤三角形对。实验结果表明,不仅在精度上还是在时间效率上算法性能都有所提升。 Fig.2 Ray methods for calculating the number of SIFT图2 射线法SIFT数目计算方法 2.2 SIFT特征点匹配算法 SIFT算法一般采用128维的统计直方图作为描述符。指纹图像由于脊线纵横,灰度边缘信息丰富,特征点数目往往有上千个,两幅指纹图像的SIFT特征点的匹配,需要耗费大量时间,剔除错误匹配点时间消耗也会大大增加,对于大规模指纹匹配算法并不适用。但是残缺指纹由于受采集场景的条件限制,获取的特征点数目有限,SIFT算子需要更强的鲁棒性,才能满足匹配需求。另一方面,残缺指纹图像所需的纹理特征都是基于脊线走势、变化的微小细节特征,因此只选取尺度和极值在适当范围内的SIFT算子作为有效特征点。本文基于欧式度量进行相似性匹配,运用树结构进行搜索匹配,使用Ransac算法对SIFT特征点进行筛选,剔除不匹配特征点。SIFT特征点匹配得分按照下列方法计算: 2.3 STSF融合算法 SIFT特征点反应了指纹图像的脊线纹理区别,而二级特征点相似三角形匹配算法与指纹专家鉴定方法类似,依照二级特征点之间的几何位置关系确定指纹图像关系。从两种匹配方式中提取互补信息,能够有效提升残缺指纹的匹配准确性。本文运用贝叶斯统计的方法来获取二者的互补信息[15]。 设指纹图像i与指纹图像j的两种匹配得分为scoreSIFT、scoretriangle,则指纹图像i与指纹图像j在当前的匹配分数下,匹配的概率为: 其中,G表示指纹图像i与指纹图像j真正匹配;I表示指纹图像i与指纹图像j不匹配。该后验概率表明在不同特征空间下的得分置信度。因此最终的得分为: weight为权重函数,定义为: 直观来说,p(G|score)越高,当前得分下真正匹配的概率越高,当前特征空间的得分权重应该提高;反之p(G|score)越低,则说明二者并不是真正的匹配,当前特征空间的得分权重应该降低。 p(G|score)的概率估计有多种方式,可以在模型中加入先验知识,但为了便于分析,取p(G)=p(I)。本文采用基于统计直方图的经验估计,定义为: 其中,NG(score)为训练集中当前得分下直方图箱宽区间内正确匹配的个数;NI(score)为训练集当前得分下直方图箱宽区间内错误匹配的个数。 为了验证特征点融合匹配算法的有效性,本文选取公开数据集FVC2002指纹库进行实验验证。不仅如此,本文还模拟残缺指纹的遗留环境,选取特定三角区域指纹作为待匹配图像进行指纹图像匹配。 3.1 数据集与实验环境 本文算法在Matlab 2015b进行实验,操作系统为Ubuntu 14.04,模型运行环境为Intel Xeon E5-2630@ 2.30 GHz,32 GB内存。选取的数据集来自FVC指纹竞赛,它提供来自不同的传感器采集的4个指纹数据库,该数据集可用于科学指纹实验的匹配、检索等。本文对小规模数据集FVC2002指纹库DB_1、DB_2进行了测试,它包含10枚不同手指的8次不同采样。 本文不仅在公开数据集上进行测试,还为了模拟真实犯罪情景,尤其是针对案发现场遗留的犯罪指纹进行测试。本文仿照实际案件中遗留三角区域指纹形成力度与角度,采用油墨捺印的方法采集,运用三星SCX-4100传感器进行扫描保存,生成300dpi指纹图像数据,如图3所示。真实数据在采集过程中,选取的格式一致,但大小不一。为了增强指纹图像的对比度,并且使算法具有普适性,对指纹库中的指纹图像只进行直方图均衡化处理,并未做其他处理。 Fig.3 Partial fingerprints simulating real case图3 仿照现场条件制作的残缺指纹 3.2 特征提取 由于残缺指纹图像的质量普遍不高,而二级特征点提取的准确性又关乎匹配算法的性能,本文采用二级特征点提取算法[10],主要步骤包括:图像增强,制作模板,寻找特征点,剔除错误匹配。提取结果如图4所示。本文还测试了算法[16],但是与前者相比,提取速度有所提升,但精确度不高。 Fig.4 Schematic diagram of minutiae extraction图4 特征点提取效果示意图 SIFT特征点运用公开的VLFeat库[17]进行提取,在提取之前只进行了直方图均衡化处理。由于残缺指纹图像的纹理特征是基于脊线走势、变化的细节特征,并且为了减少计算量,文献[18]指出了尺度参数大于3.5的SIFT特征点对匹配精度并没有提升作用,故本文只选取尺度参数小于3.5的SIFT特征点。此外,为了保证不同指纹图像提取到的SIFT数目相近,同时保留显著的SIFT特征点,因此设置峰值阈值去除低对比度特征点。峰值阈值在FVC2002数据库取0.03[18]。该阈值对最后的匹配精度影响较小,但是能加快匹配的速度。特征提取时间如表1所示。 Tabel 1 Comparison of features extraction time表1 特征提取时间比较 s 3.3 评价指标 本文旨在帮助现有指纹自动识别系统提升匹配精度,辅助公安部门从大规模指纹库中识别出罪犯指纹,提升匹配得分的置信度,因此本文选取的评价指标与FVC竞赛中的匹配算法标准指标略有不同。在FVC数据库中,不仅给出了平均拒识率(false rejection rate,FRR)、误识率(false accept rate,FAR)。还将每一幅图像作为查询,定义评价指标为: 其中,NC为排序前8幅图像中正确匹配的个数,该指标可以验证真正匹配的指纹是否出现在候选指纹列表前列。在真实三角图像数据中,由于每一幅图像只有一幅图像匹配,故类似地选取rank10-error作为评价指标。 4.1 FVC2002数据集 本文首先在FVC2002的DB_1、DB_2数据集上进行了测试,表2给出了基于相似三角形的匹配算法和基于SIFT匹配算法的查询结果。为了衡量模型的性能,本文给出的算法参数都经过栅栏搜索。由表2可以看出,相似三角形算法与SIFT匹配算法性能相近,而本文提出的改进三角形算法提升了算法[10]的性能,但提升效果有限。这说明指纹图像在采集过程中的旋转、平移和畸变,使得匹配算法并不能很好地区分出真正匹配的指纹。但如图5所示,基于SIFT特征点与基于相似三角形的匹配算法的搜索排序结果并不相同,即便基于相似三角形的算法效果弱于基于SIFT特征点的算法,但基于SIFT特征点算法匹配靠前的是纹理特征相近的图片,而基于相似三角形算法匹配的图片是二级特征点类似的图像,这意味着如果能从不同特征空间提取互补信息,能够有效提升残缺指纹的匹配准确性。 Tabel 2 Result of four kinds of algorithms on FVC2002表2 FVC2002数据库中4种算法结果比较 Fig.5 Relation graph of rank and accuracy on FVC2002 DB_2图5 FVC2002 DB_2数据库排序位置和准确率关系图 基于此,本文提出了STSF融合算法,在该次试验中,分别选取FVC2002的DB_2、DB_1互相作为训练集和测试集。FVC2002 DB_2数据集与DB_1类似,除在图像分辨率上略有不同之外,与DB_1基本类似,因此选取其作为训练集。实验结果表明,STSF算法在两个数据集上提升了接近5%的性能。 为了进一步对比不同指纹匹配得分与算法排序的关系,如图5、图6所示,本文给出了基于相似三角形、改进相似三角形、SIFT特征点以及STSF算法排序位置与匹配个数的关系。从图中可以看出,STSF算法明显好于其他算法,并且随着排序数目的增加,STSF算法仍然明显优于其他算法,说明STSF融合算法能够有效判别不同特征空间得分的置信度,进而提升得分函数的效能。 Fig.6 Relation graph of rank and accuracy on FVC2002 DB_1图6 FVC2002 DB_1数据库排序位置和准确率关系图 此外,给出了两个数据库上算法的FAR率和FRR率结果,如图7、图8、图9所示。实验表明,STSF能有效降低FAR率和FRR率。图10为不同特征下指纹查询结果。 Fig.7 FAR-FRR result of similar triangle algorithm on DB_1图7 DB_1中相似三角形算法的FAR-FRR图 4.2 真实数据实验结果 Fig.8 FAR-FRR result of SIFT algorithm on DB_1图8 DB_1中SIFT算法的FAR-FRR图 Fig.9 FAR-FRR result of STSF algorithm on DB_1图9 DB_1中STSF算法的FAR-FRR图 为了进一步说明本文算法在残缺指纹匹配上的有效性,选取真实采集的三角指纹数据进行实验。残缺三角指纹共有66个,将残缺指纹与完整指纹进行匹配,其中完整指纹包含51个正确匹配图像和49个错误匹配图像。与FVC2002数据集相比,采集的三角指纹畸变程度更高,图像清晰度更低。为了对比STSF算法的有效性,首先对比了全部66个查询图像的实验结果,由于测试数据有限,只选取了排序前10中出现的排序结果,实验结果如表3所示。由表3中可以看出,基于SIFT特征点匹配的算法和基于相似三角形的算法性能大幅降低。还对比了当前点匹配效果最好的算法HSOD(hybrid shape and orientation descriptor)[10],其算法的性能大大优于SIFT算法和基于改进的相似三角形算法,然而计算复杂度过高,每两幅指纹图像平均匹配时间达到40 s,是本文改进相似三角形算法的80倍,是SIFT匹配算法的285倍,不能满足实际需求。 在进行权重估计时采用了非参数统计方法——parzen窗估计算法。其算法复杂度主要由两部分组成,包括O(M)和O(n2),其中M为匹配次数,n为直方图箱宽。在FVC2002数据和真实数据中,n2>>M,因此算法复杂度为O(n2)。 Fig.10 Fingerprint search results on different features图10 不同特征下指纹查询结果图 Table 3 Results of three algorithms on real database表3 真实数据集中3种算法结果比较 为了进一步说明STSF算法的有效性,将真实采集的数据平分形成训练集和测试集。 不需要训练集的算法直接在测试集上进行算法性能评估。STSF算法只有一个参数,即直方图参数估计的箱体宽度,参数与算法性能的关系如图11所示。STSF算法能显著提升改进相似三角形和SIFT匹配特征点的匹配准确度,即便在改进相似三角形和SIFT特征点匹配算法性能相对较差的情况下,STSF算法也能显著提升匹配算法的性能,达到了与HSOD算法相差不多的结果。此外,还将STSF算法运用在HSOD和SIFT匹配算法上,即便在SIFT算法匹配性能十分差的情况下,贝叶斯判别算法也能提升算法的有效性,说明本文提出的STSF算法具有一定的鲁棒性。 Fig.11 Partial fingerprint searching result and histogram bin size图11 真实残缺指纹查询结果与直方图箱宽结果图 针对残缺指纹的匹配识别问题,由于指纹图像受采集环境影响,图像模糊,全局特征信息不足。因此,本文试图利用纹理信息和二级特征点信息进行匹配融合。由于不同特征空间的得分函数尺度不一,利用贝叶斯推断的方法能有效估计不同特征空间相似度的置信度,并依据此置信度进行特征融合。最后,选取数据集FVC2002和真实采集数据进行实验,提取相应的SIFT纹理特征和二级特征点作为匹配特征,试图从不同特征空间寻找真实匹配图像。实验结果表明:(1)纹理特征点空间和二级特征点空间反映了指纹图像的不同侧面,如果能提取二者的互补信息,能有效提升算法性能。(2)运用概率估计的方法能够有效判别当前特征空间得分的置信度,依据此置信度进行贝叶斯融合能够有效提升匹配算法的性能。 [1]Paulino A A,Feng Jianjiang,Jain A K.Latent fingerprint matching using descriptor-based Hough transform[J].IEEE Transactions on Information Forensics and Security,2013,8 (1):31-45. [2]Fu Xiang,Feng Jufu.Minutia tensor matrix:a new strategy for fingerprint matching[J].PloS One,2015,10(3):e0118910. [3]Singh V,Elamvazuthi I.Fingerprint matching algorithm for poor quality Images[J].The Journal of Engineering,2015,1. doi:10.1049/joe.2014.0247. [4]Nanni L,Lumini A.Descriptors for image-based fingerprint matchers[J].Expert Systems with Applications,2009,36 (10):12414-12422. [5]Cappelli R,Ferrara M,Maltoni D.Fingerprint indexing based on minutia cylinder-code[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(5):1051-1057. [6]Zheng Jiande,Gao Yuan,Zhang Mingzhi.Fingerprint matching algorithm based on similar vector triangle[C]//Proceedings of the 2nd International Congress on Image and Signal Processing,Tianjin,China,Oct 17-19,2009.Piscataway,USA:IEEE,2009:1-6. [7]Bazen A M,Gerez S H.Fingerprint matching by thin-plate spline modelling of elastic deformations[J].Pattern Recognition,2003,36(8):1859-1867. [8]Kisel A,Kochetkov A,Kranauskas J.Fingerprint minutiae matching without global alignment using local structures[J]. Informatica,2008,19(1):31-44. [9]Abraham J,Champod C,Lennard C,et al.Spatial analysis of corresponding fingerprint features from match and close non-match populations[J].Forensic Science International, 2013,230(1/3):87-98. [10]Abraham J,Kwan P,Gao Junbin.Fingerprint matching using a hybrid shape and orientation descriptor[M]//Yang Jucheng. State of the Art in Biometrics.Rijeka,Croatia:Intech, 2011:25-56. [11]Malathi S,Meena C.Improved partial fingerprint matching based on score level fusion using pore and SIFT features [C]//Proceedings of the 2011 International Conference on Process Automation,Control and Computing,Coimbatore, India,Jul 20-22,2011.Piscataway,USA:IEEE,2011:695-698. [12]Bhanu B,Tan Xuejun.Fingerprint indexing based on novel features of minutiae triplets[J].IEEE Transactions on PatternAnalysis and Machine Intelligence,2003,25(5):616-622. [13]Lele S,Richtsmeier J T.Euclidean distance matrix analysis: a coordinate-free approach for comparing biological shapes using landmark data[J].American Journal of Physical Anthropology,1991,86(3):415-427. [14]Jayaraman U,Gupta A K,Gupta P.An efficient minutiae based geometric hashing for fingerprint database[J].Neurocomputing,2014,137(5):115-126. [15]Choi H,Nagar A,Jain A K.On the evidential value of fingerprints[C]//Proceedings of the 2011 International Joint Conference on Biometrics,Washington,Oct 11-13,2011.Piscataway,USA:IEEE,2011:575-582. [16]Jain A,Hong Lin,Bolle R.On-line fingerprint verification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(4):302-314. [17]Vedaldi A,Fulkerson B.VLFeat:an open and portable library of computer vision algorithms[C]//Proceedings of the 18th International Conference on Multimedia,Firenze,Italy,Oct 25-29,2010.New York:ACM,2010:1469-1472. [18]Shuai Xin,Zhang Chao,Hao Pengwei.Fingerprint indexing based on composite set of reduced SIFT features[C]//Proceedings of the 19th International Conference on Pattern Recognition,Tampa,USA,Dec 8-11,2008.Piscataway,USA: IEEE,2008:2877-2880. 艾乐(1990—),女,北京人,2013年于湖北中医药大学获得硕士学位,现为中国人民公安大学博士研究生,主要研究领域为刑事科学技术痕迹检验。 ZHANG Zhizhong was born in 1991.He is a Ph.D.candidate at Institute of Automation,Chinese Academy of Sciences.His research interests include pattern recognition,computer vision and machine learning. 张志忠(1991—),男,杭州人,中国科学院自动化研究所博士研究生,主要研究领域为模式识别,计算机视觉,机器学习。 Study of Feature Fusion Matching STSFAlgorithm for Partial Delta Fingerprint* AI Le1+,ZHANG Zhizhong2 Most of the fingerprint matching algorithms used in automatic fingerprint identification systems(AFIS) are based on the accurate extraction of minutiae.However,when these methods are used to deal with highly distorted, rotational,and usually partial fingerprints collected from crime screen,their performance drops significantly.On the basis of similar triangle matching algorithm,this paper conquers scale problem by finding the positional relationship between SIFT(scale invariant feature transform)feature and second level feature.In addition,this paper also proposes a Bayesian statistical inference method to fuse the two kinds of algorithms,which is named as similar triangle SIFT feature(STSF)algorithm.The experimental results show that STSF algorithm effectively increases the precision and efficiency of partial fingerprints matching. fingerprint matching;feature fusion;partial fingerprint born in 1990.She the M.S.degree from Hubei University of Chinese Medicine in 2013.Now she is a Ph.D.candidate at PeopleƳs Public Security University of China.Her research interest is impression evidence examination in forensic science. A TP392 *The Fundamental Research Funds for PeopleƳs Public Security University of China under Grant No.2016JKF01102(中国人民公安大学基本科研业务费项目). Received 2016-11,Accepted 2017-03. CNKI网络优先出版:2017-04-01,http://kns.cnki.net/kcms/detail/11.5602.TP.20170401.1035.002.html



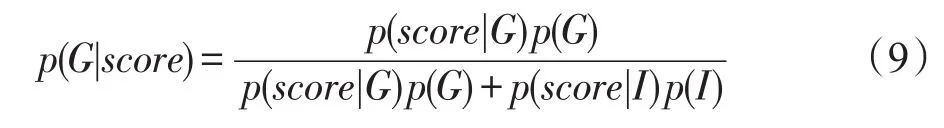
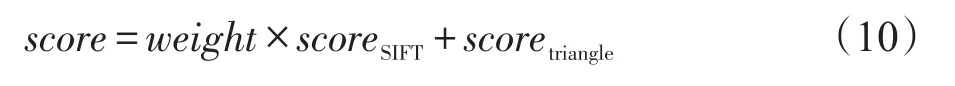

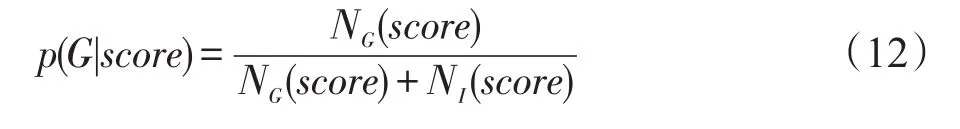
3 数据集选取及评价指标




4 实验及结果分析






5 结束语


1.Institute of Criminal Science and Technology,PeopleƳs Public Security University of China,Beijing 100038,China
2.State Key Laboratory of Management and Control for Complex Systems,Institute of Automation,Chinese Academy of Sciences,Beijing 100190,China
+Corresponding author:E-mail:zhuanmentianshu@163.com
