UC安全的自认证盲签密协议*
2017-06-15李建民俞惠芳
李建民,俞惠芳,赵 晨
青海师范大学 计算机学院,西宁 810008
UC安全的自认证盲签密协议*
李建民,俞惠芳+,赵 晨
青海师范大学 计算机学院,西宁 810008
LI Jianmin,YU Huifang,ZHAO Chen.Self-certified blind signcryption protocol with UC security.Journal of Frontiers of Computer Science and Technology,2017,11(6):932-940.
自认证盲签密(self-certified blind signcryption,SCBSC)协议能够同时实现公钥加密和盲签名,并且当发送方与接收方对签名存在争议时,任何第三方都能验证签名的有效性。然而,现有的自认证盲签密协议还不具有UC(universally composable)安全性,针对这个问题,引入UC安全框架,利用该框架可以模块化分析与设计自认证盲签密协议。定义了自认证盲签密协议在UC安全框架下对应的理想函数;证明了在适应性敌手模型下,自认证盲签密协议实现该理想函数,当且仅当签密协议满足不可区分适应性选择密文攻击(indistinguishability against adaptive chosen-ciphertext attacks,IND-CCA2)。
自认证盲签密;UC安全性;理想函数;适应性选择密文攻击
1 引言
1997年,Zheng提出的签密方案[1]能够在一个逻辑步骤内同时完成签名[2]和加密,相对于传统的先签名后加密来说,它的计算量和通信成本较低。2002年,Zheng等人[3]改进了1997年提出的签密方案,并对新方案给出了安全性定义和安全性证明。2011年,Fan等人[4]改进了2002版签密方案,改进方案在哈希函数的输入中添加了接收方和发送方的公钥。近年来,对于签密方案的研究一直都是现代密码学所关注的重点。将签密与一些特殊性质的签名结合起来,构造一些可以应用在不同的公钥密码体制上的签密体制。何俊杰等人[5]利用双线性对技术提出了一个基于身份签密方案。张宇等人[6]又进一步改进了基于身份签密方案。庞辽军等人[7]针对现有多接收者签密存在的接收者身份暴露和解密过程不公平等问题,提出了一个新的接收者签密方案。俞惠芳等人提出了基于无证书的盲签密方案[8]和使用自认证公钥的盲签密方案[9],同时进一步研究了混合签密方案[10]。虽然自认证思想结合签密方案的研究取得了一些成果,但研究还不够深入,特别是在对自认证盲签密方面的研究。
自认证盲签密不仅能够在一个逻辑步骤内同时完成盲签名和公钥加密功能,而且在发送方和接收方对密文的合法性产生争议时,任何第三方都可以验证签密的有效性。由于自认证盲签密本身的优点和越来越广泛的应用,使基于UC(universally composable)安全框架下实现其安全性很有必要。但是目前很少有这方面的研究,现有的自认证盲签密还不具有通用可组合安全性。
2001年,Canetti[11]提出了UC安全的概念。它的主要特点是满足协议的模块化设计要求,可以单独来设计协议,只要协议满足UC安全性,那么就可以保证和其他协议并发组合运行的安全性。设计一个UC安全的协议,首先要将协议所希望完成的功能抽象为一个理想函数,这个理想函数就相当于现实世界中一个不可攻破的可信第三方。而Canetti给出了在UC框架下被理想化的一些实现方案。2003年,Canetti等人在通用参考串模型中提出了通用可组合的两方和多方安全计算[12]。2008年,Kiayias等人[13]提出了能够抵抗自适应性攻击者UC安全的盲签名。2012年,Canetti等人[14]基于OT(oblivious transfer)协议的两方PAKE(password-authenticated key exchange)提出了该协议的理想功能,同时给出了基于OT协议构造一个双向认证PAKE协议的通用方法。在国内对UC安全的研究也取得了一些成果,如安全多方计算[15-16]、认证和密钥交换[17-18]、零知识[19]、数字签密[20]。
本文在已有的自认证盲签密协议[9]基础上,对UC安全框架进行了理论分析。首先定义了一般性的自认证盲签密协议,其次给出了UC安全框架下实现的自认证盲签密协议的理想函数的定义,然后给出了自认证盲签密协议的UC安全性与IND-CCA2(indistinguishability against adaptive chosen-ciphertext attacks)安全性之间的等价关系,最后给出具体协议实例和计算量分析。
2 基本概念
2.1 UC安全框架
UC安全框架由现实模型、理想模型和混合模型组成。在UC框架中使用交互式图灵机(interactive Turing machine,ITM)来表示协议的参与者、攻击者和环境机,并且每个ITM的运行都被限定在概率多项式时间内。如果说一个协议是UC安全的,那么对于任何敌手来说,环境机Z所看到的一切都可以在“理想世界”中看到。而在理想世界中,用户之间不用交互。现实协议所希望完成的任务可以通过访问理想功能来完成。
ITM:是一个标准的数学模型,它具有只读身份带、只读安全参数带、只读随机数带、输入带、输出带、输入通信带、输出通信带、工作带和一比特的激活带。选择用ITM来实现UC框架是因为它能够很好地表示交互和计算复杂性之间的关系,而且很好地融合了复杂理论中的标准模型,同时也很形象地表示了计算机的工作方式。
现实模型:描述了协议在现实环境中的执行情况,其中实体有协议π、参与方P1,P2,…,Pn、敌手A和环境机Z。参与方之间可以直接交互,而且都诚实地执行协议π,敌手A可以入侵参与者,一旦参与方Pi被敌手A入侵,则A将获得Pi的内部状态及以前的历史信息。
理想模型:描述了协议执行的理想情况,在此模型下协议可以得到无条件的安全,其中实体有虚拟参与方P1,P2…,Pn、仿真者S、环境机Z及理想函数F。理想模型与现实模型不同的是,虚拟参与方之间不能直接交互,只能通过理想函数F来转发消息。理想函数F只能和参与方Pi及敌手S进行通信,F是人们想要达到的安全目标,仿真者S与现实环境中的敌手A能力相当。
混合模型:是现实模型和理想模型的结合,其中实体有参与方P1,P2…,Pn、敌手A、环境机Z、协议π和理想函数F。与现实模型和理想模型不同的是,混合模型中不但有协议π,还有理想函数F的多个副本,且副本之间不传递消息。
根据文献[11]直接给出如下在UC安全框架下的定义。
定义1(不可区分性)两个二元分布X和Y是不可区分的(记为X≈Y),如果对于任何c∈N都存在k0∈N,使得所有满足k>k0及所有a,都有:

定义2(UC仿真)令F是一个理想函数,π是一个现实协议,如果对任何现实攻击者A都存在一个理想敌手S,则对于任何环境机Z都有:
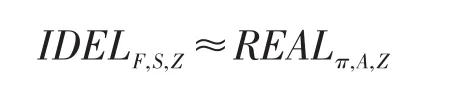
定义3(组合定理)令F和G是理想函数,π是F-混合模型下的一个协议,协议ρ在G-混合模型下可以安全地实现F。那么对于任何敌手AG,都存在一个AF,使得对于任何环境机Z,都有:

2.2 自认证盲签密协议
定义4[9]自认证盲签密协议(self-certified blind signcryption,SCBSC)由系统设置、用户注册、盲签密和解签密四部分组成。该协议的参与者有权威机构CA、消息拥有者M、盲签密者Pi和接收者Pj。算法描述如下。
(1)系统设置:该算法由CA执行。输入安全参数k,输出系统主密钥s和系统参数param,CA保密s,公开param。
(2)用户注册:输入系统参数param和用户U的身份IDU,输出(IDU,PU),这部分由U完成;输入(IDU,PU),输出QU和用户U的部分私钥xU,这部分由CA完成。
(3)盲签密:输入系统参数param、Qj、Pj、明文m和盲签密者Pi的私钥Si,输出密文σ=(X,Y,Z)。
(4)解签密:输入系统参数param、Qi、Pi及接收者的私钥Sj,输出明文或者失败。
2.3 IND-CCA2安全性
定义5[9]如果没有任何多项式有界的敌手A能够以一个不可忽略的概率赢得以下游戏,则称一个自认证盲签密协议在适应性选择密文攻击下具有不可区分性(IND-CCA2)。
假设攻击者A为一般用户,下面是攻击者A和挑战者Γ共同完成的游戏。
Γ使用安全参数k运行系统设置算法,得到主密钥和系统参数,并将系统参数发送给A。
阶段1在询问阶段,A向Γ请求如下询问。
密钥询问:A请求任意身份的公钥及私钥,Γ运行相应的算法,返回A所需要的请求值。
盲签密询问:A请求对任意消息m的关于身份IDi和IDj的盲签密者询问,Γ返回一个密文σ。
解签密询问:A选择两个身份IDi、IDj及密文σ,Γ计算身份IDj对应的私钥,并把解密的结果给A。
挑战阶段:A生成两个长度相同的明文m0、m1和希望挑战的两个身份IDi、IDj,身份IDj所对应的私钥不能被询问。Γ随机选取c∈{0,1},Γ执行对消息mc的盲签密算法,并将密文σ发给A,
阶段2A像阶段1那样执行询问,但是身份IDj所对应的私钥不能被执行询问,也不能对密文σ执行解密询问。
猜测阶段:Γ输出c′∈{0,1}对c的猜测。如果c′=c,则A赢得游戏。
2.4 UC框架下的自认证盲签密协议πSCBSC
一个具体的自认证盲签密协议通常是由一个可信的第三方CA来控制Setup和Extract算法。在UC安全框架模块化的设计下它没有定义好合适的功能接口。因此最主要的目标就是给出在UC框架下的自认证盲签密协议SCBSC的功能接口。
下面描述一般性的自认证盲签密协议πSCBSC= (Setup,Extract,Bsc,Dsc,Verify)。
Setup:系统参数生成算法,生成主密钥s和系统参数param。
Extract:密钥生成算法,生成签密者的密钥对(PKi,Si)和接收者的密钥对(PKj,Sj)。
Bsc:盲签密算法,通过(Bsc,sid,m,PKj)被签密参与方激活,运行Bsc(m)→σ。
Dsc:解签密算法,通过(Dsc,sid,σ,PKi)被解签密参与方激活,运行Dsc(σ)→m。
Verify:验证算法,在签密者否认自己的行为时,通过解密者给可信第三方(Verify,sid,m,σ)进行仲裁。
协议πSCBSC在UC框架下运行步骤如下:
当收到请求(CA,Setup,sid)后,首先验证sid= (CA,sid′),运行Setup(1k)→(s,param),并返回相应的参数param。
在收到某参与方Pi的请求(Key,sid,Pj)后,运行Extract(param,s,IDj)→(PKj,Sj),返回相应的产生值PKj。
在收到某参与方Pj的请求(Key,sid,Pi)后,运行Extract(param,s,IDi)→(PKi,Si),返回PKi。
在收到某参与方的请求(Bsc,sid,m,PKj)后,运行Bsc(param,sid,m,Si)→σ,得到盲签密σ。
在收到某参与方的请求(Dsc,sid,σ)后,运行Dsc(param,sid,σ,Sj)→m,得到消息m。
在收到某参与方的请求(Verify,sid,m,σ)后,运行Verify(m,σ)→f,并返回f的值。
3 理想函数FSCBSC
这里所定义的理想函数FSCBSC应该与协议πSCBSC有完全一样的接口。也就是说,希望理想函数FSCBSC在满足一定条件下能够被自认证盲签密协议SCBSC实现。理想函数FSCBSC的执行如下。
(1)系统设置
若收到来自某参与方的请求(CA,Setup,sid),验证sid=(CA,sid′),如果验证不成功,则忽略请求,否则,将此消息转发给理想敌手S,在得到理想敌手S回复的(Setup,Verify,sid,param)后,记录下算法Verify。
(2)用户注册
若收到来自盲签密者Pi的请求(Key,sid,Pj)后,将此消息转发给敌手S,在得到敌手S回复的(Pj,sid,PKj)时,将PKj发给参与者Pi。
若收到来自接收者Pj的请求(Key,sid,Pi)后,将此消息转发给敌手S,在得到敌手S回复的(Pi,sid,PKi)时,将PKi发给参与者Pj。之后,忽略所有的(Key,sid,Pi/Pj)。
(3)盲签密阶段
若收到参与方M的请求(Bsc,sid,m,PKj),验证sid= (Pi,sid′),如果验证不成功,则忽略发来的消息请求,否则,执行如下:
①如果参与方M是诚实的,那么M将通过(signcryption,sid)来通知盲签密者Pi和敌手S,并且要求产生一个签密,即Bsc(m)→σ,待盲签密者Pi和敌手S都同意的情况下,将签密消息(signcryption,sid,m,σ)发给M。
②如果参与方M是被收买过的,那么将会发送(Bsc,sid,m)给敌手S,并且从敌手S返回(signcryption,sid,m,σ),如果(m,σ,PKj,0)在之前已经被记录过,则取消当前的发送,然后把(signcryption,sid)发给Pi。
只要上述情况之一发生就记录(m,σ,PKj,1)。
(4)解签密阶段
若收到接收者Pj的请求(Dsc,sid,σ,PKi),验证sid= (Pj,sid′),如果验证不成功,则忽略发来的消息请求,否则,执行如下:
①如果记录过(m,σ),则设置f=1,并把(m,f)发给Pj。
②否则,将(Dsc,sid,σ,PKi)发给敌手S,并将敌手处返回的m以(m,f=0)的形式发给所有的参与者Pj。
(5)验证阶段
若收到参与方Pj的请求(Verify,sid,m,σ),验证sid=(Pj,sid′),如果验证不成功,则忽略发来的消息请求,否则,执行如下:
①如果已经记录过(m,σ),则设置f=1。(成功的签密)
②否则,如果参与者没有被敌手收买,则令f=0,并记录(m,σ,0)。(伪造签密)
③否则,令f=Verify(m,σ),且将(m,σ,f)记录下来。(敌手决定签密是否有效)
4 协议πSCBSC的安全性分析
定理1在适应性腐败敌手模型下,协议πSCBSC安全实现了理想函数FSCBSC,当且仅当自认证盲签密协议SCBSC满足IND-CCA2安全性。
证明(1)充分性。假如协议πSCBSC安全实现了FSCBSC,那么对于任何环境机都不可区分它是与(πSCBSC,A)交互还是与(FSCBSC,S)交互,则自认证盲签密协议SCBSC满足IND-CCA2安全性,即没有任何敌手A能够以不可忽略的概率赢得IND-CCA2游戏。
首先构造理想敌手S,运行过程如图1所示。
在收到FSCBSC的消息(CA,Setup,sid)后,运行参数生成算法Setup(1k)→(s,param),并返回相应的(Setup,Verify,param);否则,返回错误或不动作。
在收到FSCBSC发过来的消息(Key,sid,Pj)时,运行密钥生成算法Extract(param,s,IDj),产生(PKj,Sj),并返回产生值PKj。
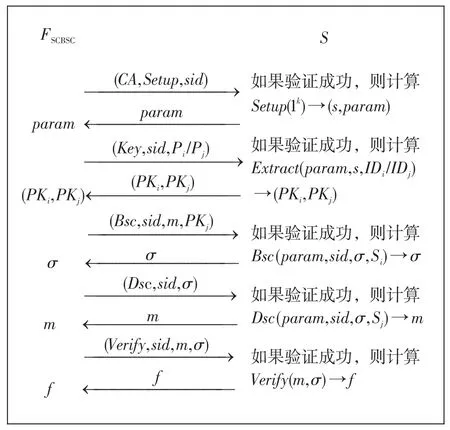
Fig.1 Running process of ideal adversaryS图1 理想敌手S的运行过程
在收到FSCBSC发过来的消息(Key,sid,Pi)时,运行Extract(param,s,IDi),产生(PKi,Si),并返回产生值PKi。
在收到FSCBSC的消息(Bsc,sid,m,PKj)时,如M是诚实的,则返回Bsc(param,sid,m,Si)→σ,并记录(m,σ);否则会收到FSCBSC发送的消息(Bsc,sid,m),并返回(signcryption,sid,m,σ)。
在收到FSCBSC的消息(Dsc,sid,σ)时,返回Dsc(param,sid,σ,Sj)→m。以(m,f=0)的形式发给所有参与者Pj;否则,将(m,f=1)发给Pj。
在收到FSCBSC的消息(Verify,sid,m,σ)时,返回Verify(m,σ)。如果参与者是被收买的,则令f=0,且记录(m,σ,0);否则,令f=1。
接下来证明仿真敌手S模拟了敌手A,构造如下IND-CCA2游戏中的敌手AZ,运行如图2所示。
在得到挑战者Γ的param后,激活Z。
在收到Z的请求(CA,Setup,sid)时,Γ以sid= (sid,param)回应。
在收到Z的请求(Key,sid,Pj)时,向挑战者发出(Extract,sid)请求,得到(PKj,Sj)应答。
在收到Z的请求(Key,sid,Pi)时,向挑战者发出(Extract,sid)请求,得到(PKi,Si)应答。

Fig.2 Running process ofAZin IND-CCAgame图2 IND-CCA游戏中AZ的运行过程
在收到Z的请求(Bsc,sid,m,PKj)时,向挑战者发(Bsc,sid,m,PKj)请求,挑战者Γ运行Bsc(param,sid,m,Si)→σ,并返回σ。
在收到Z的请求(Dsc,sid,σ,PKi)时,向挑战者发(Dsc,sid,σ)请求,然后挑战者Γ运行Dsc(param,sid,σ,Sj)→m,并返回m。
在收到Z的请求(Verify,sid,m,σ)时,运行Verify(param,m,σ)→f并返回f,当f=1时,签密成功;否则是伪造的消息签密或者是由敌手来决定签密是否有效。
当Z停止时,输出失败并停止。
显然,当AZ验证成功时,也就是AZ在定义5的IND-CCA2游戏中成功猜对了c′=c。此时,环境Z与(πSCBSC,A)交互和与(FSCBSC,S)交互时的情况是完全一样的。换句话说,如果环境Z以概率|Pr(Z(πSCBSC,A))→1-Pr(Z(FSCBSC,S))→1|区分它是与(πSCBSC,A)交互还是与(FSCBSC,S)交互(在现实世界中Pr(Z(πSCBSC,A))→1是一个可忽略的概率,而理想世界中Pr(Z(FSCBSC,S))→1总是等于0),则AZ将以概率|Pr(Z(πSCBSC,A))→1-Pr(Z(FSCBSC,S))→1|赢得IND-CCA2游戏。
(2)必要性。如果协议SCBSC是IND-CCA2安全的,即没有任何敌手A以不可忽略的概率赢得IND-CCA2游戏,则协议πSCBSC安全实现了FSCBSC,即对于任何环境ZA不可区分它是与(πSCBSC,A)交互还是与(FSCBSC,S)交互。构造这样的一个环境机ZA运行如下。
ZA首先给协议发Setup请求,在收到sid回复后,将param作为输入启动A。
对于A的请求(Extract,sid),ZA可以先向协议发(CA,Setup,sid),再发(Key,sid,Pj),得到盲签密者Pi的密钥对,把后者的值返回给A,同样可得到接收者Pj的密钥对,把相应值返回给A。
对于A的请求(Bsc,sid,m),ZA可以先向协议发(CA,Setup,sid),再发(Key,sid,Pj),最后发相应的(Bsc,sid,m,PKj),以后者的返回值回应A。
对于A的请求(Dsc,sid,σ),ZA可以先向协议发(CA,Setup,sid),再发(Key,sid,Pj),最后发相应的(Dsc,sid,σ)请求,将后者的返回值发给A。
当A输出(m′,σ′)时,检验(m′,σ′)是否为合法的签密,则对协议发送请求(Verify,sid,m′,σ′),输出返回值f。
显然在现实世界中,ZA输出1的概率正是A赢得IND-CCA2游戏的概率。而在理想世界中,ZA总是输出0。也就是说,在现实模型当中,当敌手A以一个可忽略的概率赢得IND-CCA2游戏时,则ZA是以一个可忽略的概率输出1,在理想模型当中,ZA输出1的概率为0。 □
5 具体协议实例
上面证明了一般性的自认证盲签密协议是具有UC安全性的,根据前面设计的一般性的自认证盲签密协议πSCBSC,现在结合已有的自认证盲签密协议[9]给出具体协议实例。下面描述中CA是可信第三方,M是消息拥有者,Pi是盲签密者,Pj是接收者。
参数设置:sid为会话标识,k为安全参数,G1、G2分别是阶为q的加法群和乘法群,P是G1的生成元,e是G1×G2→G2的双线性对映射。H0:{0,1}*×是3个哈希函数。
若收到消息(CA,sid,Setup),则参与方CA选取主密钥计算系统公钥PCA=sP,并且公开参数
若收到消息(Key,sid,Pi),则Pi选取计算PKi=riP,将(IDi,PKi)发给CA,CA计算Qi=H0(IDi,Pi),xi=sQi,然后返回(IDi,Qi,xi)给Pi,Pi计算Si=riQi+xi,并公开PKi。
若收到消息(Key,sid,Pj),则Pi选取计算PKj=rjP,将(IDj,PKj)发给CA,CA计算Qj=H0(IDj,Pj),xj=sQj,然后返回(IDj,Qj,xj)给Pj,Pj计算Sj=rjQj+xj,并公开PKj。
若收到消息(Bsc,sid,m),并且会从Pj处收到PKj,Pi选取密值计算将(R,V)发给M。M随机选取密值计算X=aR,ω=Va,Y=H2(ω)⊕m,h=aH1(m,X)。随后将h发给Pi,Pi计算W=k-1hSi,然后再发给M。最后M将(X,Y,Z)发给接收者Pj。
若收到某个参与方的消息(Dsc,sid,m,PKj),并且会从Pi处收到PKi,Pj计算ω=e(X,Sj),m=H2(ω)⊕Y,然后验证等式是否成立,若成立,则令f=1,盲签密合法;否则认为盲签密不合法。
若收到消息(Verify,sid,(m,X,Z)),公开计算X′=aR,H1′=H1(m,X′),然后验证等式是否成立。如果等式成立,那么盲签密者Pi的盲签密(X,Y)和公钥PKi同时被认证,并且接收者Pj认为(X,Y)就是盲签密者Pi对消息m的合法盲签密。否则,(X,Y)不合法。
6 计算量分析
在公钥密码体系中,一般用基于身份的方法、基于证书的方法、基于无证书的方法和基于自认证的方法来认证用户的公钥,一般用基于双线性对问题、离散对数问题(discrete logarithm problem,DLP)、椭圆曲线离散对数问题(elliptic curve discrete logarithm problem,ECDLP)来研究自认证公钥环境下的签密协议。本文给出的协议实例是基于双线性对来设计的自认证盲签密协议,下面给出该协议实例和其他协议的效率比较,考虑双线性对预处理,如表1所示。
P表示G1上的双线性对运算,M表示G1上的标量乘,E表示G2上的指数运算,H表示哈希函数。如果设一次G1上的标量乘为单位时间tm,那么根据文献[21]的总结,可以得到如下关系:P≈1 440tm,H≈23tm,E≈21tm,M≈tm。
从效率上来分析,文献[2]总开销为2 909tm,文献[5]为3084tm,文献[6]为1581tm,文献[8]为4520tm,本文为3 016tm。显然,本文实例明显优于文献[8],与文献[2,5]效率相当。但是相对于文献[2]来说,本文协议实例使用了签密技术,即签名的同时也对消息进行了加密,而相对于文献[5],本文协议实例增加了消息的盲性,提高了安全性。与文献[6]比较,本文效率稍低,但是本文协议实例在增加了消息盲性的同时,还很好地解决了基于身份签密中存在的秘钥托管问题。综合来讲,自认证盲签密协议还是非常不错的。
7 结束语
本文在UC框架下设计了一般性的自认证盲签密协议πSCBSC,形式化定义了在UC框架下的自认证盲签密协议的理想函数FSCBSC。在适应性腐败敌手模型下,给出了自认证盲签密协议的UC安全性与IND-CCA2安全性之间的等价关系。未来研究计划之一是签密密钥封装机制的通用可复合安全性。

Table 1 Efficiency of this paper compared with other literatures表1 本文方案与其他文献的效率比较
[1]Zheng Yuliang.Digital signcryption or how to achieve cost (signature&encryption)≪ cost(signature)+cost(encryption)[C]//LNCS 1294:Proceedings of the 17th Annual International Cryptology Conference,Santa Barbara,USA,Aug 17-21,1997.Berlin,Heidelberg:Springer,1997:165-179.
[2]Tang Pengzhi,Liu Qiwen,Zuo Liming.A modified scheme of partially blind signature based on ID[J].Computer Engineering,2015,41(10):139-143.
[3]Baek J,Steinfeld R,Zheng Yuliang.Formal proofs for the security of signcryption[C]//LNCS 2274:Proceedings of the 5th International Workshop on Practice and Theory in Public Key Cryptosystems:Public Key Cryptography,Paris, Feb 12-14,2002.Berlin,Heidelberg:Springer,2002:80-98.
[4]Fan Jia,Zheng Yuliang,Tang Xiaohu.A single key pair is adequate for the Zheng signcryption[C]//LNCS 6812:Proceedings of the 16th Australasian Conference on Information Security and Privacy,Melbourne,Australia,Jul 11-13, 2011.Berlin,Heidelberg:Springer,2011:371-388.
[5]He Junjie,Jiao Shuyun,Qi Chuanda.Analysis and improvement of ID-based signcryption scheme[J].Application Research of Computers,2013,30(3):913-920.
[6]ZhangYu,Du Ruiying,Chen Jing,et al.Analysis and improvement of an identity-based signcryption[J].Journal on Communications,2015,36(11):174-179.
[7]Pang Liaojun,Li Huixian,Cui Jingjing,et al.Design and analysis of a fair ID-based multi-receiver anonymous signcryption[J].Journal of Software,2014,25(10):2409-2420.
[8]Yu Huifang,Wang Caifen,Yang Lin,et al.Certificateless based blind signcrption scheme[J].Computer Applications and Software,2010,27(7):71-73.
[9]Yu Huifang,Wang Caifen.Self-certified signcryption scheme [J].Journal of ComputerApplications,2009,26(9):3508-3511.
[10]Yu Huifang.Study on provably secure theory for hybrid signcryption[D].Xi’an:Shaanxi Normal University,2015.
[11]Canetti R.Universally composable security:a new paradigm for cryptographic protocols[C]//Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science,Las Vegas,USA,Oct 14-17,2001.Washington:IEEE Computer Society,2001:136-145.
[12]Canetti R,Lindaell Y,Ostrovsky R,et al.Universally composable two-party and multi-party secure computation[C]// Proceedings of the 34th Annual ACM Symposium on Theory of Computing,Montreal,Canada,May 19-21,2002.New York:ACM,2003:494-503.
[13]Kiayias A,Zhou Hongsheng.Equivocal blind signature and adaptive UC-security[C]//LNCS 4948:Proceedings of the 5th Theory of Cryptography Conference,New York,Mar 19-21,2008.Berlin,Heidelberg:Springer,2008:340-355.
[14]Canetti R,Dachman-Soled D,Vaikuntanathan V,et al.Efficient password authenticated key exchange via oblivious transfer[C]//LNCS 7293:Proceedings of the 15th International Conference on Practice and Theory in Public Key Cryptography,Darmstadt,Germany,May 21-23,2012.Berlin,Heidelberg:Springer,2012:449-466.
[15]Lei Feiyu.Studies on UC secure multiparty computation and its application[D].Shanghai:Shanghai Jiaotong University,2007.
[16]Tian Youliang,Peng Changgen,Ma Jianfeng,et al.Universally composable secure multiparty computation protocol with fairness[J].Journal on Communication,2014,35(2): 54-62.
[17]Wang Zhu,Dai Yiqi,Ye Dingfeng.Universally composable identity-based signature[J].Acta Electraonica Sinica,2011, 39(7):1613-1617.
[18]Zhang Zinan,Guo Yuanbo,Yang Kuiwu,et al.Universally composable security authenticated key exchange protocol [J].Journal of Xidian University,2014,41(5):185-191.
[19]Wang Zhu,Dai Yiqi.Ideal functionality and sequential composition of zeroknowledge[J].Information Security and Communications Privacy,2012(6):84-86.
[20]Tian Youliang,Ma Jianfeng,Peng Changgen,et al.Universally composable mechanism for group communication[J]. Chinese Journal of Computers,2012,35(4):645-646.
[21]Fan I,Sun W Z,Huang S M.Provably secure randomized blind signature schemes based on bilinearpairing[J].Computers and Mathmatics withApplication,2010,60(2):285-293.
附中文参考文献
[2]汤鹏志,刘启文,左黎明.一种基于身份的部分盲签名改进方案[J].计算机工程,2015,41(10):139-143.
[5]何俊杰,焦淑云,祁传达.一个基于身份的签密方案的分析与改进[J].计算机应用研究,2013,30(3):913-920.
[6]张宇,杜瑞颖,陈晶,等.对于一个基于身份签密方案的分析与改进[J].通信学报,2015,36(11):174-179.
[7]庞辽军,李慧贤,崔静静,等.公平的基于身份的多接收者匿名签密设计与分析[J].软件学报,2014,25(10):2409-2420.
[8]俞惠芳,王彩芬,杨林,等.基于无证书的盲签密方案[J].计算机应用与软件,2010,27(7):71-73.
[9]俞惠芳,王彩芬.使用自认证公钥的盲签密方案[J].计算机应用,2009,26(9):3508-3511.
[10]俞惠芳.混合签密及其可证明安全性理论研究[D].西安:陕西师范大学,2015.
[15]雷飞宇.UC安全多方计算模型及其典型应用研究[D].上海:上海交通大学,2007.
[16]田友亮,彭长根,马建峰,等.通用可组合公平安全多方计算协议[J].通信学报,2014,35(2):54-62.
[17]王竹,戴一奇,叶顶峰.普适安全的基于身份的签名机制[J].电子学报,2011,39(7):1613-1617.
[18]张紫楠,郭渊博,杨奎武,等.通用可组合认证密钥交换协议[J].西安电子科技大学学报,2014,41(5):185-191.
[19]王竹,戴一奇.零知识的理想功能和零知识的序列组合[J].信息安全与通信保密,2012(6):84-86.
[20]田有亮,马建峰,彭长根,等.群组通信的通用可组合机制[J].计算机学报,2012,35(4):645-646.

LI Jianmin was born in 1991.He is an M.S.candidate at School of Computer,Qinghai Normal University.His research interests include information security and cryptography.
李建民(1991—),男,湖南怀化人,青海师范大学计算机学院硕士研究生,主要研究领域为信息安全,密码学。

俞惠芳(1972—),女,青海乐都人,博士,青海师范大学教授、硕士生导师,主要研究领域为密码学,信息安全。已完成973前期专项等10余项,主持在研国家自然基金项目2项,发表学术论文40余篇,出版著作1部。
ZHAO Chen was born in 1992.She is an M.S.candidate at School of Computer,Qinghai Normal University.Her research interests include information security and cryptography.
赵晨(1992—),女,河南南阳人,青海师范大学计算机学院硕士研究生,主要研究领域为信息安全,密码学。
Self-Certified Blind Signcryption Protocol with UC Security*
LI Jianmin,YU Huifang+,ZHAO Chen
School of Computer,Qinghai Normal University,Xining 810008,China
+Corresponding author:E-mail:yuhuifang@qhnu.edu.cn
Self-certified blind signcryption(SCBSC)protocol can simultaneously fulfill public key encryption and blind signature.When disputation occurs between the sender and recipient,any third party can verify the validity of the signature.However,the existing self-certified blind signcryption protocol does not yet have universally composable(UC)security.Aiming at this problem,the UC security framework is introduced.The use of this framework can analyze and design self-certified blind signcryption protocol in modularity.Firstly,the ideal function of self-certified blind signcryption protocol is defined under the UC security framework;secondly,under the adaptive adversary model,self-certified blind signcryption protocol may achieve functionality,if and only if self-certified blind signcryption protocol satisfies the indistinguishability against adaptive chosen-ciphertext attacks(IND-CCA2)
self-certified blind signcryption;UC security;ideal function;adaptive chosen-ciphertext attacks
g was born in 1972.She
the Ph.D.degree from Shaanxi Normal university.Now she is a professor and M.S.supervisor at Qinghai Normal University.Her research interests include cryptography and information security. She has completed more than 10 research projects including 973 basic research program.She is managing 2 research projects including the National Natural Science Foundation of China.She has published more than 40 papers and 1 work.
A
TP309
*The National Natural Science Foundation of China under Grant No.61363080(国家自然科学基金);the Basic Research Project of Qinghai Province under Grant No.2016-ZJ-776(青海省应用基础研究项目).
Received 2016-05,Accepted 2016-09.
CNKI网络优先出版:2016-09-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160908.1045.008.html
