基于白光干涉法测量微光栅形貌及相关几何参量的研究
2017-06-14牛渊张敏王俊杰徐永祥
牛渊+张敏+王俊杰+徐永祥
摘要:基于显微白光干涉术,利用扫描干涉显微镜对四台阶面阵微光栅记录了128幅白光干涉图,并分别运用重心法、空间频域算法、移相算法及包络曲线拟合法对扫描干涉图进行了分析处理。被测微光栅的形貌及周期在各算法下均完全吻合,台阶总高最大相差0.8%。同时,用美国Veeco白光轮廓仪对同一样品的形貌及光栅周期进行了测试,数据显示两者结果非常吻合,仅台阶总高相差0.7%。研究结果表明,所采用的四种算法均适用于微观三维形貌的测量。
关键词: 白光干涉; 干涉显微镜; 重心法; 空间频域算法; 移相算法; 包络曲线拟合法; 微光栅
中图分类号: O 43 文献标志码: A doi: 10.3969/j.issn.1005-5630.2017.02.001
文章编号: 1005-5630(2017)02-0001-07
引 言
微光栅是一种重要的二元光学元件,它在航空航天、国防科技、信息处理、微光机电等领域均有着重要应用[1-2]。影响微光栅工作性能的基本参量包括微轮廓形貌、光栅周期、台阶数和台阶高度等,因而如何准确测量这些参量进而判断其是否满足设计指标就具有研究价值。
一般而言,对微光栅周期和台阶高度等参数可以通过测量其形貌获得,而微光栅形貌的测量则属于三维微形貌测量的范畴。目前对微观形貌的测量可分为接触式和非接触式两大类[3]:前者包括触针式测量法[4]、扫描探针显微镜法[5]等;后者通常采用的是光学测量方式,包括干涉显微镜法[6-7]、聚焦检测法[8]等。在非接触式测量中,基于单色光照明的显微移相干涉术是国内外公认也是现今运用非常普及的一项高精度测量技术,但它有个适用的前提,即相邻像素所对应物面两点的形貌高度要满足≤λ/4(λ为光波长),否则由于相位重构的不确定性而可能出现错误。由于白光具有相干长度接近于零的特点,因此采用白光干涉术可有效解决上述相位模糊问题。用白光扫描干涉进行形貌测量时,核心是要确定不同物点所对应的零光程差位置,而确定零光程差位置的方法又有数种[9],包括重心法[10-11]、空间频域算法[12]、移相算法[13-14]、包络曲线拟合法[15]等。本文对基于白光干涉术扫描得到的128幅干涉图分别运用四种算法进行编程处理,得到了不同算法下的结果,并进行了分析比较。
1 算法原理
1.1 重心法
理想的白光干涉信号以零光程差点为中心左右对称分布,因此重心法通过计算信号的重心来确定零光程差位置。实际由于噪声等因素的影响,信号左右并不完全对称。重心法分两步:粗定位和精定位。粗定位的目的是找到灰度值最大的点,精定位计算式为
1.4 包络曲线拟合法
利用Fourier变换滤波提取包络的方法是:首先对信号作离散Fourier变换,取出其频谱的正一级旁瓣,将其左移至频谱的原点,并作逆Fourier变换,就得到信号的包络图。进而根据包络图算得离散点中最大灰度值所对应的扫描序号,并在其前后取若干个强度值进行二次曲线拟合,由二次曲线的最高点得到相应的扫描序号j,最后按式(2)计算即可得到相对高度值。
2 测量装置与调节步骤
图1为测量装置实物图,图2为其工作原理图。由卤钨灯发出的白光经聚光镜组会聚至孔径光阑,再经视场光阑和准直物镜成为平行光。平行光由分光镜反射进入Mirau干涉物镜,并通过分光板分为两束光:一束由分光板反射后到达参考板,经反射后回到物镜;另一束透过分光板射向被测的微光栅表面,经反射后由分光板回到Mirau物镜。两束光在CCD靶面发生干涉,CCD记录的干涉图通过图像卡实现A/D转换并保存在计算机内。计算机输出的比特数经驱动电源放大后,由压电陶瓷(PZT)作用于样品台,从而实现对被测样品的扫描。
实验时主要调节步骤如下:
(1) 将待测的微光栅(编号GP016,成都纳光科技有限公司生产,实物图参见图3)置于载物台上,镜头对准微光栅;
(2) 对被测微光栅调焦,并设定合适的起始位置,取步长50 nm,扫描采集128幅干涉图并保存;
(3) 取出微光栅,将图4所示的光栅尺(50 μm /线对)置于样品台上,重新调焦并记录其显微图像。
3 数据处理与结果
对所得128幅扫描干涉图,从同一点开始截取512像素×512像素(接近四个周期性单元)的大小,并分别按上述四种算法进行编程处理,得到各算法下形貌结果(共含四个台阶面)。鉴于各台阶面存在少量倾斜,需对每一台阶面用倾斜平面进行拟合并消去倾斜,此时相邻两台阶面的相对高度差值即为台阶高度。此外,按每一算法计算时:台阶高度均按各像素点所对应的高度差的平均值作为该算法下的台阶高度,不规则边缘除外;光栅周期则根据形貌结果取两方向上对应点距离的平均作为测量结果;两方向的实际坐标由“像素间隔×物像转换系数”求得。现就各算法所得的主要过程与结果分别做一简述。
(1) 重心法
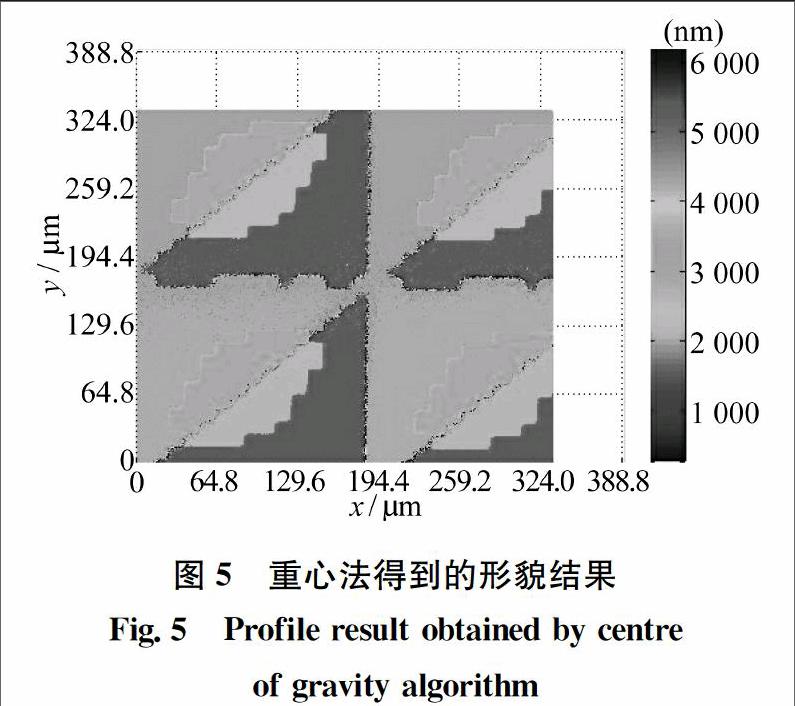
用重心法得到的形貌结果如图5所示。
(2) 空間频域算法
以像素点(1,1)为例。从扫描强度的离散Fourier变换的正一级旁瓣内取出相对强度较大的五个数据点,对应的扫描序号为20~24,实际kj的大小为
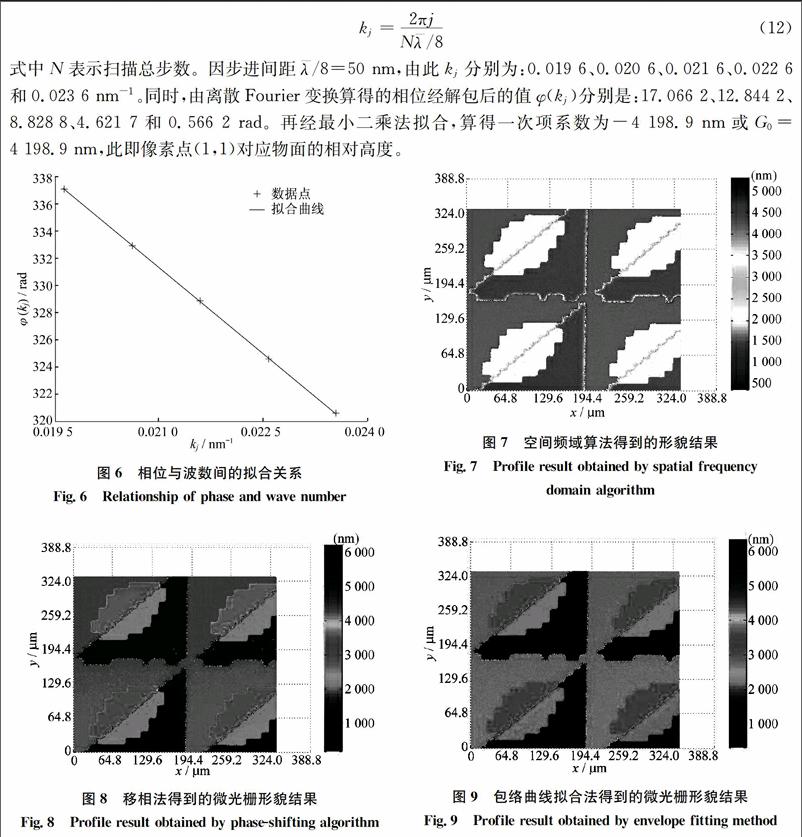
式中N表示扫描总步数。因步进间距λ—/8=50 nm,由此kj分别为:0.019 6、0.020 6、0.021 6、0.022 6和0.023 6 nm-1。同时,由离散Fourier变换算得的相位经解包后的值φ(kj)分别是:17.066 2、12.844 2、8.828 8、4.621 7和0.566 2 rad。再经最小二乘法拟合,算得一次项系数为-4 198.9 nm或G0=4 198.9 nm,此即像素点(1,1)对应物面的相对高度。
图6是波数kj与相位φ(kj)间的离散关系。可以看出,φ(kj)与kj间呈现良好的线性关系,表明测量系统中二阶以上的色散影响极小,完全可以忽略。
该算法下得到的微光栅形貌如图7所示。
(3) 移相算法
经移相算法得到的微光栅形貌如图8所示。
(4) 包络曲线拟合法
同样仅以像素点(1,1)为例。经Fourier逆变换得到强度分布,算得离散点中最大灰度值对应的扫描序号为83,取扫描序号81~85范围内的离散点强度作二次函数拟合,经计算最大值点对应的横坐标为83.2,此即扫描序号,相应物点的相对高度h=4 160.0 nm。得到的形貌如图9所示。
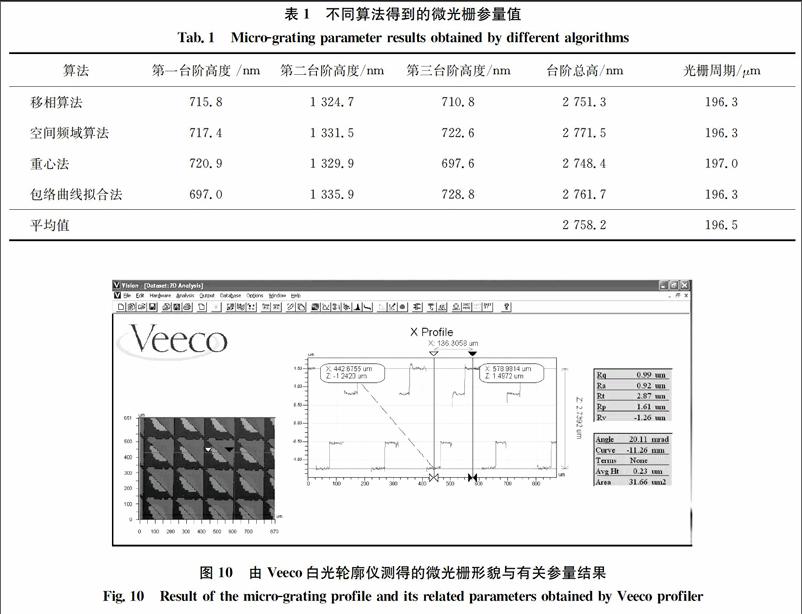
表1给出了各算法下的光栅周期与台阶高度结果。为作比较,本文还利用美国Veeco白光轮廓仪对该微光栅进行了测试,得到光栅的总高为2 739.2 nm,周期为196.3 μm,形貌如图10所示。经比较可以看出:(1) 由本文不同算法得到的微光栅形貌结果完全一致,均表明被测对象为四台阶面阵式周期性结构,形貌结果也与Veeco所得结果彼此吻合;(2) 由各不同算法得到的光栅周期结果彼此吻合良好,其均值与Veeco轮廓仪测得的结果仅相差0.2 μm;(3) 不同算法下的台阶高度结果彼此稍有一定差异,其中,最大与最小台阶总高彼此相差约0.8%,平均臺阶总高与Veeco结果相差0.7%。
4 误差分析
不同算法下产生的测量误差可以归结为三个方面:算法误差、装置误差和调节误差。算法误差取决于不同算法下的算法精度。装置误差则主要来源于两方面:一是PZT驱动样品实现等间隔扫描(理想扫描步长为50 nm)时的微位移误差,二是CCD各单元响应的非线性以及不同单元响应的不一致。调节误差是指为得到物像转换系数对光栅尺进行调焦时存在的离焦误差。
5 结 论
(1) 由本文不同算法得到的微光栅形貌及其周期完全吻合,也与Veeco测得的结果吻合良好;
(2) 由各分析算法测得的微光栅台阶总高最大相差0.8%,平均总高与Veeco所得结果相差0.7%,大致吻合;
(3) 当利用空间频域算法进行分析时,完全可以忽略测量系统中二阶以上的色散;
(4) 本文所采用的四种测量算法完全适用于微观三维形貌的测量。
本文研究的虽然是微光栅形貌测量方法,但此测量方法也适用于宏观物体的形貌测量,为精密物件的测量提供了一种新的途径。
参考文献:
[1] KEMME S A.微光学和纳米光学制造技术[M].周海宪,程云芳,译.北京:机械工业出版社,2012.
[2] 赫尔齐克H P.微光学元件、系统和应用[M].周海宪,译.北京:国防工业出版社,2002.
[3] 徐永祥,张乾方,刘松松,等.基于空间频域算法的三维微观形貌的测量[J].光电工程,2014,41(8):1621.
[4] SONG J F,VORBURGER T V.Stylus profiling at high resolution and low force[J].Applied Optics,1991,30(1):4250.
[5] 李剑白,李达成,李小芸,等.原子力显微镜测试光学超光滑表面微轮廓的研究[J].光学学报,2000,20(11):15331537.
[6] 徐永祥,陈磊,朱日宏,等.微小球面曲率半径的测量研究[J].仪器仪表学报,2006,27(9):11591162.
[7] 周攀,于瀛洁.基于白光扫描轮廓仪的算法研究[J].仪器仪表学报,2002,23(增刊2):533535.
[8] 孔健,万德安.表面微观形貌测量中的光聚焦检测法[J].上海机床,2000(1):2830.
[9] 杨天博,郭宏,李达成.白光扫描干涉测量算法综述[J].光学技术,2006,32(1):115117.
[10] CHEN S,PALMER A W,GRATTAN K T V,et al.Digital signal-processing techniques for electronically scanned optical-fiber white-light interferometry[J].Applied Optics,1992,31(28):60036010.
[11] 耿东锋,何英杰,苏宏毅.透明台阶的白光干涉测量方法研究[J].光学仪器,2013,35(6):7477.
[12] DE GROOT P,DECK L.Surface profiling by analysis of white-light interferograms in the spatial frequency domain[J].Journal of Modern Optics,1995,42(2):389401.
[13] SANDOZ P,DEVILLERS R,PLATA A.Unambiguous profilometry by fringe-order identification in white-light phase-shifting interferometry[J].Journal of Modern Optics,1997,44(3):519534.
[14] 孙杰,刘铁根,张以谟,等.白光干涉零光程差位置四步测量法及其精度分析[J].天津大学学报,2004,37(4):363367.
[15] CHIM S S C,KINO G S.Three-dimensional image realization in interference microscopy[J].Applied Optics,1992,31(14):25502553.
(编辑:刘铁英)
