T接输电线路故障精确定位方法研究

周超凡，鄢发齐，周良松，姚占东，沈宇亮

（1.国家电网公司华中电力调控分中心，湖北 武汉 430077；2.华中科技大学电气与电子工程学院，湖北 武汉 430074）

0 引言

输电线路在电力系统中担负着电能传输的重任，T型接线相比普通双端接线输送能力增加、节约走廊占地，在中国电网输电线路接线方式中所占比例越来越高[1]。T接输电线路暴露野外，易遭受雷电、雾霾、覆冰等恶劣环境因素而发生跳闸故障，由于T接输电线路输电功率高、负载重，其T接支线常常连接一些重要供电单位，一旦发生故障将造成比普通线路更大的损失，因此及时修复线路故障对电力系统安全稳定运行相当重要[1-3]。但是工程实际中，巡线困难，若遇到大风暴雪雷雨等天气，更会使巡线工作困难异常；另一方面，现有的快速保护装置使得大部分故障没有明显破坏痕迹，故障位置比较隐蔽，更为现场巡线工作带来了相当大的困难。由于发生故障所在地区常常交通不便，加之保护装置快速发展使得故障痕迹不明显，现场巡线工作很难开展[4,5]。因此，如果能提前准确预知T接输电线路故障点，不仅可以有效指导现场巡线工作，及时修复线路，恢复电力供应，而且可及时发现T接输电线路的潜在隐患和薄弱环节，增强输电线路运行可靠性[6]。

目前研究比较广泛输电线路故障精确定位技术主要是基于工频测距与行波测距两大原理，因为T接点不连续点的介入，导致线路阻抗不连续，因而工频测距很难适用于复杂的T接输电线路，而行波定位技术可实现复杂T接输电线路故障点精确定位[7]。但是因为T接输电线路网络拓扑结构的特殊性，其行波折反射较为复杂，目前应用较好的基于行波测距技术的T接输电线路故障定位系统，无论是监测电压行波还是监测电流行波，均需要在三端变电站安装监测仪，经济性不高，难以推广应用，但是一旦减少监测装置，故障点定位精度将会大大降低[8]。

在这样的生产实践迫切需要前提下，开展T接输电线路故障点精确故障定位研究工作。通过分析T接输电线路三端电流相位差动原理，按照先实现故障支线判别、再完成故障点精确定位的路线，最终提取出T接输电线路故障点精确定位方法。

1 T接输电线路三端电流相位差动原理

本文采用T接输电线路发生故障时的电流故障分量系统进行分析，如图1所示，假设AT支路发生故障，其中F1故障点为外部故障，F2故障点为内部故障，电流方向规定为从母线指向线路。

图1 T接输电线路故障分量图Fig.1 Fault component diagram of T-connected transmission line

如果不考虑故障电流在各支路传播的时间差，不考虑各相关阻抗的阻抗角差异，则可得出三端电流同相角，当线路发生F1外部故障，即三端电流无相差的结论；当线路F2点发生内部故障，则可得出B、C端故障电流无相差，与A端故障电流相反的结论[9]。但是实际运行中，由于分布电容的存在，加之各端阻抗角不可能完全保持相同，各端电流很难再保持理想条件下的关系。为此，需要进一步讨论实际运行中故障条件下三端电流关系，为了方便讨论暂不考虑分布电容的影响。

1.1 内部故障时三端电流关系讨论分析

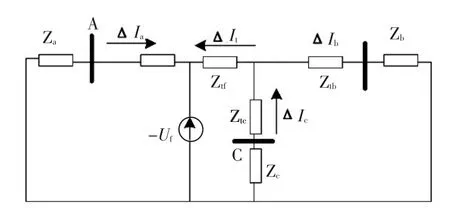
图2 T接输电线路内部故障时故障分量系统Fig .2 Internal failure component system of T-connected transmission line

如图2所示，当发生内部故障时，则三端电流△Ia、△Ib、△Ic存在如式（1）和（2）的关系，其中Zb∑=Zb+Ztb、Zc∑=Zc+Ztc。

由内部故障时三端电流的表达式知，三端电流的电流相位差异完全取决于相关各阻抗的阻抗角差异。当理想情况下，忽略各阻抗的电阻分量，只考虑电抗分量时，则由上式可知三端电流的相位完全相同。在实际运行中，T接输电线路各分支线路的阻抗角相差很小，且△It、△Ib、△Ic有良好的近似同相性，则现在需要考虑实际情况下△It与△Ia的同相性。如果考虑最坏情况下，故障发生A母线出口处，则Zaf=0，此时△It与△Ia之间的相角差也不会超过40°[9]。因此，可知在不考虑分布电容时，△It、△Ia、△Ib、△Ic有良好的同向性。

1.2 外部故障时三端电流关系讨论分析

图3 T接输电线路外部故障时故障分量系统Fig.3 External failure component system of T-connected transmission line

如图3所示，当发生外部故障时，则三端电流△Ia、△Ib、△Ic存在如下关系，式（3）中 Zb∑=Zb+Ztb、Zc∑=Zc+Ztc。

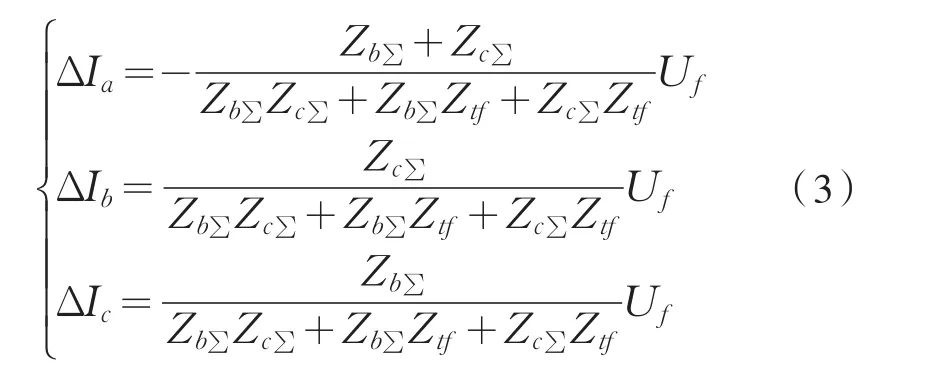
由外部故障时三端电流的表达式知，三端电流的电流相位差异完全取决于相关各阻抗的阻抗角差异。理想情况下，忽略各阻抗的电阻分量，只计电抗分量时，由式（3）可知△Ib、△Ic故障电流方向相同，且与△Ia相反，并且在幅值上存在以下关系：

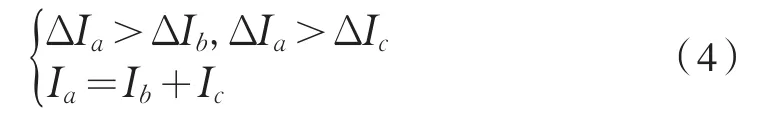
类似于内部故障的分析知不考虑分布电容时，实际输电线路△Ib、△Ic的相差不大，且与△Ia近似相反。

2 三端为电源点T接输电线路故障支路判别方法研究

以下将分别对不同支路发生故障时，流过两电流测量点的电流方向及幅值的变化进行理论推导，分析其变化的规律。

2.1 AT支路发生短路故障

图4 AT支路发生短路故障Fig.4 Short circuit at AT branch

当AT发生单相接地故障时，可得故障发生后工频故障电流方向如图5所示。

图5 AT发生故障后的网络图Fig.5 Thenetwork diagram when fault happens at AT

在T接点，根据基尔霍夫电流定律有，

由于T接输电线路三端故障电流有良好的同向性，则有

2.2 BT支路发生短路故障

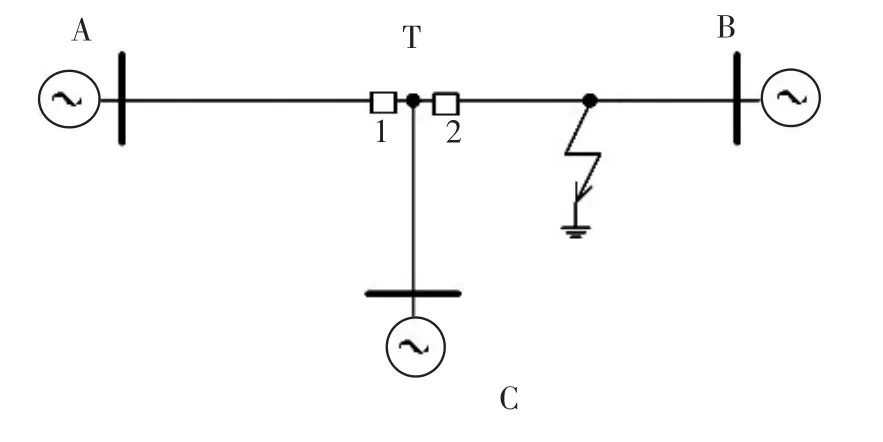
图6 BT支路发生短路故障Fig.6 Short circuit at BT branch

当BT支路发生故障时，工频故障电流网络如图7所示。

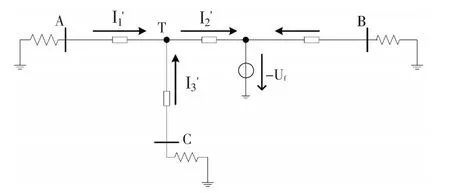
图7 BT发生故障后的网络图Fig.7 Thenetwork diagram when fault happens at AT

与之前讨论的情况类似，在T接点根据KCL定律各支路电流关系如下。

进一步则有：

2.3 CT支路发生短路故障

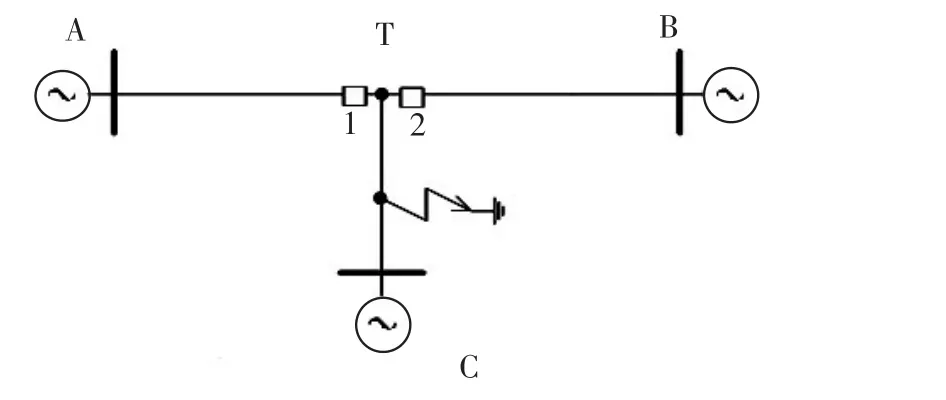
图8 CT支路发生短路故障Fig.8 Short circuit at CT branch

当CT支路发生故障时，工频故障电流网络图如图9所示。

图9 CT发生故障后的网络图Fig.9 Thenetwork diagram when fault happens at CT

此时在3条支路故障电流的关系为=+，但由于设置的电流测量点在AT、BT支路侧，且此时的幅值关系不明确，所以无法利用其幅值作为判据。不过，此时的相位之间则有一定的关系，在理想状态下的相位差刚好是-180°，即反相。

3 一端支路接纯负载的T接输电线路故障支路判别方法研究

以上研究了三端均为电源点的T接输电线路故障支路判断方法，考虑到T接输电线路三端也常会出现一端为负载的情况，而支线负载的引入将会导致故障时短路电流幅值发生变化，为此针对一端支路接纯负载的T接输电线路故障进行研究，探讨其故障前后工频电流幅值、相位关系，提出适用于一端支路纯负载的T接输电线路故障支路判断方法。本文中电流监测点均设为工频电流监测点，可同时监测工频负载电流与工频故障电流。

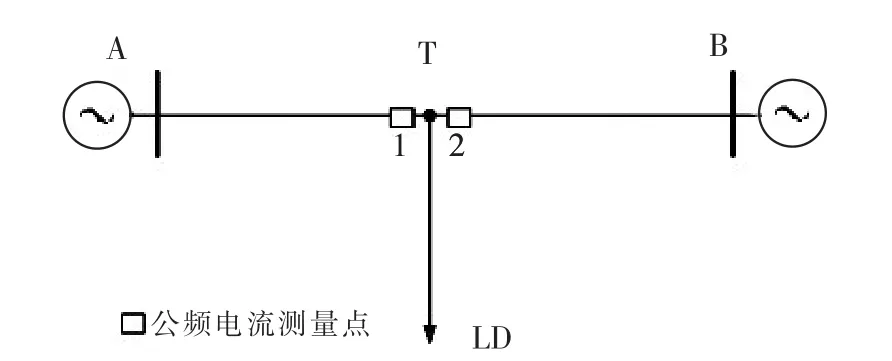
图10 一端支路接纯负载的T接输电线路Fig.10 A T-connected transmission line with a pure load branch

在对一端支路接纯负载的T接输电线路做了大量短路故障仿真计算后发现，仅当CT支路（纯负载支路）发生短路故障时，流过1、2两测量点的工频故障电流还满足较好的反向性。当AT或BT发生短路故障时，1、2两点的工频故障电流幅值间的关系并不明显。因此，需要寻找故障前后新的变量来作为判别故障支路的判定依据。

在此先对一种初始潮流情况进行初步理论分析。当初始潮流方向如图11所示时，若BT分支发生短路故障，则故障后流经1、2测量点的工频电流方向与初始方向相比不会发生改变；而当AT支路发生短路故障时，故障后1、2两测量点的工频电流方向均会发生改变。另外，在线路发生短路故障后，由于故障回路阻抗仅由线路阻抗与接地电阻构成，比线路正常运行时的回路阻抗要小得多，所以在故障持续时间内工频故障电流幅值相较正常时将有大幅升高。

图11 T接输电线路的初始潮流方向Fig.11 The initial power flow direction of T-connected transmission line

经过仿真发现，上述的故障前后工频电流的改变在电流波形图上表现为，故障时刻工频故障电流相位的突变，以及故障后一个周波内幅值的改变。

4 故障点精确定位方法研究

当T接输电线路中某一分支F点发生单相接地故障，输电线路产生的故障初始行波将分别在T接点、故障点、线路对端及T型分支线路对端处产生复杂的折、反射，如图12所示。

图12 故障行波网格示意图Fig.12 Fault travelling wave grid schematic diagram

假设在理想情况下，三条支路的等效波阻抗相等，当行波传输到T节点处时，设Z1为入射波的线路波阻抗；Z2为从入射波方向看进去T接点处的等效波阻抗。行波将要进入的两条支路相当于并联，因此，等效于Z1=2Z2。即折射系数为4/3，因为有两条支路，则进入各条支路的折射波的幅值为入射波的2/3；反射系数为1/3，反射波幅值为入射波的1/3。当行波传输到变电站时，理想情况下可等效为线路装置接电容，根据折反射系数的公式，可知在短时间内，βi=1，发生正的全反射。电容上的电压经过一段时间过渡后，βi变为-1，而行波传播速度非常快，因此，观测到变电站反射波为正的全反射。

线路上发生的故障大多为短路故障。当故障为金属性接地故障时，即行波传输到短路点时，等效于Z2=0，有βi=1，电流行波发生正的全反射。在故障点没有折射波，只有反射波。但实际情况下，故障为非金属性接地时，接地电阻较为明显，故障电流行波在故障点将发生折射和反射。

如上文所述，行波采集监测装置安装于BT支路靠近T接点的位置，可知当故障点位于发生AT与CT支路时，行波折反射规律相似，因而监测点采集行波特征也相似。因此本节仅分析故障点位于AT支路时的情况。

4.1 监测电流行波特征分析

假设AT支路发生故障，监测装置安装在BT支路靠近T接点的位置，则故障点发出行波发出的折反射示意图如图13所示。

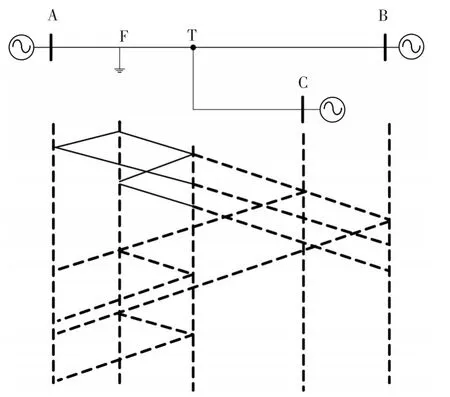
图13 AT支路故障网格示意图Fig.13 Diagram of AT branch fault grid

考虑到T接输电线路行波折反射复杂原因，加之行波传播过程的衰减，尽可能考虑监测点采集电流行波中到达时间最早几个波，因此本文中仅考虑从故障点发出的可能会经过最短路径返回监测装置的波。

行波从故障点F出发向右传至T接点到达监测装置，其可能按以下3条最短路径再次回到监测点：

（1）故障点发出波至T接点，然后经T接点反射回AT支线，再经故障点反射回监测装置，该波是主波经在A接点、故障点之间最短路径的反射波。该波与主波的时间差折算成距离正好等于故障点与T接点距离FT的2倍。

（2）故障点发出波至T接点，然后经过T接点折射至BT支线，然后经过B端母线反射回T接点经过监测装置。该波传播过程中于第一次经T接点的折射与B端母线的反射均不会改变其方向，因而该波与主波保持相同极性，该波与主波的时间差折算成距离正好等于B端母线与T接点距离BT的2倍。

（3）故障点发出波至T接点，然后经过T接点折射至CT支线，然后经过C端母线反射回T接点，然后再折射至监测装置。该波传播过程中于第一次T接点的折射与C端母线的反射均不会改变其方向，但是第二次经过T接点的折射会因传播方向发生改变，因而该波与主波极性相反，该波与主波的时间差折算成距离正好等于C端母线与T接点距离CT的2倍。

行波从故障点F出发向右传至B端母线，则其回到监测装置的最短路径如仅有1条，即故障点发出波至A端母线，然后反射回AT支线至监测装置，该波最开始与主波传播方向相反，后续反射没有改变其极性，因而其与主波极性相反，该波与主波的时间折算成距离正好等于故障点与A端母线的距离FA的2倍。

4.2 故障点精确定位算法提取

由上节分析知故障初始行波在线路对端变电站产生的反射波与主波极性相反，同时初始行波到达T接点后折射至CT支路反射回行波与主波极性相反。因此通过第一个出现的与主波极性相反的波，可求出故障点距离A端母线FA的距离，或者T接点与C端母线的距离CT。假设主波时间为t0，该波出现的时间为t1f，则可以总结出T接故障定位第一种方法，通过式（10）可求出距离x1。

若x1不等于CT的长度，则此波头为故障点折射波，x1等于故障点距离T接点的距离FA；若x1等于CT的长度，则此波头为故障初始行波折射入CT支路后折射回监测装置的波，将此波头排除，继续查找第二个与主波反极性的波。

同理，当根据第二波计算出该波来源与T接点的距离x1，应先与CT长度N倍（N=1，2，3…..）进行比较。如果算出来的x1等于N倍CT的长度，则继续查找下一个，直至找到符合条件FA。考虑到实际情况，通常最多查找到第3个与主波反极性的波就能找到该波。

但是这种定位方法，当故障点的位置距A端母线的距离FT正好等于CT的长度N倍（N=1，2，3…..），定位过程中并不知道故障点的折射波与CT分支对端变电站的反射波叠加，这样就无法找到故障点的折射波，从而无法求出FA，在故障点没有反射波的情况下无法求得FT的距离时，将无法定位。

由分析知经T接点折反射至AT、BT支路的再反射回监测装置的波，与主波极性相同。假设主波时间为t0，第一个与主波极性相同的波出现时间为t1s，则先根据单端行波定位法，总结T接输电线路故障定位第二种方法，依据式（11）计算此波头的来源距T节点的距离x2。

若x2不等于BT长度，则此波头为故障点的反射波，x2等于故障点距离T接点的距离FT；若x2等于BT的长度，则此波头为故障初始行波折射入BT支路后反射回监测装置的波，将此波头排除，继续查找第二个与主波同极性的波。

同理，当根据第二波计算出该波来源与T接点的距离x2，应先与BT长度N倍（N=1，2，3…..）进行比较。如果算出来的x2等于N倍BT长度，则继续查找下一个，直至找到符合条件FT。考虑到实际情况，通常最多查找到第3个与主波同极性的波就能找到该波。

但是这种定位方法，当故障点的位置距T节点的距离FT正好等于BT长度N倍（N=1，2，3…..），定位过程中并不知道故障点的反射波与BT分支对端变电站的反射波叠加，这样就根本找不到故障点的反射波，从而无法求得FT，在故障点没有折射波的情况下无法求得FA的距离时，将无法定位。

定位过程中，每次得到定位结果都应与故障支路的长度相比较，若所得的定位结果比相应的故障支路的长度长，则定位结果错误。

5 结语

T接输电线路故障精确定位研究对于电力系统安全运行具有重要意义，为此按照先实现故障支路的判别、再实现故障点的精确定位的思路，开展了T接输电线路故障精确定位的研究。主要工作和结论如下：

（1）研究了T接输电线路三端电流内部、外部故障以及考虑分布电容影响时的三端电流关系；

（2）研究了三端均为电源点和一端支路接纯负载时的T接输电线路故障支路判别方法，并给出了对应的故障支路判别方法；

（3）研究了T接输电线路故障点精确定位方法，基于电流行波特征分析确定了故障点位置的精确计算方法。

[参考文献]（References）

[1] 束洪春,高峰,陈学允,等.T型输电系统故障测距算法研究[J].中国电机工程学报,1998,(06):41-45.SHU Hongchun,GAO Feng,CHEN Xueyun,et al.A study on accurate fault location algorithm of EHV T-con⁃nection to three terminals[J].Proceedings of the CSEE,1998，(06):41-45.

[2] 张媛媛,朱永利,张宁等.基于行波固有频率和VMD的T型输电线路故障定位[J].电测与仪表,2017,54(21):55-60.ZHANGYuanyuan,ZHU Yongli,ZHANG Ning,etal.A fault location method based on traveling wave watural frequencies and VMD for teed-circuits[J].Electrical Measurement and Instrumentation,2017,54(21):55-60.

[3] 黄力.配电网故障定位的简单矩阵算法[J].湖北电力,2005,(05):1-3.HUANG Li.Simplematrixalgorithm fordistribu⁃tion networks fault location[J].Hubei Electric Pow⁃er,2005,(05):1-3.

[4] 李迅,易谆,王恒.10 kV配电系统故障定位研究[J].湖北电力,2011,35(05):26-28.LI Xun,YI Zhun,WANG Heng.Study on fault locat⁃ing for 10 kV distribution system[J].Hubei Electric Power,2011,(05)：26-28.

[5] 高厚磊,安艳秋,江世芳.超高压T接线路高精度故障测距算法研究[J].电力系统自动化,2001,(20):51-54.GAO Houlei,AN Yanqiu,JIANG Shifang.Study on accuratefault location algorithmfor EHV TeedLines[J].Automation of Electric Power Systems,2001,(20):51-54.

[6] MS Sachdey,R Agarwal.A technique for estimating transmission line fault locations from digital imped⁃ance relay measurements[J].PowerDeliveryIEEE Transactions On,1988,3(1):121-129.

[7] 徐俊明,汪芳宗,夏沛,等.一种无需线路参数的输电线路故障定位算法[J].电测与仪表,2011,48(05):18-21,40.XU Junming,WANG Fangzong,XIA Pei,etal.A fault location algorithm for transmission lines with⁃out line parameters[J].Electrical Measurement and Instrumentation,2011，(05):18-21.

[8] 张利,张峰,梁军,等.带T型分支输电线路的单端行波故障测距[J].电力自动化设备,2010,30(04):46-50.ZHANG Li,ZHANG Feng,LIANG Jun,et al.Fault lo⁃cating based on single-end traveling wavesfor T-type transmission lines[J].Electric PowerAuto⁃mation Equipment,2010(04):46-50.

[9] SH Kang，SJ Lee，YJ Kwon，et al.Transmissionline with a teed circuit[J].PowerEngineering Society Summer Meeting,2001,（2）:921-926.