改进的大型场馆看台区行人疏散时间模型

潘应久 陈淑燕

(东南大学交通学院, 南京 210096)

改进的大型场馆看台区行人疏散时间模型

潘应久 陈淑燕

(东南大学交通学院, 南京 210096)

为改进传统Togawa行人疏散模型无法描述行人动态疏散特性的不足,在行人疏散动态交通特性分析的基础上,基于迭代思想和离散计算方法对传统Togawa模型进行改进,建立了改进的看台区行人疏散时间模型．以陕西省体育场大型活动为例,在行人交通特性分析的基础上,运用改进的疏散时间模型计算看台区行人疏散时间,并将改进的疏散时间模型、传统Togawa模型、Vissim行人疏散模型的仿真结果与实际计算结果进行对比分析．结果表明:改进的疏散时间模型的计算结果与实际调查结果的相对误差为4.4%,精确度最高;同时,改进的疏散时间模型充分考虑了行人疏散过程中的交通流特性,得到的疏散人数随疏散时间变化关系曲线更接近实际疏散过程．因此改进的行人疏散时间模型可以应用于大型体育场馆看台区行人疏散时间的计算．

交通安全;大型场馆;行人交通特性;疏散时间

近几年体育赛事、演唱会等大型活动的举办日益增加,行人的集聚与疏散在一定程度上影响行人的交通安全,当大型体育场馆行人密度过大时,若组织和管理不合理,易造成踩踏等安全事故,而一旦发生安全事故,保证看台区行人流及时有效的疏散至安全区域至关重要．对于行人安全疏散的研究问题,国内外已有一些研究．在建筑物的行人安全疏散时间方面,Togawa[1]针对火灾疏散过程建立了Togawa行人疏散模型. Guo等[2]考虑了高密度聚集环境下行人之间的相互关系,利用元胞自动机建立了行人疏散仿真模型,在此基础上,Guo等[3]考虑了行人疏散过程中不同可见度对疏散路径选择的影响,对行人路径选择进行了研究. 此外,文献[4-8]对行人疏散过程进行了统计分析与模型建立,但忽略了行人交通特性随时间的变化,无法精确反映行人流疏散过程中的动态特性．针对不足之处,张青松等[9]在研究传统疏散计算模型的基础上,提出了改进的疏散模型,验证结果较好,但其离散时间间隔的选取和模型的建立过程依赖于具体的疏散结构,不具备普遍性．

在大型枢纽及大型活动的整体疏散时间方面,周继彪[10]以西安市北大街地铁换乘枢纽为研究对象,建立了基于西安市北大街换乘枢纽站的整体疏散时间模型,并通过实测数据对所建立的模型进行了验证．李俊[11]将大型活动的疏散通道按结构进行划分,分别建立了疏散时间模型,并根据串联及并联特点得到整体疏散时间模型,但并没有对场馆看台区进行疏散时间研究．纪英[12]针对大型活动提出了行人交通需求预测方法,从时间和空间角度对行人交通需求的分布特性进行了分析,并提出有效的行人流组织和管理方案．

为精确反映行人交通特性对疏散过程的影响,本文首先对Togawa模型的推导过程进行分析,针对Togawa模型存在的不足进行改进,充分考虑了疏散过程的人群流动系数随时间的变化特性,建立了改进的看台区行人疏散时间模型．

1 传统Togawa模型

在行人疏散研究中,考虑到建筑物不同出口的行人流量差异及不同出口的宽度对疏散的影响,Togawa[1]提出了计算建筑物疏散过程的疏散时间模型．模型的推导过程如下．

设建筑物内有n个通往安全出口的分出口,第i条通道的单位流率为fi(t),宽度为Bi．则从疏散开始到时间T内,从各分出口到达最终安全出口的总人数为

(1)

随着疏散过程的进行,汇集到安全出口的待疏散人数不断增加．当达到人数大于安全出口最大可疏散人数时,安全出口的待疏散行人发生滞留．假设发生滞留的时刻为T0,取0→T0时间段内汇集到安全出口的人数为yf,T0→T时间段内汇集到安全出口的人数为yc,安全出口的单位流率为f,宽度为B,则有

yc=(T-T0)fB

(2)

那么,0→T时间段内从安全出口安全通过的人数yout为

yout= yf+yc=

(3)

设滞留人数为yz,则有

(4)

(5)

即

(6)

在整个行人疏散过程中,由于无法确定行人发生滞留的具体时刻,即T0无法求得,故式(6)无法求解．针对这一问题,Togawa对模型进行了简化,得到如下方便计算的经验公式:

(7)

式中,Na为待疏散总人数;L为距离安全出口最长距离;V为行人自由行走的速度．式(7)就是传统Togawa模型,该模型计算简便,适合工程计算,但是忽略了行人在各疏散通道的动态交通特性,用L/V简单表示T0无法精确描述行人疏散的动态变化过程．

2 改进的行人疏散时间模型

针对传统Togawa模型无法描述行人动态疏散特性的不足,本文结合Togawa模型的推导过程,从离散时间和迭代计算的角度对传统Togawa模型进行改进．

用t(n)表示行人的疏散时刻,则在疏散时间0→t(n)内,t(n)时刻各疏散通道疏散到猫洞出口(安全出口)的人数为

(8)

在第i个疏散通道的离散时间间隔Δti内,第i个疏散通道截面通过的行人数量为

ni=Δtiqi

(9)

则m个通道通过的行人总数为

(10)

利用迭代思想,可得t(n)与t(n-1)时刻到达猫洞出口的人数关系为

(11)

T0时刻后,猫洞出口疏散总人数可表示为

(12)

基于迭代思想,式(12)可以作如下转换:

(13)

由式(11)和(13)可以得到t(n)时刻的滞留人数为

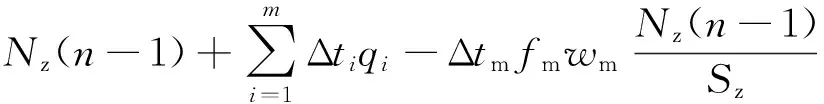
(14)

从而得到T0→t(n)时刻的疏散人数为

(15)

式中,Nz(n)为t(n)时刻滞留猫洞的人数;Ns(n)为t(n)时刻从猫洞疏散的人数;Wi为第i条通道的宽度;wm为猫洞通道宽度;Δtm为猫洞的离散时间间隔;Sz为滞留区面积;fi为第i个楼梯通道的人群流动系数;fm为猫洞通道人群流动系数;qi为第i条通道的截面流量.

模型参数的确定方法如下:

① 猫洞出口的人群流动系数fm．fm并非定值,随疏散过程的不断进行,以及猫洞通道行人流量的不断变化,人群流动系数也随之变化．张青松等[9]通过对人群流动系数与密度的经验关系分析表明,人群流动系数不同的取值对模型结果有不同的影响．因此,为更精确地反映人群流动系数的变化特性,本文通过对调查数据拟合,得到行人流量随疏散时间的变化关系,进而得到人群流动系数随疏散时间的变化关系为

(16)

式中,Fm(t)为猫洞通道处行人流量随时间变化的函数．

② 确定离散时间间隔．各通道的离散时间间隔表示单股行人流从通道走出的平均间隔时间,即

(17)

Δt=max(Δt1,Δt2,…,Δti,…)

(18)

则疏散时间可表示为

t=nΔt n=1,2,3,…

(19)

③ 其他参数可根据疏散结构的物理尺寸确定．

3 模型验证

3.1 体育场看台区的选取

陕西省体育场的观众席划分为20个看台区,各看台区间设有隔离栏,相互独立,体育场共可容纳观众50 100人．为方便观众的疏散,体育场共配设42个猫洞出口,每个看台区设有2个猫洞,每个猫洞出口宽度为2m．研究中以体育场29#，30#猫洞所在的看台区为例,对改进的行人疏散模型进行应用．29#，30#猫洞结构示意图如图1所示,猫洞结构及通往猫洞的楼梯通道名称见图1(a)．

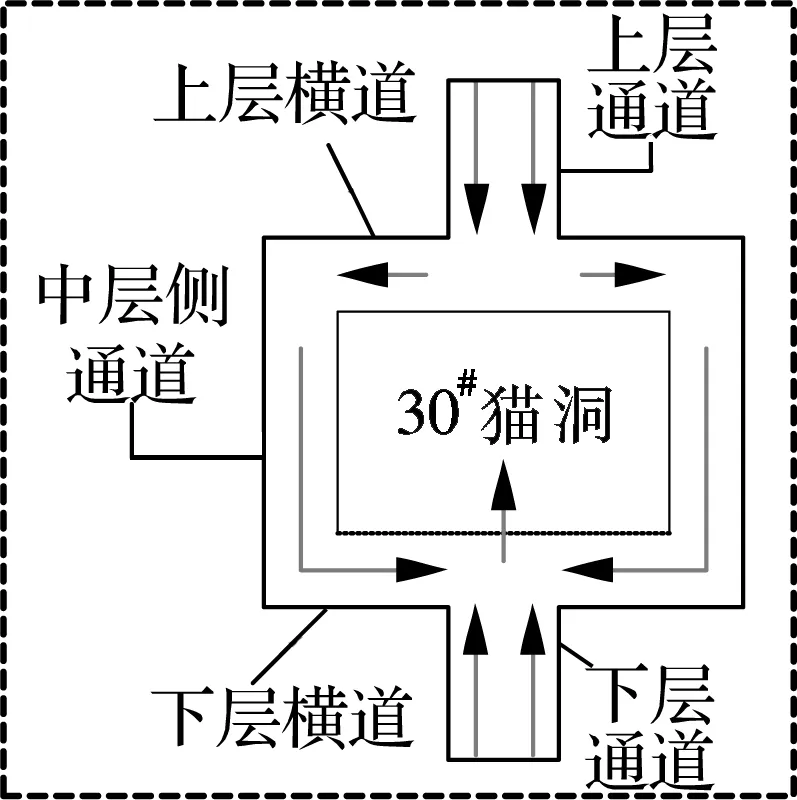
(a) 猫洞结构放大图

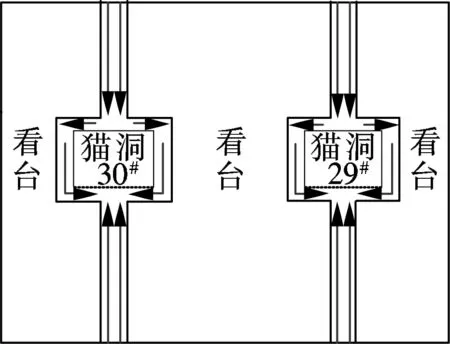
(b) 看台区示意图

该区域共32排座位,共有1 728个座位．该看台区的座位被楼梯通道划分为3个部分,从左到右的座位数分别为480,800,448．中间区域的800个座位上的行人在散场疏散过程中,可以自由选择任意2个猫洞出场．但考虑到行人的最短路径及最短时间的选择特性,理想地认为以中线为分隔线,左侧的400个座位观众从30#猫洞出场,右侧的400个座位观众从29#猫洞出场．即认为在观众坐满的情况下,29#，30#猫洞待疏散行人的总人数分别为848,880．因此研究中只以待疏散人数较大的30#猫洞为例．

通过现场调查,观众席各类型通道的物理尺寸如表1所示．

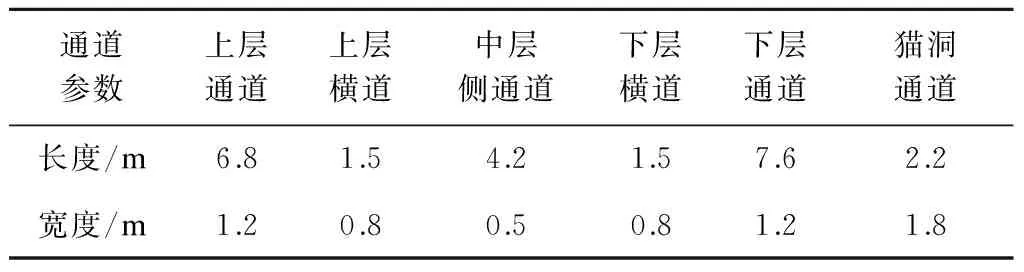
表1 观众席各类型通道的物理尺寸

3.2 数据采集与交通特性分析

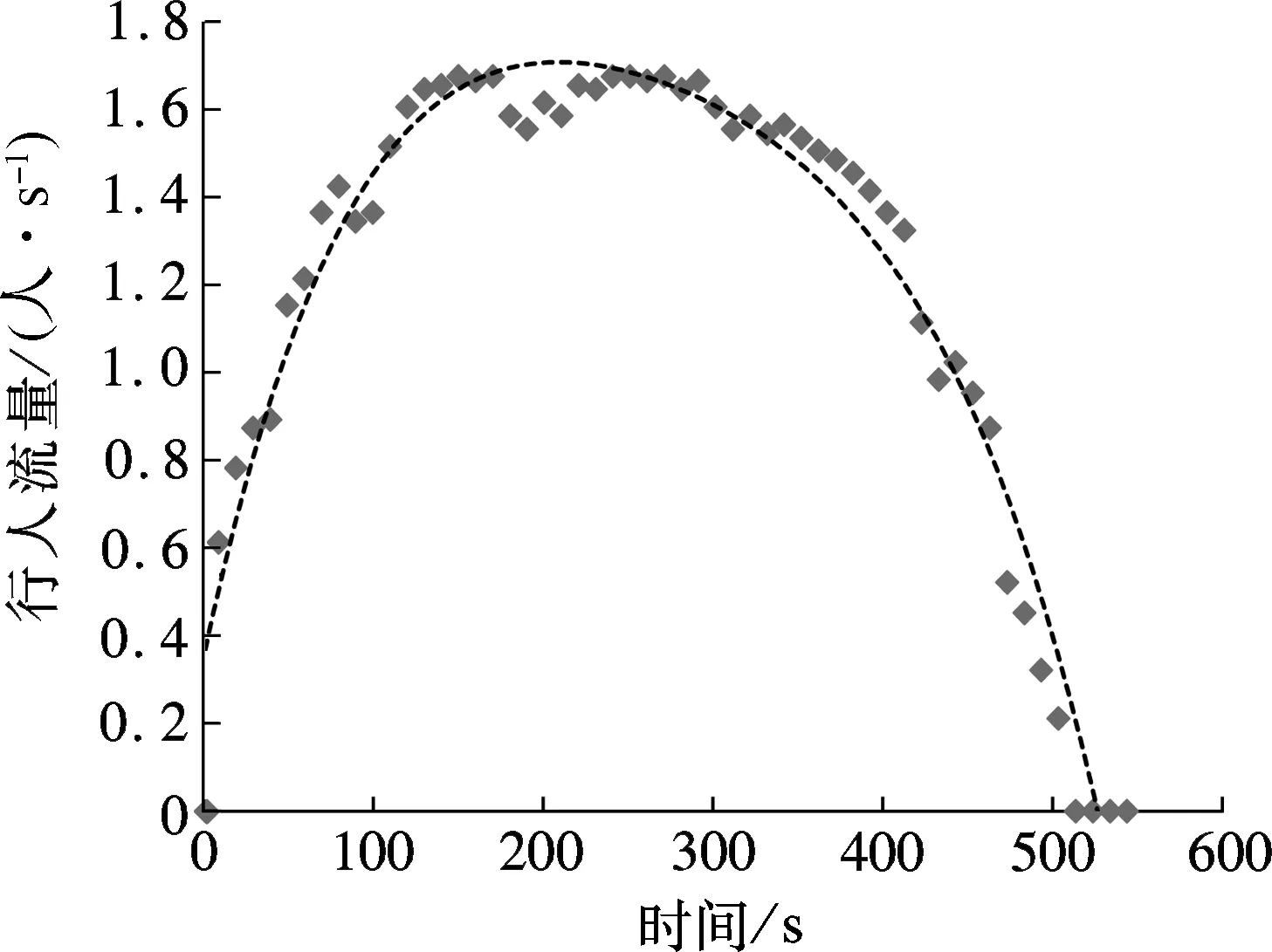
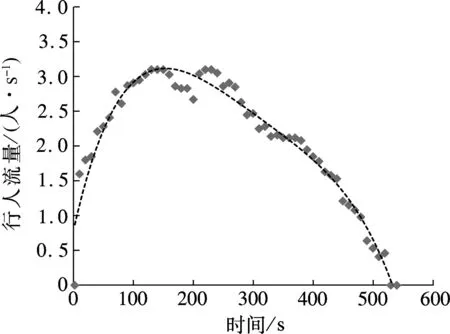
对2016年3月28日举办的中国对阵卡塔尔的体育赛事活动进行现场调查,采用视频数据采集方法,对29#，30#猫洞所在的看台区行人疏散过程进行了数据采集,通过处理调查数据,并进行曲线拟合,得到了上层通道、下层通道和猫洞通道截面行人流量随疏散时间的变化关系,如图2所示．

分别对上层通道、下层通道和猫洞通道得到的流量数据进行拟合,得到如下函数关系：

1) 上层通道处的行人流量随时间变化的函数关系为

2.217×10-7x3-2.147×10-10x4

(20)

2) 下层通道处的行人流量随时间变化的函数关系为

1.889×10-7x3-1.717×10-10x4

(21)

3) 猫洞通道处的行人流量随时间变化的函数关系为

A 使用自动白平衡可以相对简单直观，但精确来讲，不适合所有拍摄条件。手动调节白平衡可以使不同拍摄条件下的色温保持更加精确。我的建议是，当你没有时间手动精确设置白平衡时可以选择折衷方案。不用相机的自动白平衡设置，而是从相机提供的白平衡预设入手。通常大多数相机都会提供不同的白平衡预设选择，如日光、阴天、阴影、钨丝灯/白炽灯、荧光灯与闪光灯。通过选择与照明情况相符的预设，就能得到与当前场景接近的精确的白平衡设置，无需在后期处理时进行调整。

4.610×10-7x3-3.675×10-10x4

(22)

由各通道结构的拟合函数发现,随着疏散时间的改变,观众席上层通道、下层通道和猫洞通道结构的行人流量变化与疏散时间呈四次函数关系．曲线拟合的决定系数R2值分别为0.944,0.956和0.945,可知曲线拟合程度均较好．

(a) 上层通道

(b) 下层通道

(c) 猫洞通道

3.3 模型计算与对比分析

根据对看台区的实际调查数据,分别确定各模型参数．

1) 各通道的行人流股数ci．根据调查,上层通道截面行人流股数c1=2;下层通道截面行人流股数c2=2;猫洞洞口的行人流股数cm=4．

2) 猫洞洞口的人群流动系数fm．由表1可得猫洞宽度为1.8 m,结合式(22)得到人群流动系数函数为

4.610×10-7x3-3.675×10-10x4)

(23)

因此,根据式(18)确定模型的离散疏散时间Δt=1.90s,根据式(19)得到模型的疏散时间为t=Δtn=1.90n(n=1,2,3,…)．30#猫洞待疏散的行人容量为880人,将各参数值代入模型(15),利用Matlab软件对模型编程求解,得出总疏散时间为450s．

采用Vissim6.0中的行人模块,对30#猫洞所在的看台进行仿真,并利用实际调查数据对行人模块中的参数进行标定．仿真过程如图3所示．

(a) 10 s

(b) 50 s

(c) 100 s

(d) 150 s

(e) 200 s

(f) 250 s

(f) 300 s

(h) 350 s

(i) 400 s

(j) 450 s

将改进疏散时间模型、传统Togawa模型、Vissim仿真结果与实际调查的疏散结果进行对比分析,以验证模型求解结果的合理性．

Vissim仿真结果、传统Togawa模型的计算结果、改进模型计算结果及实际调查结果的疏散人数随疏散时间变化曲线如图4所示．其中，传统Togawa模型计算时,f取1.33人/(m·s),V取0.9 m/s．

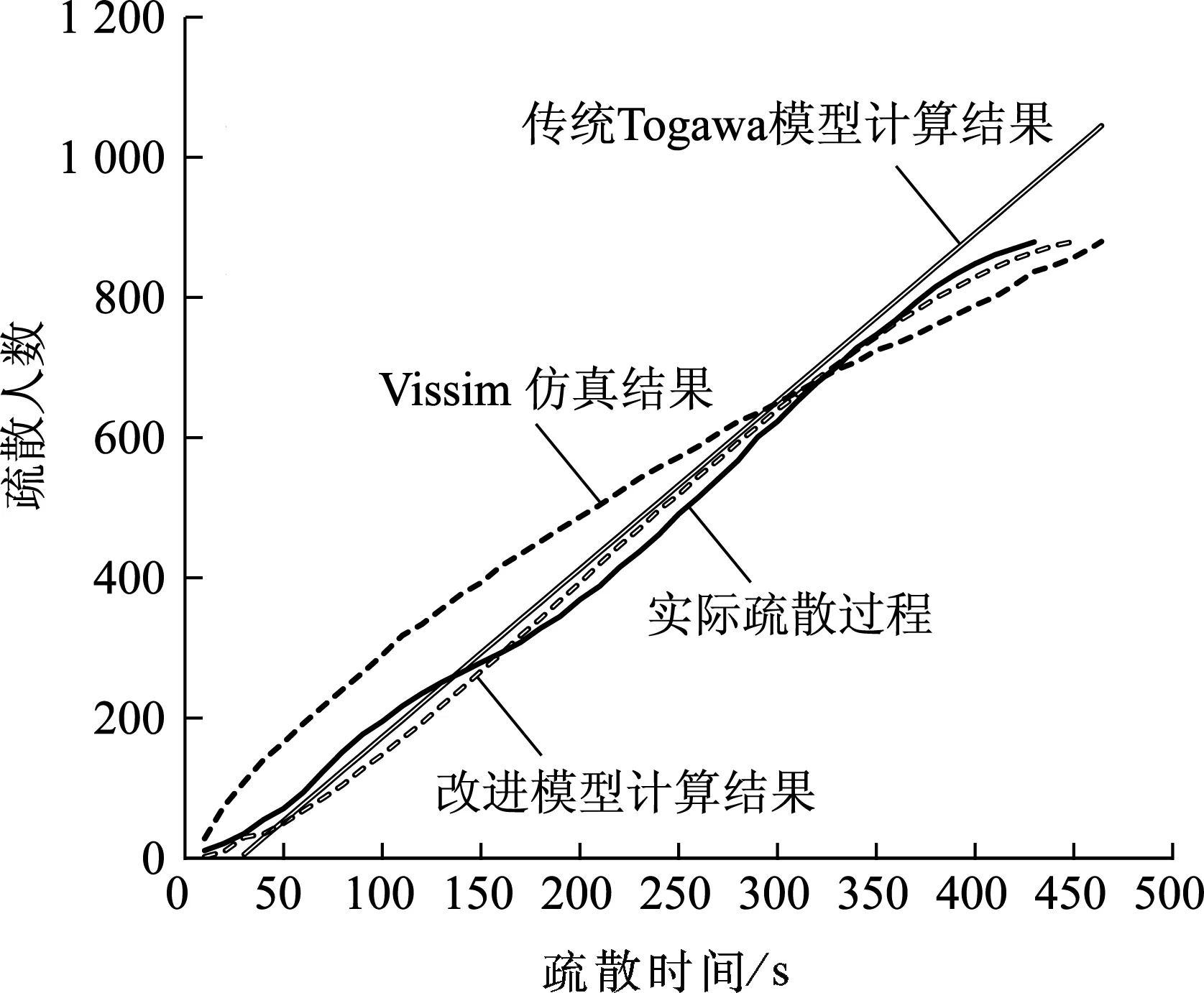
图4 不同方法下疏散人数与疏散时间关系曲线

Vissim仿真结果、传统Togawa模型计算结果、改进模型计算结果与实际调查结果的相对误差如表2所示．

表2 疏散时间计算结果及相对误差

由表2可知,Vissim仿真结果与实际调查结果的相对误差为7.7%;传统Togawa模型计算结果与实际调查结果的相对误差为8.4%;本文改进模型计算结果与实际调查结果的相对误差仅为4.4%,结合图4中模型计算与调查结果的对比曲线,可得出如下分析结论:

1) 传统Togawa模型计算结果与实际调查结果对比.传统Togawa模型的各参数取值均为经验值,计算结果仅与距离安全出口的最长距离L和猫洞的有效宽度B有关,并且疏散人数与疏散时间呈线性关系,这与实际情况不相符,求解结果与实际调查结果的相对误差也较大．

2) Vissim仿真结果与实际调查结果对比.疏散初始时刻,Vissim仿真软件忽略了行人从座位起身的缓冲时间,只是以参数设置的行人速度区间进行疏散过程仿真,因此初始时刻疏散曲线斜率较大;随着疏散过程的进行,疏散曲线斜率逐渐趋于稳定;疏散过程的尾声,疏散人数逐渐减少,疏散曲线斜率变小,直至疏散结束．Vissim仿真与实际疏散过程除在初始时刻误差较大外,其余时刻误差较小,总体相对误差为7.7%．

3) 改进的疏散时间模型计算结果与实际调查结果对比.利用改进的疏散时间模型计算得到的疏散曲线与实际调查疏散曲线总体较接近,相对误差仅为4.4%,精确度较高,与其他计算方法相比更符合实际疏散情况．只是在疏散的初始时刻,存在一定误差,改进疏散模型的斜率在疏散初始阶段较小,这是因为在疏散初始阶段,观众需要从座位起身,沿疏散通道走向猫洞,从观众起身到第一位观众到达猫洞,这段时间的疏散人数为0,导致疏散初始阶段斜率较小;随着疏散时间的增加,斜率增大并趋于稳定,这是因为随着疏散过程的进行,疏散流逐渐趋于稳定;在疏散时间的后半段,疏散斜率逐渐下降并趋于平缓,这是因为随着疏散时间的增加,待疏散的行人总数不断减少,虽然行人的平均步行速度和行人流量有所增加,但疏散率有所下降,最后疏散完毕．但由于模型忽略了T0时刻的疏散人数,因此与实际调查结果曲线在初始疏散时刻有一定差异,这也是今后需继续深入研究的方向．

4 结论

1) 传统Togawa疏散模型是一个简化模型,其人群流动系数取经验数值,忽略了行人在各疏散通道的交通特性．本文提出的改进模型既考虑不同通道的行人交通特性,又考虑了人群流动系数随疏散时间的变化关系,更加符合实际的疏散情况．

2) 改进的疏散时间模型没有直接给出疏散时间的表达式,而是给出了疏散人数与离散时间的迭代关系表达式,通过Matlab编程求解可得到不同离散时刻的疏散人数,同时还可得到不同时刻猫洞出口的滞留人数．分别利用改进的疏散时间模型、传统Togawa模型及Vissim行人疏散模块进行计算,并与实际调查结果对比可知:在疏散时间计算结果方面,与实际调查结果相比,改进的疏散时间模型的相对误差要小于传统Togawa模型和Vissim仿真结果的相对误差,精确度最高;在疏散过程方面,改进的疏散时间模型充分考虑了行人疏散过程的交通流特性,比传统Togawa模型及Vissim仿真过程更加符合实际情况,可以应用于大型体育场馆看台区行人疏散时间的计算,并为体育场看台区的疏散通道规划与设计提供理论依据．

References)

[1]Togawa K. Study on fire escapes basing on the observation of multitude currents[R]. Tokyo, Japan: Building Research Institute, Ministry of Construction, 1955.

[2]Guo R Y, Huang H J. A modified floor field cellular automata model for pedestrian evacuation simulation[J].JournalofPhysicsA:MathematicalandTheoretical, 2008, 41(38): 385104. DOI:10.1088/1751-8113/41/38/385104.

[3]Guo R Y, Huang H J, Wong S C. Route choice in pedestrian evacuation under conditions of good and zero visibility: Experimental and simulation results[J].TransportationResearchPartB:Methodological, 2012, 46(6): 669-686. DOI:10.1016/j.trb.2012.01.002.

[4]Zhao H, Gao Z. Reserve capacity and exit choosing in pedestrian evacuation dynamics[J].JournalofPhysicsA:MathematicalandTheoretical, 2010, 43(10): 105001. DOI:10.1088/1751-8113/43/10/105001.

[5]Zhang L, Liu M, Wu X, et al. Simulation-based route planning for pedestrian evacuation in metro stations: A case study[J].AutomationinConstruction, 2016, 71: 430-442. DOI:10.1016/j.autcon.2016.08.031.

[6]von Krêchten C, Schadschneider A. Empirical study on social groups in pedestrian evacuation dynamics[J].PhysicaA, 2017, 475: 129-141.

[7]Kunwar B, Simini F, Johansson A. Evacuation time estimate for total pedestrian evacuation using a queuing network model and volunteered geographic information[J].PhysRevE, 2016, 93(3): 032311. DOI:10.1103/PhysRevE.93.032311.

[8]Huo F, Song W, Chen L, et al. Experimental study on characteristics of pedestrian evacuation on stairs in a high-rise building[J].SafetyScience, 2016, 86: 165-173. DOI:10.1016/j.ssci.2016.02.025.

[9]张青松, 刘茂, 赵国敏. 改进的疏散时间计算模型在奥运赛场中的应用[J].中国工程科学, 2007,9 (4): 64-69. DOI:10.3969/j.issn.1009-1742.2007.04.012. Zhang Qingsong, Liu Mao, Zhao Guomin. A modification of evacuation time computational model and simulation comparison analyses with olympic stadium[J].EngineeringScience, 2007,9(4): 64-69. DOI:10.3969/j.issn.1009-1742.2007.04.012. (in Chinese)

[10]周继彪. 综合交通换乘枢纽行人交通特性及安全疏散研究[D]. 西安: 长安大学公路学院, 2014.

[11]李俊. 行人交通疏散模型研究[D]. 广州:华南理工大学土木与交通学院, 2011.

[12]纪英. 大型活动行人交通组织与管理方法研究[D]. 长春:吉林大学交通学院, 2007.

Improved model about pedestrian evacuation time in large-scale stadium audience area

Pan Yingjiu Chen Shuyan

(School of Transportation, Southeast University, Nanjing 210096, China)

The shortcomings of the traditional Togawa model were found through the analysis of the derivation process. Under the dynamic traffic characteristics analysis of pedestrian evacuation, the evacuation time model in the audience area was established based on the iteration theory and discrete computational methods. The improved evacuation time model was applied to the audience area of the stadium in Shaanxi Province and the evacuation time was analyzed based on the characteristics of the pedestrian transportation. The evacuation time calculated by the improved model, the traditional Togawa model and the Vissim simulation were compared with the practical survey results, respectively. The calculation results show that the relative error between the calculated results of the improved evacuation time model and the practical survey results is 4.4%, it has the highest accuracy in terms of evacuation time, and in the evacuation process, the evacuation curve obtained by the model is more reasonable than those obtained by Vissim simulation and traditional Togawa model. Based on the results, the improved model can be used for the calculation of pedestrian evacuation time in large-scale stadium audience area.

traffic safety; large-scale stadium; pedestrian traffic characteristics; evacuation time

10.3969/j.issn.1001-0505.2017.03.032

2016-10-10. 作者简介: 潘应久(1990—),男,博士生;陈淑燕(联系人),女,博士,教授,博士生导师, chenshuyan@seu.edu.cn.

国家自然科学基金面上资助项目(61374195)．

潘应久,陈淑燕.改进的大型场馆看台区行人疏散时间模型[J].东南大学学报(自然科学版),2017,47(3):613-618.

10.3969/j.issn.1001-0505.2017.03.032.

U491

A

1001-0505(2017)03-0613-06