高中学生数学思维障碍成因及其突破

于杭君

摘要：新课程改革要求中学培养学生要注意培养学生的数学核心素养，其中便包含了数学思维能力的培养。但是，目前高中生经常会反应自己对数学学习缺乏兴趣，有些题听懂但不会做，从而失去信心，造成数学思维能力的障碍。当然，学生自身基础知识薄弱，学习方法的不恰当或者说教师的不恰当教学方法，都可能使学生产生数学思维障碍。这就造成了学生成绩下降明显，感觉自己无法适应高中数学的学习。本文就从高中学生数学思维障碍的成因分析，从而突破数学思维障碍。

关键词：数学思维障碍；成因；对策

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2017）04-0022

所谓数学思维，就是以数学问题为载体，通过发现问题、解决问题的形式，达到对现实世界的空间形式和数量关系的本质的一般性认识的思维过程。高中生在学习数学的过程中，其数学思维就是对数学知识通过分析比较、归纳联系等思维方式来理解并掌握其内在的本质和规律。高中生在学习数学时，发现自己并非是自己不努力，上课也能听懂，但是下课作业却很难独立完成，这便是学生对于课堂教学存在数学思维障碍的问题。因此，如果不能及时解决会对学生学习数学产生较大的影响，所以在教学过程中要注意学生学习数学的思维障碍问题。如果引起重视，可以让学生学习数学得到事半功倍的效果。

一、高中学生数学思维障碍存在的原因

1. 学生非智力因素的影响

笔者做过一次问卷调查，由于数学本身有着较强的严谨性和逻辑性，课堂氛围比较严谨，对于部分学生来说是有些枯燥，再加上有些学生自身比较懒惰，既怕苦又怕累，觉得学习数学很苦很累并且很乏味，是逼不得已而为之的事情，所以大部分学生对学习数学的兴趣不高，也缺乏学好的自信。特别是初升高后，高中课堂容量增大，有些学生在几次考试后成绩相比于初中下滑很大，对学生的自信心打击很大，因此产生了对学习数学没有自信的现象。而且有较大部分学生对于课堂中一知半解的题目不求甚解，遇到稍微难一点的题目就不能静下心来思考，也不敢下手，学习数学的意志力薄弱。长久以往，養成了思维的惰性，进而产生了学习数学思维障碍的情况。

2. 学生原有的数学基础知识不牢固

根据布鲁纳的认识发展理论，学习本身是一种认识过程，在这个过程中，个体的学习总是要通过已知的内部认知结构，对“从外到内”的输入信息进行整理加工，以一种易于掌握的形式加以储存。当新的知识与学生原有的知识结构不相符时或者新旧知识中间缺乏必要的“媒介点”时，这些新知识就会被排斥或经“校正”后吸收。有些学生原有的知识不牢固，导致在学习新知识的时候，衔接不上，不能将新旧知识加以整合，成为解决问题的障碍。

3. 学生不正确的思维习惯的影响

高中学生通过初中学习已经具有相当丰富的思考与答题经验，所以有一些学生思维定势，缺少根据新的问题的特点，运用已学的知识，作出灵活的反应，经常阻抑更合理、更有效的思维，甚至造成歪曲的认识。

对于高中数学概念或原理的学习，学生很少会对其产生、发展过程进行深刻理解。比如等差数列的教学，多数学生仅仅只是对于公式记忆，但对于公式的推导过程并不在意，所以当出现累加法时便成为不会的问题。另一方面，学生懒于思考，对观察得到的关键信息感知较少，思维不连贯，想到这点忘了那点，缺少知识的横向比较。例如等差和等比数列的题目，一道题目既有等差数列又有等比数列，部分学生就难以将题目条件加工成有价值的条件信息，从而造成思维受阻。

4. 教师的不恰当教学方式方法使学生数学思维障碍

笔者的问卷调查结果显示，学生对于教师所设计的激发学生学习兴趣的问题情境，只有极小部分学生认为真正地激发了他们的学习热情。由于高中数学知识含量大，教学任务重，部分教师会因此上课赶进度，对知识的形成过程讲解不到位，概念模糊不清，平时练习采用题海战术，使教学与学生的基础与接受水平不协调，从而造成了学生数学思维障碍。

二、打破高中生数学思维障碍的对策

1. 培养学生良好的思维习惯

我们可以通过设计“一题多解”“一题多变”进行训练，既拓宽思路，又增强知识间联系，使学生学会从多角度去思考解题的方法和形成灵活的思维方式。在教学过程中，用多种方法，从各个不同途径、不同角度寻求答案，培养学生思维过程的灵活性。例如：

求证：■=tanθ

证法1：（运用二倍角公式统一角度）

左=■=■=右

证法2：（逆用半角公式统一角度）

左=■=■=右

证法3：（运用万能公式统一函数种类）设tanθ=t

左=■=■=t=右

证明4：（构造分母sin2θ并使分子进行重新组合，从而在运算形式上得到统一。）

∵tanθ=■

∴左=■=■=右

证法5：变更论证法。即证：

（1-cos2θ+sin2θ）sin2θ=（1-cos2θ）（1+cos2θ+sin2θ）

一题多解引导学生头脑风暴，把三角函数的知识点练习比较，既能使学生加深知识运用和内在练习的理解，降低思维定势。

教师在教学过程中不能满足证明的定理、公式，更应该注重数学思维过程的分析，让学生注意证明思路的由来。 （上接第22页）在解答的过程中尽量仔细讲解自己的思维形成过程，多用变式迁移，慢慢地让学生形成自己的数学思维，让学生了解数学逻辑的严密性和概括性以及数学思维的抽象性和符号化的特点。

注意培养学生的归纳、反思的能力。在教学过程中注重总结归纳答题的规律，引导学生对于题目答题思路的反思，对不同题目思路中的共同点进行比较。同时，注意引导学生对知识的整理，形成系统的知识体系，帮助学生架构系统的知识框架。

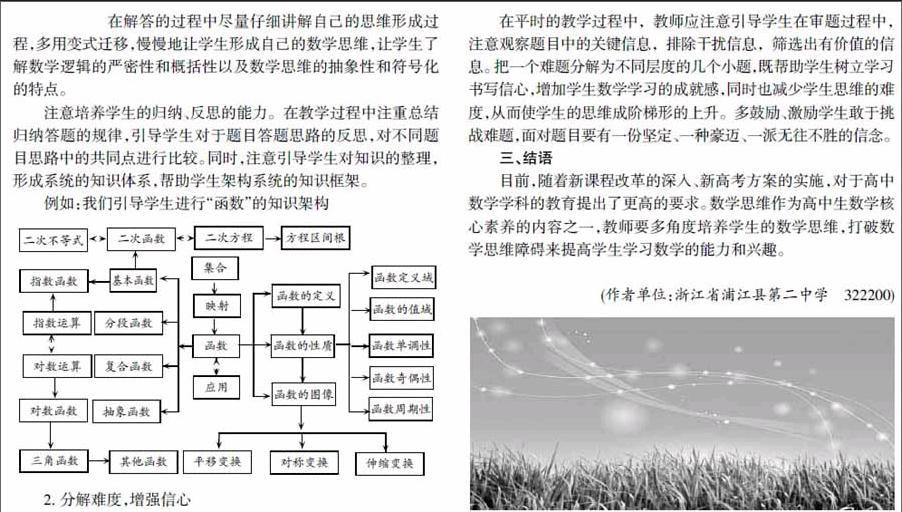
例如：我们引导学生进行“函数”的知识架构

2. 分解难度，增强信心

在平时的教学过程中，教师应注意引导学生在审题过程中，注意观察题目中的关键信息，排除干扰信息，筛选出有价值的信息。把一个难题分解为不同层度的几个小题，既帮助学生树立学习书写信心，增加学生数学学习的成就感，同时也减少学生思维的难度，从而使学生的思维成阶梯形的上升。多鼓励、激励学生敢于挑战难题，面对题目要有一份坚定、一种豪迈、一派无往不胜的信念。

三、结语

目前，随着新课程改革的深入、新高考方案的实施，对于高中数学学科的教育提出了更高的要求。数学思维作为高中生数学核心素养的内容之一，教师要多角度培养学生的数学思维，打破数学思维障碍来提高学生学习数学的能力和兴趣。

（作者单位：浙江省浦江县第二中学 322200）