基于模拟退火机制的人工蜂群算法的结构损伤识别*

周梓檀, 刘济科，吕中荣，丁政豪

(中山大学工学院，广东 广州 510275)

基于模拟退火机制的人工蜂群算法的结构损伤识别*

周梓檀, 刘济科，吕中荣，丁政豪

(中山大学工学院，广东 广州 510275)

人工蜂群算法是模仿蜜蜂行为提出的一种群智能优化算法。 它的主要特点是只需要对问题的解进行优劣的比较，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，具有较快的收敛速度，但较容易陷入局部最优解。为了克服这一不足，将模拟退火算法机制引入其中进行改进。既保留了蜂群算法群体寻优的特点，又可以有效地避免陷入局部最优解。通过选择合适的收益率函数和温度下降函数，可以很方便地解决优化问题。通过构造基于残余力向量的损伤识别目标函数，利用改进的人工蜂群算法，能有效地解决结构损伤识别问题。通过对桁架模型进行数值模拟，结果表明文中算法就原算法而言，收敛速度，识别精度和抗噪声能力有较好改善。

人工蜂群算法；模拟退火算法；残余力向量；损伤识别

我国是一个多自然灾害的国家，几乎每年都要发生地震、火灾和风灾等重大的自然灾害，这些自然灾害对土木工程结构的安全造成了严重的威胁。再者，土木工程结构和重大基础设施使用环境恶劣，随着使用时间的增长，由于环境荷载的作用以及疲劳效应和材料老化等诸多因素影响，结构不可避免地产生抗力衰减和损伤积累。一旦结构关键构件的损伤累积到了一定的程度，而没有被及时发现和处理，损伤将迅速扩展，从而导致整个结构的破坏，由于未能及时发现结构损伤而造成的悲剧不胜枚举。因此需要对结构的健康状况进行监测，及时发现结构的损伤，同时，如果尽早地发现这些损伤，有利于维护。基于上述原因，结构损伤检测在近几十年来一直是人们关注的重点，国内外众多学者进行了这一方面的研究。结构发生损伤之后，结构的动力特性就会随之改变。早期结构损伤识别主要是研究结构有限元模型动力修正问题，在此基础上，开始了基于振动测试的结构损伤识别的研究，发展了许多方法和理论[1-6]。从计算的角度来看，结构损伤识别问题可以看作优化问题，通过定义一个关于系统模型的目标函数，可以利用优化的手段来实现参数的识别。蜂群算法是一种模拟群体蜜蜂觅食特性的智能优化算法，具有参数设置简单、易于实现的特点[7-11]。本文在原有蜂群算法的基础上结合模拟退火算法，以改善蜂群算法后期易于陷入局部最优的缺点，从而改善搜索精度。残余力向量法由Zimmerman等[12]提出，是一种精度较高的识别方法。本文基于残余力向量建立损伤识别问题的目标函数,利用蜂群算法对该目标函数进行求解,获得损伤的位置和程度。并且和原始算法进行对比，结果表明改进的算法识别精度更高，抗噪能力更强。

1 改进蜂群算法

1.1 人工蜂群算法

在蜜蜂采蜜的过程中，蜜蜂被分为两大类：雇佣蜂和非雇佣蜂。雇佣蜂又称引领蜂，非雇佣蜂又被分为跟随蜂和侦查蜂两大类。引领蜂的任务是寻找食物，并且将找到的食物源以“摇摆舞”的形式传递给非雇佣蜂。“摇摆舞”中包含了食物源所在位置和收益率等众多丰富的信息，这些信息都是通过“摇摆舞”的舞动频率和持续时间体现出来，然后跟随蜂根据相关信息，选择是否跟随和跟随哪只引领蜂，跟随的概率通常与食物收益率成正比，并且它们会在引领蜂食物源附近进行探索，当引领蜂经过若干次探索后，食物源信息都没有得到更新，则该引领蜂成为侦查蜂，侦查蜂的任务是探索新的食物源。在蜂群算法的整个搜索过程，每个食物源代表优化问题的一个可行解，食物源的收益率决定了解的优劣，收益率越高，所得到的解越接近最优解。蜂群算法对食物源的选择概率采用轮盘赌的形式

(1)

其中：s为食物源个数，F为食物源收益率，xi为第i个食物源跟随蜂在选择食物源后，会在其领域内选择一个新食物源xj它的计算公式如下

xj=xi+Δx

(2)

其中Δx表示步长，再比较两个食物源的收益率，选择收益率较大的食物源作为当前食物源。

1.2 引入模拟退火机制的人工蜂群算法

模拟退火算法是来源于固体退火原理，其主要优点在于能够利用高温时粒子的无序性，有效地避免陷入局部最优解[13]。本文将该机制引入人工蜂群算法当中，即当新食物源收益率低于当前食物源时，仍然以一定的概率接受新食物源。模拟退火中退火温度T决定了蜜蜂接受低收益率食物源的概率，温度越高，接受低收益率食物源越大，温度越低则越小，因此在算法迭代初期，退火温度应该较大，进而让算法趋于全局搜索，迭代后期，温度应该越来越小，进而让算法趋于局部重点搜索，加快算法收敛。因此，温度下降函数T(t)选取如下

T(t+1)=σT(t)

(3)

其中：σ为退火系数，取值范围[0.9,1)，当进行收益率比较时，对比新食物源收益率Fn和当前食物收益率Fc，计算它们的差值，

ΔF=Fc-Fn

(4)

当差值小于零时，选择新食物源；当差值大于零时，按照退火规则遴选食物源。

(5)

如果(5)式成立，则接受新食物源，如果不成立，则拒绝新食物源。

2 残余力向量及目标函数

2.1 残余力向量

忽略阻尼的结构运动方程

(6)

相应特征方程为

(K-λjM){Φ}j=0

(7)

式中：K,M,λ,Φ分别为刚度矩阵、质量矩阵、相应的特征值和特征向量。

Kd=Ku-ΔK

(8)

结构发生损伤时

(Kd-λdjMd){Φ}dj=0

(9)

相应的第j阶残余力为

Rj=(Ku-λdjMu)Φdj

(10)

2.2 目标函数

基于残余力向量的基本概念，定义损伤识别的目标函数如下[14]：

{α}=(α1,α2,…,αm)T，αi∈[0,1]

maxF(α1,…,αm)=

(11)

式中αi为单元的折损因子，p为参与计算的模态数,c0=1012,c1取为1。

2.3 算法实现

1)初始化参数，设某一种群蜜蜂总量N，其中引领蜂和跟随蜂数量各占一半，引领蜂随机选择一个食物源，并且计算当前收益率。

2)进入引领蜂阶段，引领蜂在当前食物源的领域进行搜索，计算新食物源的收益率，按照模拟退火机制选择是否接受新食物源。

3)进入跟随蜂阶段，跟随蜂通过“摇摆舞”方式从引领蜂处获得信息，然后在选择最优的信息，并在最优的信息源的领域附近进行再次探索，继续按照模拟退火机制选择是否接受新食物源。

4)如果引领蜂的食物源信息在最大次迭代中均为发生变化，则认为达到了局部最优，则引领蜂变为侦查蜂，随机在解空间中选取另一个食物源代替，进行新的搜索。

5)重复以上步骤，直到达到算法终止条件。

3 数值模拟

本文采用一桁架结构模型进行数值模拟(图1)，该结构共有11个节点，26个单元，每个单元的弹性模量E=2.1×1011N/m2，密度ρ=7 800 kg/m3，横截面面积A=6.45×104m2，每跨的长度l=0.5 m。

工况1：11号单元发生30%的折损；

工况2：5号单元和21号分别发生40%的折损和35%的折损；

工况3：6号单元发生25%的折损,11号单元发生20%的折损，16号单元发生 30%的折损， 21号单元发生30%的折损，频率添加1%以及振型添加10%的高斯白噪声[15]。

对于工况1和2，目标函数采用前6阶频率和模态,进行损伤识别，初始种群,N=50，初始温度T0=500，退火系数σ=0.95，引领蜂的食物源在650次内没有得到更新，它便成为侦查蜂，算法迭代500次结束。图2为工况1中折损因子的进化迭代曲线，从图中可以看出改进的算法收敛速度更快，这充分说明改进后的算法跳出局部最优的能力得到了加强，进而能够更快地收敛到预设值0.3。两种工况的最终结果如图3和图4所示。

对于工况3，采用前9阶频率和模态进行目标函数的计算，得到相应结果如下图5所示。

图1 桁架结构Fig.1 A truss structure

图2 工况1中损伤因子的迭代曲线Fig.2 Iteration process of damage parameter in case 1

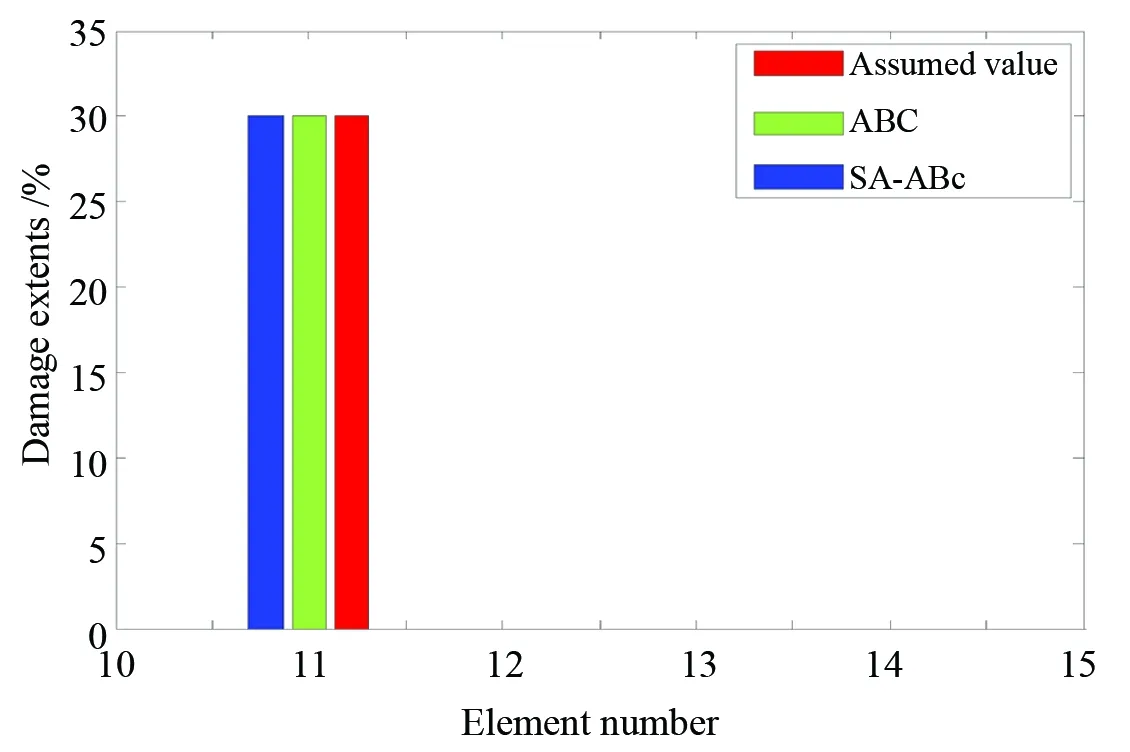
图3 工况1的识别结果(未标出的单元意味着无损)Fig.3 Identified result of case 1 (The disappeared element is intact)

图4 工况2的识别结果Fig.4 Identified result of case 2

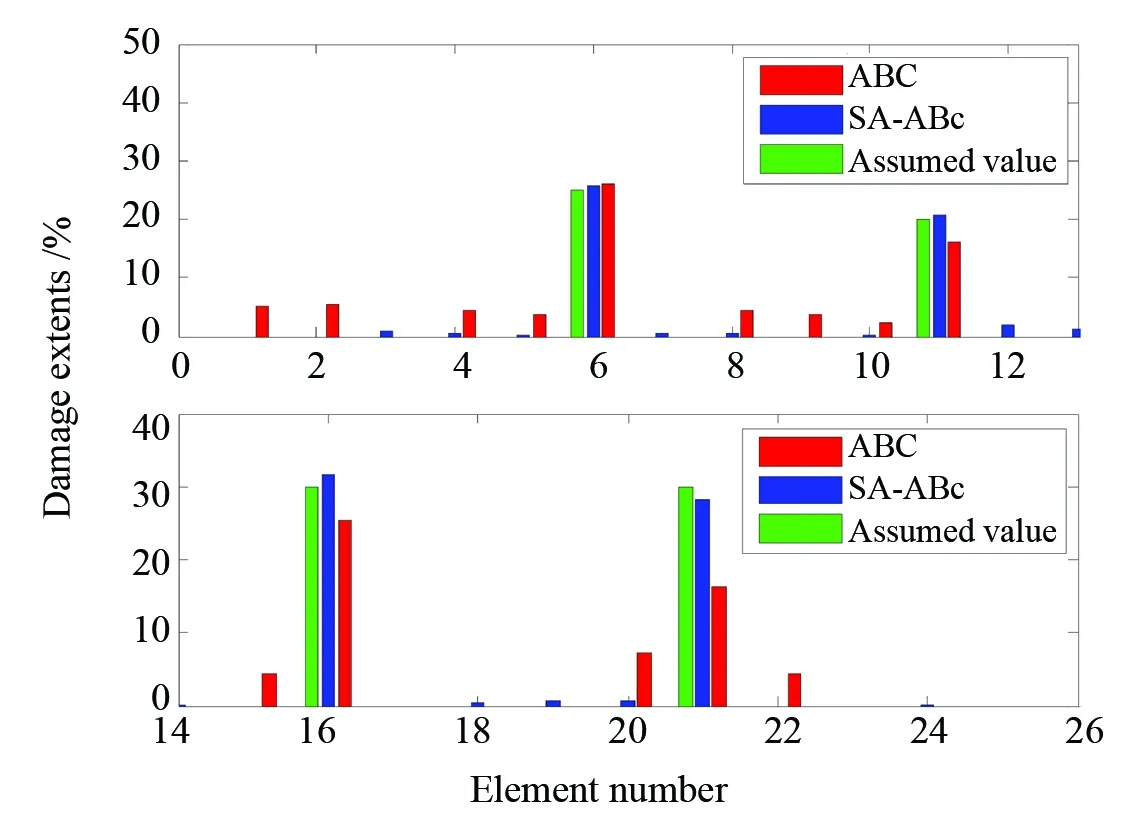
图5 工况3的识别结果Fig.5 Identified result of case 3

4 结 论

本文提出了基于模拟退火法和人工蜂群算法的损伤识别方法，即采用模拟退火机制来有效的规避“早熟”这一缺陷。接着通过构造残余力向量为目标函数，能够较准确、有效地识别桁架结构的局部损伤。在无噪声情形下，改进的算法和原始算法均能得到很好的识别结果，但改进的算法跳出局部最优的能力更强，收敛速度更快。在有噪声的情况下，改进算法得到的结果比原算法得到的更精准，说明改进后的算法抗噪能力更强,更加有利于解决实际工程问题。

[1] 刘济科，汤凯. 基于振动特性的损伤识别的方法的研究进展[J]. 中山大学学报(自然科学版)，2004, 43(6): 57-61.LIUJK，TANGK.Areviewofdamagedetectionmethodbasedonvibrationdata[J].ActaScientiarumNaturaliumUniversitiesSunYatseni, 2004, 43(6): 57-61.

[2] 杨秋伟，刘济科. 结构损伤识别的柔度灵敏度方法[J]. 中山大学学报(自然科学版)，2010, 49(1): 16-19.YANGQW，LIUJK.Structuraldamageidentificationbasedonflexibilitysensitivity[J].ActaScientiarumNaturaliumUniversitiesSunYatseni, 2010, 49(1): 16-19.

[3]LUZR,LAWSS.Featuresofdynamicresponsesensitivityanditsapplicationindamagedetection[J].JournalofSoundandVibration, 2007, 303: 305-329.

[4]LUXB,LIUJK,LUZR.Atwo-stepapproachforcrackidentificationinbeam[J].JournalofSoundandVibration, 2013, 332: 282-293.

[5]LUZR,LIUJK.Identificationofbothstructuraldamagesinbridgedeckandvehicularparametersusingmeasureddynamicresponses[J].Computers&Structures, 2011, 89: 1397-1405.

[6]MARESC,SURACEC.Anapplicationofgeneticalgorithmstoidentifydamageinelasticstructures[J].JournalofSoundandVibration, 1996, 195: 195-215.

[7]KARABOGAD,BASTURKB.ApowerfulandefficientalgorithmfornumericalfunctionoptimizationArtificialBeeColonyalgorithm[J].JournalofGlobalOptimization,2007, 39(3):459-471.

[8]KARABOGAD,BASTURKB.OntheperformanceofArtificialBeeColony(ABC)algorithm[J].AppliedSoftComputing, 2008, 8(1):687-697.

[9]SUNH,LUSH,BETTIR.IdentificationofstructuralmodelsusingamodifiedArtificialBeeColonyalgorithm[J].ComputersandStructures, 2013, 116: 59-74.

[10]DINGZH,LUZR,HUANGM.StructuraldamagedetectionusingArtificialBeeColonyalgorithmwithhybridsearchstrategy[J].SwarmandEvolutionaryComputation, 2016, 28: 1-13.

[11]XUHJ,DINGZH,LUZR,etal.StructuraldamagedetectionbasedonChaoticArtificialBeeColonyalgorithm[J].StructuralEngineeringandMechanics, 2015, 55(6): 1223-1239.

[12]ZIMMERMANDC,KAOUKM.Structuraldamagedetectioninbeamstructuresusingasubspacerotationalgorithm[J].AIAAJournal, 1992, 34(12):2341-2350.

[13]YANAJ,SHAOHS,GUOZ.Weightoptimizationforcase-basedreasoningusingmembranecomputing[J].InformationScience,2014, 287:109-120.

[14] 袁颖，林皋，闫东明，等. 基于残余力向量法和改进遗传算法的结构损伤识别研究[J]. 计算力学学报, 2007, 24(2):224-230.YUANY,LING,YANDM,etal.Damageidentificationbasedonresidualforcevectorsandimprovedgeneticalgorithm[J].ChineseJournalofComputationalMechanics,2007, 24(2):224-230.

[15]KANGF,LIJJ,XUQ,Damagedetectionbasedonimprovedparticleswarmoptimizationusingvibrationdata[J].AppliedSoftComputing, 2012, 12: 2329-2335.

Damage identification using the simulated annealing and ABC algorithm

ZHOUZitan,LIUJike,LÜZhongrong,DINGZhenghao

(School of Engineering, Sun Yat-sen University, Guangzhou 510275, China)

Artificial Bee Colony Algorithm is an optimization method based on simulating the bee’s behavior. It is a kind of swarm intelligence and used widely for engineering problem. Its main character is just to make the comparison between the solutions, at last acquiring the global optimal solution. Its convergence speed is fast but it is easy to trap into the local optimum. Simulated Annealing process is introduced in the algorithm to overcome the shortage. In the damage identification, an objective function is defined based on the residual force vector, and then the proposed method is used to identify the structural damage. A planar truss is studied as an example to illustrate the correctness and efficiency of the present method. Study shows excellent identified results can be obtained even with noisy measurements. Compared with original algorithm, the modified one has a quicker convergence rate and gets a better result, and it is not sensitive to artificial measurement noise.

ABC algorithm; simulated annealing; residual force vector; damage identification

10.13471/j.cnki.acta.snus.2017.02.015

2016-08-19 基金项目：国家自然科学基金(11172333, 11272361)；广东省自然科学基金(2015A030313126)；广东省科技计划项目(2014A020218004, 2016A020223006)

周梓檀(1992年生)，男；研究方向：结构损伤识别；E-mail:334988565@qq.con

丁政豪(1991年生) ，男；研究方向：结构健康监测；E-mail:1335969758@qq.com吕中荣(1975年生) ，男；研究方向：结构损伤识别；E-mail:lvzhr@mail.sysu.edu.cn

TB

A

0529-6579(2017)02-0088-05