基于迎风差分格式的TVD聚合物驱数学模拟

贾英，汤昌福，黄磊

（1.中国石化石油勘探开发研究院，北京 100083；2.安徽省煤田地质局勘查研究院，安徽 合肥 230088；3.中国石油勘探开发研究院，北京 100083）

基于迎风差分格式的TVD聚合物驱数学模拟

贾英1，汤昌福2，黄磊3

（1.中国石化石油勘探开发研究院，北京 100083；2.安徽省煤田地质局勘查研究院，安徽 合肥 230088；3.中国石油勘探开发研究院，北京 100083）

聚合物驱替过程中存在饱和度和聚合物质量浓度2个间断，在2个间断之间有“油墙”形成。文中分别运用特征线法（MOC）、一阶迎风差分（SPU）方法和显式全变差递减差分（TVD）方法对聚合物驱替过程进行求解，通过与特征线解进行对比，考察了SPU方法和TVD方法的数值模拟效果。研究表明：SPU方法的精度低，数值耗散严重，对2个间断特别是聚合物质量浓度间断的捕捉能力较差；高阶精度TVD方法分辨力高，但在“油墙”处会产生非物理“振荡”。利用迎风的思想，对传统TVD方法进行了改进。数值实验表明，改进的TVD方法在保持高精确度的同时，还能有效地防止非物理“振荡”的产生，具有较好的稳定性。

聚合物驱；特征线法；一阶迎风格式；TVD；非物理“振荡”

0 引言

聚合物驱能够有效改变驱替流度比，扩大扫油面积，提高波及系数和采出程度。近年来，聚合物驱提高采收率技术得到了大力推广和应用［1-9］。

聚合物驱是一个复杂的物理过程，在特定的情形下，可以运用特征线法MOC（Method of Characteristics）进行解析求解［2-3］，然而，在大部分情况下，聚合物驱都需要借助于数值方法进行研究［3，7］。在油藏数值模拟中，对流占优渗流方程主要采用单点上游迎风 SPU（Single Point Upstream）方法求解［10］。然而，SPU方法只是一阶精度，具有较强数值耗散作用，驱替过程出现的激波（间断）可能会被抹平［11-16］。高阶精度差分方法虽可提高数值模拟的精度，但直接使用容易在间断附近产生非物理“振荡”［14］。总变差递减（TVD）方法通过通量限制因子控制模拟过程中总变差的变化，在获取高阶精度的同时，还能有效防止非物理“振荡”的出现［13-14］；因而，TVD方法在油藏数值模拟中已得到推广和应用［11-15］。

本文首先运用MOC方法求解一维聚合物驱过程，通过与MOC解进行对比，进一步分析了聚合物驱SPU和TVD数值解的效果，提出了改进的TVD数值通量的重构方法，在保证了传统TVD方法的高阶精度的同时，还防止了非物理“振荡”的出现。

1 基本数学模型

聚合物驱主要通过增加水相黏度减小驱替流度比来提高采收率。在聚合物驱替过程中，还伴有吸附、水相渗透率下降等现象［1-3］。本文主要考虑了水相黏度的变化及岩石吸附对聚合物驱替的影响。并且假设：均质不可压等温流动；油水两相流动，聚合物溶于水中；驱替过程对流占优，不考虑扩散作用，且忽略重力和毛细管力对驱替过程的影响。聚合物溶液的黏度是聚合物质量浓度的函数，可用修正的水相黏度方程表示：

聚合物驱的吸附为等温吸附过程，可以用线性吸附或Langmuir吸附表示。为研究方便，假设线性吸附过程，即聚合物吸附是聚合物质量浓度的线性函数：

一维聚合物驱数学模型的水相连续方程和聚合物质量浓度方程分别为

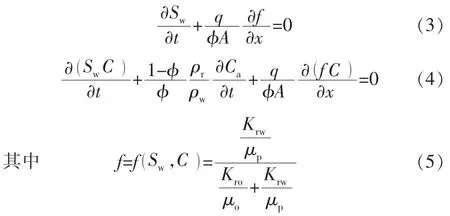
将式（3）、式（4）无量纲化，得：

将式（6）、式（7）二元双曲型方程组写成矩阵形式：

式（8）的边界条件和初始条件分别为

聚合物溶液的黏度随聚合物质量浓度呈线性变化。关于聚合物质量浓度的多项式H（C）为

研究中，取a1=1 cm3/mg，a2=9 cm3/mg，μw=1 mPa·s，μo=10 mPa·s。

采用Corey型相渗曲线，即：

取Swi=0.2，Sor=0.3，Kw=0.6，Ko=1.0，no=2，nw=2。

设注入聚合物溶液质量浓度Cin=1 mg/cm3，吸附相关常数D=0.1。油、水相对渗透率曲线及水相分流量曲线见图1。

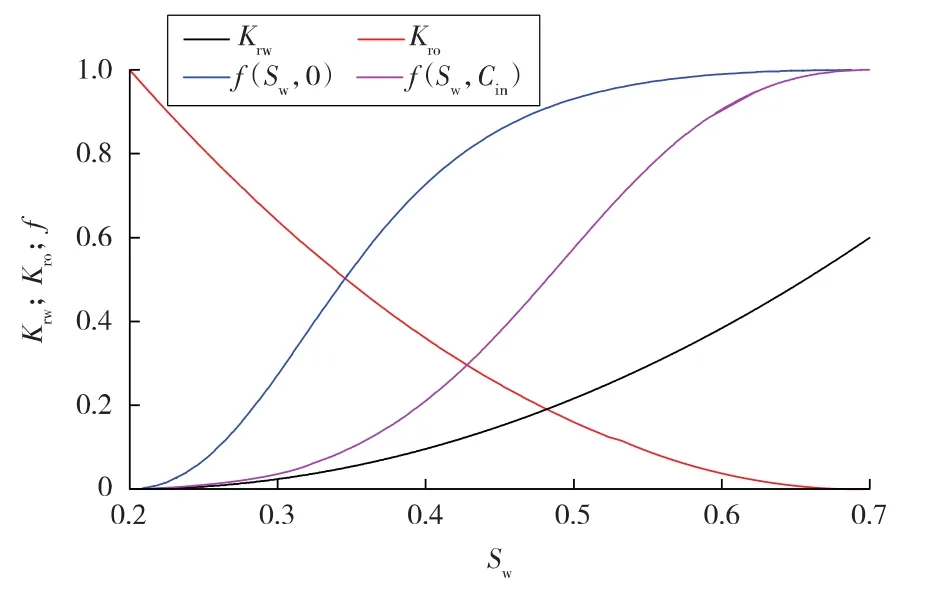
图1 油、水相对渗透率及水相分流量曲线

式（8）和式（9）组成了一维聚合物驱的Riemann问题，可以采用MOC求解。

2 一维聚合物驱特征线法

Riemann问题的解可以由简单波描述，简单波由稀疏波和激波（或接触间断）组成。式（8）存在2个特征值，分别为

图2（τ=0.1）为一维聚合物驱Riemann问题MOC模拟结果。可以看出，聚合物驱过程中存在两族波，分别为S族和C族。其中：S族波为饱和度间断，聚合物质量浓度C为常数；C族波由接触间断和稀疏波组成，在接触间断处，聚合物质量浓度C和饱和度Sw都是间断的，但其特征速度λc为常数。饱和度间断和聚合物质量浓度间断分别决定了聚合物驱见水和见聚的时间。在两族波之间存在“油墙”，饱和度保持为常数。

图2 MOC模拟饱和度和质量浓度空间分布情况

一维聚合物驱Riemann问题的MOC解具体可参考文献［2-3］。该计算结果与岩心实验CT扫描结果相一致（见图3）。

图3 水饱和度曲线及CT分析数据［16］

3 一维聚合物驱有限差分法

当初始条件和注入条件保持稳定时，一维聚合物驱可以运用特征线法（MOC）快速准确地求解。然而，实际应用过程中，饱和度和聚合物质量浓度的初始分布一般都不均匀，且注入条件也经常发生变化，此时常需要采用数值方法求解，所采用的数值方法应能够准确地捕捉聚合物驱中出现的物理现象。

式（8）的显式差分方法守恒差分格式可以表示为

不同的通量限制因子（Φ（r））构成不同的差分方法。

3.1 一阶迎风（SPU）差分方法

在油藏数值模拟中，由于具有明确的物理特点，经常采用单点上游加权迎风格式SPU［10］求解，即数值流通量采用其上游的网格值计算：

图4（τ=0.1）为不同网格数时SPU解与MOC解析解之间的对比。可以看出：网格数较少时，聚合物驱过程中的2个间断——特别是质量浓度间断——都被不同程度抹平了，SPU的数值模拟结果严重偏离精确解；随着网格数的增加，SPU数值解趋于MOC解，此时为获得一个较为精确的差分解，需要更多网格。

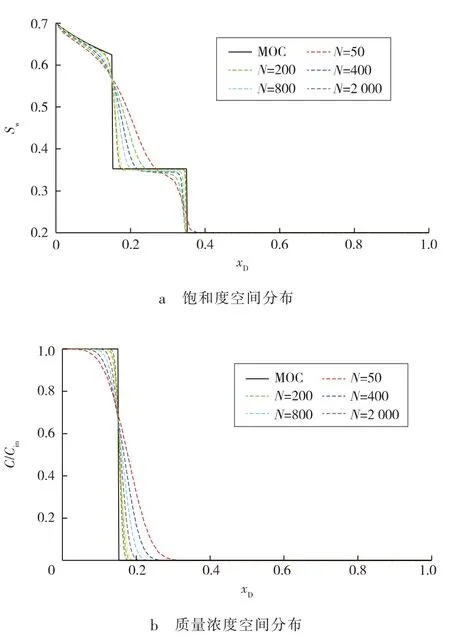
图4 一维聚合物驱不同网格数SPU差分模拟结果

上述结果表明，SPU方法对聚合物驱过程中的2个间断特别是质量浓度间断的捕捉能力较弱。这是因为：接触间断与激波不同，它不具有“自锐利”（Selfsharpening）行为，精确解的一些特征被差分方法具有的数值耗散掩盖，需要采用其他方法（例如粒子追踪方法、高阶精度差分方法等［11，17］）才能改进模拟的结果。

3.2 高分辨率显式全变差递减（TVD）差分方法

TVD差分方法能提高数值模拟的的精度，然而直接采用该方法容易在间断附近产生非物理“振荡”。为了定量研究“振荡”情形，定义时间步n的总变差［11］为

TVD差分方法通过限制总变差的增加，防止非物理“振荡”的产生，即：

此时式（14）中的通量限制因子Φ为梯度r的函数，使得在模拟区域的不同部分需采用不同的差分格式。目前，学者们提出了各种限制因子，如Min mod限制因子、Fromm限制因子、Van Leer限制因子以及Leonard限制因子等［8］。本文采用Van Leer限制因子的TVD差分方法研究一维聚合物驱过程：

图5（τ=0.1）为一维聚合物驱TVD差分方法模拟结果。通过与SPU解以及MOC解进行对比可以发现，聚合物驱数值模拟的效果得到显著改善，在较少的网格数时就能获得较为精确的数值解 （N=400）。因此，TVD差分方法捕捉间断的能力要强于SPU方法，聚合物驱差分方法应优先选择TVD差分方法，保证在较少的网格时得到更加精确的数值解。

图5 一维聚合物驱TVD差分模拟结果

然而，从图5还可以发现，TVD差分方法在提高精度的同时，却在 “油墙”处产生了非物理 “振荡”。Thiele等研究发现，增加时间差分精度、控制CFL的大小或者采用耗散性较强的限制因子（如Min mod）可以减缓“振荡”，但并不能达到消除“振荡”的目的。

3.3 迎风TVD差分方法

传统TVD差分方法在“油墙”处会出现非物理“振荡”。基于油藏数值模拟中常用的迎风思想，本文提出了新的数值流通量的计算方法，以抑制“振荡”的发生。在新的TVD差分方法中，饱和度方程中的数值流通量采用迎风格式，而质量浓度方程中的总变差通过质量浓度的TVD来限制，即：

聚合物质量浓度方程中数值通量依式（21）计算：

图6（τ=0.1）给出了改进的TVD解（U-TVD）与MOC解及传统TVD解的对比。可以发现，迎风TVD差分方法在保持TVD差分方法高阶精度的同时，还有效地抑制了“油墙”处非物理“振荡”的出现。

4 结论

1）一阶迎风（SPU）方法模拟聚合物驱能力较弱。网格数较少时，数值解严重偏离精确解；虽然可通过增加网格数改善数值模拟结果，但增加的计算代价巨大。

2）TVD差分方法能以较少网格获得较精确的数值解，聚合物驱数值模拟应尽量采用高分辨率差分方法。

3）传统TVD差分方法会在饱和度和质量浓度间断之间存在的“油墙”处产生不合理的非物理“振荡”。基于迎风思想，改进了TVD数值通量计算方法，在保证TVD方法的高精度同时，还能防止“振荡”产生，使得TVD方法更为稳定。该方法为下一步开展三维聚合物驱数值模拟奠定了基础。

图6 一维聚合物驱迎风TVD差分模拟结果

5 符号注释

μp，μw，μo分别为聚合物溶液、水相和油相黏度，mPa·s；C为聚合物在水相中的质量浓度，mg/cm3；Ca为聚合物吸附质量浓度，mg/cm3；Cin为聚合物溶液质量浓度，mg/cm3；a为吸附常数；x为空间坐标，m；t为时间坐标，s；ρr，ρw分别为岩石和水相密度，kg/m3；q为注入流量，m3/s；Sw为水饱和度；Swi，Soi分别为束缚水饱和度和残余油饱和度；φ为孔隙度；A为截面积，m2；f为水相分流量函数 （即水饱和度和聚合物质量浓度的函数）；Krw，Kro分别为水相和油相的相对渗透率；Kw，Ko分别为残余油饱和度端点水相渗透率和束缚水饱和度端点油相渗透率；τ为注入孔隙体积倍数；Vp为孔隙体积，m3；L为模型长度，m；xD为无量纲长度；D是吸附相关常数；a1，a2为常数 （通过实验取值）；nw，no分别为水相、油相相对渗透率曲线Coery系数；n和i分别表示时间和空间节点（或网格位置）；N为空间网格数；和分别为网格i的左、右数值流通量；Φ（）r为通量限制因子；r为梯度；下标分别表示上一网格和下一网格；表示在网格位置的质量浓度差比值。

［1］NEEDHAM R B，DOE P H.Polymer flooding review［J］.Journal of Petroleum Technology，1987，39（12）：1503-1507.

［2］POPE GARY A.The application of fractional flow theory to enhanced oil recovery［J］.SPE Journal 1980，20（20）：191-205.

［3］PATTON J T，COATS K H，COLEGROVE G T.Prediction of polymer flood performance［R］.SPE 2546，1971.

［4］蒋明.齐40块稠油油藏聚合物驱可行性室内实验研究［J］.断块油气田，1998，5（1）：45-49.

［5］宋考平，杨二龙，王锦梅，等.聚合物驱提高驱油效率机理及驱油效果分析［J］.石油学报，2004，25（3）：71-74.

［6］方文超.陆上稠油油田多轮次聚合物驱提高采收率方法［J］.断块油气田，2015，22（5）：619-622.

［7］芦文生.绥中36-1油田聚合物驱数值模拟研究［J］.中国海上油气，2002，16（5）：333-340.

［8］周丛丛.大庆油田一、二类油层聚合物驱注采指标变化规律［J］.断块油气田，2015，22（5）：610-613.

［9］侯健，李振泉，王玉斗，等.考虑扩散和吸附作用的聚合物驱替过程渗流数值模拟［J］.计算物理，2003，20（3）：239-244.

［10］MALLISON B T，GERRITSEN M G，JESSEN K，et al.Higher-order upwind schemes for two-phase，multi-component Flow［R］.SPE 79691，2005.

［11］THIELE M R，EDWARDS M.Physically based higher order godunov schemes for compositional simulation［R］.SPE 66403，2001.

［12］LEER V B.Towards the Ultimate conservative difference Scheme，V-A second-order sequel to Godunov′s method［J］.Journal of Computational Physics，1979，32（1）：101-136.

［13］HARTEN A.High resolution schemes for hyperbolic conservation laws［J］.Journal of Computational Physics，1983，49（3）：357-393.

［14］RUBIN B，EDWARDS M G.Extension of the TVD mid-point scheme to higher order accuracy in time［R］.SPE 25265，1993.

［15］BRENIER Y，JAFFRÉ J.Upstream differencing for multiphase flow in reservoir simulation［J］.Siam Journal on Numerical Analysis，1991，28（3）：685-696.

［16］SU S.Laboratory investigation of polymer-flooding，ASP-flooding，and foam-flooding in heavy oil system［D］.Calgary：University of Calgary，2012.

［17］JUANES R，LIE K A.Numerical modeling of multiphase first-contact miscible flows.Ⅱ.Front-tracking/streamline simulation［J］.Transport Porous Media，2008，72（1）：97-120.

（编辑 李宗华）

Mathematical simulation of polymer flooding with upstream-TVD solution

JIA Ying1,TANG Changfu2,HUANG Lei3
(1.Petroleum Exploration and Production Research Institute,SINOPEC,Beijing 100083,China;2.Exploration Research Institute, Anhui Provincial Bureau of Coal Geology,Anhui 230088,China;3.Research Institute of Petroleum Exploration&Development, PetroChina,Beijing 100083,China)

For polymer flooding,there are two discontinuities of saturation and concentration,between which"oil bank"exists.The polymer flooding was investigated with method of characteristics(MOC),single point upstream(SPU)finite difference method and explicit total variation diminishing(TVD)finite difference method respectively.Based on the solution of MOC,performance of simulation results of both SPU and TVD were evaluated.It is suggested TVD exhibits a better numerical performance while the SPU scheme suffers numerical diffusion badly.The conventional TVD method is modified on the calculation of numerical flux,so that non-physical oscillation can be prevented on the"oil bank"between the two discontinuities.Numerical tests demonstrate that the upstream-TVD can achieve better stability than the conventional TVD method.

polymer flooding;MOC;SPU;TVD;non-physical oscillation

TE357.46+1

A

10.6056/dkyqt201703017

2016-12-12；改回日期：2017-03-09。

贾英，女，1980年生，高级工程师，博士，油气田开发工程专业。E-mail：jiaying.syky@sinopec.com。

贾英，汤昌福，黄磊.基于迎风差分格式的TVD聚合物驱数学模拟［J］.断块油气田，2017，24（3）：373-377.

JIA Ying，TANG Changfu，HUANG Lei.Mathematical simulation of polymer flooding with upstream-TVD solution［J］.Fault-Block Oil&Gas Field，2017，24（3）：373-377.