金钱弄水库劈裂灌浆裂隙倾角与扩散半径分析

2017-06-06赖昌亮

黑龙江水利科技 2017年3期

关键词：牛顿流体库容倾角

赖昌亮

(桂林利源水电建设有限责任公司，广西桂林 541000)

金钱弄水库劈裂灌浆裂隙倾角与扩散半径分析

赖昌亮

(桂林利源水电建设有限责任公司，广西桂林 541000)

根据多年工作实践经验与总结，文章推导出水库岩体裂隙倾角对灌浆扩散半径的影响，并推导出牛顿流体和宾汉流体扩散半径的计算公式，运用所推导的公式分析了金钱弄水库劈裂灌浆过程中倾角对灌浆效果的影响，并提出调整灌浆参数，提高灌浆效果的相关建议，以期对类似工程提供指导借鉴。

劈裂灌浆；裂隙倾角；扩散半径；牛顿流体；宾汉流体

1 工程实例

金钱弄水库于1958年9月开工，该工程的设计工作由原地区勘测设计队承担，最初设计库容仅28万m3，1962年计划增开两条引洪渠，库容增至74.5万m3(有效库容)，到1965年扩大设计时，决定加高主副坝、增开引洪沟两条，引洪面积15.35km2，连同原库区面积2.2km2，水库总面积为17.55km2，库容扩大到460万m3，有效库容为359万m3。金钱弄水库是以灌溉为主，兼顾防洪、水产养殖等功能的小(Ⅰ)型水库。水库总库容403.2万m3，调洪库容35.4万m3，调节库容323.7万m3。工程设计灌溉面积1.23万亩，有效灌溉面积427hm2，保护下有人口1.23万人、耕地1533.3hm2。

在对金钱弄水库基础灌浆效果进行声波检测过程中，对检测结果进行比较分析发现，在距离不超过1m的两个相邻检查孔内，所检测到的声波波速差异很大，声波波速的大小间接反映了岩体质量，而通过灌浆后岩体声波波速的变换也可以反映灌浆效果的好坏，灌浆扩散范围是否均匀可以直接通过分析同一岩体灌浆后声波波速是否存在差异而进行判断，在实际水库工程劈裂灌浆过程中，可以通过适当调整孔距、排距及其他灌浆参数，并不断进行灌浆后声波波速差异的比对与分析，以达到最优的灌浆效果。

2 裂隙倾角与灌浆扩散半径分析

由于存在裂缝倾角，在浆液自身重力的作用下，浆液并非按照规则的圆周进行扩散，而是按照一个光滑连接两段长短轴而形成的椭圆弧封闭曲线进行扩散，如图1所示，大椭圆区域内裂隙倾向与浆液扩散方向构成锐角，所以当扩散方向和裂隙倾向同向时，扩散半径最大；小椭圆区域裂隙倾向与浆液扩散方向构成钝角，而当扩散方向与离析倾向正好相反是，扩散半径最小，浆液扩散的最大半径和最小半径是实际工程中最为关心的两个量。

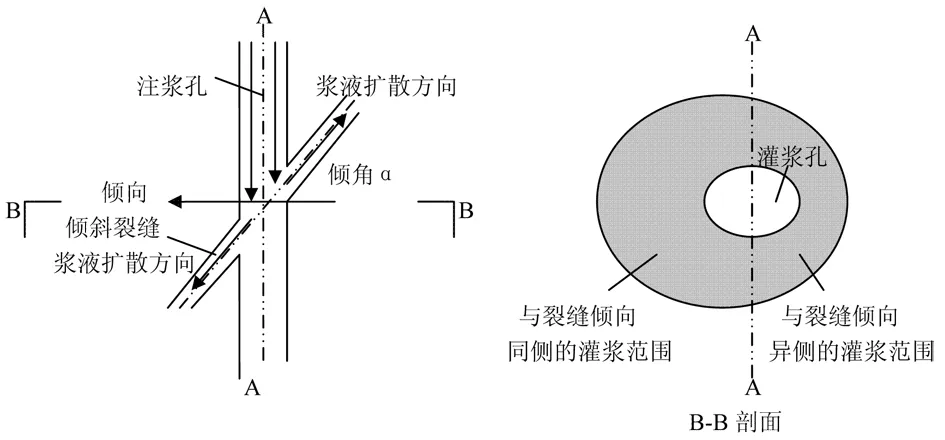
图1 倾斜裂隙灌浆孔及扩散范围示意图

2.1 按牛顿流体考虑

借鉴牛顿流体在水库裂缝流动的特性，可以概括出灌浆平板裂隙模型，模型中裂隙的流体单元符合：

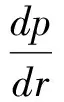
(1)

式中：dr为浆液扩散方向；dz为垂直浆液扩散平面方向；p为浆液压力；τ为浆液的剪切力。对于式(1)中的牛顿流体，必须满足牛顿摩阻力定律，即：

(2)

将裂隙倾角α考虑进来，结合式(1)牛顿流体的流动特性及扩散半径的推导过程，经过变换，可以求得扩散半径r处的压力：

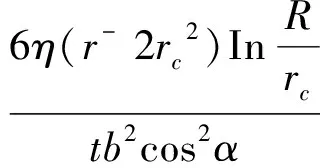
(3)

式中：p与pc分别为扩散半径r处和灌浆孔内的浆液压力；η为浆液黏度，kPa·s；R为扩散半径最大值；rc为钻孔半径，cm；b为裂隙宽度，cm；t为灌浆持续时间。

结合图1中对倾斜裂隙灌浆孔及扩散范围的描述，并考虑对灌浆模型进行改进后，可以将裂缝内浆液压力等分为两部分，一部分为p1(即灌浆孔内浆液压力pc流动损失后的压力)，另一部分为p2(即浆液在倾斜裂缝内由于自重而产生的压力)，则距离灌浆孔中心轴r的浆液压力为：

p=p1+p2

(4)

式中：p1可通过(3)求得，p2可根据浆液重度γJ(kPa/cm)求得，公式为：

p2=±γJ(r-rc)tanα

(5)

将(3)(4)(5)式综合考虑，可得：

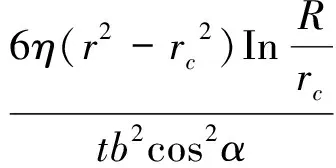
(6)

在式(5)(6)中，“+”表示裂隙内浆液扩散方向与裂隙倾向完全一致，而“-”表示两者方向相反。随着p的逐渐下降直至地下水压力p0(kPa)时，此时t=T，r=R，可以通过下式计算灌浆最大扩散半径R，cm：

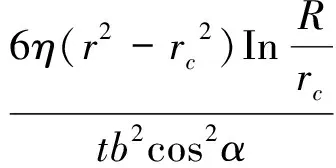
(7)

2.2 按宾汉流体考虑

牛顿流体是纯黏性流体，影响其流动的主要参数就是其黏度，与此不同的是，宾汉流体是黏塑性流体，除了黏度会影响其流动外，还有浆液的黏聚力(或抗剪断强度)，故而宾汉流体的流动规律如下：

(8)

将(8)带入式(1)并且变形可以得到：

(9)

将式(9)进行与按牛顿流体相同的推导与转换，最终便可求得宾汉流体型浆液在平滑裂隙中的扩散半径隐式计算公式，如下：

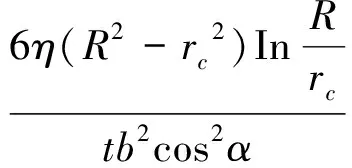
(10)

式中：c为宾汉流体型浆液的黏聚力，kPa；其他符号意义同前。

2.3 计算与分析

为了分析金钱弄水库大坝劈裂灌浆裂隙倾角对扩散半径所可能发生的影响，必须根据所推导的公式进行一系列计算。在计算时，根据工程劈裂灌浆实际中的各项灌浆参数，对于牛顿流体假设η=5.0×10-6kPa·s，γ=0.12kPa/cm，pc=5000kPa，由于不考虑地下水压力，故p0=0，rc=7.6cm，b=0.02cm，T=2400s；对于宾汉流体假设η=1.3×10-4kPa·s，γ=0.19kPa/cm，c=3.0×10-3kPa，其余参数取值同牛顿流体。将上述数值代入公式(7)和(10)，计算出不同倾角下所对应的浆液扩散半径，计算结果详见表1。

表1 浆液扩散半径R的计算结果 cm

表1的计算结果表明，牛顿流体和宾汉流体均存在随着裂隙倾角的扩大，钻孔两侧的扩散半径差值先增大后减小的现象，并且在同一倾角和劈裂灌浆条件下，牛顿流体的扩散半径差值远大于宾汉流体，进一步分析发现，当倾角在50°左右时，两侧扩散半径差值均达到最大值，此情况下灌浆扩散范围的均匀性与灌浆效果最差，故而可将此时倾角作为最不利倾角。