基于双闭环的单相电压型整流器PFC非线性控制
2017-06-05张珍珍徐利梅王玉
张珍珍,徐利梅,王玉
(西南民族大学电气信息工程学院,四川 成都 610041)
基于双闭环的单相电压型整流器PFC非线性控制
张珍珍,徐利梅,王玉
(西南民族大学电气信息工程学院,四川 成都 610041)
考虑到整流器的非线性时变特性,首先采用状态空间平均法建立了单相电压型整流器的数学模型。然后,基于李雅普诺夫稳定性理论,设计了双闭环控制系统,其中,通过电流内环控制实现整流器交流侧单位功率因数,电压外环控制率的设计解决了整流器直流侧电压稳定问题。在Matlab/Simulink平台中,搭建单相电压型整流器模型,在电网电压扰动和负载扰动2种情况下,对理论分析结果进行验证。结果表明,直流侧输出电压稳定的同时,网侧电流与电网电压同频同相,实现了两者之间的同步。
状态空间平均法;李雅普诺夫稳定性;电流内环;电压外环;功率因数校正(PFC)
单相电压型整流器由于其能量的双向流动、可以实现交流侧单位功率因数和为负载提供稳定的直流电压而备受关注。得到了广泛的应用和研究(特别在电机拖动方面)[1-3]。
电压型整流器的控制目标有2个:一是调节直流侧电压使其维持在给定值;二是调节交流侧的功率因数。目前,应用于该系统的控制方法可以归结为2大类:单环PFC控制和级联型电流模式控制(双环控制)。文献[4-5]采用无源控制实现整流器功率因数校正。基于双闭环的整流器PFC控制被提出,最常用的控制方法有PID控制[6]。
本文针对单相电压型整流器的非线性特性和混合特性,将状态空间平均法引入到建模中,并以此为基础设计了双闭环控制系统,其中,通过电流内环控制实现整流器交流侧单位功率因数,电压外环控制率的设计解决了整流器直流侧电压稳定问题。其次,根据Lyapunov稳定性定理,分析了基于双闭环的单相电压型整流器的稳定性。最后在Matlab/Simulink平台中,搭建单相电压型整流器模型,在电网电压扰动和负载扰动2种情况下,对本文所设计的控制方法进行验证。
1 单相电压型整流器动态模型
单相电压型PWM整流器原理图[7]如图1所示,由4个IGBT反并联二极管构成H桥变换器,通过控制上桥臂和下桥臂的导通、关断时间和次序来改变直流侧电压Ud。
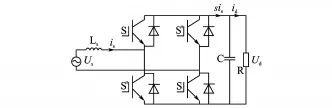
图1 单相电压型整流器电路原理图Fig.1 The schematic diagram of the single-phase voltage rectifier
图1中,Us为电源电压,is为电源电流,Ls为储能电感,C为电容,R为负载电阻,id为负载电流。
假设:1)忽略电源内阻的影响;2)H桥变换器中4个IGBT反并联二极管为理想开关,忽略其开通关断延时和功率损耗。
基于假设,利用分段线性的思想,根据基尔霍夫电压、电流定律,单相电压型PWM整流器的数学模型为
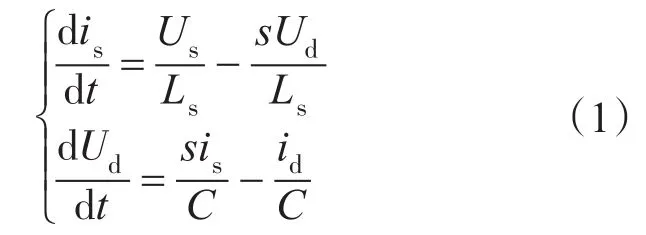
式中:s为在离散集合中取值的开关函数。
由于开关函数的不连续性,导致式(1)为1组对时间不连续的微分方程组,求解将非常困难。当开关频率很高时,状态空间平均法将是行之有效的解决办法。采用开关函数在1个开关周期内的平均值代替开关函数本身,将式(1)改写为对时间连续的平均值状态方程。

2 基于双闭环的单相电压型整流器PFC控制
如图2所示,设计的双闭环控制器,即电压外环控制和电流内环控制,实现1)输出稳定的电压,使ud跟踪udref的变化;2)单位功率因数控制,使交流侧功率因数为1。
2.1 电流内环控制器设计
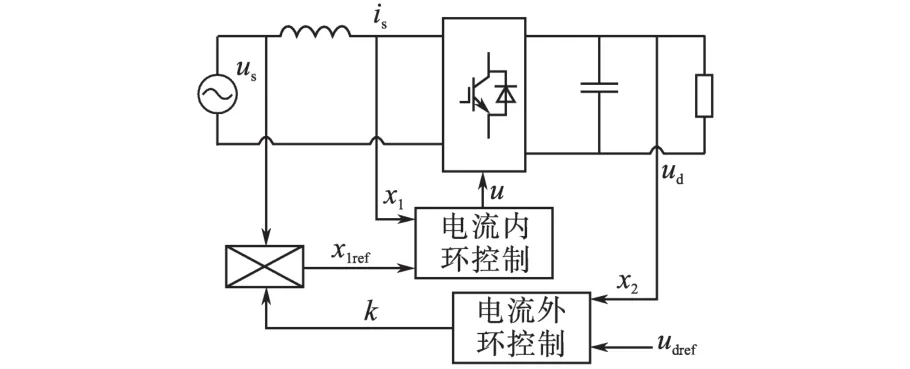
图2 基于双闭环控制的单相电压型整流器PFC控制Fig.2 PFC control of the single-phase voltage rectifier base on dual-loop
为实现控制目标2),即is必须与us同相,因此令其中是任意正的时变参数。
定义误差e1=x1-x1ref,则

取控制信号
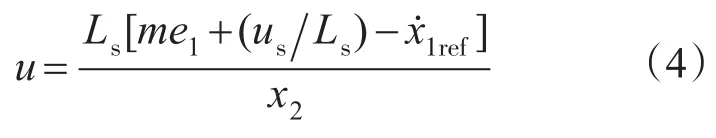
式中:m为任意正数。
2.2 电压外环控制器设计
根据控制目标1)要求,变流器输出电压ud保持在其给定值udref上,即令引入误差其中则

考虑到在忽略损耗情况下,单相电压型逆变器输入功率Pin=ux1x2与输出功率Pout=x1us是相等的,即x1us=ux1x2。由于x1=kus+e1,则,结合式(2),可得:
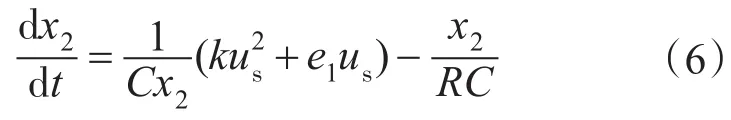
则引入式(6),式(5)改写为
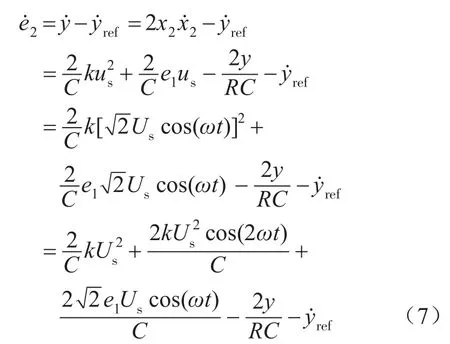
引入虚拟控制率:
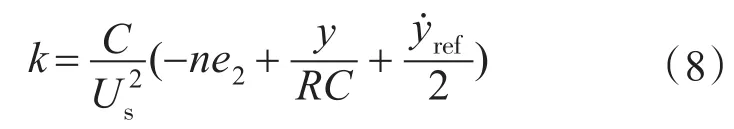
式中:n为任意正数。
考虑到如式(4)所设计的控制率u,虚拟控制率k必须一阶可导,则k需满足:
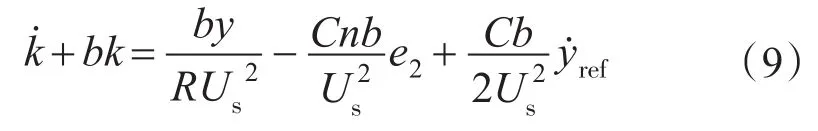
2.3 基于Lyapunov稳定性证明
定理1:单相电压型整流器在满足假设时,设计如图2所示的电流内环控制率u(由式(4)推导)和电压外环控制率k(由式(9)推导),则如下式所示的闭环系统:
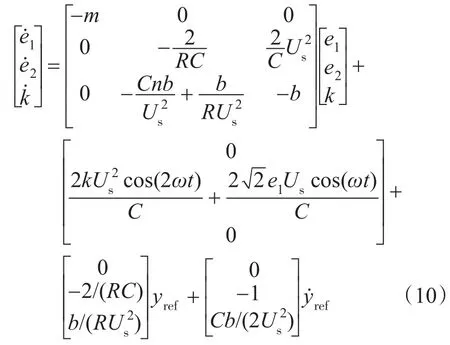
有以下性质:
1)误差e1,e2,k依赖于ε,且ε=1/ω,即

2)若yref=u2
dref是周期为Nπ/ω的周期函数,且N为正整数,则存在1个ε*>0,使得对一切ε<ε*(即ω>1/ω*),使得
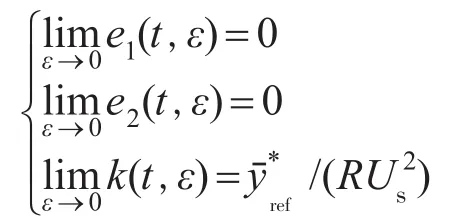
3)设计参数m,n,b,使得式(10)所示系统中的矩阵
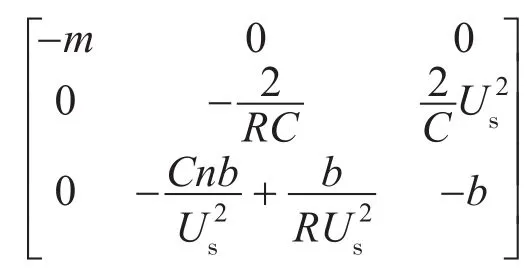
注1:由定理1可知,单相电压型整流器稳定电压输出和单位功率因数的控制目标实现依赖于ε=1/ω,当ε越小,即交流侧的角频率ω越大,则变流器输出电压ud能更好地保持在其给定值udref上,且交流侧功率为1。本文将通过仿真,验证ω=100π(即频率为50 Hz)时,基于所设计的双闭环控制器,能够实现输出电压稳定的同时,保证网侧电流与电网电压同频同相。
证明如下:
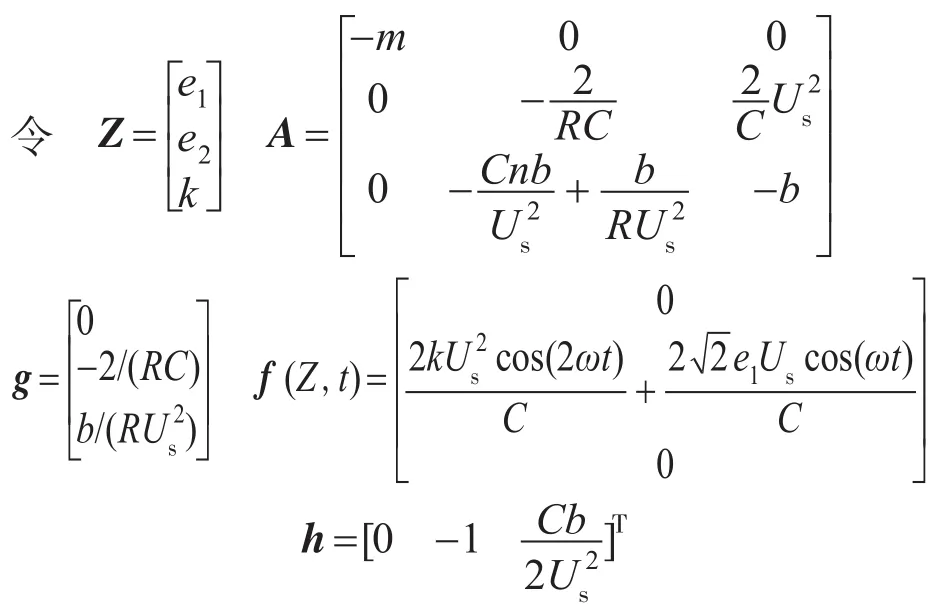
则式(10)改写为
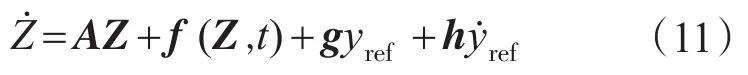
式(11)所示系统为周期时变系统,因此,本文采用平均值理论分析该系统的稳定性[8]。
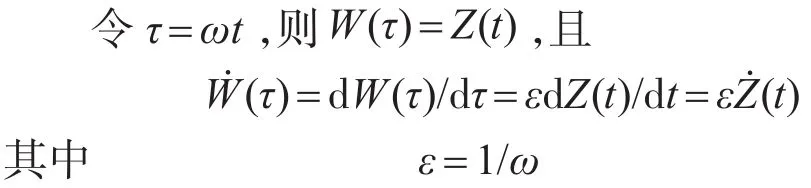
式(11)改写为
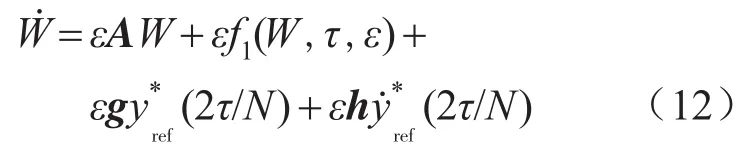
其中

根据System Averaging Theory[8],由式(12)所示系统的稳定性可以由下式所示系统得出:
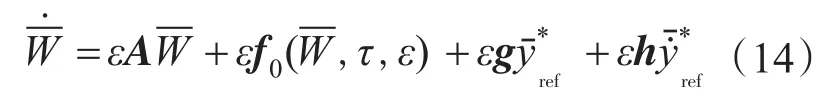
其中
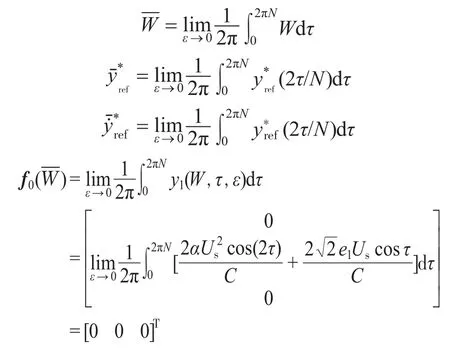
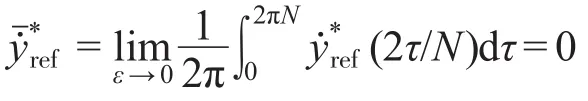
公式(14)所示的系统可简化为
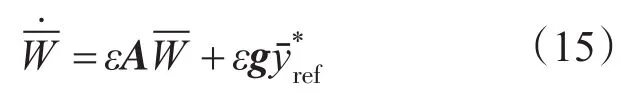
式(15)所示的系统存在唯一的平衡点W*。
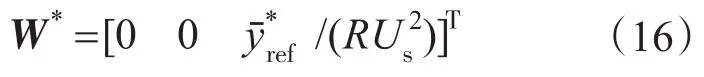
设计参数m,n,b使得矩阵A为Hurwitz,则如式(16)所示的平衡点是全局渐进稳定的[9]。
根据Theorem4.1[10],存在1个ε*>0,使得对一切ε<ε*,如式(14)所示的系统有1个周期为2π的解且

考虑到W(τ)=Z(t)且τ=ωt,则如式(10)所示系统有一个周期为2π/ω的解Z(t)=Z(t,ε),且

即
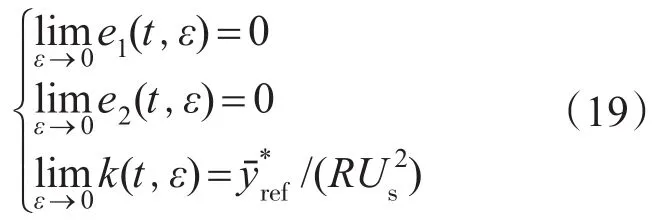
3 仿真及分析
如图3所示,本节将所设计的双闭环控制器应用于单相电压型整流器仿真模型。针对电网电压扰动和负载扰动2种状况进行了仿真验证。
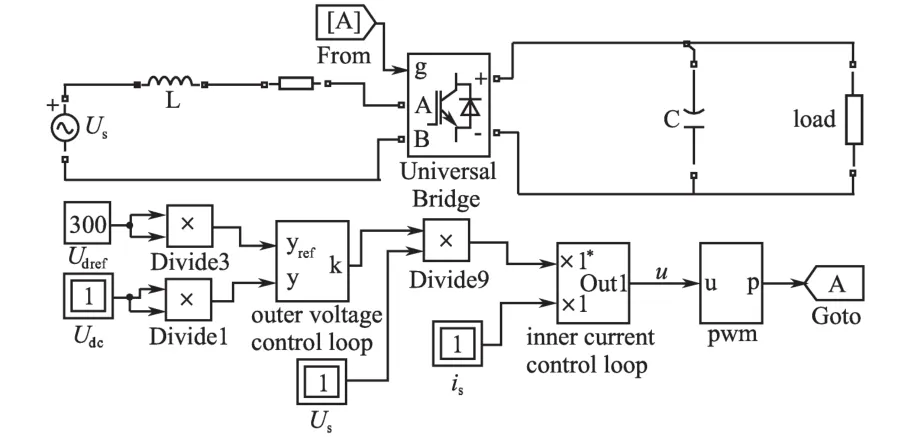
图3 基于双闭环的单相电压型整流器PFC控制仿真模型Fig.3 The simulation model of the PFC control for the single-phase voltage rectifier based on dual-loop
系统参数为:Us=220 V,Udref=300 V,Ls=2 mH,C=1 mF。系统控制参数为:m=1 500,n=20。仿真中整流器的PWM调制中,调制波的周期为0.02 s,载波的频率为15 000 Hz。
3.1 电网电压扰动情况
为了验证本文所提出的PFC控制算法在电网电压波动下的性能,本文在仿真中采用Matlab/ Simulink中的“Controlled Voltage Source”模拟t= 0.2~0.6 s时,电网电压施加了-10%扰动,而在t=0.6~1s电网电压施加了+10%扰动。如图4所示,电网电压在扰动前,即0.2 s前,电压为;在t=0.2~0.6 s时,电网电压在施加了-10%扰动,即电压为;在t=0.6~1 s时,电网电压施加了+10%扰动,即电压为342 V。

图4 电网电压波动下网侧电压电流波形Fig.4 The voltage and current of the grid side under the grid voltage disturbance
由图4可以看出网侧电流与电网电压相位一致,实现了网侧电压电流同步。为了更直观地展示,图5对图4中t=0.6~1 s时的波形进行了放大。如图5所示,在电网电压施加了+10%扰动时,网侧电压、电流波形仍然是同步的,说明本文所提出的PFC控制算法在电网电压波动下能够实现单相电压型整流器的单位功率因数控制。
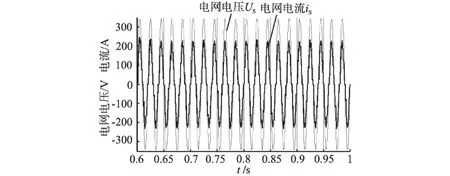
图5 电网电压波动下网侧电压电流波形局部放大图Fig.5 The partial enlarged view of the grid-side voltage and current under the grid voltage disturbance
图6是在电网电压波动下单相电压型整流器直流侧电压输出波形。直流侧电压能够稳定在其设定值Udref300 V,且响应速度快,无超调,无稳态误差。
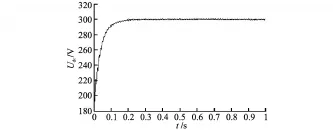
图6 电网电压波动下直流侧电压波形Fig.6 The output voltage of the DC side under the grid voltage disturbance
3.2 负载扰动情况
为了验证本文所提出的PFC控制算法在负载扰动下的性能,本文在仿真中利用”Matlab/ Simulink”中的”Breaker”模拟在t=0.3 s负载由10 Ω减少到5 Ω,而在t=0.6 s负载增加到20 Ω。
图7是负载出现扰动时单相电压型整流器直流侧电压输出波形。直流侧输出电压能够稳定在其设定值Udref300 V,波动很小,表明系统有较好的抗干扰性。
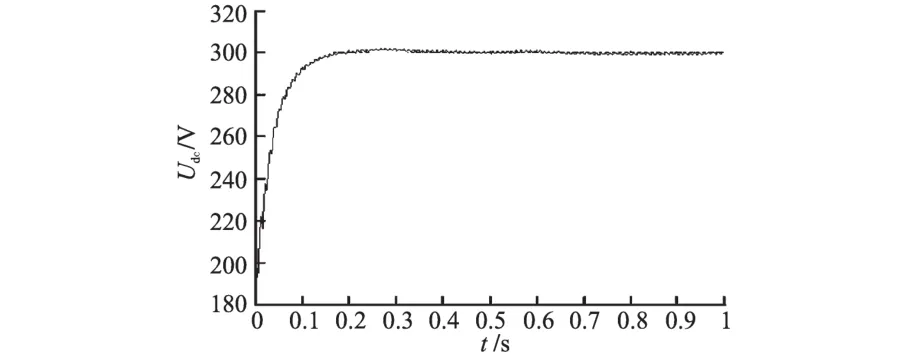
图7 负载扰动下直流侧电压波形Fig.7 The output voltage of the DC side under the load disturbance
图8是负载出现扰动时单相电压型整流器网侧电压、电流波形。图8中,无论在t=0~0.3 s负载为10 Ω时,还是在受扰动后t=0.3~0.6 s,负载为5 Ω时,网侧电压、电流波形仍然是同步的。
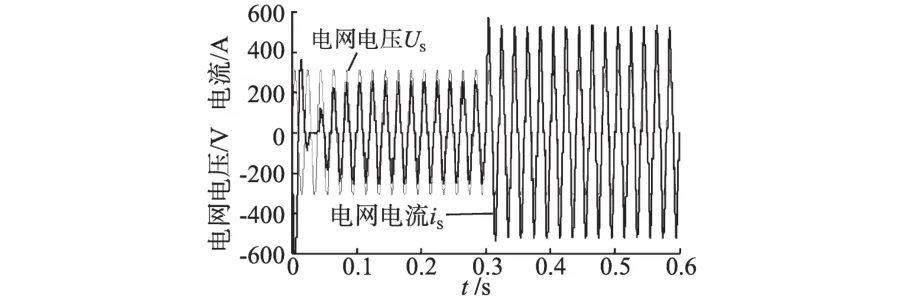
图8 负载扰动下网侧电压电流波形Fig.8 The voltage and current of the grid side under the load disturbance
4 结论
本文建立了单相电压型整流器的平均值状态数学模型,考虑到整流器的非线性时变特性,设计了双闭环控制系统。最后在Matlab/Simulink平台中,搭建单相电压型整流器模型,对本文所设计的控制方法进行验证,仿真结果表明无论在电网电压扰动下,还是在负载扰动下,本文所设计的控制器,能够实现单相电压型整流器的单位功率因数控制和输出直流电压稳定,并具有较好的动态响应和稳态特性。
[1]El Magri A,Giri F,Abouloifa A,et al.Robust Control of Synchronous Motor Through AC-DC-AC Converters[J].Control Engineering Practice,2010,18(5):540-553.
[2]刘晓艳,卢健康,马艳.整流器直接功率控制系统的优化设计[J].微特电机,2013,41(3):48-51.
[3]刘翔,曹萍,陈致远,等.直流调速系统与Matlab仿真[J].电气传动,2013,43(4):12-16.
[4]Escobar G,Chevreau D,Ortega R,et al.An Adaptive Passivity-based Controller for a Unity Power Factor Rectifier[J],IEEE Trans.Control Syst.Technol.,2001,9(4):637-644.
[5]吕学志,康忠健,梅永超.基于无源性理论的电压不平衡条件下PWM整流器非线性控制策略[J].电力系统保护与控制,2013,41(6):71-76.
[6]Ye Y,Kazerani M,Quintana V H Modeling.Control and Implementation of Three-phase PWM Converters[J].IEEE Trans.on Power Electronics,2003,3(18):857-864.
[7]李向明,刘当.单相PWM整流器的小信号模型仿真[J].仪表技术,2010(6):65-66.
[8]Khalil H.Nonlinear Systems[M].NJ,USA:PrenticeHall,2003
[9]Parks P C.A New Proof of the Routh-hurwitz Stability Criterion Using the Second Method of Lyapunov[J].Proc.Camb. Phil.Soc.Math.Phys.Sci.,1962,58(1):694-702.
[10]Zhifen Z,Tongren D,Wenzao H,et al.Qualitative Theory of Differential Equations[M].Rhode Island:American Mathematical Society,1992.
Power Factor Correction Nonlinear Control for the Single-phase Voltage Rectifier Based on Dual-loop
ZHANG Zhenzhen,XU Limei,WANG Yu
(College of Electrical and Information Engineering,Southwest University for Nationalities,Chengdu 610041,Sichuan,China)
Taking the nonlinear time-varying characteristics of the rectifier,a mathematical model of the singlephase voltage rectifier was built by using the state-space averaging method.Then,based on the Lyapunov stability theory,the dual-loop controller was designed.The unity power factor of the AC-side was fulfilled by the control of the inner-current loop,and the control law of the outer-voltage loop was designed to achieve the stable of the AC-side voltage.In the Matlab/Simulink,the simulation model of the single-phase voltage rectifier was built to verify the effectiveness of the proposed control method under the disturbance of the grid voltage or the load.The simulation results show that the DC-side voltage is stable,and the grid-side current is sinusoidal and in the same frequency and phase with the AC supply voltage.
state-space averaging method;Lyapunov stability;inner-current loop;outer-voltage loop;power factor correction(PFC)
TM34
A
10.19457/j.1001-2095.20170507
2016-05-02
修改稿日期:2016-10-20
西南民族大学中央高校基本科研业务费专项资金(2014NZYQN13);国家民委科技项目(14XNZ019);四川省教育厅2015年度科研计划(15ZB0483)
张珍珍(1985-),女,博士,讲师,Email:Zhangzhenzhen.isit@gmail.com
