变压器П形模型的教学实践

赵 霞， 罗 兰， 余渌绿， 李欣怡

(重庆大学 电气工程学院， 重庆 400044)

变压器П形模型的教学实践

赵 霞， 罗 兰， 余渌绿， 李欣怡

(重庆大学 电气工程学院， 重庆 400044)

变压器П形模型(也称为等值变压器模型)是“电力系统稳态分析”课程的一个教学难点。根据电网建模的实际需求，变压器П形模型主要有三种应用场景。现有教材大多详细讨论了变压器П形模型的推导过程以及第一种应用场景，而对另外两种场景的分析和讨论都不够充分。本文重点讨论另外两种场景下变压器П形模型的应用，详细推导了两种场景下理想变压器变比的取值。

电力系统分析；变压器П形模型；模型推导

0 引言

变压器П形模型(又称等值变压器模型)，是在变压器Γ形或T形模型基础上发展起来的一种能等值地体现变压器电压变换功能的模型[1]。等值变压器模型是建立多电压等级复杂电网等值电路的基础，在电力系统计算和分析中有着广泛的应用，一直以来都是“电力系统稳态分析”课程的一项重要教学内容。

与Γ形或T形模型类似，变压器П形模型也有“有名制”和“标幺制”之分；但比Γ形或T形模型更为复杂的是，П形模型又可以分为三种适用于不同建模需求(应用场景需求)的模型。然而，现有教材(如文献[1]、[2]等经典教材)大多只详细推导了П形模型的有名值电路(即后文的“场景一”)，对后文述及的其它两种应用场景的分析和讨论都不够充分。

学生普遍反映对模型的理解和掌握有困难，变压器П形模型因此也成为“电力系统稳态分析”课程的一个教学难点。

本文尝试弥补现有教材的不足，讨论变压器П形模型在另外两种场景中的应用，重点推导在这两种场景下理想变压器变比的取值，期望能为这一难点内容的教学实践提供一些参考。

1 变压器П形模型的基本原理

以双绕组变压器为例，当不考虑励磁支路时，任何一台实际变压器都可以等值为一台理想变压器与变压器本身阻抗的串联电路[1]。以图1所示的简单4节点电网为例，假设双绕组变压器的实际变比为k，归算到节点3侧的有名值阻抗为ZT，则可以用图2中虚框部分来等值实际的变压器。图中，Z12和Z34分别为线路1-2和3-4的实际阻抗(未经电压等级归算的原始阻抗)，忽略线路对地电容。

图1 简单电网

在图2的基础上，根据电路的端口等值条件，可以进一步建立图3所示的有名值等值电路，图中虚框内的部分即为变压器的П形模型。图3用导纳参数表示П形模型三条支路的参数，YT=1/ZT。

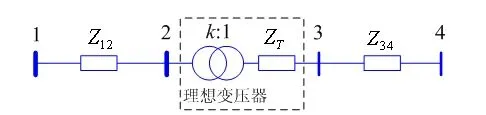
图2 含有理想变压器的等值电路

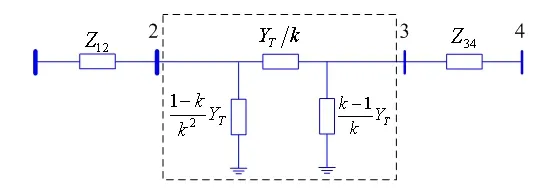
图3 变压器的П形模型

由于图3中的线路阻抗都是未经电压等级归算的线路实际阻抗，因此，当变压器变比k变化时，只需要修改变压器П形模型三条支路的参数即可。这也是变压器П形模型相对于Γ形或T形模型的一大优点。

显然，如果要考虑变压器的励磁支路或线路的对地电容支路，只需要在相应的节点接入对地支路即可(励磁支路以归算到低压侧、并接入节点3为宜)。

2 变压器П形模型的应用场景

2.1 三种应用场景

应用变压器П形模型建立电网的等值电路时，关键在于如何确定图2中理想变压器的变比以及串联阻抗的数值。

根据电网建模的实际需求，主要可以分为以下三种应用场景：

场景一：有名值，线路参数未经归算，变压器参数归算到某一侧(通常为低压侧)。

场景二：有名值，线路和变压器参数已按某个变比(例如变压器的额定变比U1N/U2N)归算到高压侧。

场景三：标幺值，线路和变压器参数已按选定的基准电压U1B、U2B和基准容量SB折算为标幺值。

可见，场景一要解决的问题就是如何应用变压器П形模型来建立电网的有名值等值电路，实际上也就是图1～图3所示的变压器П形模型的推导过程。显然，这种场景下，取变压器的实际变比作为理想变压器的变比，取变压器归算到低压侧的阻抗作为串联阻抗。

现有的教材一般给出的变压器П形模型的详细推导过程，就是详细说明了场景一中理想变压器变比以及串联阻抗如何取值，而对于另外两种应用场景的分析和讨论都不充分。本文详细说明变压器П形模型在场景二和场景三的应用，重点推导这两种场景下理想变压器的变比。

2.2 场景二的推导

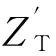
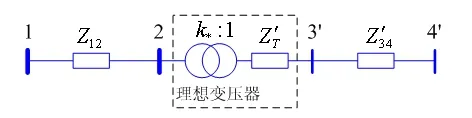
图4 场景二示意图

为了让学生理解场景二中k*的取值，首先引入以下电路帮助学生理解电压等级归算的效果。

假设变压器运行于主分接头(即有k=kN)，则图2所示电网归算到高压侧的等值电路如图5所示。

图5 按kN归算到高压侧的等值电路

对照图4和图5可以发现，当k=kN时，则图4中理想变压器变比k*=1，因此可以推测场景二中理想变压器的变比应为

k*=k/kN

(1)

下面，推导k≠kN的一般情况。显然，图5中节点4和4′的电压满足以下关系：

U4′=kNU4

(2)

即图5可以进一步表示为图6：

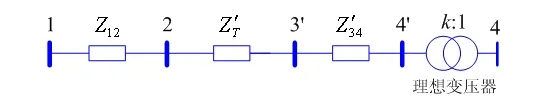
图6 按kN归算到高压侧的等值电路(接入理想变压器)

对照图2和图6可以发现，电压归算的效果就相当于移动理想变压器的位置，同时将理想变压器移动过程中所经过的阻抗均进行电压归算。

根据理想变压器的特性，图2中的理想变压器可以拆分为如图7所示的两台理想变压器，且变比满足

(3)

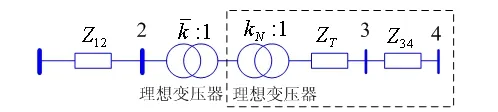
图7 含两台理想变压器的等值电路

对图7虚框部分进行电压等级归算(如图8)，相当于移动理想变压器(变比kN)的位置。

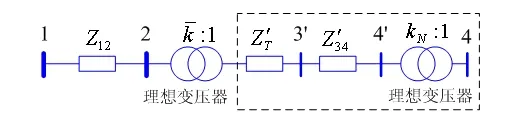
图8 按kN进行电压等级归算的等值电路

图8与图4完全等值，两种情况下理想变压器的变比取值相同，即：

(4)

由此可得场景二中理想变压器的变比应为

(5)

2.3 场景三的推导

仍然以图1所示简单电网为例。场景三的计算条件如图9所示。

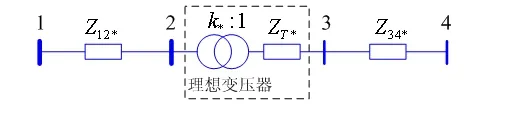
图9 场景三示意图

图中，Z12*为Z12按U1B和SB折算得到的标幺值；ZT和Z34分别为ZT和Z34按U2B和SB折算得到的标幺值，即：

(6)

(7)

(8)

可见，场景三实际上要解决的问题就是如何应用变压器П形模型建立全网的标么值等值电路，其关键同样是如何确定理想变压器变比k*的取值。

实际应用中，一般选取两级电网的额定电压或平均额定电压作为U1B和U2B。由于不要求U1B和U2B之间满足电压归算关系，且线路参数的标幺化在各自的电压等级完成，因此，场景三也称为建立电网标幺值等值电路的“就地标幺法”。

以下，基于“线路阻抗有名值恒定”原则推导图9中k*的取值。图9中，线路3-4的有名值阻抗为

(9)

设变压器的实际变比为k，则Z34归算到高压侧的有名值应为

(10)

若将图9中的Z34按k归算到高压侧，则有

(11)

进一步折算为有名值，有

(12)

显然，不论是按有名值还是按标幺值进行电压等级归算，两种情况下，线路阻抗归算到高压侧的有名值应相等，即：

(13)

联立式(9)～(13)，有

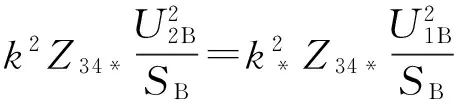
(14)

整理可得场景三中理想变压器的变比：

(15)

3 结语

变压器П形模型是“电力系统稳态分析”课程的一个难点。

(赵 霞等文)

现有教材大多只详细阐述了变压器П形模型的推导过程以及第一种应用场景，而对另外两种场景的分析和讨论都不够充分。

针对这一问题，本文以一个简单的4节点系统为例，详细讨论了另外两种场景下变压器П形模型的应用。通过理想变压器的拆分和移动推导了场景二中理想变压器的变比；基于“线路阻抗有名值恒定”原则推导了场景三中理想变压器的变比。从本文的分析和推导可见，三种应用场景下，变压器的建模原理相同，其关键都在于如何根据具体场景的已知条件确定П形模型中理想变压器的变比以及串联阻抗的数值。

本文所述方法已应用于我校“电力系统稳态分析”课程中变压器П形模型的教学实践，并取得了良好教学效果。

[1] 陈珩主编.电力系统稳态分析(第四版)[M]. 北京: 中国电力出版社, 2015年10月.

[2] 韩祯祥主编.电力系统分析(第五版)[M]. 杭州：浙江大学出版社, 2011年2月.

Instructional Practice of Transformer П Model

ZHAO Xia, LUO Lan, YU Lu-lu, LI Xin-yi

(SchoolofElectricalEngineering,ChongqingUniversity,Chongqing400044China)

Transformer П model is a difficulty point in the course Steady-State Analysis of Power System. According to the practical demands of power system modeling, there are mainly three application scenarios of the П model. Most textbooks only discuss the derivation process and the first application scenario of the П model in detail, while the other two scenarios are not analyzed thoroughly. This article focuses on the application of the transformer П model under the other two scenarios, and the ideal transformer ratios under individual scenario are derived in detail.

power system analysis; transformer П model; model derivation

2016-03-30;

2016-07- 19

赵 霞(1975-)，女，博士，副教授，主要从事电力系统分析教学、电力系统优化运行与风险评估的研究工作，E-mail：zx@cqu.edu.cn

G426

A

1008-0686(2017)01-0092-04