“电磁场与电磁波”课程中的计算思维培养

任宇辉， 高宝建

(西北大学 信息科学与技术学院， 陕西 西安 710127)

“电磁场与电磁波”课程中的计算思维培养

任宇辉， 高宝建

(西北大学 信息科学与技术学院， 陕西 西安 710127)

本文以“电磁场与电磁波”课程的教学为平台，在传统教学方法和内容改革的基础上，提出了基于计算思维的教学理念的改革思路。希望采用计算思维的方法，将本课程中的具体知识抽象成多种思维方式，进而丰富教学手段，提高教学质量。同时也希望通过对本课程的学习，能够加强对学生计算思维能力的培养，从而提高学习效率，解决具体问题。

电磁场与电磁波；计算思维；教学改革

0 引言

“电磁场与电磁波”课程(下文中简称“课程”)历来都是高等院校相关专业学生必修的基础平台课。由于该课程自身的特点和目前教学工作中存在的不足之处，该课程被公认为是一门“难教”、“难学”的课程。如何使这门课程的教学，既能体现培养目标的要求，又能适应科技的迅猛发展；既能在计划学时内完成教学任务，又能保证较高的教学质量和良好的教学效果，唯一的办法就是进行教学改革。

本文在传统教学方法和教学内容改革的基础上，提出了基于计算思维的教学理念的改革，主要工作包括：①采用计算思维的方法，对课程的教学内容进行梳理，将具体的知识抽象成多种思维方式；②通过实例说明如何将这些思维方式渗透到课程教学中去，从而改革教学理念，提高教学质量。

1 计算思维

1.1 计算思维的概念

计算思维的培养是美国卡内基梅隆大学计算机科学系主任周以真(Jeannette M. Wing)教授在2006年提出的教育理念[1]，指的是运用计算机科学的基础概念去求解问题、设计系统和理解人类的行为，包括了涵盖计算机科学之广度的一系列思维活动。

计算思维的理念一经提出就引起了国内外科学界和教育界的广泛关注，被认为是近十年来产生的最具基础性、长期性的思想[2]。中科院李国杰院士认为计算思维的培育是克服计算机科学“狭义工具论”的有效途径，是解决其他信息科技难题的基础[3]。文献[4]和文献[5]分别探讨了如何在程序设计和离散数学课程中强化学生的计算思维能力。

周以真教授还强调：计算思维不仅仅属于计算机科学家，还应该和阅读、写作和算术一样，成为21世纪每个人必须具备的基本技能。

1.2 计算思维的方法和特征

究竟什么是“计算思维”？目前为止，这在学术界还没有统一的共识[6]，每位学者对计算思维都有自己独到的见解。而周教授应该是对计算思维定义得最明确的一位。她在给出计算思维清晰定义的同时，还对其具体方法进行如下的详细描述：

(1)计算思维就是通过约简、嵌入、转化和仿真等方法，把一个看来困难的问题阐释成一个我们知道怎样解决的问题；

(2)计算思维是一种递归思维，是并行处理；

(3)计算思维采用了抽象和分解来迎接庞杂的任务或者设计巨大复杂的系统。它是基于关注点分离的方法；

(4)计算思维是按照预防、保护及通过冗余、容错、纠错的方式从最坏情形恢复的一种思维；

(5)计算思维利用启发式推理来寻求解答，就是在不确定情况下的规划、学习和调度；

(6)计算思维利用海量数据来加快计算，在时间和空间之间，在处理能力和存储容量之间进行权衡。

另外，周教授还总结了计算思维的几个特征：是概念化的，而不是程序化；是根本的，而不是刻板的技能；是人的，而不是计算机的思维方式；数学和工程思维的互补与融合；是思想，而不是人造物；面向所有的人，所有地方。

2 课程特点和当前教改中的问题

总结起来，“电磁场与电磁波”课程具有以下几个特点：

(1)课程体系庞大，涉及知识面广。该课程的学习，要求必须先完成“高等数学”、“大学物理”及“电路分析”等基础课程的学习，同时该课程还是“微波技术与天线”、“高等电磁理论”及“射频电路”等后续专业课程学习的基础。

(2)课程理论性强，概念抽象，数学公式繁多。电磁场看不见，也摸不着，故其涉及的概念和理论大都十分抽象，而且电磁场分布的计算还涉及到大量繁杂的数学公式和推导过程。

(3)课程的讲授，要求授课教师有很高的综合素质。既要有扎实的理论功底，又要有丰富的实践经验；既能够提炼出精彩的授课内容，又能创造出丰富的教学手段；既能传授基本的电磁理论知识，又能培养科学的思维方式，比如抽象思维、创新思维等。

除了课程自身的特点，其他一些主客观原因造成该课程的教学还存在以下几个问题：

(1) 电磁场与电磁波技术的应用发展迅速，但课程内容相对陈旧，教材的建设落后于技术的发展。尤其是目前绝大多数教材缺乏相应的应用背景的介绍，理论和应用脱节。

(2)实验与教学内容和进度不匹配，多数综合性院校缺乏开设电磁场实验的条件(主要原因是仪器较贵)，理论与实践脱节；

(3)随着近几年的课程改革，该课程的课时被大幅压缩，教学自由度受到很大限制。

结合以上特点，近年来众多学者关于“电磁场与电磁波” 课程做了大量教学改革工作。我们对其进行梳理，总结出目前的教学改革主要有两种思路：

其一是教学内容的改革。比如，本课程静态场部分和“大学物理”电磁学的内容大量重复，因此教学中，完全可以大幅度地压缩静态场的教学课时。这样既可以节约课时，增加教师教学的灵活性，又能避免重复，提高学生的学习兴趣，同时还能突出时变电磁场及其各种应用的重要性。

其二是教学方法的改进。主要是加强课件、动画及互联网等多媒体手段的开发、运用。合理、充分地利用各种多媒体教学手段，有助于提高教学效率，增强教学效果。

以上两个方面的教改工作，确实提高了学生学习的兴趣，提高了教学的效率和质量。但是我们也发现，这些改革的思路都只是表面上、形式上的。作为一门基础平台课，本课程蕴涵了丰富的科学思维方式和方法论。在课程教改的过程中，我们不能只停留于表面上、形式上的工作，而是应该更深层次地挖掘课程中蕴涵的科学思维方式和方法论，实现教学理念上的改革。

3 课程中的计算思维案例

前文提到“计算思维采用了抽象和分解来迎接庞杂的任务或者设计巨大复杂的系统，即选择合适的方式去陈述一个问题，或者选择合适的方式对一个问题的相关方面建模使其易于处理”。下面我们对课程中的具体内容进行抽象、总结。具体而言，就是探讨如何采用计算思维的方法，将大量具体的知识抽象成一种思维，进而再由思维来促进“知识”的掌握，最终提高学生的综合能力。

3.1 将具体知识抽象到通用平台的思维

麦克斯韦(Maxwell)方程组是一切宏观电磁现象满足的基本规律，其一般形式可表示为

(1)

一般教学过程中，我们注重讲授方程相关定理的证明、意义及应用背景等。但是，如果我们采用计算思维对这部分知识进行抽象，则可以发现Maxwell方程组的推导、分析和求解贯穿于我们教学的始终，可以说该方程组是本课程的一个通用平台。

比如我们可以从电磁学发展的历史，抽象出Maxwell方程组中蕴含的“对称性思想”：电磁学发展的历史上，第一次把电、磁联系起来的是丹麦学者奥斯特(Oersted)在1820年的实验，他发现电流可以影响邻近的磁针转向。根据对称性思想，英国物理学家法拉第(Faraday)坚持认为既然“电能生磁”，那么一定也存在“磁能生电”。所以他坚持十年(1821～1831)不懈努力，终于发现了电磁感应定律。其实法拉第的研究结果和最初的设想并不完全相同，原来设想的是既然“电流能够产生磁场”，那么对称的结果应该是“磁流能够产生电场”。然而最终的结果却证明了“变化的磁场能够产生电场”。后来英国物理学家Maxwell也自觉接受了对称性思想的指导，在前人工作的基础上，通过理论推导提出了变化的电场，即位移电流也可以产生磁场。需要说明的是，基于对称性的思维人们到现在为止也一直在寻找“磁流”的存在，但却一直没有结果。

在教学过程中，我们以电磁学发展的历史为背景，以对称性思想为主线，抽象甚至假想出方程中的对称性关系(见表1)，显然可以使我们的教学更加生动、高效。

以此类推，还可以将电磁波在不同边界媒质中的传播特性，抽象成Maxwell方程组在不同边界下的解；应用微积分的思想，将电磁场的边界条件抽象成Maxwell方程组在不同媒质分界面上的表现形式；将波动方程的推导抽象成Maxwell方程中二元一次方程组的求解；将电磁波产生的条件抽象成Maxwell方程组中蕴涵的时空变换、电磁转换等等。

表1 Maxwell方程组中的对称性关系

3.2 从多门课程抽象、凝练出共性的思维

前文提到“电磁场与电磁波”是一门基础平台课，具有很宽的知识面，很强的综合性。另外，计算思维的方法也应该是蕴涵于多门课程之中的。所以在教学时，我们应该引导学生去寻求本课程和其它课程的共性，力求做到举一反三。

在讲授时谐场及其满足的Maxwell方程组时，我们经常要用到场的复数表示，比如电场强度的复数表示：

(2)

第一方程的复数形式

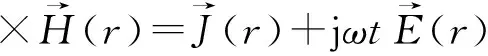
(3)

式中r代表空间坐标的参数，在不同的坐标系中有不同的形式。对式(2)式的理解，我们可以认为这是将瞬时值表示的电场(时域信号)展开成傅里叶级数，表示成了频域信号。式(3)我们则可以理解为将式(1)中的瞬时形式的Maxwell第一方程通过傅里叶变换转换成了频域形式。这种变换可以大大简化分析和运算，因为①时域中的场既是空间的函数又是时间的函数，频域则只是空间的函数；②时域方程中关于时间的偏微分的运算变成了频域中的代数运算。

显然，在讲授这部分知识的时候，我们可以发现它和“信号与系统”课程中频域分析法的共性。我们可以对这部分内容进行抽象、凝炼，得出适用于多门课程的频域分析思维。

3.3 将不同知识联系起来的贯通性思维

传统的“电磁场与电磁波”的教学，容易使学生形成以下几个方面的思维上的对立：

(1)“场”和“路”的对立。在教学中，我们经常会对学生说低频电子线路属于集中参数系统，它的分析要用到以基尔霍夫定律为核心的“路”的方法。而射频及微波电路属于分布参数系统，对其分析要用到以Maxwell方程组为基础的“场”的理论。所以初学者往往会认为这是两套相互独立的知识体系。相对而言，“路”更加具体，更加容易理解，因此大多数学生会对场的理论敬而远之，甚至产生抵触。

(2)时变场和静态场的对立。目前大多数“电磁场与电磁波”课程内容的安排都是先讲静态场(静电场、恒定电场和恒定磁场)的概念、性质及其满足的基本方程等，然后再来介绍时变场，进而总结出Maxwell方程组。这样的安排固然满足由浅入深的规律，但也无意间将静态场和时变场对立了起来。

(3)自由空间场和介质中场的对立。同样是出于由易到难的考虑，我们习惯上在授课时先介绍自由空间(μ0,ε0)中场的性质，然后再将其推广到媒质中去(μ=μ0,μr,ε=ε0εr)。这又将自由空间场和介质中场对立成两个体系。

但只要我们能对以上知识加以融会贯通，就能抽象出蕴涵其中的贯通性思维：

(1)“场”和“路”是统一、不可分割的[8]。“场论”适用于一切宏观电磁现象，“路论”是其在直流和低频情况下的特例。表2呈现了两种理论的一致性关系。

(2)静态场和时变场也是统一的。静态场是时变场在满足下式所示条件下的特例。

(4)

(3)介质中场和自由空间场的特点完全相同，只要满足μr=1,εr=1即可。

总之，只要我们采用计算思维的方法，积极将不同方面的知识联系起来，打通知识间的屏障(如术语上的差异等)，就能大大促进我们的教学。

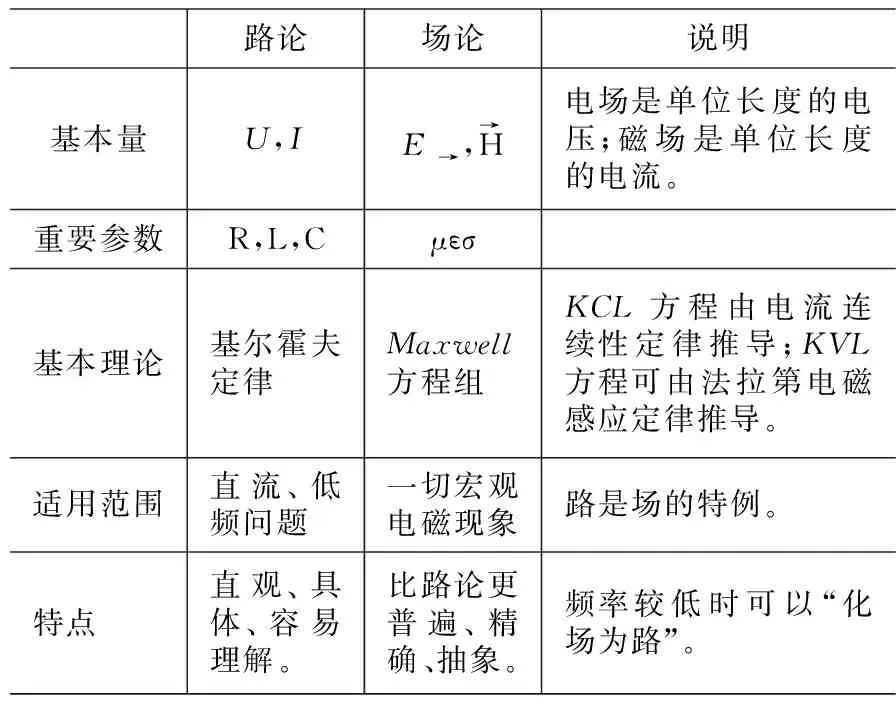
表2 “路论”和“场论”中的一致性关系对比

4 结语

本文提出了一种基于计算思维的教学理念的改革。这种改革不是对以前教学改革工作的否定，而是从思维方式和方法论的角度对其进一步地深化：将计算思维应用于“电磁场与电磁波”课程的教学工作中，无疑是教学方法的重要改革。同时我们要将课程中具体的内容抽象成某种思维方法，要将本课程的内容和其他相关课程建立联系使其系统化，这显然也是教学内容的改革。通过这项改革，我们希望：①在课程教学中引入计算思维，改进教学方法，丰富教学手段，进而提高教学质量；②可以加强对计算思维能力的培养，使学生能够更好地应用计算思维来提高学习效率，解决具体问题。

[1] Jeannette M. Wing. Computational Thinking [J]. New York:Communications of the ACM, 2006,49(3):33-35.

[2] 孙家广,计算机科学的变革[J]. 北京：中国计算机学会通讯,2009,5(2): 6-9.

[3] 中国科学院信息领域战略研究组.中国至2050年信息科技发展路线图[M].北京：科学出版社，2009.

[4] 陈杰华,程序设计课程中强化计算思维训练的实践探索[J]. 北京：计算机教育,2009(20):84-85.

[5] 常亮，徐周波. 离散数学教学中的计算思维培养[J]. 北京：计算机教育，2011(14):90-94.

[6] 牟琴,谭良.计算思维的研究及其进展[J]. 重庆：计算机科学,2011,38(3):10-15.

[7] 梁昌洪,关于电磁理论的若干思考[J].南京：电气电子教学学报, 2004,26(1:)1-15.

[8] 丁君.工程电磁场与电磁波[M].北京:高等教育出版社,2005.

The Building of Computational Thinking in Electromagnetic Field & Wave Course

REN Yu-hui, GAO Bao-jian

(SchoolofInformationScienceandTechnology,NorthwestUniversity,Xi′an710127，China)

This paper, taking the teaching of the Electromagnetic Field and Wave course as the platform, based on the reform of the methods and the contents for traditional teaching, put forward the ideas of teaching reform based on computational thinking. By the way of computational thinking，specific knowledge in the course is abstracted to a variety of ways of thinking , then the teaching methods are enriched and the teaching quality is increased. Through the study of this course, the development of computational thinking ability for students, as well as the improvement of their learning efficiency and the ability of solving problems, are expected.

electromagnetic field and wave; computational thinking; teaching reform

2016-01-04;

2016-05-03 基金项目：西北大学本科教学质量与教学改革工程项目(No.JX14035).

任宇辉(1980-)，男，博士，讲师，主要从事电磁场与电磁波、微波技术与天线等教学、科研工作，E-mail：ryhui13579@163.com

G642.0

A

1008-0686(2017)01-0025-04