汽油馏分烃化合物组分的蒸气压计算

焦国凤，周 祥，孟繁磊，于 博

(中国石化石油化工科学研究院，北京 100083)

汽油馏分烃化合物组分的蒸气压计算

焦国凤，周 祥，孟繁磊，于 博

(中国石化石油化工科学研究院，北京 100083)

应用立方型状态方程计算气液相平衡，求取汽油馏分中烃化合物组分在任意指定温度下的饱和蒸气压，为汽油馏分的气液相平衡计算提供支持。方程求解通过编程实现，输入参数包括化合物的临界温度、临界压力和偏心因子，输出为对应温度下化合物的蒸气压。利用该方法可以计算汽油馏分中所包含的400多种烃化合物的蒸气压，比较了在37.8 ℃下的蒸气压计算值和实测值，结果吻合较好，轻烃化合物蒸气压的平均相对误差低于1%，汽油全馏分范围内烃化合物蒸气压的平均相对误差低于4%。

汽油馏分 烃类化合物 蒸气压计算 状态方程

蒸气压是化合物重要的热力学性质之一，是指在一定温度下该物质的气液两相处于平衡状态时的气相压力，用于衡量流体的蒸发性能。通常，化合物的蒸发趋势越大，蒸气压越大；蒸发性大的物质临界压力大，临界温度低，密度小，沸点低，也称为轻组分，反之为重组分。在炼油装置的安全、设计以及操作等相关计算中都需要蒸气压值。例如，烃蒸发损失以及烃蒸气在空气中的着火点等均与烃分子的蒸气压有关。挥发性高的丁烷掺入汽油中可以提高汽油的点火性能，而挥发性低的化合物可以减少蒸发损失和降低气阻形成的倾向，所以燃料油的组分构成是轻、重组分含量的优化结果[1-2]；在化工过程的相平衡计算中，蒸气压可以用于平衡常数的计算；雷德蒸气压(RVP)是汽油重要的质量标准之一，可以由其各组分的蒸气压来计算。

纯烃化合物在不同温度下的蒸气压可以通过实验测定，在TRC热力学性质表中收集了部分实测数据，在API-TDP中也用图线方式表示出一些烃类和非烃类化合物蒸气压与温度的对应关系[3]。文献中纯烃化合物蒸气压的计算方法大体分两类：一类是蒸气压与温度的直接经验关联式，另一类是普遍化关联式。如Antoine方程、Daubert方程[3]这类直接经验关联式中一般包含3～5个关联常数，而且关联常数与烃分子一一对应，Aspen计算软件采用该类关联式计算化合物蒸气压；通用关联式是更实用的预测方法，即只需要化合物的基础性质如沸点等，简单形式如van-van关联式[4]，复杂形式如Maxwell-Bonnel关联式[5]，如果纯物质的临界性质如临界温度Tc、临界压力pc和偏心因子ω可以得到，也可以采用更详细的关联模型，如Lee-Kesler关联式等[6]。上述关联式都可以用来计算烃化合物的蒸气压，但是在实际应用中，一方面可得到的资源不一定能够满足对公式中关联常数的需求，另一方面多数关联式的适用温度范围受限，从而影响计算精度。本研究采用求解立方型状态方程的方法来计算烃化合物的蒸气压，减少对关联参数的依赖，从而满足更广泛的需求。

1 汽油馏分分子组成模型的建立

汽油馏分分子组成模型是构建分子水平过程动力学模型的基础步骤，在过程模型中对原料和产物进行物性表征必不可少，因此为汽油馏分中的烃化合物提供蒸气压值是过程动力学模型的基础组成部分。

依据石脑油、催化裂化汽油等样品的详细烃分析数据以及己经建立的石油烃类化合物分类方法[7]，结合各种化合物的反应性能，为汽油馏分建立了分子组成模型。石脑油和重整油分子组成模型中包含200余种单体烃化合物，催化裂化汽油组成模型中包含300余种单体烃化合物，两类模型中烃化合物总数达400余种。如果利用前已述及的关联式计算这些烃化合物的蒸气压值，比如常用的Antoine方程：

(1)

式中：A～E均为与烃分子自身一一对应的关联常数；p、T分别为对应的温度和压力。其它关联式如Daubert方程：

(2)

式中：a～d为组分关联常数；pr、Tr分别为对比压力(ppc)和对比温度(TTc)，τ=1-Tr。上述关联常数在文献中仅能提供部分化合物的数据，因此数量上未能满足需要；如果采用如下的Lee-Kesler普通化关联式[6]：

(3)

式中，ω为偏心因子，尽管使用方便，但是式中的关联系数或许会限制关联式的使用温度范围。以下将解析如何采用求解状态方程的方法预测汽油馏分中烃化合物的蒸气压。

2 汽油分子模型中烃化合物蒸气压的计算

2.1 立方型状态方程

作为一种描述流体p-V-T行为的模型，立方型状态方程既可以同时计算液相和气相的性质，又可以包含较宽的温度和压力范围。在工程界相平衡计算中，SRK方程和PR方程被广泛接受并经常使用。SRK状态方程基本形式及计算式如下[8]：

(4)

a=acα

(5)

(6)

α=(1+fω(1-Tr))2

(7)

fω=0.48+1.574ω-0.176ω2

(8)

(9)

PR状态方程基本形式及计算式如下[9]：

(10)

a=acα，

(11)

α=[1+fω(1-Tr)]2

(12)

fω=0.374 64+1.542 26ω-0.269 92ω2

(13)

(14)

两方程中都包含了参数a、b，每种物质都有自己的一对参数，其中参数b与物质的临界性质Tc、pc有关，在两方程中参数b的表达式相同；参数a还考虑了T和ω的影响，在两方程中的表达式略有区别，PR方程中a对体积的表达更精细，使得其预测液体摩尔体积的准确度较SRK方程有明显改善，两者都可用于描述极性物质。

2.2 烃分子蒸气压的求解

立方型状态方程是关于摩尔体积的三次方，故解方程可以直接求得气、液两相的摩尔体积。为方便求解，将V，a，b分别无因次化为Z，A，B，如下所示：

(15)

当气、液两相处于平衡状态时，气相、液相的逸度f相等，由于两相压力也相等，因此又可以认为逸度系数φ相等。利用上述无因次变量可以表示逸度系数，两方程中φ的计算式分别如下[1]：

(16)

(17)

式(16)用于SRK方程，式(17)用于PR方程。

以SRK方程为例，说明由纯烃化合物的临界性质Tc，pc，ω计算在任意温度T下蒸气压p的计算过程。步骤如下：①输入已知量：Tc，pc，ω和T，利用式(5)～式(9)计算状态方程参数a、b；②计算无因次参数A、B：据蒸气压p的假设值，利用式(15)计算A、B；③计算压缩因子：假定摩尔体积的初值，利用迭代法求解气、液相的摩尔体积V，并计算Z值；④计算逸度系数：利用式(16)分别计算气、液相的逸度系数φv和φl；⑤判断蒸气压的假设值是否合理：定义一个计算终止的误差判断式ε=|φl-φv|，当误差值小于一个设定的小值，则认为计算可以终止，此时的p值为最终的计算值；如果不满足该条件，则调整p值，重复步骤②～⑤，继续迭代，直至满足要求为止。PR方程的求解过程与SRK方程类似，这里不再赘述。上述求解过程通过编程实现。

3 结果与讨论

针对第1节所建立的汽油组分分子模型中的化合物，通过查阅数据库和计算的方法得到全部化合物的临界性质Tc，Pc，ω，将其作为蒸气压计算程序的输入参数。求解立方型状态方程，计算400多种烃化合物在任意温度下的蒸气压值，状态方程可以在SRK方程和PR方程之间切换选择。以下通过对计算值与实测值的对比来考察各种计算方法的精度和可靠性。

3.1 状态方程法与普遍化关联法的比较

部分烃化合物在37.8 ℃下蒸气压的计算值与实验值的对比结果如图1～图5所示。计算方法包括SRK方程、PR方程以及前述Lee-Kesler通用关联式。化合物的碳数范围是C3～C10。化合物种类覆盖了汽油组分所含全部化合物类型，包括正、异构烷烃，正、异构烯烃，单取代基和多取代基的环烷烃和芳烃。蒸气压数值范围为0.5～500 kPa。由于在整个汽油馏程内所涉及的蒸气压范围较宽，所以如图1～图5分段显示。

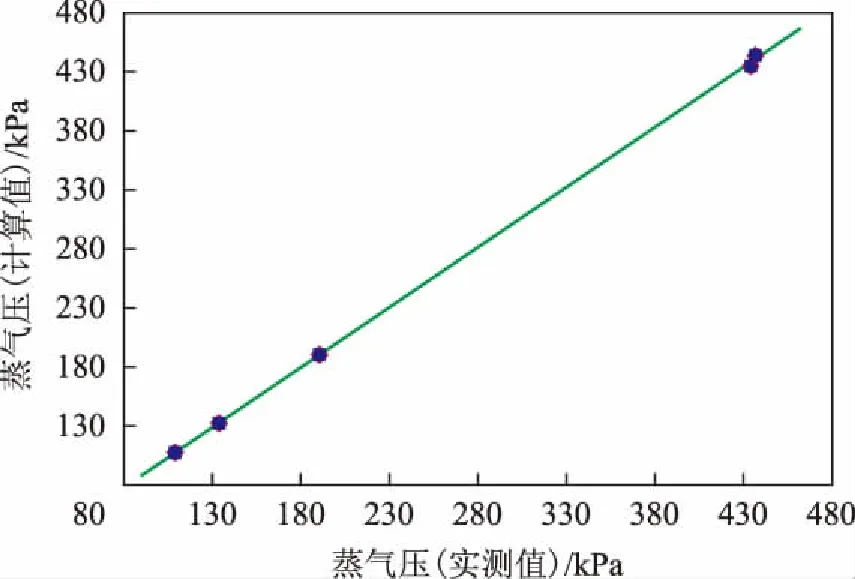
图1 C4～C5烃蒸气压计算值与实测值比较◆—Lee-Kesler； ■—PR； ●—SRK。 图2～图5同

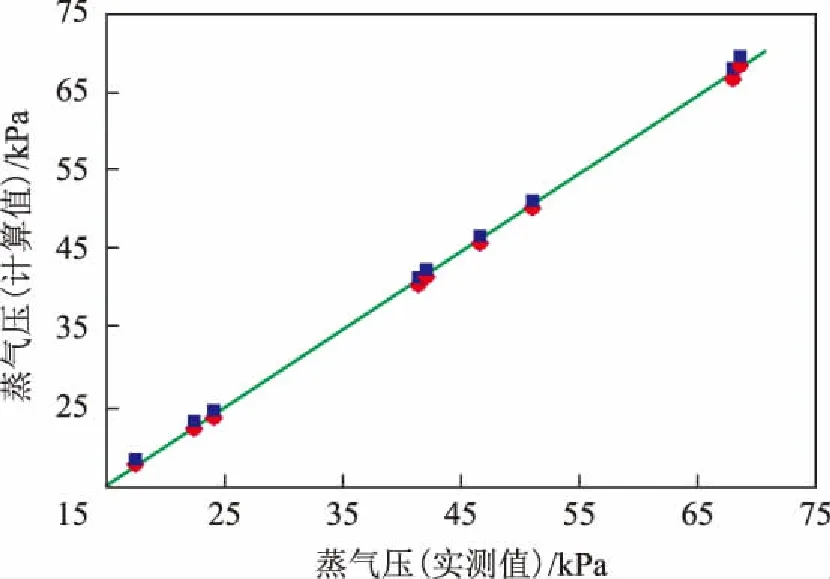
图2 C5～C6烃蒸气压计算值与实测值比较

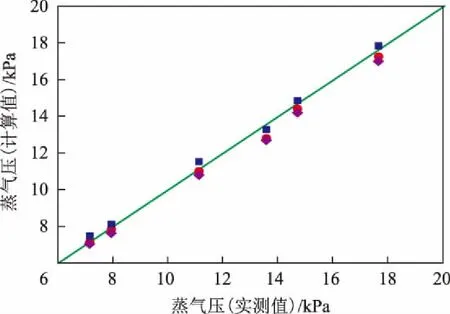
图3 C7烃蒸气压计算值与实测值比较

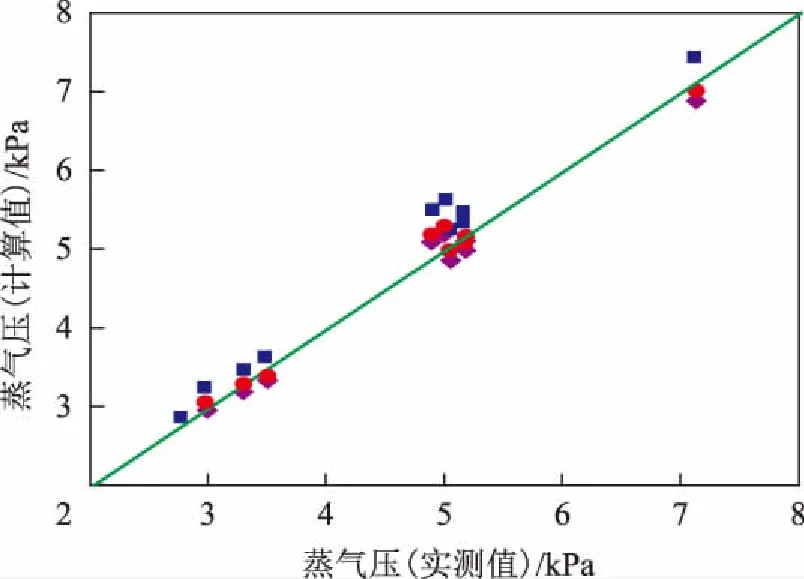
图4 C8烃蒸气压计算值与实测值比较

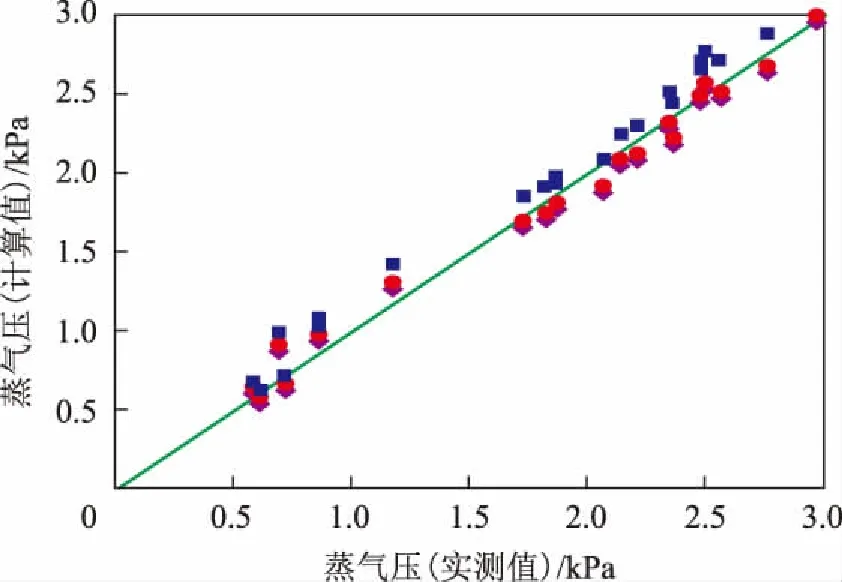
图5 C8～C10烃蒸气压计算值与实测值比较

图1表示了C4～C5烯烃组分的蒸气压，数值在100～500 kPa之间，3种方法的预测精度均较好，平均相对误差约为0.5%左右。图2表示了C5～C6烃化合物的蒸气压，数值在20～80 kPa之间，3种方法的平均相对误差在1%左右，其中SRK方法比另外两者的预测精度更好，误差约为0.7%。图3表示了C7烃化合物的蒸气压，数值在7～20 kPa之间，3种方法的平均相对误差在2.5%左右，其中SRK方程的预测精度较好，误差约为2%，Lee-Kesler关联式的误差较大，约为3.7%。图4表示了C8烷烃化合物的蒸气压，数值在2～6 kPa之间，其中SRK方程的预测精度最好，误差约为2.5%，PR方程预测精度偏低，误差达6.7%。图5表示了C8～C10烷烃和芳烃类化合物的蒸气压，数值较小，在0.3～2 kPa之间，相比之下PR方程关联式的误差偏大，约为7%左右。

由上述分析结果可见，用3种方法预测低碳轻烃的蒸气压值均较可靠；在汽油全部馏程范围内，SRK方程预测效果最好，平均误差低于4%，Lee-Kesler关联式次之，误差低于6%，PR方程平均预测精度低于前两种方法，误差达7%。尽管PR方程预测液体摩尔体积的准确度较高，但是预测蒸气压未见优势。形式简单的Lee-Kesler式源自对三参数对应状态方程的关联，是计算气液相的p-V-T关系较准确的方法，也是API-TDB推荐的方法。

3.2 状态方程法与关联常数法的比较

分别采用SRK和PR两种状态方程以及前述Daubert方程、Antoine方程计算苯在127 ℃下的蒸气压。苯的关联常数可以从文献中查阅，式(3)的对比性质可以计算，将用4种方法得到的计算值与API的实测值进行比较，结果如表1所示。式(1)和Antoine方程2种关联常数法的计算误差分别为2.3%和2.1%，计算精度较好。关联常数通常是在指定的温度范围内回归得到，最理想的蒸气压关联式应该使该物质从三相点到临界点都有效，不过通常还没有关联式在这么宽的范围内都有效。通常在关联温度范围内关联式的计算精度较好，范围之外计算精度变差，而且不同来源的关联常数值可能也有差异，也是回归参数时的温度范围不同所致，通常温度越低，精度越高。这种方法简单方便，适合手工计算。表1中SRK和PR 2种状态方程法预测值误差分别为2%和1.4%，都很可靠，预测精度也很接近。由于可查到的蒸气压的实验值数量有限，不便进行对各计算方法适用温度范围的考察。

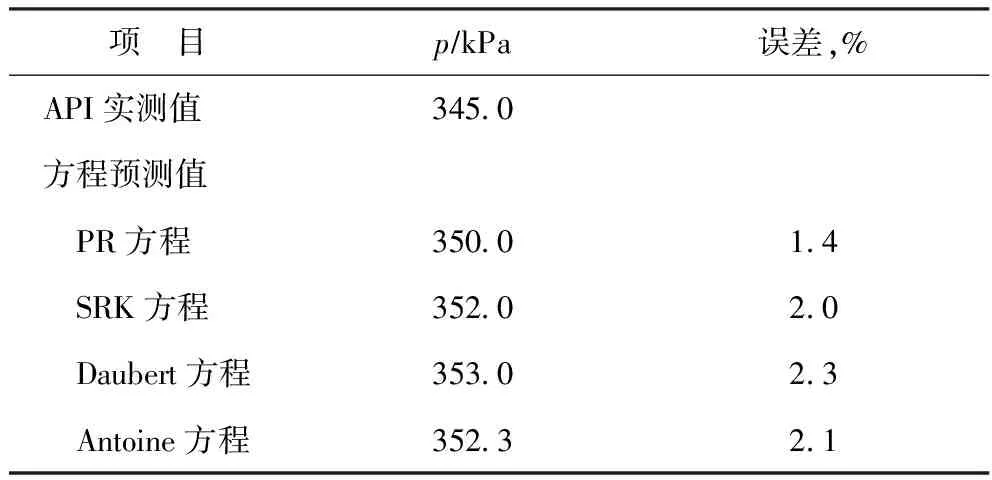
表1 苯在127 ℃蒸气压的几种预测值对比

4 结 论

应用SRK和PR 2种状态方程计算气液相平衡，建立了纯烃化合物在任意指定温度下蒸气压的计算方法。输入数据为化合物的3个临界参数Pc、Tc和ω，输出数据为对应温度下的蒸气压。求取了汽油馏分中所包含的近400种纯烃化合物的饱和蒸气压值。对37.8 ℃下蒸气压的计算值与实测值的比较结果表明：对于低碳烃化合物来说，这2种方程的蒸气压预测精度接近，平均相对误差均低于1%；而对于汽油全馏程组分化合物来说，SRK方程的预测精度高于PR方程。比较结果也表明：SRK方程的预测精度稍高于API推荐的Lee-Kesler关联式；另外，采用SRK方程法求取蒸气压的附加值更高，计算过程中可以获得摩尔体积、逸度等参数，从而根据需要还可以求解如熵、焓等其它热力学性质。因此，采用状态方程方法既可以保证化合物蒸气压的预测精度，同时也可用于预测其它热力学性质，具有更广泛的意义。

[1] 张玉瑞，陈微微，杜铭，等.调合汽油恩式蒸馏数据的预测模型[J].石油炼制与化工，2016，47(7)：38-42

[2] 刘倩，刘顺涛，郑煜.车用汽油驱动性指数研究[J].石油炼制与化工，2016，47(4)：96-100

[3] Riazi M R.Characterization and Properties of Petroleum Fractions[M].Philadelphia， USA：ASTM International，2005：238-305

[4] van Nes K，van Western H A.Aspects of the Constitution of Mineral Oils[M].Amsterdam：Elsevier，1951：104

[5] Maxwell J B，Bonnell L S.Deviation and precision of a new pressure correlation for petroleum hydrocarbons[J].Ind Eng Chem，1957，49：1187-1196

[6] Lee B I，Kelser M G.A generalization thermodynamic correlation based on three-parameter corresponding states[J].American Institute of Chemical Engineering Journal，1975，21：510-527

[7] 孟繁磊.石油中烃类化合物的结构分类与物性关联研究[D].北京：石油化工科学研究院，2010

[8] Soave G.Equilibrium constants from a modified Redlich-Kwong equation of state[J].Chem Eng Sci，1972，27：1197-1203

[9] Peng D Y，Robinson D B.A new two-constant equation of state[J].Industrial and Engineering Chemistry Fundamental，1976，15(1)：59-64

CALCULATION OF VAPOR PRESSURE OF PURE COMPOUNDS IN GASOLINE

Jiao Guofeng， Zhou Xiang， Meng Fanlei， Yu Bo

(SINOPECResearchInstituteofPetroleumProcessing，Beijing100083)

The cubic equation of state was used to predict the vapor pressure of pure compounds at the specified temperature at which vapor-liquid equilibrium occurred. The equation of state was solved using the programs， in which the vapor pressure was reported when the critical properties as the critical pressure， critical temperature and acentric factor were specified. The vapor pressures of more than 400 compounds in gasoline were calculated by SRK or PR EOS. The predictions of vapor pressure of some hydrocarbon compounds at 37.8 ℃ are in good agreement with the observations. The average relative error is lower than 1% for the light compounds， and lower than 4% for all the compounds in full range gasoline.

gasoline fraction； pure hydrocarbon； vapor pressure calculation； EOS

20116-04-22； 修改稿收到日期： 2016-08-15。

焦国凤，博士，高级工程师，主要从事分子水平炼油过程模型的研究工作。

焦国凤，E-mail： jiaogf.ripp@sinopec.com。

中国石油化工股份有限公司合同项目(115037)。