电杆钢筋结构对塔顶电位的影响

苑维琦，魏 宁，孙振勇，史蕾玚，刘永亮

（国网山东省电力公司青岛供电公司，山东 青岛 266002）

电杆钢筋结构对塔顶电位的影响

苑维琦，魏 宁，孙振勇，史蕾玚，刘永亮

（国网山东省电力公司青岛供电公司，山东 青岛 266002）

在分析输电线路防雷水平时，除了要考虑钢筋混凝土电杆的冲击接地电阻，还应考虑其钢筋结构的影响。为分析输电线路钢筋混凝土电杆钢筋结构对其塔顶电位的影响，利用电力系统接地分析软件CDEGS搭建10 kV输电线路钢筋混凝土电杆模型，计算在不同波形雷电流作用下电杆的塔顶电位。仿真结果证明，混凝土电杆塔顶电位与雷电流波形有关，通过进一步计算对比电杆钢筋结构和接地极的阻值，分析得到在不同雷电流波形作用下，当塔顶电位达到最大值时，电杆钢筋结构阻抗差别明显，在造成电杆塔顶电位差异的过程中起到主要作用，雷电流波头时间越短，电杆钢筋结构感抗越大，对塔顶电位造成的影响越大。因此要提高输电线路的防雷水平，一方面应降低电杆的冲击接地电阻，还应改进电杆钢筋结构，以降低感抗作用的影响。

CDEGS软件；钢筋混凝土电杆；钢筋结构；雷电流；塔顶电位

0 引言

钢筋混凝土电杆在输电线路中应用非常广泛，它由地线支架穿钉通过内配钢筋连接到接地螺栓作为接地引线，由接地引下线焊接在接地体上［1］。当雷电冲击电流从塔顶经过钢筋结构注入接地极时，在雷电冲击电流的作用下电杆钢筋结构的阻抗会对塔顶电位造成影响。在以往对电杆冲击接地电阻的研究中［2-7］，多数只考虑电杆的接地极电阻，传统的接地电阻测量方法也将接地极电阻视为电杆的接地电阻［8］。但由于难以检查混凝土电杆接地引线是否可靠连接，故电杆接地引线导通性能较差 。因此对于输电线路防雷保护，传统的冲击接地电阻研究方法无法真正反映雷击时的塔顶电位，传统的接地电阻测量方法也不能保证电杆钢筋跟接地极有效连接［9-10］。为了客观准确地反映输电线路防雷害能力，除了考虑电杆的冲击接地电阻，还应考虑电杆钢筋结构对塔顶电位造成的影响。

为了研究电杆钢筋结构对其塔顶电位的影响，利用电力系统接地分析软件CDEGS建立典型的10 kV输电线路钢筋混凝土电杆模型，在不同波形雷电流作用下，计算电杆的塔顶电位，并分别计算得到电杆钢筋结构与接地极的阻值，从而可以较为准确地分析出电杆钢筋结构对塔顶电位的影响程度。

1 建立电杆模型

1.1 仿真电杆参数

仿真选取的研究对象为10 kV输电线路常用电杆，其型号为Φ190-15-J-G（非预应力），该电杆为15 m环形钢筋混凝土电杆，根径Φ390 mm，梢径Φ190 mm。主筋型号为14Φ14 mm，主筋保护层厚度15 mm。电杆结构示意图如图1所示，电杆钢筋结构尺寸见表1。

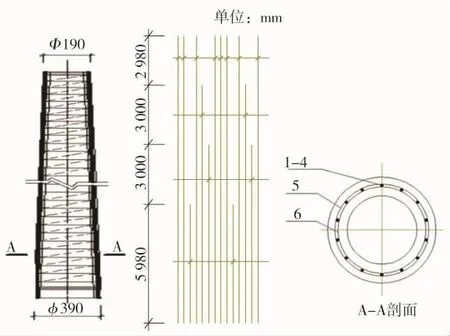
图1 电杆结构示意

表1 电杆钢筋结构尺寸

电杆钢筋材料相对磁导率μ0=6 000，相对电导率σ=8.0×105S·m-1。电杆埋深2.3 m，电杆周围土壤电阻率为20 Ω·m。

1.2 仿真计算原理

目前国内外文献提到的雷电冲击电流作用下电杆塔顶电位的积分表达式可以表示为［11］

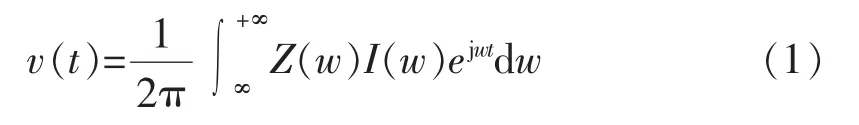
式中：Z（w）为调制电压，表示单位冲击电流作用下每个频率点对应的电压值；I（w）为雷电流频谱。

CDEGS是基于矩量法的电磁场数值分析软件，它能够将电场积分方程和磁场积分方程化为有限求和或差分方程，从而建立代数方程组，然后通过运算矩阵方程求解［12］。因此可以计算不同频点下单位激励源产生的电压，即Z（w）。

CDEGS软件适合于计算地上或地下任意位置带电导线组成的网状结构产生的导线电位、接地电位和电磁场。将电杆环形钢筋结构的栅格看作网状结构，通过两个端点的坐标、半径、分段数目定义每段导线，并以每段导线的轴向电流为变量，对每段导线列电场积分方程求解空间电磁场。

由于每段导线半径和长度远小于激励源波长，因此可以忽略每段导线电流的横向分量和环向分量，只考虑轴线方向的电流和强加电场边界条件。

由达朗贝尔方程

式中：

以及洛伦兹规范

得到导线空间一点电场强度E满足

式中：E为电场强度，v／m。A为导线轴向电流产生的矢量磁位；φ为导线表面线分布电荷产生的标量电位。在准静态场中：

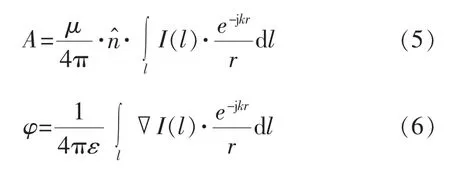
式中：r为源点到场点的距离，单位m；k为传播常数；I（l）为轴向电流。

将式（5）、（6）代入式（4）中，得到复数形式电场强度积分方程

用矩量法求解积分方程，每段导线上的电流基函数由常数、正弦、余弦线性组合而成，即表示为

对于每一段导线有A、B、C 3个未知系数，根据电流连续性方程和电荷密度条件可以消去2个未知数，则未知数与导体段数相同，通过矩量法求得I（l），进而可以得到Z（w）等未知量。

在CDEGS软件中，对雷电流进行快速傅里叶变换，从而由时域转换到频域进行分析。得到雷电流采样频率点之后，根据上述方法求取塔顶至接地极整段导体在采样频率点下的单位冲击阻抗频域值Z（w）。代入式（1）可以得到塔顶电位。

2 CDEGS仿真

对上述电杆进行现场实验，电杆埋深2.3 m，土壤电阻率为20 Ω·m。由塔顶注入8／22 μs实验雷电流波形，幅值为2.5 kA，测量电杆塔顶电位。并用CDEGS软件搭建电杆模型，模拟现场实验条件，计算电杆塔顶电位，并与实验测得的结果进行对比，如图2所示。

图2 实验与仿真结果对比

通过对比可知，CDEGS软件计算的塔顶电位与现场实验结果基本一致。验证了仿真模型的正确性。以该模型进行仿真，仿真过程中分别对钢筋混凝土电杆塔顶施加波形为2.6／50 μs，1／50 μs以及8／22 μs的雷电流，雷电流波形均使用双指数函数拟合［13-15］，雷电流的幅值均为1kA。3种雷电流波形如图3所示。

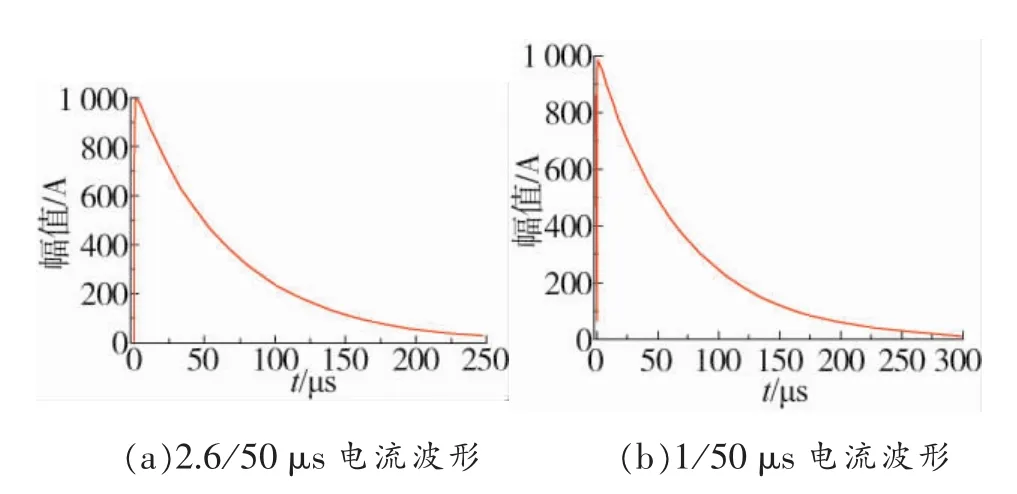
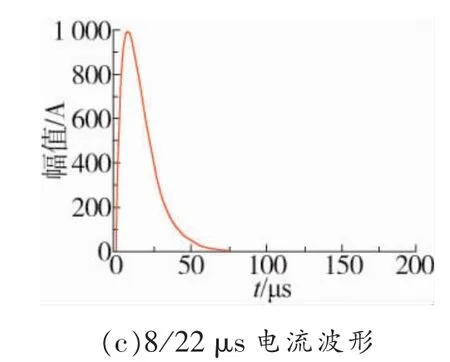
图3 雷电流波形

将上述3种雷电流分别作用于电杆钢筋结构顶部，使用CDEGS软件计算电杆塔顶电位，计算结果如图4所示。

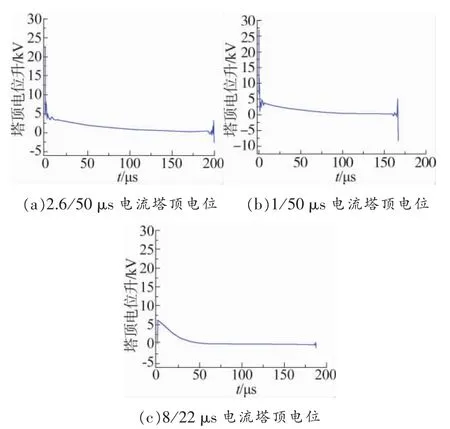
图4 塔顶电位

由图4可知，2.6／50 μs雷电流波形下电杆塔顶电位为23.9 kV，1／50 μs雷电流波形下电杆塔顶电位为26.kV，8／22 μs雷电流波形下电杆塔顶电位为6.5 kV。

计算结果说明，电杆塔顶电位受雷电流波形的影响。为了具体分析在3种情况下，电杆钢筋结构和接地极分别对塔顶电位的影响程度，分别计算了在3种雷电流作用下，当电杆塔顶电位达到最大值时，电杆钢筋结构电阻值、感抗值，接地极电阻值、感抗值。统计如表2～4所示。

由统计结果可知，在3种不同波形雷电流作用下，当塔顶电位达到最大值时，电杆接地极阻抗差别不明显，而钢筋结构阻抗差别明显。2.6／50 μs雷电流波形作用下钢筋结构阻抗为22.6 Ω、8／22 μs雷电流波形钢筋结构阻抗为4.13 Ω。对比这两种情况下的数据，两者的钢筋结构电阻都很小，当雷电流波形变化，钢筋结构电阻基本不变；两者钢筋结构感抗分别为22.6 Ω和4.13 Ω，随雷电流波形变化明显。因此可以说明，电杆钢筋结构感抗随雷电流波形变化显著，在不同波形雷电波下造成塔顶电位差别的主要原因是钢筋结构的感抗。

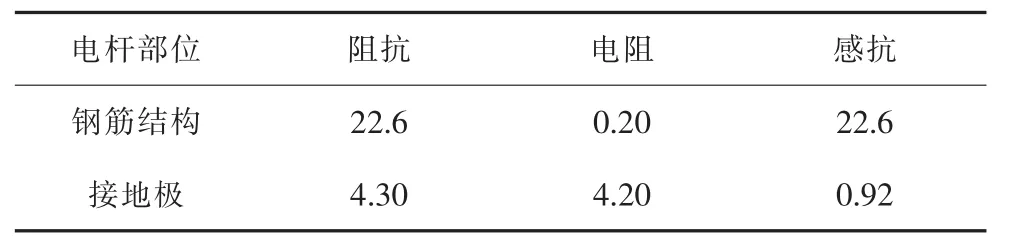
表2 2.6／50 μs雷电流下电杆各部分阻抗值 Ω

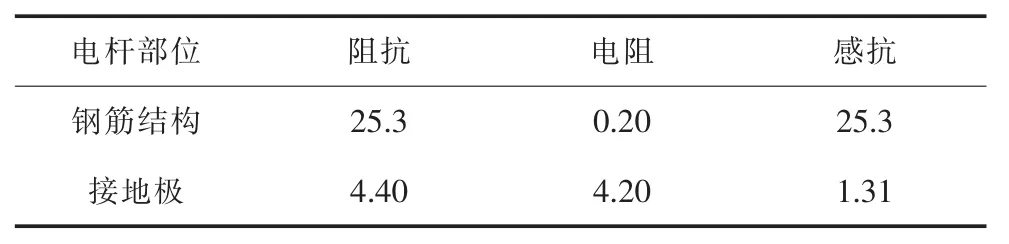
表3 1／50 μs雷电流下电杆各部分阻抗值 Ω

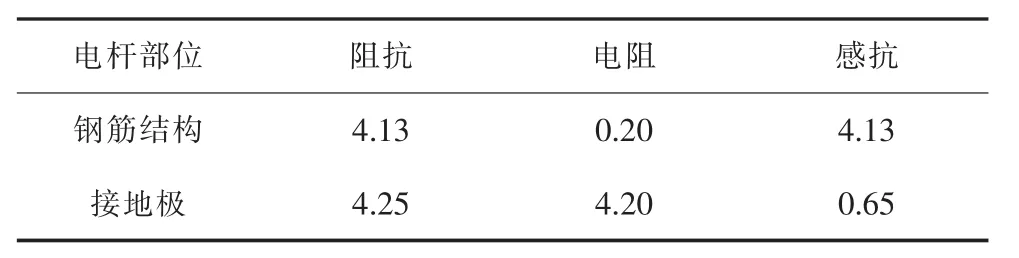
表4 8／22 μs雷电流下电杆各部分阻抗值 Ω

由于钢筋结构电阻很小可以忽略不计，在2.6／50 μs、8／22 μs两种雷电流作用下，将电杆钢筋结构视为集总电感模型，则由它引起的塔顶电位

对2.6／50 μs，8／22 μs两种雷电流波形进行微分分析，结果如图5所示。两种雷电流波形di／dt最大值分别为1.94×109和 3.45×108，其比值为5.62，而仿真计算感抗值之比为5.47，基本相同。因此可以说明，钢筋结构感抗与雷电流波形上升速率密切相关，雷电流波头越陡，钢筋结构感抗越大。

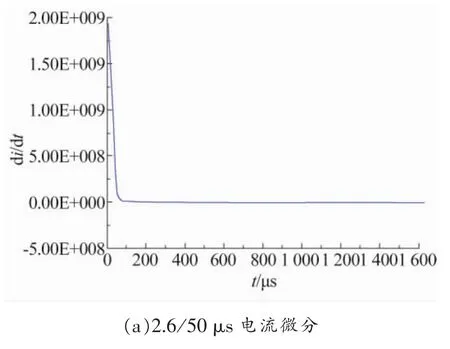
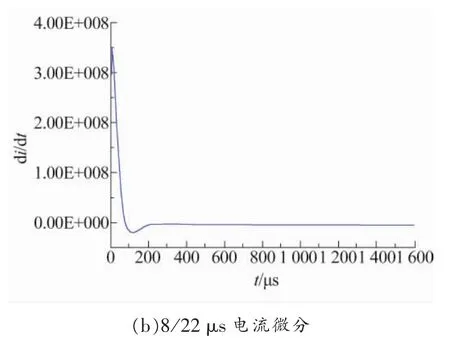
图5 雷电流波形微分分析

3 结语

电杆冲击接地电阻是输电线路防雷保护设计的重要依据，但是如果忽略了钢筋结构对塔顶电位的影响，而只是考虑接地电阻部分，将难以反映真实的塔顶电位，不利于防雷保护。通过常用输电电杆的CDEGS仿真证明，雷电流作用下，电杆钢筋结构会对电杆塔顶电位造成较大影响。而且相对于接地电阻而言，钢筋结构的阻值随雷电流波形变化更为显著。通过计算证明，电杆钢筋结构的阻值主要取决于随雷电流波形陡度，雷电流波头时间越短，钢筋结构感抗越大，对塔顶电位影响也就越大。

［1］陈军，郭军，王发义.Φ300预应力等径电杆导通电阻测量研究分析［J］.河南电力，2008（3）：46-49.

［2］徐华，吕金煌，文习山，等.杆塔冲击接地电阻的计算［J］.高电压技术，2006，32（3）：93-95.

［3］CHEN Y，ZHA X，ZHAO L.The measurement of impulse grounding resistance and inductance of grounding network［C］／International Conference on Energy Management and Power Delivery，1998.

［4］厉天威，何民，卢本初，等.输电线路杆塔接地电阻的简化计算［J］.电网技术，2011，35（9）：170-175.

［5］徐华，文习山，黄玲.关于冲击接地电阻测量的探讨［J］.高电压技术，2006，32（8）：79-81.

［6］李增，吴广宁，付龙海，等.双层结构土壤模型地网接地电阻的简化计算［J］.高电压技术，2008，34（1）：45-48.

［7］舒翔，文习山，张云建，等.杆塔冲击接地电阻测量仪的开发［J］.高电压技术，2004，30（10）：64-65.

［8］卢中山，张小青，李建修.一种有效的接地电阻测量方法［J］.电工电能新技术，2010，29（4）：44-47.

［9］王发义.110 kV输电线路电杆导通电阻测量研究分析［J］.华中电力，2011，24（3）：65-68.

［10］张艳梅.电气设备接地引下线导通测试及分析［J］.四川电力技术，2005，28（6）：8-9.

［11］GRECV L，RACHIDI F.On Tower Impedances forTransient Analysis［J］.IEEE Transactions on Power Delivery，2004，19（3）：1 238-1 244.

［12］李西敏，童创明，付树洪.介质体电磁散射的矩量法快速求解［J］.系统工程与电子技术，2008，30（3）：470-472.

［13］丁美新，李慧峰.雷电流波形的数学模型及频谱仿真［J］.高电压技术，2002，28（6）：8-10.

［14］刘平，吴广宁，隋彬，等.雷电流波形参数估计仿真研究［J］.中国电机工程学报，2009，29（34）：115-121.

［15］HEIDLER F，CVETIC J M，STANIC B V.Calculation of lightning current parameters［J］.IEEE Transactions on Power Delivery，1999，14（2）：399-404.

Influence of Reinforced Structure on Tower Top Potential

YUAN Weiqi，WEI Ning，SUN Zhenyong，SHI Leiyang，LIU Yongliang
（State Grid Qingdao Power Supply Company，Qingdao 266002，China）

When analyzing the lightning-shielding level of a transmission line，both the impulse grounding resistance and the reinforced structure of the tower should be considered.In order to analyze the influence of reinforced structure on tower top potential，CDEGS was used to build the simulation model of 10 kV distribution line tower and the potential of the tower top under versatile waveform lightning current was calculated.The result showed that the potential was different under versatile lightning waveform.The detailed calculation of reinforced structure and grounding resistance was drawn，and the result showed that the reinforced structure of tower had noticeable influence on tower top potential.Especially，when the wave head of the lightning current was steep，the inductance of reinforced structure increased significantly.In order to improve the lightningshielding level of a transmission line，the impulse grounding resistance should be reduced，and the reinforced structure should be improved，so that the inductance can be reduced.

CDEGS software；reinforced concrete tower；reinforced structure；lightning current；tower top potential

TM862

：A

：1007－9904（2017）04－0033－04

2016-11-20

苑维琦（1987），男，工程师，从事变电检修工作。