基于脉冲反射原理的HVDC系统接地极引线故障测距
2017-06-05任鹏飞谭博学姜晓东
任鹏飞,谭博学,刘 辉,姜晓东
(山东理工大学 电气与电子工程学院,山东 淄博 255049)
基于脉冲反射原理的HVDC系统接地极引线故障测距
任鹏飞,谭博学,刘 辉,姜晓东
(山东理工大学 电气与电子工程学院,山东 淄博 255049)
针对接地极引线的双极运行模式,利用脉冲反射法进行故障测距,分析脉冲信号在接地极引线上的传播特性,以及引线上可能出现的各种故障。以PSCAD为仿真平台,建立高压直流系统模型,模拟各种故障,并利用MATLAB进行数据处理与提取。对比分析不同故障类型下故障暂态行波与脉冲电压、电流反射行波信号,分别通过电压、电流波形求取故障距离,以求平均的方式得出最终测距结果。仿真结果表明脉冲反射法对接地极引线故障能够实现准确定位,此方法比故障暂态行波测距法应用范围广,波形辨识度高,测距精度高。
接地极引线;脉冲反射法;故障测距;PSCAD仿真
0 引言
高压直流接地极引线是整个直流输电系统中不可或缺的部分,实时监视与准确定位接地极引线上出现的故障可提高整个直流输电工程的安全稳定运行能力[1]。接地极引线长度通常是10~1 000 km,采用并行架空线路,具有分布参数特性。目前已有多种方法应用到接地极引线故障测距中,主要有电流差分法、阻抗法、行波法[2]。其中行波法不受线路参数分布不均匀、过渡电阻及故障类型等因素的影响,在实际工程中得到广泛应用,行波法分为A型单端行波测距方法、C型单端行波测距方法 (脉冲反射法)和D型双端行波测距方法。A型单端行波测距方法只需在线路的一端安装检测装置,简单方便,但波形分析困难,可靠性差;D型双端行波测距方法可靠性高,测距准确,但需在线路两端安装检测及通信装置进行相互配合;C型单端行波测距方法不需考虑故障暂态行波,在进行故障测距时可反复发射脉冲信号进行验证[3]。A型、D型行波测距法在文献[4-6]中已经得到学者的深入研究,不再赘述。在分析行波法故障测距的基础上,对脉冲反射法展开理论分析与仿真研究。
以PSCAD/EMTDC为仿真平台,建立高压直流输电系统模型,以脉冲反射原理为依据,分析接地极引线的双极运行模式,模拟线路故障,在线路始端发射单极性脉冲,利用MATLAB进行数据的处理与提取,由于脉冲电流与电压对故障的反应情况有所不同,因此分别分析并求取故障距离,最终通过求取平均值得出故障距离,以减小误差。由于接地极双极运行时接地极中有不平衡电流、电压,简单分析故障暂态行波并计算故障距离,仿真验证表明,脉冲反射法能够对接地极引线上易出现的故障进行准确的定位,测距准确,简单有效。
1 接地极引线运行特性
目前,世界上已投运的HVDC系统几乎都采用两端结构,只有一个换流站(送端)和一个逆变站(受端),两端换流站的中性点均连接接地极系统,即双极两端中性点接地方式(双极运行方式),如图1所示。

图1 双极两端直流输电系统示意
正常运行时,直流接地极系统双极运行方式又分为双极对称运行方式和双极不对称运行方式,双极对称运行方式是指两极的直流电压和直流电流均相等,此方式下两极的输送功率也相等,运行条件好,系统损耗小,可靠性高,是两极直流输电工程中最常用的也是最理想的运行方式;双极不对称运行方式是指两极运行电压或电流不相等,此时接地极中存在不平衡电流,即两极电流之差小于额定电流的1%。通常,当一极输电线路或换流站设备出现问题,需降低直流电压或电流运行时,才考虑双极不对称运行方式。双极对称运行方式下,由于换流变压器阻抗以及触发角等偏差,两极中的电流不是绝对相等的,接地极中有不平衡电流流过,线路中存在较小的电压[7-8]。
接地极系统在直流输电工程中具有重要的作用:一是其中一极需要停运检修时,接地极系统可利用大地 (或海水)作为回流电路过渡到单极运行方式,维持系统稳定的输送电力;二是接地极系统可钳制换流站中性点的电位,避免两极出现较大的对地不平衡电压,损害设备。
2 基于脉冲反射原理的接地极引线故障测距
2.1 脉冲反射法测距原理
脉冲反射法,又称C型单端行波测距法,其原理与A型单端行波测距法一样,如图2所示,不同之处在于,脉冲反射法不利用故障点产生的暂态行波,而是在故障后向接地极线路注入脉冲信号,脉冲信号在线路中传播遇到阻抗不匹配点会发生折反射,通过检测脉冲信号在发射点与故障点间往返的时间并根据脉冲的传播速度确定故障距离[9]。
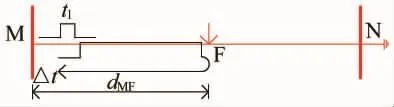
图2 脉冲反射法测距原理
由图2可知,在中性母线M端安装脉冲发射装置,N端为接地极端,假设在线路F处发生故障,dMF即为测量点到故障点的距离。
故障发生后在时刻tM1向线路注入宽度为t1的脉冲信号(正向行波信号),脉冲信号在线路中传播遇到故障点会发生反射,反射波表现为反向行波信号,在tM2时刻到达测量点,两者之间的时间延迟为Δt,故障测距步骤为:
1)根据脉冲电流反射行波得出的故障距离

2)根据脉冲电压反射行波得出的故障距离

3)最终结果
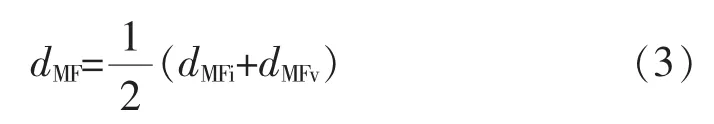
式中:v为脉冲行波在接地极引线上的传播速度。
若接地极引线未发生故障,则脉冲信号会一直传播到接地端发生反射,通过脉冲反射原理可以计算出接地极引线的全长,进而作为实际工程中对接地极引线长度的校验与矫正。
2.2 脉冲信号在直流接地极引线上的传播过程
脉冲信号在接地极引线上传播时,脉冲信号在故障点、中性母线和接地极端发生折反射,其行波折反射过程如图3所示。
由图3可知,M端注入的脉冲信号传播到故障点后,一部分信号发生反射向M端传播,另一部分发生折射向接地极N端传播,到达中性母线M端和接地极N端的信号都会继续发生下一次反射和折射,直到信号衰减完。因脉冲反射法属于单端行波测距,在确定故障距离时,只需要脉冲信号的发生时刻以及第一次反射脉冲到达测量端的时刻,所以图中省略了对脉冲信号在两端后续折、反射情况的描述。
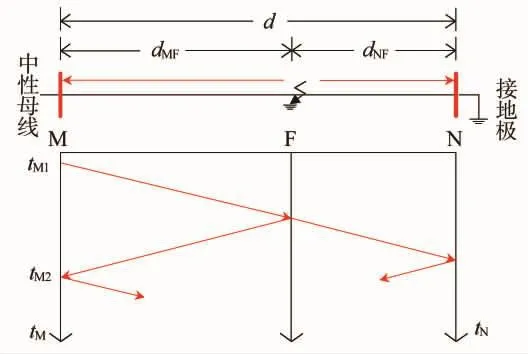
图3 脉冲信号传播过程
3 接地极引线故障及脉冲信号对故障的反映
接地极系统的运行情况直接影响直流输电系统的稳定安全运行,接地极引线所经地区多为树木丛生、地形复杂多变的山区,且线路较长,容易在遭受污秽、树枝放电或雷击后发生故障,接地极较易发生的故障有以下几种:断线故障,一般很少发生,通常是接地极线路倒塔或断路器跳闸使得线路开路;接地故障,又分为直接接地和经过渡电阻接地故障,工程实例表明,经过渡电阻接地发生较多,跨山区路段上的接地电阻不定,一般不超过300 Ω;雷击故障,是指线路在遭受雷击时,发生瞬间短路故障[10-11]。
向线路注入脉冲信号时,若线路未发生故障,线路阻抗处处相等,脉冲信号沿线路传播直到线路末端发生第一次反射,当线路存在故障,故障处的阻抗与线路特性阻抗不同,形成阻抗不匹配点,脉冲信号将在该点发生全反射或部分反射,成为线路上除末端外的另一个反射点。反射脉冲的极性和大小由反射系数P表示,表达式为
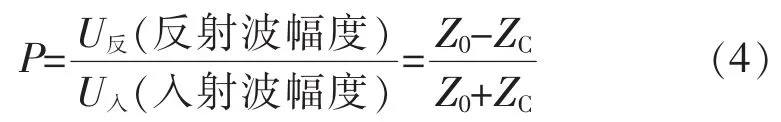
式中:Z0为传输线故障点的阻抗;ZC为传输线的特性阻抗。
当线路无故障时,ZC=Z0,P=0,线路上无反射脉冲;当线路发生断线故障时,Z0为无穷大,P=1,脉冲在故障点发生全反射,反射脉冲极性与入射脉冲极性相同;当线路发生直接接地时,Z0=0,P=-1,脉冲在故障点发生负的全反射,反射脉冲极性与入射脉冲极性相反;当线路发生经过渡电阻接地时,由于存在过渡电阻脉冲在故障点发生部分反射,反射脉冲极性与入射脉冲极性相反。不同故障时入射脉冲与反射脉冲如图4所示。
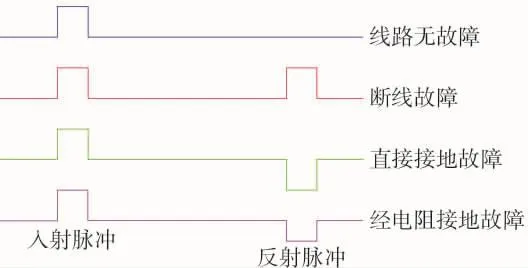
图4 不同故障的反射脉冲波形
由于矩形脉冲较易形成,具有陡峭的上升沿和下降沿,便于处理,仿真采用此脉冲波形。脉冲宽度越窄,其所包含的频率成分越高,波形易发生损耗甚至畸变,影响测试效果;宽度过宽则会使得发射脉冲与反射脉冲在近距离故障时相重叠,出现测试盲区[12],根据多次试验,取脉冲宽度t1=32 μs;脉冲幅值的选择应既不影响测试性能,又能使测试距离尽可能远,根据经验取幅值为48 V的脉冲信号。
4 仿真验证
4.1 仿真模型参数设置
为模拟直流接地极引线运行特性,利用电磁暂态仿真软件PSCAD建立双极平衡运行模式的高压直流接地极线路模型,如图5所示。
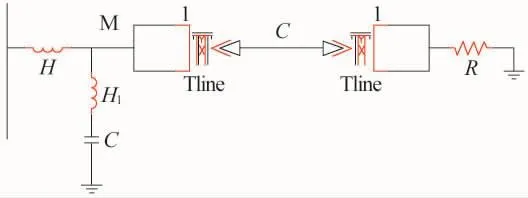
图5 高压直流接地极线路仿真参数模型
直流输电系统电压等级为500 kV,电流从换流变压器经中性母线流出,通过平波电抗器以及电容C和电感H组成的谐波滤波器,进入接地极引线,并分别流入两平行架空线路,在接地极线路末端经接地电阻R(电阻值为1 Ω)流入大地。接地极引线两平行架空线的长度都为100 km,在线路上设置故障点,在M处安装脉冲发射装置以及检测装置作为故障相和非故障相的测量点,系统仿真频率为1 MHz。
4.2 故障仿真
采用双极运行方式,设故障起始时间为0.6 s,故障持续时间为0.2 s,tM为第一个故障反射行波达到的时刻;在tM1=0.65 s注入幅值为正48 V的单极性脉冲,脉冲时长宽度t1=32 μs,tM2为第一个反射脉冲回到测量端的时间。根据文献[13]研究,行波在接地极线路中的传播速度v为298 000 km/s。图6~11中I1为故障线路电流波形,I2为非故障线路电流波形;V1为故障线路电压波形,V2为非故障线路电压波形。
4.2.1 断线故障
以30 km故障为例,将仿真图形用MATLAB进行数据处理与提取。
1)故障后,线路电流、电压波形如图6所示。图中,第一条红色虚线为故障发生时刻,第二条红色虚线为tM时刻。

图6 30 km断线故障波形
由图6(a)可知:tM=0.600 098 144 s,则 Δt=98.144 μs,dMFi=29.247 km。
由图6 (b)可知:tM=0.600 097 933 s,则 Δt=97.933 μs,dMFv=29.184 km。
最终结果:dMF=29.216 km, 测距误差约为0.784 5 km。
由图6可知,发生断线故障时,接地极引线故障线的电流减小,非故障线的电流增大;两线路的电压都增大,且出现波动,对换流站设备的稳定运行有一定影响。
2)故障后,施加脉冲信号后线路电流、电压波形如图7所示,图中第一条红色虚线为tM1时刻,第二条红色虚线为tM2时刻。
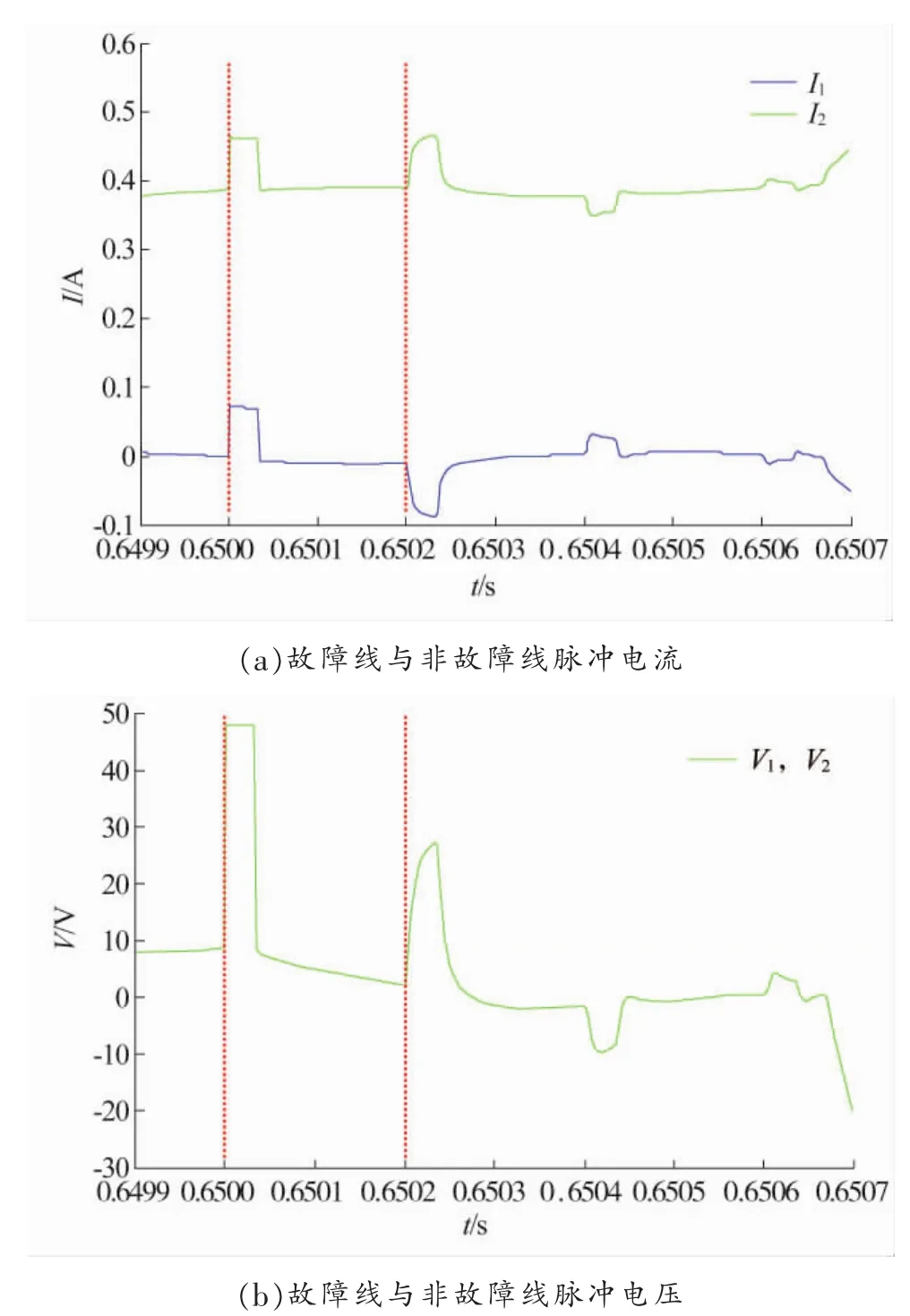
图7 30 km断线故障脉冲电流电压波形
由图7 (a)可知:tM2=0.650 199 054 s,则 Δt=199.054μs,dMFi=29.659 km。
由图7(b)可知:tM2=0.650 198 933,则 Δt=198.933 μs,dMFv=29.641 km。
最终结果:dMF=29.650 km,测距误差约为0.350 km。
由图7可知,故障线路和非故障线路脉冲电压相同,其反射波形与入射波形极性相同,但脉冲电压幅值受线路故障影响有所减小;脉冲电流在故障线路反射波形与入射波形相反,非故障线路的相同,因此在实际电路运行中通过波形极性判断故障类型并计算出故障距离。
设置不同的故障距离,分析电流、电压波形,分别用A型行波法和脉冲反射法计算故障距离,测距结果如表1所示。
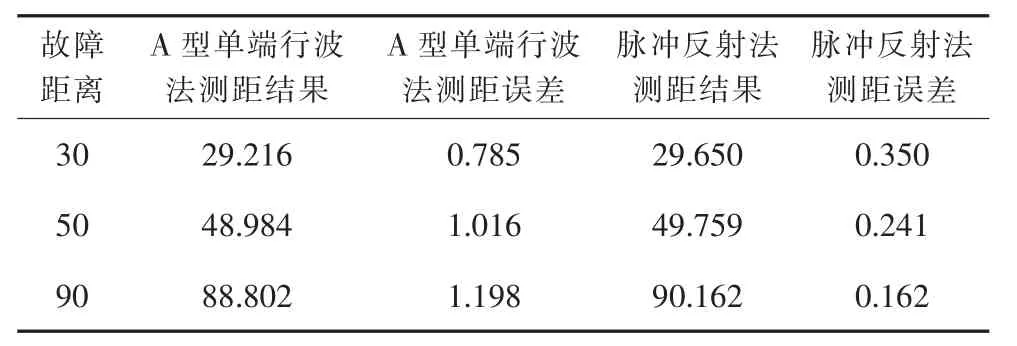
表1 断线故障仿真数据 km
多次仿真验证表明,线路断线故障时,A型行波测距法测距误差较大,不影响时域脉冲反射法对故障点距离的测定,脉冲波形反映准确,测距精度较高,满足故障测距的要求。
4.2.2 接地故障
由于接地极线路的接地电阻为1~1 000 Ω,仿真设置不同的过渡电阻值,以30 km故障、过渡电阻为1 Ω和90 km故障、过渡电阻为200 Ω为例进行仿真,结果如图8~9所示。

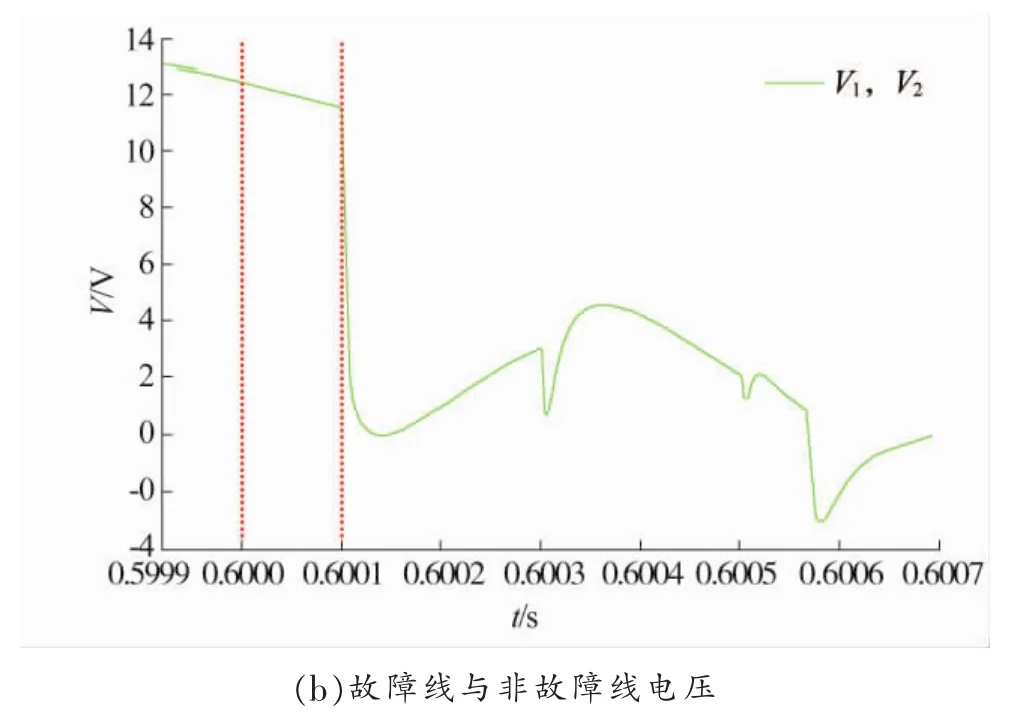
图8 30 km接地故障电流电压波形(过渡电阻1 Ω)
图8中第一条红色虚线为故障发生时刻,第二条红色虚线为tM时刻,由图8(a)可知:tM=0.600 099 443 s,则Δt=99.443 μs,dMFi=29.634 km。
由图8 (b) 可知:tM=0.600 099 443 s, 则 Δt=99.443 μs,dMFv=29.634 km。
最终结果:dMF=29.634 km,测距误差约为0.366 km。
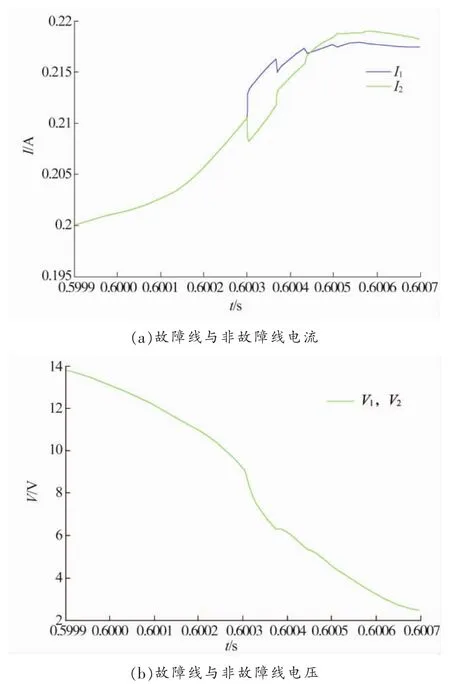
图9 90 km接地故障电流电压波形(过渡电阻200 Ω)
由图9可知,当过渡电阻为200 Ω时,故障电流电压波形不明显,无法计算故障距离。
由图8~9得出,直流接地极引线发生接地故障时,故障线电流增大,非故障线电流减小,故障线和非故障线电压变化相同,都减小。同时从两种故障状态的暂态波形可以看出,随着故障点过渡电阻及故障距离的加大,故障暂态行波的幅值减小,甚至不明显。

图10 30 km接地故障脉冲电流电压波形(过渡电阻1 Ω)
故障后,施加脉冲信号后线路电流、电压波形如图10~11所示。图中第一条红色虚线为tM1时刻,第二条红色虚线为tM2时刻。
由图10(a)可知:tM2=0.650 198 886 s,则Δt=198.886 μs,dMFi=29.634 km。
由图10(b)可知:tM2=0.650 198 933 s,则Δt=198.933 μs,dMFv=29.641 km。
最终结果:dMF=29.637 km, 测距误差约为0.363 km。
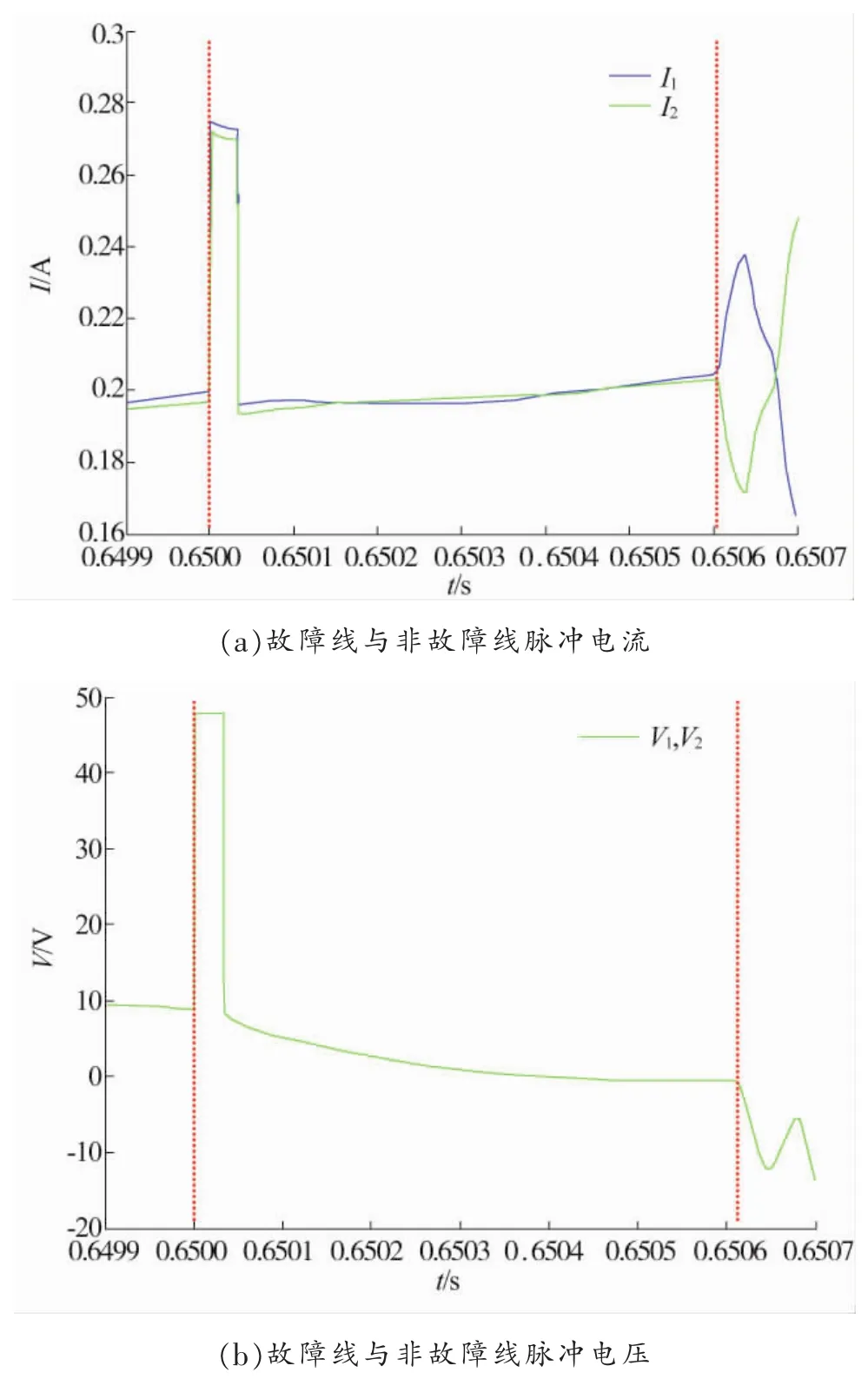
图11 90km接地故障脉冲电流电压波形(过渡电阻为200Ω)
由图11(a)可知:tM2=0.650 600 805 s,则Δt=600.805 μs,dMFi=89.520 km。
由图11(b)可知:tM2=0.650 605 812 s,则Δt=605.812 μs,dMFv=90.266 km。
最终结果:dMF=89.893 km, 测距误差约为0.107 km。
由图10~11可知,故障线路和非故障线路脉冲电压变化相同,其反射波形与入射波形极性相反,但幅值受线路故障影响有所减小;脉冲电流在故障线路反射波形与入射波形相同,非故障线路的相反,因此在实际工程中通过波形极性判断故障类型并计算出故障距离。
设置不同的故障距离,分析电流、电压波形,经A型行波法和脉冲反射法计算故障距离,测距结果如表2所示。

表2 故障仿真数据 km
多次仿真验证表明,接地故障过渡电阻较小时,A型行波测距法和脉冲反射法均能准确的实现故障测距,但随着过渡电阻增大以及故障距离加长,故障行波变得不明显,A型行波测距法测距难度加大且精度减小。虽然脉冲反射信号也会随着过渡电阻的增大及故障距离加长而反射幅度减小,但并不影响对反射脉冲信号的识别判断,并且可以通过加大脉冲信号的幅值克服这一问题,不影响故障测距。
5 结语
在分析高压直流输电工程接地极系统运行特性的基础上,论述了脉冲反射法的工作原理,分析了脉冲信号在接地极引线上的传播过程,接地极引线上易出现的故障及脉冲信号对不同故障行波的反射情况,利用PSCAD为仿真平台对各种故障进行仿真,并用MATLAB进行数据处理与提取,对电流、电压行波分别分析计算,仿真结果表明,脉冲反射法的应用范围高于A型行波测距法,能够判断接地极引线的故障类型,准确地实现故障测距,能够维持直流输电系统的安全稳定运行。
在利用脉冲反射法进行故障测距时,因线路损耗及故障,反射脉冲波形易发生畸变,不利于反射波起始点的正确识别,可研究准确识别反射波起始点的方法进而提高测距精度;还可以在脉冲信号选择、各种测距方法组合应用上做进一步研究。
[1]陈平.输电线路现代行波故障测距及其应用研究[D].西安:西安交通大学,2003.
[2]钟小垒.基于行波原理的直流输电系统接地级引线故障测距[D].淄博:山东理工大学,2012.
[3]王彩芝.直流接地极线路单端行波故障测距研究[D].淄博:山东理工大学,2014.
[4]王奎鑫,祝成,孙佳佳,等.输电线路组合行波测距方法研究[J].电力系统保护与控制,2012,40(15):82-86.
[5]郝洪民,陈平,梁凤强,等.直流接地极线路组合行波故障测距方法[J].国网技术学院学报,2015,18(4):6-10.
[6]蔡永梁,张楠,冯鸫,等.基于行波原理直流输电系统接地极线路故障测距系统设计[J].南方电网技术,2011,5(2):48-50.
[7]钟小垒,李京.基于行波耦合原理的高压直流输电系统接地极引线故障测距[J].山东理工大学学报(自然科学版),2012,26(3):54-59.
[8]钟小垒,李京.基于行波原理的双极直流输电接地极引线故障测距[J].山东电力高等专科学校学报,2012,15(4):5-10.
[9]王彩芝,姜映辉,王俊江,等.基于PSCAD/EMTDC的HVDC接地极线路故障仿真[J].中国电力,2014,47(2):69-72.
[10]李峰,徐丙垠.电弧反射电缆故障测距装置脉冲发射时刻选择算法[J].电力系统自动化,2011,35(13):88-91.
[11]张怿宁,束洪春,田鑫萃,等.特高压直流输电线路接地极线路高阻故障测距方法研究[J].电力系统保护与控制,2015,43(24):1-7.
[12]迟震.脉冲反射法电缆综合故障定位研究[D].哈尔滨:哈尔滨理工大学,2013.
[13]黄雄,王志华,尹项根,等.高压输电线路行波测距的行波波速确定方法[J].电网技术,2004,28(19):34-37.
HVDC System Grounding Line Fault Location Based on the Pulse Reflection Principle
REN Pengfei,TAN Boxue,LIU Hui,JIANG Xiaodong
(School of Electrical and Electronic Engineering,Shandong University of Technology,Zibo 255049,China)
Aiming at the bipolar operation mode of the grounding wire,the pulse injection method for fault location is used. Propagation characteristics of the pulse signal and various faults that may occur on the grounding wire are analyzed.Based on PSCAD simulation platform,the high voltage DC system model is established to simulate all kinds of faults,and the data of simulation results are processed and extracted by MATLAB.Comparing among signals of the fault transient traveling wave,the impulse voltage and the current reflected traveling wave,the fault distance is obtained through the voltage and current wave,and the final result is got in an average way.Simulation results show that this method has wider range of application,higher waveform recognition degree and higher ranging accuracy compared to the transient traveling wave ranging method.
grounding wire;the pulse injection method;fault location;PSCAD simulation
TM755
A
1007-9904(2017)03-0019-07
2016-10-17
任鹏飞(1992),女,研究方向为电网故障监测与定位。
