基于Floyd算法的交巡警服务平台管辖范围设计

吕静毅　常赛赛　聂佳琦　宋国浩

摘要：Floyd算是最常用的求两点间最短路径的方法，应用在很多领域，送货员送货，邮递员送信都需要事先考虑路途长短问题，而很常见的解决办法即是采用Floyd算法来对路径进行设计。评价交巡警服务平台的效率最主要的指标就是到达事发现场的时间，而决定到达时间的最主要因素是，服务平台距事发现场的距离，该文采用两点间距离公式对交巡警服务平台的管辖范围进行初步设计，后采用Floyd算法对特殊路口进行了规划。

关键词：Floyd算法；两点间距离；交巡警服务平台

中图分类号：TP311

文献标识码：A

文章编号：1009-3044（2017）10-0202-02

有困难找警察是我们每个人都知晓的，也是为人人流传的。警察肩负着交通管理、刑事执法、治安管理、服务群众四大职能，为了更有效地贯彻实施这些职能，需要在市区的一些交通要道和重要部位设置交巡警服务平台，以更好的服务群众。当某个路口发生突发事件时，警察必须以最快的速度即最短的时间到达事发现场，但是由于资源有限，不能为各个路口设置交巡警服务平台，政府必须根据不同地区的具体情况来合理地设置交巡警服务平台。

现如今解决此问题的方法有很多，本文采用两点间距离以及Floyd最短路径算法，对某市现有的20个交巡警服务平台的管辖范围进行设计。

1.获取数据

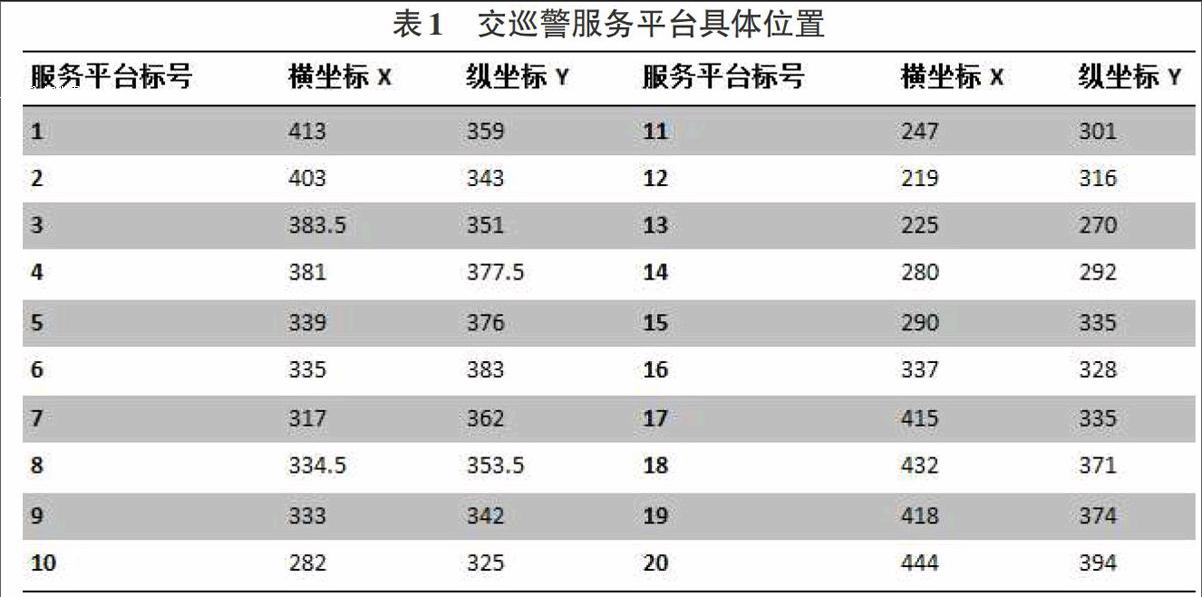
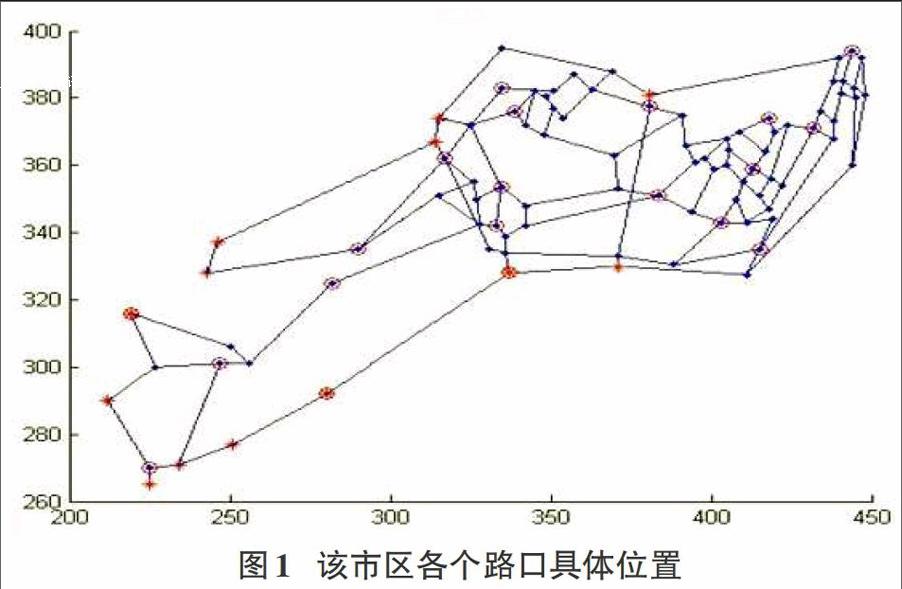
评价交巡警服务平台设计的是否合理，最主要的参考指标是警察到达案发现场的时间长短，若能保证每个路口都能在案发时及时得到帮助，便认为交巡警服务平台设计较为合理，想要很好的设计管辖范围必须知道各个交巡警服务平台的具体位置、市区各个路口的具体位置，本文搜集到某市区的20个现有交巡警服务平台如下表1所示，以及该市各个路口的具体位置如下图1所示，其中加圆圈的路口代表现有的交巡警服务平台的位置。

3.距离公式求解

该市警车的平均速度为60Km/h，要求警车能在3分钟内到达事发现场，由此我们可以知道交巡警管辖的路口应在3Km内。

利用上述两点间距离公式求解交巡警服务平台与各个路口之间的距离，采用MATLAB画图工具以每个交巡警服务平台为圆心，以3Km为半径做圆如图2所示。

上图中，以交巡警服务平台为圆心3Km范围内的路口均归该平台管辖，且设有交巡警服务平台的路口归该服务平台管理，这样就能够保证警察在规定时间内到达案发现场，能够及时处理突发事件。

4.Floyd算法处理特殊路口

由以上初步分配我们可以将一部分路口分配给距离最近的交巡警服务平台，但是由上图我们可以看出有些路口距每个交巡警服务平台的距离均大于3Km，有些路口距多个交巡警服务平台均小于3Km，此时仅仅用两点间距离公式计算已不能满足，因此本文采用Noyd算法计算最短路径，来确定特殊路口的管辖方法。

采用MATLAB直接將数据导人，得出各个交巡警服务平台的管辖范围如下表2所示。其中加口的路口标号表示距多个交巡警服务平台的距离均小于3Km，加（ ）的路口标号表示距每个交巡警服务平台均大于3Km的路口。

5.结束语

由以上的分配结果我们可以看到一些交巡警服务平台仅仅管理本身所在的路口，而有些交巡警服务平台却需要管理多个路口，这将会造成个别服务平台工作任务少，而一些服务平台却有繁忙的工作任务，工作任务的不均衡分配可能会导致工作效率下降。因此本文建议该市区在路口较多的地方适当增加服务平台，例如在1号，20号交巡警服务平台附近重新设置服务平台，从而减少1号，20号服务平台的工作量，提高工作效率。