基于多相流数值模拟的环卫车集污罐结构优化
2017-06-05邓刚林余晨光黄洪飙
李 卓 邓刚林 余晨光 黄洪飙 柳 超
(武汉理工大学现代汽车零部件技术湖北省重点实验室1) 武汉 430070) (汽车零部件技术湖北省协同创新中心2) 武汉 430070)
基于多相流数值模拟的环卫车集污罐结构优化
李 卓1,2)邓刚林1,2)余晨光1,2)黄洪飙1,2)柳 超1,2)
(武汉理工大学现代汽车零部件技术湖北省重点实验室1)武汉 430070) (汽车零部件技术湖北省协同创新中心2)武汉 430070)
罐式环卫车罐体结构及流场特性是决定车辆作业性能的关键,某罐式环卫车气力输送系统壁面区域不合理结构无法提供有效扰流增加稀疏悬浮多相流能量耗散,导致不合理的内流场难以改善尘粒平衡特性实现重力沉降.借助CATIA与ANSYS-FLUENT工作平台建立集成气路管道和集污罐系统于一体的CFD仿真模型,分析不同结构形式降尘挡板对气路系统集污罐内流场分布的影响;为了分析罐体内颗粒运动轨迹及集污效果,基于DPM离散相模型进行了多相流分析,实现同时对气体及尘粒两相流体轨迹追踪.另外,引入逃逸率这一新指标定量评价集尘罐系统沉降特性.结果表明,未优化前35.1%的逃逸率减少至2.7%,沉降性能提高了32.4%.
集尘系统;多相流;逃逸率;降尘挡板;参数优化
0 引 言
目前,国内外洗扫车均为复合厢式集污结构,为保证洗扫效率多通过提高高压离心风机风力等途径,而罐式结构能充分发挥结构特点,更适应流体运动.气路系统是洗扫车的核心系统,直接影响洗扫车工作性能及效率[1].气路系统的中段集尘沉降室设计是洗扫车设计的关键技术之一.借助计算流体力学,针对气路系统内流场状态提出改进和优化设计方案是洗扫车系统设计的新思路[2].袁凤东[3]对管道与尘粒以及气流速度进行了全面的理论研究,阐述了气流转速、尘粒速度,管道阻力与管道内部速度等关系相互之间的影响,以及自由扩散模式下粉尘轨迹与粉尘重力的关系等问题.欧阳智江等[4]对带有卷边的吸尘系统吸嘴口进行了流场分析,提出了在吸嘴口流场的均匀分布有利于减小阻力,提高尘粒进入吸嘴的效率,通过对粒子相的运动轨迹分析,对吸尘系统以及集尘系统进行优化设计.
1 流场仿真分析理论
1.1 计算流体力学控制方程
计算机数值分析中通过动量守恒方程,连续性方程和能量方程以3个偏微分方程来揭示质量、动量和能量3大守恒定律[5].整个气路系统内都属于低速流动可忽略热传导,不考虑能量方程.
1) 连续性方程 空气属于连续相,单位时间内流出单元体的流体静质量之和等于该时间单元体内由于密度变化而减少的质量,反映出的是质量守恒定律.
(1)
式中:ρ为流体的密度,kg/m3;t为空气单元在单元体内的时间,s,u,v,w分别为速度在x,y,z上的分量,m/s.
2) 动量方程 在计算流体力学中,任何的流体流动,都满足动量守恒定律,即满足动量方程.动量方程的本质是牛顿第二定律,动量随时间的变化值与作用在该单元上各力的和值.动力守恒方程在X,Y,Z三个分量上的表达如下:
(2)
(3)
(4)
式中:ρ为静压力,Pa;τxx,τxy和τxz为流体粘性力在X方向分量;τyx,τyy和τyz为流体粘性力在Y方向分量;τxz,τyz和τzz为流体粘性力在Z方向分量;Fx,Fy和Fz为流体单元所受外力在X,Y和Z方向的分量;u,v,w为速度矢量U在X,Y,Z方向上的分量;t为时间,s.
1.2 数值离散方法
数值离散方法是利用计算流体力学常用的有限体积法进行分析,通过对流体区域划分成许多小体积单元,将待求解的守恒微分方程在任一体积单元及时间单元内对空间与时间积分,再对待求解的函数及其导数对时间以及空间的变化作合理假设,最后对已选定的变化方式积分并整理成一组关于节点上未知量的离散方程.有限体积法偏重于从物理观点构造离散方程.其中,每一个方程都是表达有限体积上物理量守恒.
1.3 计算模型
FLUENT工作平台提供多了多种物流模型,实现各种复杂情况下的模拟计算,现所研究的问题选用湍流模型联系新未知量和平均速度梯度.目前工程应用中湍流的数值模拟主要分为3大类:直接数值模拟、大涡模拟、基于雷诺平均N-S方程组的模型.现运用基于雷诺平均N-S方程组的模型,从模式出发点的不同,所运用的是涡粘性封闭模式里的两方程模式.常用的两方程模式有:标准k-ε两方程、可实现型k-ε两方程、低Reynolds数k-ε模型以及k-ω两方程模式等.现采用数值模拟标准k-ε两方程,该方程被广泛应用于各种复杂湍流模型中,且计算较为准确[6].
2 集污罐内流场仿真
2.1 无压尘挡板的内流场
在多相流仿真分析中,为更加直观的评价罐体内部的沉降特性,引入一新的评价指标:逃逸率.逃逸率是指在单位时间内从风机入口逃逸出的总质量与垃圾进入气路系统总质量之比.
式中:η为逃逸率;M1为风机入口逃逸出的总质量;M2为垃圾进入气路系统总质量.
为了更直观的了解颗粒进入罐体及其沉降状态,对颗粒相的摄入采用单点粒子摄入.将粒子进入管道的入口进行如图1的划分方式.共有74个分布均匀的粒子摄入点模拟74个尘粒被吸入管道,进入沉降罐进行沉降.
图1 管口粒子摄入位置(单位:mm)
当颗粒随气流进入管道中,开始会沿着气流方向运动,在自身重力作用下以及在与罐体壁面摩擦碰撞下,最后沉降在罐体底部,仿真结果显示出,跟踪74个粒子,其中逃逸26个粒子,逃逸率为35.1%,沉降效果不佳.
2.2 设计压尘挡板后集污罐内流场分析
加装挡板后,气流被挡板前端斜角和两侧斜角引流到罐体底部,撞击罐体,能量耗散更快,罐体内部整体速度较之前整体降低.尤其是底部有明显改善,未加装挡板之前罐体底部气流速度较快,不利于尘粒在罐体内部沉降.加装挡板之后,罐体底部平均气流速度在6 m/s左右,且远远低于尘粒的起动速度[7-8],利于尘粒沉降.
2.3 加装压尘挡板后集污罐多相流仿真分析

图2 颗粒在模型中的运动轨迹图
图2为颗粒在模型中的运动轨迹图,由图2可知,利用DPM模型对加装挡板的罐体进行仿真分析,对颗粒相进行轨迹追踪,追踪粒子74颗,逃逸粒子为12颗,逃逸率为16.2%.相较于原模型有较大改善.粒子沉降的位置集中在罐体前侧,以及罐体后端两侧.这是由于尘粒由管道出来,撞击挡板之后,沿着挡板斜角方向运动,大量尘粒会冲向罐体末端,使得末端不易沉降.当尘粒沿着罐体后端壁面运动到前端时,会与新流入罐体内部的尘粒流撞击,一部分动能较大的尘粒会穿过尘粒流,耗损大量动能,最终沉淀到罐体前端,另一部分动能较小的尘粒会随着新的尘粒流运动,沿着罐体后端两侧绕行,最终沉淀.
加装挡板之后的罐体结构对尘粒在罐体内部沉降性有较大改善,罐体内部压力场分布更加均匀,利于气流待遇尘粒的运输.气流在罐体内部整体速度降幅较大,尤其是罐体底部速度值降幅最大,使得速度分布更加合理.由DPM追踪尘粒运动轨迹可知,尘粒在罐体内部逃逸率也有相应的降幅.但是从速度场分布图和尘粒轨迹图都可以看出,挡板后端会出现局部涡流区域,且罐体底部速度虽然降幅较大,对底部沉降的尘粒还是会有扰动.所以对挡板的结构还有优化的空间.
3 挡板结构参数优化
挡板长度L=800 mm、宽度B=900 mm,前倾角α=45°、后倾角β=90°.定义宽长比iBL简化优化参数.在所研究模型中,宽长比iBL=1.125.
3.1 前倾角α对罐体内部流场影响
前倾角是挡板设计参数中十分重要的一个参数.图3显示了不同前倾角情况下罐体内流场分布情况.由图3可见,随角度减小,气流越靠近罐体末端,当角度减小到30°时,气流在撞击挡板前倾角后,沿着挡板上沿飞去,向罐体顶端撞击.若当角度继续减小,更多的气流会撞击到罐体顶端,失去挡板效果.
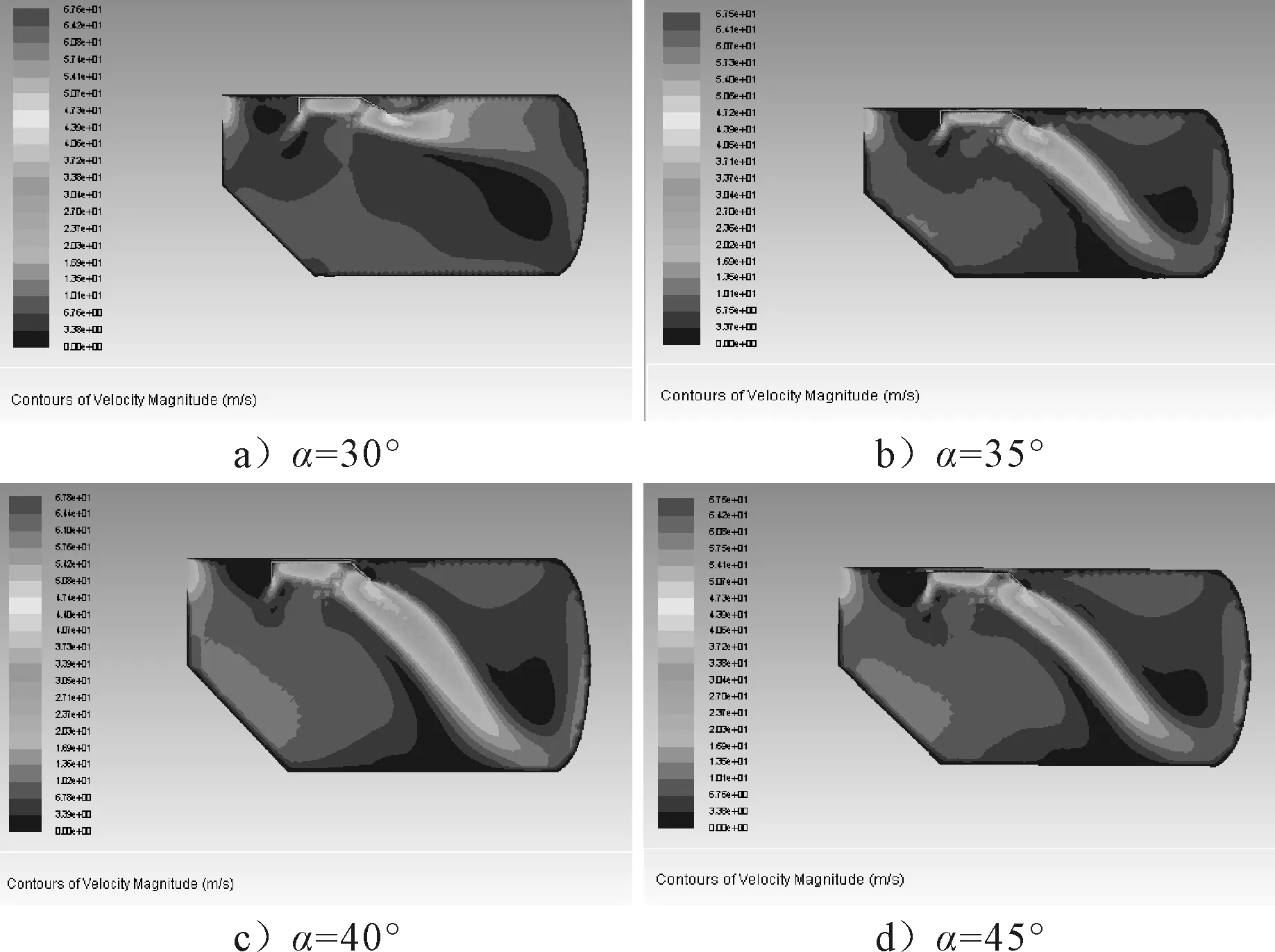
图3 前倾角对罐体内部流场影响图
为更直观的观察和评价挡板在不同前倾角下,罐体内部流场分布的合理性.图4显示了罐体底部从前端至后端气流随着位置变化曲面.从图中可知,在45°时罐体底部最大气流速度在8 m/s,40°时为9 m/s,35°时为4 m/s,30°时仅为1.2 m/s.从图中还知,前倾角在30°时,罐体底部气流速度波动最小,稳定在1 m/s左右,最有利于尘粒在罐体底部的沉降.
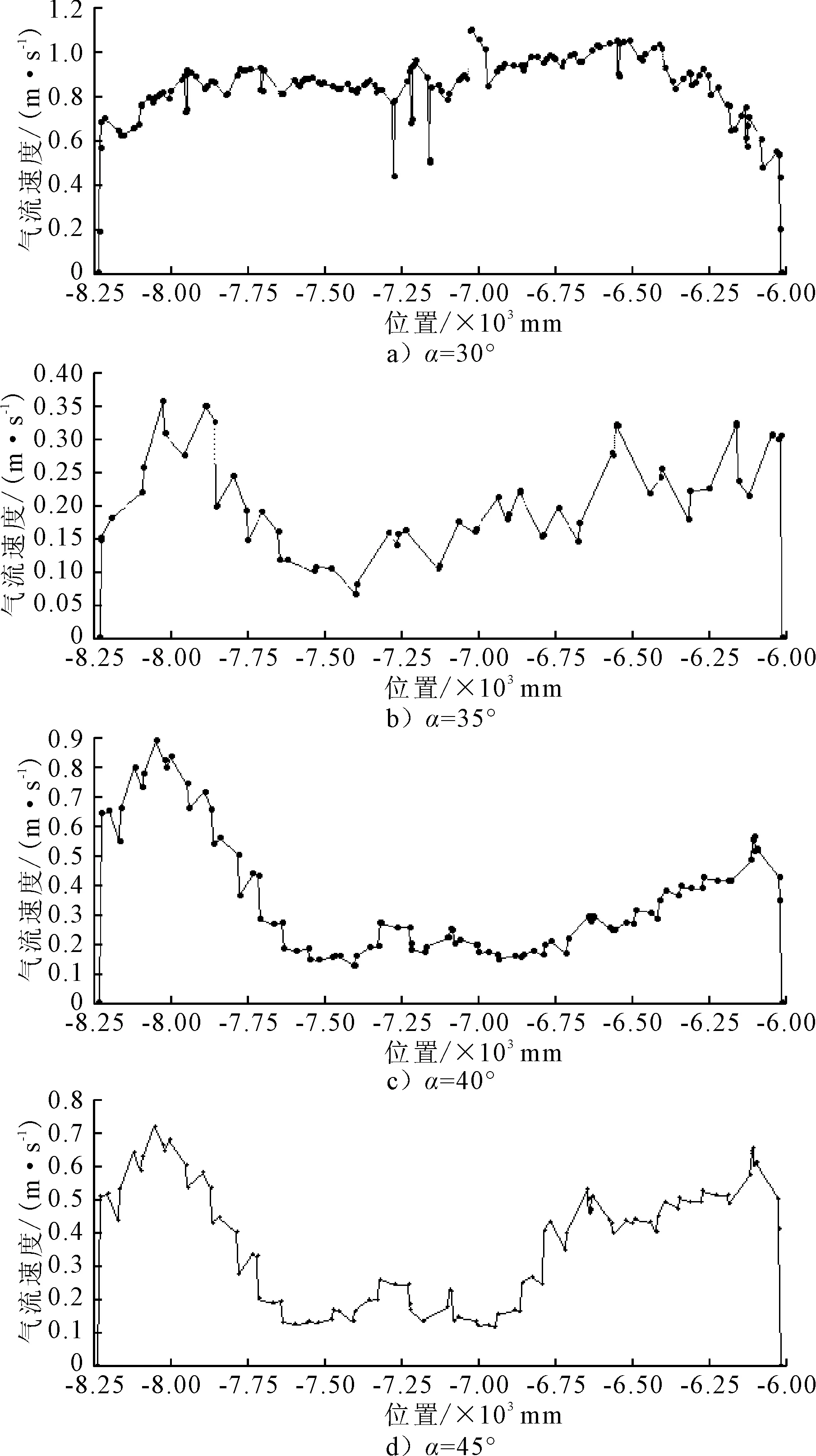
图4 不同前倾角罐体底部气流速度图
3.2 后倾角β对罐体内部流场影响
设定前倾角α=30°时,对不同后倾角β进行仿真分析.后倾角的取值范围为80°~100°.图5 为不同挡板后倾角其罐体内部速度流场分布,由图5可知,气流撞击挡板后,一部分气流会沿着挡板后方运动,沿后倾角方向.当挡板后倾角较大时,气流从后倾角流出后,其速度有向风机方向的分量,使得挡板后端与风机之间速度较大,不利于尘粒的沉降.然而当后倾角较小时,去气流速度主要向罐体内部运动,会带动尘粒向罐体底部运动,有利于尘粒在罐体内部的沉降.图6为不同后倾角挡板后端气流速度与位置关系图,由图6可知,当角度发生变化时,挡板后方气流速度也发生变化.当后倾角为100°时,挡板后端气流最大值为6.6 m/s;后倾角为95°时,挡板后端气流最大值为5.8 m/s;后倾角为85°时,挡板后端气流最大值5 m/s;后倾角为85°时,挡板后端气流最大值为4.3 m/s.显然,当后倾角小于90°时,气流速度小于或等于5 m/s,有利于尘粒的沉降.这是因为向挡板后方运动的气流在挡板后倾角压尘作用下,没有风机入口方向的分速度,所以挡板后端气流速度较小.当后倾角大于90°时,撞击挡板后倾角的气流会沿着角度方向运动,该速度产生了风机入口方向的分速度,所以其气流速度值会较高.经过比较分析得知,当挡板后倾角为80°时,气流最大速度为4.3 m/s,最小速度为3.3 m/s,更有利于尘粒在罐体中的沉降.
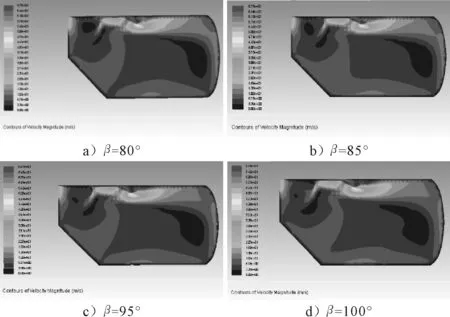
图5 不同挡板后倾角其罐体内部速度流场分布
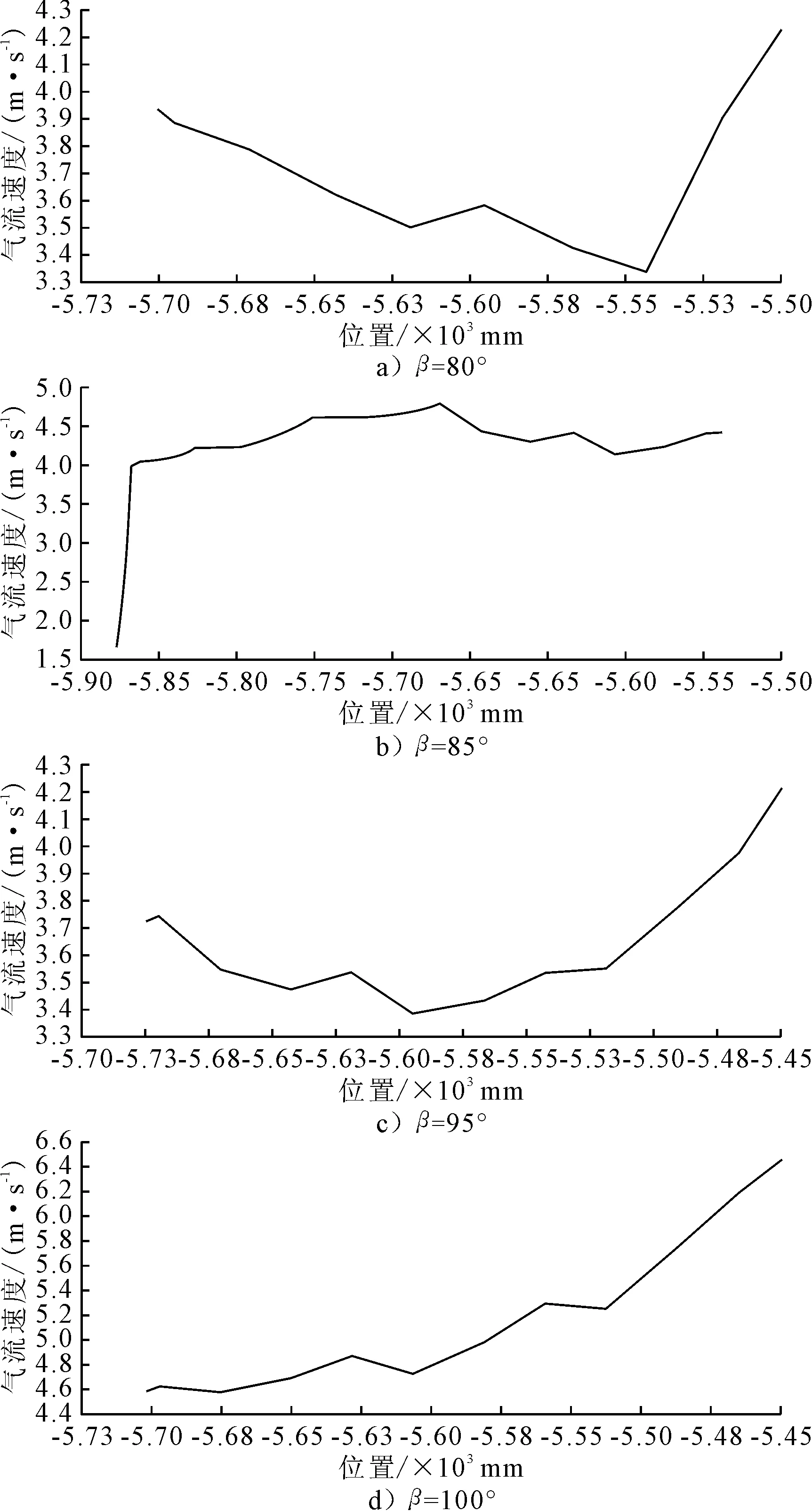
图6 不同后倾角挡板后端气流速度与位置关系图
3.3 宽长比对罐体内部流场影响
设定前倾角为30°,后倾角为80°,初步设定挡板宽度B=900 mm.原模型的宽长比iBL=1.125,通过改变挡板长度L,从而得出不同宽长比挡板对罐体内部流场影响.
图7为不同挡板长度其罐体内部速度场分布图.由图7可知,随着挡板长度的增大,从而宽长比减小,气流撞击挡板后会运动方向会逐渐向下.当挡板长度L=1 000 mm时,气流撞击挡板后会直接朝着罐体尾部运动,然后沿着壁面冲向罐体底部,大部分气流会从底部反弹沿罐体底部壁面运动,以及反弹的气流速度与尘粒沉降方向相反,会将悬浮或正沉降下来的尘粒上扬且对底部已沉降的尘粒造成冲击,对尘粒沉降不利.当挡板长度L=700 mm时,气流撞击挡板之后,会有大量的气流冲向罐体顶部,沿着壁面运动,也会导致罐体底部气流速度过快.为了让沉降有利,气流速度应该在罐体顶部速度较快,并由于撞击作用,使得能量耗散快.当气流到罐体底部时,气流速度应保持低速,使得尘粒在底部易于沉降且不受反方向气流速度的干扰.
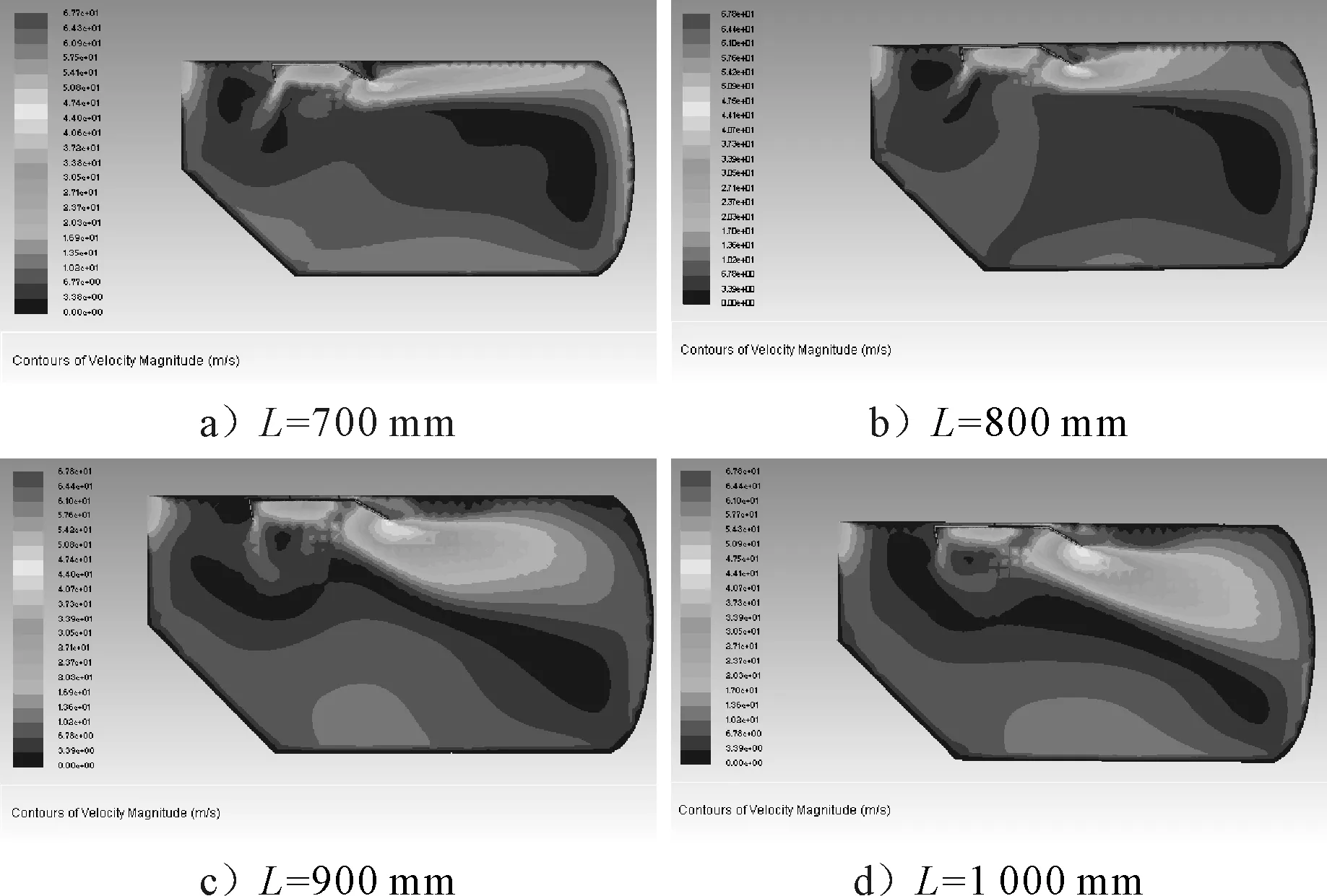
图7 不同挡板长度其罐体内部速度场分布图
图8为不同挡板长度其罐体中心线气流速度与位置,由图8可知,在挡板长度L=1 000 mm和L=700 mm时,罐体中心线上速度最高值为14 m/s,当L=800 mm时,最高速度为8 m/s;L=900 mm时,气流速度为9 m/s.综合判断,当L=800 mm,宽长比iBL=1.125时候,罐体内部流场分布最为合理,其中心线上最大值为8 m/s,整体平均气流速度在5 m/s以下,满足罐体内部沉降特性要求.
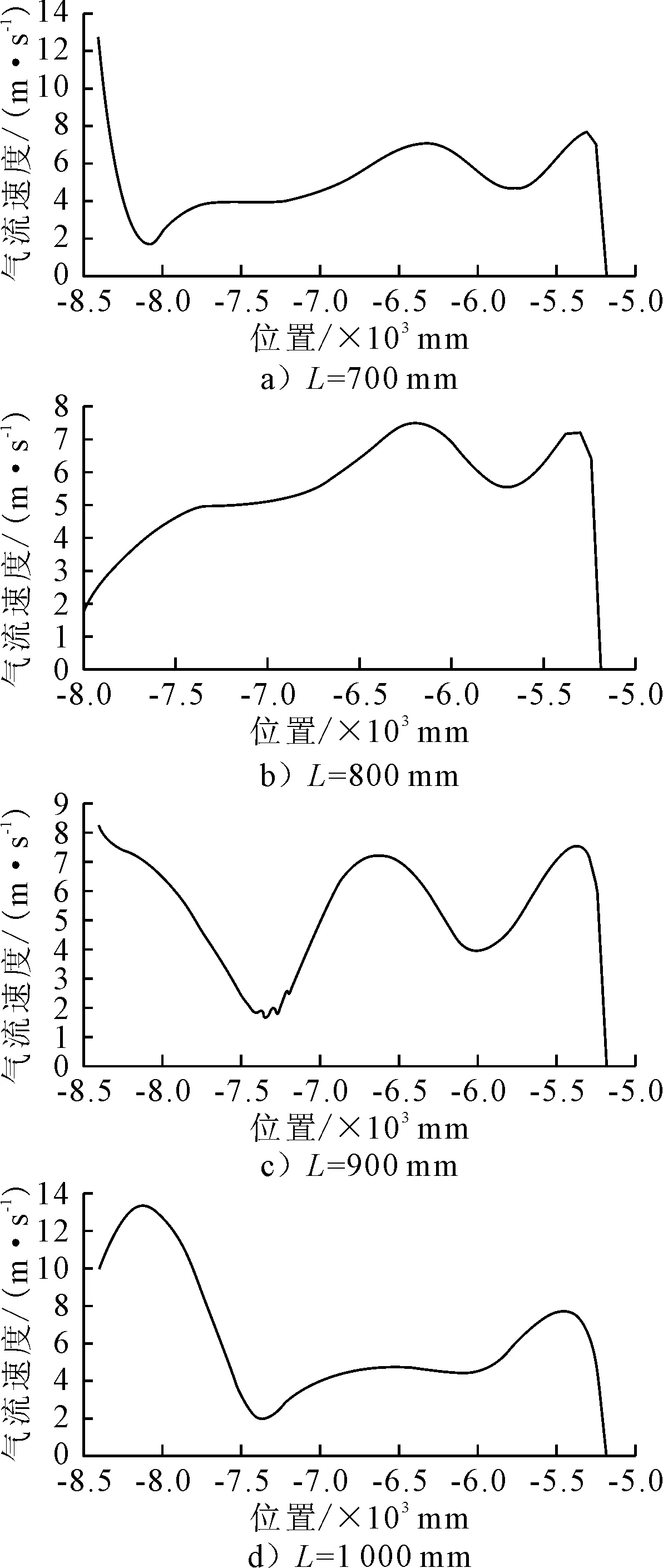
图8 不同挡板长度其罐体中心线气流速度与位置
3.4 优化后的罐体结构多相流分析
由于罐体结构外轮廓受到底盘空间及其附件的限制,不易改变.故对罐体内部加装一挡板且对挡板结构参数进行了优化设计.根据前文对罐体内挡板结构的优化,最终得到挡板参数如下:前倾角α=30°,后倾角β=80°,挡板宽长比iBL=1.125,其挡板长L=800 mm,宽B=900 mm.基于FLUENT平台,利用DPM离散相对在该模型下,尘粒的运动轨迹进行跟踪分析,得到结果见图9.
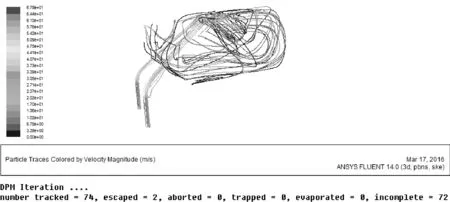
图9 优化后罐体结构尘粒运动轨迹图
由仿真结果可知,摄入74颗粒子,最后只有两颗粒子逃逸出罐体,其逃逸率为2.7%.相比之前未优化的16.2%有非常大的改善,达到了罐体沉降特性的要求.
4 结 论
1) 设计了一种全新的挡板安装在罐体内部,对气路系统及罐体进行了仿真模拟,得到了气路系统集污罐内流场分布.引入逃逸率这一指标来对沉降性进行评价,罐体内部流场相比原结构分布更加合理,逃逸率更小,更有利于尘粒在罐体中的沉降.
2) 针对压尘挡板结构对挡板的前倾角、后倾角、宽长比这3个设计参数进行了优化,通过对比分析得知,在前倾角为30°,后倾角为80°,宽长比为1.125时,挡板对罐体内部影响最为合理,可以让罐体内部流场分布合理,逃逸率优化到2.7%,达到较为理想的优化效果.
[1]王蓉.高速公路清扫车作业装置的研究[J].专用汽车,1995(4):20-26.
[2]PRASSLER E, ROHRMOSER B, SCHMIDL G. System design of a robotic road sweeper[C]. International Conference on Robotics & Automation, San Francisco,2000.
[3]袁凤东.水泥气力输送系统粉尘污染治理研究[D].天津:天津大学,2003.
[4]欧阳智江,章易程.卷边吸尘口流场特性分析[J].机械科学与技术,2013(3):362-366.
[5]VERTEEG H, MALALASEKERA W. An introduction to computational fluid dynamics[J].World Publishing Cooperation,2007(1):132-137.
[6]TU D. Computational fluid dynamics[J]. Butterworth Heinemann,2007(1):86-90.
[7]HILTON J, CLEARY P. The influence of particle shape on flow modes in pneumatic conveying[J]. Chemical Engineering Science,2011,63(3):231-240.
[8]朱伏龙,张冠哲,陈杰.真空吸尘车吸尘口的流扬仿真和结构优化[J].机械设计与制造,2008(11):576-582.
Structure Optimization of a Sanitation Vehicle’s Sewage Tank Based on Multiphase Flow Numerical Simulation
LI Zhuo1,2)DENG Ganglin1,2)YU Chenguang1,2)HUANG Hongbiao1,2)LIU Chao1,2)
(HubeiKeyLaboratoryofAdvancedTechnologyforAutomotiveComponents,Wuhan430070,China)1)(HubeiCollaborativeInnovationCenterforAutomotiveComponentsTechnology,Wuhan430070,China)2)
The tank structure and flow field characteristics are the key factors to determine the performance of the road sweeper. The unreasonable structure of the wall area of a tank type sanitation truck pneumatic conveying system cannot provide effective spoiler to increase the energy dissipation of the sparse suspended multiphase flow, resulting in unreasonable internal flow field that is difficult to improve the dust particle balance characteristic to realize gravity sedimentation. To solve this problem, CATIA and ANSYS-FLUENT are used to build the tank Gas pipeline and dust collector system, and the influences of different structure types of dust baffles on the flow field distribution in the tank of the gas system are analyzed. In order to analyze the particle trajectory and effect of pollutant accumulation in the tank, based on the CFD simulation model, DPM discrete phase model is used to analyze the two-phase flow trajectory of gas and dust particles. In addition, the new index of escape rate is introduced to quantitatively evaluate the settling characteristics of the dust collector system. The results show that the rate of escape is reduced to 2.7%, while the rate of escape before optimization is 35.1%. In addition, the settlement performance is improved by 32.4%.
dust collection system; multiphase flow; escape rate; dust baffle; parameter optimization
2016-12-28
U469.6
10.3963/j.issn.2095-3844.2017.02.012
李卓(1978—):男,博士,副教授,主要研究领域为汽车车身结构设计
