碳纤维增强重组竹受弯构件的极限承载力试验

周爱萍，刘睿，沈玉蓉，张苏鹏，于浩然，袁吉，李航

(1.南京林业大学土木工程学院；2.南京林业大学林业资源高效加工利用协同创新中心，南京210037)

碳纤维增强重组竹受弯构件的极限承载力试验

周爱萍1,2，刘睿1，沈玉蓉1,2，张苏鹏1，于浩然1，袁吉1，李航1

(1.南京林业大学土木工程学院；2.南京林业大学林业资源高效加工利用协同创新中心，南京210037)

重组竹是一种竹基高强复合材料，适用于装配式梁柱结构，但还难以满足现代大跨建筑结构的需求。在重组竹梁受拉区粘贴轻质高强的CFRP(carbon fiber reinforced polymer)，可充分发挥重组竹的受压性能，提高重组竹受弯构件的极限承载力。虽然重组竹的顺纹受拉应力-应变关系呈完全线性，但由于重组竹的顺纹受压应力-应变关系具有明显的非线性，故CFRP增强重组竹梁的极限承载力分析需要采用非线性模型。笔者通过CFRP增强重组竹梁采用简支梁4点弯曲试验，在研究其受弯破坏模式与破坏机理的基础上，导出了CFRP增强重组竹梁的极限承载力计算公式，并通过试验结果验证了公式的正确性。试验与计算结果表明，CFRP增强重组竹梁的破坏显示了明显的非线性特征，梁底分别粘贴一层、二层CFRP时，其极限承载力可分别提高14%和27%。

碳纤维增强聚合物(CFRP)；重组竹；力学性能；力学模型

重组竹是将竹篾(3 mm×15 mm×2 m)疏解成竹丝束，经蒸汽碳化干燥后浸胶，组坯热压(温度为110～160℃，压力为50～100 MPa)固化为型材[1-4]。重组竹在制造过程中消除了竹节、虫蛀、力学性能不均衡等缺陷，保留了在竹材中起着载荷增强作用的竹纤维。因此，具有均匀一致的力学性能。研究表明，重组竹材料是一种纤维增强各向异性的复合材料，顺纹与横纹的力学性能相差很大，而顺纹的抗压、抗拉力学性能差异也很大(顺纹的抗拉强度约为140 MPa，抗压强度约为60 MPa)[5-6]。其顺纹抗拉应力-应变关系呈完全线性关系，为脆性破坏；而其顺纹抗压应力-应变关系具有明显的非线性，为塑性破坏。且重组竹强度与刚度小于传统结构材料，故重组竹梁难以满足中、大跨结构的需要。采用质轻高强的碳纤维增强聚合物(carbon fiber reinforced polymer，CFRP)增强重组竹梁，可以充分利用重组竹的抗压性能，一定程度上提高受弯构件的极限承载力。在过去的20多年中，CFRP被广泛应用于木构件的增强与修复[7-10]。国内外学者对CFRP增强木构件的力学性能包括承载能力、刚度的计算模型及破坏模式等做了相关研究[11-15]。类似于木构件，若在重组竹受弯构件的抗拉区粘贴CFRP材料，增强其抗拉性能，即可充分利用重组竹的抗压性能的非线性，从而达到提高重组竹受弯构件极限承载力的目的。但目前使用重组竹作为建筑结构构件基本参照各国木结构规范进行设计，而现有规范计算模型均是基于线弹性理论，完全忽略了材料的非线性，因此低估了极限状态下的承载能力。

笔者通过4点受弯静载试验，研究CFRP增强重组竹受弯构件的破坏模式与力学性能，并建立其极限状态下承载力的非线性计算模型，该模型考虑了重组竹材料受压应力-应变关系的非线性，可以准确预估CFRP增强重组竹梁的极限承载力。

1 材料与方法

1.1 试验材料

基于欧拉梁理论的承载力计算方法仅涉及材料的顺纹力学性能，不涉及横纹力学性能。故本研究仅考虑重组竹的顺纹应力-应变关系。重组竹的顺纹应力-应变关系可表达为[5]：

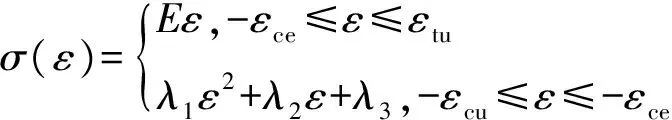
(1)

式中：E为弹性模量，MPa；λ1、λ2、λ3为材料参数，分别按下式计算：

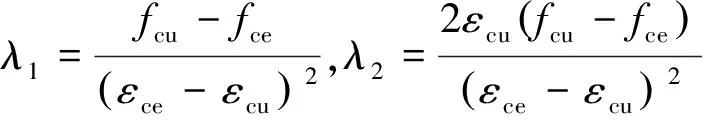
(2)

式中：ftu和εtu、fce和εce、fcu和εcu为重组竹顺纹本构关系中的重要参数，分别代表材料的极限抗拉强度和相应的应变、抗压比例极限和相应的应变、极限抗压强度和相应的应变。这些参数均可以根据单轴受拉、受压试验确定。CFRP作为重组竹受弯构件的增强材料，因其强度、弹模远高于重组竹，可认为它在试验过程中一直处于弹性阶段，应力-应变关系为：

(3)

式中：Er为CFRP的弹性模量；frtu和εrtu分别是其抗拉强度与相应的应变。参照ASTM D143-14标准和ASTM D3039/D3039M-14标准，测得A、B两组重组竹和CFRP的力学参数见表1。

表1 重组竹和CFRP顺纹力学参数Table 1 Mechanical parameters of PSB and CFRP in parallel-to-grain direction

试验所用重组竹受弯构件由江苏省森大竹业有限公司生产，构件有两种规格，分为A组和B组，构件长度均为1 880 mm，梁计算跨度为1 700 mm。试件截面尺寸与分组情况见表2。在重组竹受弯构件底部粘贴不同层数的CFRP布，研究CFRP层数对重组竹受弯构件的增强效果，同时采用不同的剪跨比，研究剪跨比对抗弯性能的影响。

1.2 试件制作

参照GB 50367—2013《混凝土结构加固设计规范》、《碳纤维片材加固混凝土结构技术规程》CECS 146-2003(2007版)的相关要求粘贴CFRP，粘贴环境温度为20℃，具体步骤如下：

表2 试件概况Table 2 Situation of the specimens

注：试件号首字母A/B表示不同的截面类型；A1/A2表示不同的剪跨比；R表示有CFRP增强。

1)CFRP布的配备：根据试验方案裁剪CFRP布，不得损伤其纵向纤维丝；

2)重组竹构件的界面处理：为保证两者的黏结强度，符合两者无滑移的基本假定，必须对粘贴界面进行处理。去除表面的尘土、油污等杂质后，粗砂纸打磨到光滑平整，最后用丙酮清洗表面并晾干；

3)粘贴CFRP布：按2∶1的比例进行配制环氧树脂AB胶，均匀涂抹在试件底面，厚度适中。胶凝结周期内，将CFRP布条平行拉紧迅速粘贴到位后，用涂胶刮板纵向多次均匀刮压，挤出气泡，保证黏结效果，并在CFRP布条的外表面再均匀涂抹一层环氧树脂胶；

图2 跨中荷载-位移曲线Fig. 2 The mid-span load-deflection curves

4)养护：在恒温20℃的室内养护10 d，待树脂完成固化后再进行试验。

1.3 试验方案

试验在南京林业大学土木结构实验中心进行，参照ASTM D198-02、GB/T 50329—2012《木结构试验方法标准》，采用简支梁四点弯曲静载试验(图1)。在受弯构件跨中位置侧面均匀粘贴5个应变片(3 mm×20 mm，灵敏系数为2.06)，以测跨中截面的应变；在跨中位置设有YHD-50型激光位移计，对跨中挠度进行测定。采用TDS-530静态数据采集仪同步采集荷载、位移、应变等数据，采集频率为1 Hz。试验通过杭州邦威30 t液压伺服仪采用位移控制方式进行加载，加载速度为2.5 mm/min，试件破坏控制在20 min内，以消除材料的蠕变影响。

图1 试验示意图Fig. 1 Schematic diagram of test set up

2 结果与分析

荷载-位移曲线与典型破坏模式见图2和图3，荷载-位移曲线具有明显的两个阶段：线性阶段和非线性强化阶段。加载到抗压比例极限之前，曲线呈完全线性关系；超过比例极限后，曲线由线性关系变为非线性，比例极限值约为极限值的1/3～1/2。因此，可以确定试件在最后阶段处于非线性状态。与之相应的试件状况是：加载到抗压比例极限之前，试件处于弹性阶段；超过比例极限后，构件受压区最外层应力超过抗压强度比例极限，进入塑性阶段，塑性区向内部扩展，而受拉区始终处于弹性阶段。试件原有的微孔等不断被压实、微裂纹不断扩展，因此，在加载到比例极限后开始不间断地发出轻微的声音。试件进入第二阶段后，由于纵向微小裂纹开始出现，刚度开始不断衰减，裂纹不断延伸、扩展，导致重组竹构件底部受拉区纤维断裂，断裂的竹纤维造成CFRP断裂，并不是达到其强度而破坏，试件破坏。构件跨中截面的应变情况见图4，可知中性轴不再保持在截面几何中心，不断移向受拉区，显示了顺纹抗拉强度与抗压强度之间的差异，同时验证了截面变形符合平截面假定。

图3 试件跨中典型的破坏模式Fig. 3 The typical failure mode of CFRP reinforced PSB at the mid-span section

图4 跨中截面应变分布Fig. 4 Strain distribution at the depth of the mid-span section

CFRP增强重组竹受弯构件单调加载破坏机理如下：当受压区最外层的应力达到抗压比例极限时，即进入非线性阶段，之前均处于线性阶段；随着荷载的增加，受压区的非线性区不断向内扩展，构件的损伤加剧；此时，试件截面的中和轴向受拉区移动；当构件受拉区最外层纤维达到抗拉强度极限值时，构件跨中底部纤维被拉断，最外层退出工作；继续加载，受拉区不断出现裂纹并向支座方向及中性轴方向扩展、延伸，不断有纤维被拉断，最后CFRP也随之断裂，构件破坏。试件极限承载力试验值结果见表3。由表3可知，重组竹受弯构件底部粘贴一层CFRP极限承载力比未增强梁提高约14%，二层CFRP极限承载力提高约27%，刚度变化不是很明显。试验采用不同的剪跨比以研究对受弯试验的影响，因剪跨比差异较小，构件未出现剪切破坏。

表3 试件极限承载力的试验值与理论计算值对比Table 3 Comparison of the ultimate load-bearing capacity between experimental and theoretical calculating results

3 极限承载力非线性力学模型

研究极限承载力非线性力学模型是基于欧拉梁理论与文献[16-17]等推导的公式，根据试件在试验中的破坏模式与机理，做了如下假定：1)截面变形符合平截面假定；2)两种材料黏结可靠，无滑移；3)极限状态时，CFRP的应变与重组竹构件的抗拉极限应变保持一致。

根据上述破坏机理的描述，试件的截面可以划分为3个区：受拉弹性区(ETZ)、受压弹性区(ECZ)和受压塑性区(PCZ)，参见图5。在PCZ区最外层的应力为极限抗压强度fcu，ECZ区与PCZ区边界应力为弹性抗压比例极限fce，ETZ区最外层的应力对竹纤维是σt=Eεt，而CFRP是σr=Erεt，E和Er分别为重组竹和CFRP的弹性模量，εt为ETZ区最外层的应变。

图5 试件截面应力-应变分布Fig. 5 The stress strain distributions at the bending member section

坐标y轴从截面中和轴指向受弯构件的受拉区，关于y的应力分布可以采用如下公式表达：

(4)

式中：k为受弯截面的曲率；f(y)为在PCZ区应力关于y的函数；yt、yce和ycp分别为ETZ、ECZ和PCZ区的高度。联合力平衡公式可得：

(5)

由积分公式(5)可得：

(6)

(7)

式中：b为截面宽度，mm；α为在PCZ区上应力分布不均匀系数，文献[16]已得到表达式：

(8)

从上式可知，系数α仅与材料的力学参数有关，这显然不正确，因为应力的不均匀性不仅与材料参数有关，还与塑性区扩展深度等有关。因上述推导中忽略了材料本构关系中的软化过程，而假定截面受压区、受拉区最外层应力达到强度极限值。虽然此估算会导致一些误差，但可以满足极限承载力的计算精度。

根据截面高度的几何关系与受弯截面的平截面假定，结合公式(6)、(7)、(8)可得：

(9a)

(9b)

(9c)

用ftu代替σt，根据上述极限状态截面每个区的高度，可得到试件的极限弯矩：

(10)

式中：ytu为极限状态ETZ的高度；Mu为截面的极限弯矩。将公式(4)代入上式得：

(11)

上式可以简化为3个部分:

Mu=Me+Mp+Mr

(12)

其中：

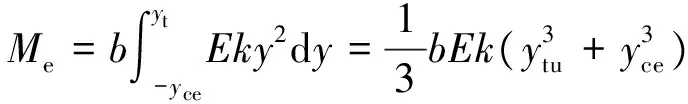
根据文献[16]有：

(13)

试件的曲率可以通过几何关系得到：

(14)

假定试件工作在弹性阶段，即ycp=0，联合力平衡关系、截面的几何关系与平截面假定关系可得到：

(15)

式中，R=ErAr/bE。

考虑σc=Ekyc，弹性阶段曲线可参见如下公式：

(16)

因此弹性弯矩计算公式为：

(17)

上述公式中将fce代替σc，即可得到达到比例极限值时的弯矩值。将计算值与试验值进行了对比(表3)，结果显示两者吻合良好，验证了上述极限承载力计算模型的可行性。

4 结 论

重组竹顺纹受压应力-应变关系具有很长的非线性阶段，而顺纹受拉始终保持线性关系，使得重组竹受弯构件具有明显的非线性。为充分利用抗压性能的非线性，在构件受拉区粘贴CFRP以增强PSB的受拉强度，达到提高受弯构件极限承载力的目的。粘贴一层、两层CFRP增强构件静载弯曲试验结果显示：粘贴一层CFRP能提高极限承载力14%左右；粘贴二层能提高极限承载力27%左右；但粘贴CFRP对刚度提高不明显。

本研究得到的极限状态CFRP增强重组竹受弯构件的极限承载力非线性力学计算模型，考虑了材料抗压性能的非线性，计算结果与试验结果吻合良好。

[1]周爱萍. 重组竹受弯构件试验研究与理论分析[D]. 南京:南京林业大学, 2014. ZHOU A P. Experimental study and theoretical analysis on PSB flexural member[D]. Nanjing:Nanjing Forestry University, 2014.

[2]汪孙国, 华毓坤. 重组竹制造工艺的研究[J]. 木材工业, 1991, 5(2):14-18. WANG S G, HUA Y K. A study on the manufacturing process of reconsolidated bamboo[J].China Wood Industry, 1991, 5(2):14-18.

[3]刘柏平, 程万里, 周建波, 等. 弧形原态重组竹制造工艺的初步研究[J]. 木材加工机械, 2009, 20(6):31-34. LIU B P, CHENG W L, ZHOU J B, et al. A preliminary study on manufacturing technology of bamboo engineering panel from laminated circular arc[J]. Wood Processing Machinery, 2009, 20(6):31-34.

[4]程亮, 王喜明, 余养伦. 浸胶工艺对绿竹重组竹材性能的影响[J]. 木材工业, 2009, 23(3):16-19. CHENG L, WANG X M, YU Y L. Effect of glue immersion parameters on performance of reconstitutedDendrocalamopsisoldhamilumber[J]. China Wood Industry, 2009, 23(3):16-19.

[5]HUANG D, BIAN Y, ZHOU A, et al. Experimental study on stress-strain relationships and failure mechanisms of parallel strand bamboo made from phyllostachys[J]. Construction and Building Materials, 2015, 77:130-138.

[6]ZHOU A P, HUANG D S, LI H T, et al. Hybrid approach to determine the mechanical parameters of fibers and matrixes of bamboo[J]. Construction and Building Materials, 2012, 35:191-196.

[7]KHALIL H P S A, BHAT I U H, JAWAID M, et al. Bamboo fibre reinforced biocomposites:a review[J]. Materials & Design, 2012, 42:353-368.

[8]BELPERIO R, GRAD I E. The performance of glulam beams reinforced with carbon fibre[J]. Proceedings of Pacific Timber Engineering, 1999, 2:99-106.

[9]LI Y F, XIE Y M, TSAI M J. Enhancement of the flexural performance of retrofitted wood beams using CFRP composite sheets[J]. Construction and Building Materials, 2009, 23(1):411-422.

[10]RAFTERY G M, KELLY F. Basalt FRP rods for reinforcement and repair of timber[J]. Composites Part B:Engineering, 2015, 70:9-19.

[11]谢启芳, 薛建阳, 赵鸿铁, 等. 碳纤维布加固木梁抗剪性能的试验研究[J]. 工业建筑, 2012, 42(6):88-91. XIE Q F, XUE J Y, ZHAO H T, et al. Experimental study on shear behavior of timber beam strengthened with CFRP sheet[J]. Industrial Construction, 2012, 42(6):88-91.

[12]AKBIYIK A, LAMANNA A J, HALE W M. Feasibility investigation of the shear repair of timber stringers with horizontal splits[J]. Construction and Building Materials, 2007, 21(5):991-1000.

[14]LOPEZ-ANIDO R, MICHAEL A P, SANDFORD T C. Experimental characterization of FRP composite-wood pile structural response by bending tests[J]. Marine Structures, 2003, 16(4):257-274.

[15]祝金标. 碳纤维布(CFRP)修复加固破损木梁的试验研究[D]. 杭州:浙江大学, 2005. ZHU J B. The experimental study of repairing and strengthening damaged wood beams with CFRP[D]. Hangzhou:Zhejiang University, 2005.

[16]HUANG D S, ZHOU A P, BIAN Y L. Experimental and analytical study on the nonlinear bending of parallel strand bamboo beams[J]. Construction and Building Materials, 2013, 44:585-592.

[17]HUANG D S, BIAN Y L, HUANG D M, et al. An ultimate-state-based-model for inelastic analysis of intermediate slenderness PSB columns under eccentrically compressive load[J]. Construction and Building Materials, 2015, 94:306-314.

Experiment study on ultimate load-bearing capacity of carbonfiber reinforced polymer reinforced parallel bamboo beam

ZHOU Aiping1,2, LIU Rui1, SHEN Yurong1,2, ZHANG Supeng1, YU Haoran1, YUAN Ji1, LI Hang1

(1. School of Civil Engineering, Nanjing Forestry University; 2. Jiangsu Co-Innovation Center forEfficient Processing and Utilization of Forest Products, Nanjing 210037, China)

Parallel strand bamboo (PSB) is a bamboo-based and fiber reinforced anisotropic composite which is increasingly used to fabricate beams and columns in building constructions. It is difficult for PSB to meet the needs of modern building structures with a large span. On the other hand, carbon fiber reinforced polymer (CFRP) is often used for enhancing and strengthening bamboo and wood structural member because of its lightweight. The CFRP pasted in convex side of PSB beams may fully utilize the compressive performances of this material and increase the load-carrying capacity of the member. The results of previous studies showed that the tensile constitutive law had linearity in parallel-to-grain direction, and the failure mode was brittle failure. However, its compressive constitutive law of PSB has obvious nonlinearity, and the failure mode is ductile failure. Therefore, the analysis on ultimate load-bearing capacity of CFRP reinforced PSB beams need to adopt the nonlinear model. The flexural performance of PSB beams reinforced with CFRP sheets was investigated in this study. Mechanical performances and failure mode of PSB bending members with and without CFRP reinforcement were studied by using 4-point bending experiments. Test results indicated that the damage of PSB beams presented pronounced nonlinear progressive process, and the load-carrying capacities of CFRP reinforced PSB beams could be obviously improved. However, the effect of enhancement on its stiffness was not obvious on account of not making the best of the strength of CFRP. An analytical model, taking into consideration the nonlinear constitutive relation of PSB composite, was developed to estimate the flexural performances of CFRP reinforced PSB beams. It was found that the load-bearing capacities of two-layer CFRP reinforced PSB beams averagely increased by about 27% when compared with the unreinforced members, and experimental results verified the validity of developed model.

carbon fiber reinforced polymer(CFRP); parallel strand bamboo(PSB)；mechanical properties; mechanical model

2016-11-14

2017-01-23

国家自然科学基金(51578291)；林业科学技术成果国家级推广项目([2015]21号)；江苏高校优势学科建设工程资助项目(PAPD)；江苏省大学生创新创业训练计划项目(201510298049Z)。

周爱萍，女，副教授，研究方向为现代竹/木结构。E-mail:zaping2007@163.com

TU531.3

A

2096-1359(2017)03-0137-06