使用博弈差分算法的电站锅炉高效低污染燃烧均衡优化

赵敏华，胡毅，李金，王羽笙，吴蕊，宋乐



使用博弈差分算法的电站锅炉高效低污染燃烧均衡优化

赵敏华1，胡毅1，李金2，王羽笙1，吴蕊1，宋乐1

（1西安建筑科技大学信息与控制工程学院，陕西西安 710055；2西安艾贝尔科技发展有限公司，陕西西安 710065）

提高电站锅炉热效率，降低NO等污染物的排放量是电站节能减排必须解决的问题。经过采用经量子遗传算法(QGA)优化参数后的最小二乘支持向量机(LSSVM-QGA)建立燃烧优化模型，预测的锅炉热效率和NO排放量的平均相对误差分别达到了0.054%和1.229%，其预测精度及泛化能力均较优，有更强的适用性能。在此模型基础上，提出一种采用自适应缩放因子与交叉因子和共享函数机制的差分进化算法(DE)，通过其演化博弈论中的NASH均衡，实现锅炉燃烧的多目标优化，结果表明，基于NASH均衡的优化方法可以得到操作变量的最优解集，能够更好地改善运行工况，最终可以实现削峰填谷，使电站锅炉保持一个稳定均衡的燃烧状态。

电站锅炉；优化；最小二乘支持向量机；模型；预测；差分进化算法；NASH均衡

引 言

我国能源结构以煤炭为主导，在推动经济腾飞的同时也严重污染了环境，而发电用煤是燃烧污染物的主要来源，大力推行高效清洁的火力发电技术是大势所趋[1]。电煤价格的不断上涨，发电企业成本压力与日俱增，同时为响应国家“节能减排”号召，对电站锅炉燃烧系统进行优化设计势在必行。

Haissig等[2-3]较早地将人工智能与电站锅炉燃烧优化控制相结合进行相关研究；王占能等[4]采用支持向量机对燃烧系统建模；许昌等[5]基于改进的最小资源分配网络算法建模，遗传算法多目标优化；方海泉等[6]使用贝叶斯神经网络对燃烧特性建模，遗传算法进行参数寻优；孙卫红等[7]采用最小二乘支持向量机对NO排放量进行预测；高芳等[8]采用最小二乘支持向量机建模的同时，使用粒子群算法实现对运行工况的寻优，达到提高炉效和降低NO排放量的目的。

传统的人工神经网络模型，具有参数设置较多，结果随机性强，训练时间长，易陷入局部最优及过学习等一些问题[9]；支持向量机(support vector machine，SVM)建模，在小样本问题建模中具有优势，其无局部极值问题，但当数据量增加，求解过程所需的计算资源变大，限制了其适用性；最小二乘支持向量机(least squares support vector machine, LSSVM)同样有SVM泛化能力强，全局最优的特点，其训练时间更短，更适合工程在线应用[10]。

传统的多目标优化，如文献[11]中的分析方法主要是对不同的优化目标进行权重分配，受主观因素影响较大，甚至需针对每一工况进行权值优化研究，这些都限制了该方法的实际应用。

差分进化算法(differential evolution algorithm, DE)采用实数编码，其一对一的竞争生存策略，基于差分的简单变易操作，基于种群的全局搜索策略，这些都降低了传统遗传操作的复杂性[12]；博弈论是一种研究主体之间冲突及相互合作的理论，主要研究相互作用的主体是如何做出选择和决策的[13]。将博弈论和智能优化算法结合，既具备优化算法的高效搜索性能，又包含博弈论多目标多标准的决策性，可以进一步提高原有优化方法的智能性。基于此，在参考前人的研究基础上，本文采用量子遗传算法(quantum genetic algorithm, QGA)优化LSSVM建立燃烧系统的非线性仿真的模型，继而使用改进的DE演化博弈论中NASH均衡的方法对锅炉热效率和NO排放量进行多目标优化。

1 基于最小二乘支持向量机的电站锅炉建模方法

1.1 最小二乘支持向量机算法

最小二乘支持向量机(LSSVM)是基于对传统支持向量机的改进，将不等式约束条件转换为等式约束[14]，而训练集的经验损失取为误差平方和的损失函数值，以此达到把二次规划问题变成线性方程组问题进行求解的目的，避免了二次回归问题的求解[15]，并且求解问题的速度和精度都有所提高。其运用于回归问题时的算法如下。

设有训练样本(x,y)，=1,2,…,，∈R（原空间），，则()在初始空间的表达式为

()=T()+(1)

其优化问题的描述为

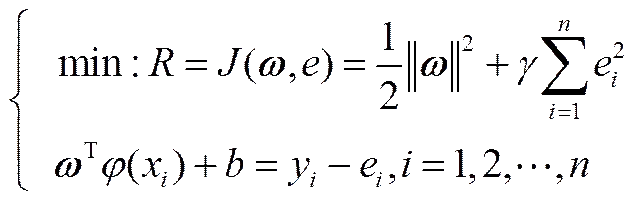
相应的Lagrange函数为

(3)

其中，∈R为权值向量；为偏移值（常数）；e为松弛变量；为正则化参数（正常数），其影响控制模型的泛化能力；=[1,2,…,]为Lagrange乘子；非线性函数()：R→R，其把数据映射到高维空间。根据优化条件

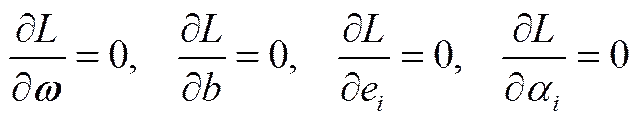
可得

(5)

由式(2)和式(5)，得线性方程

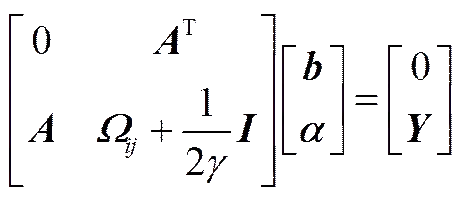
式中，=(x,x)，=(1,…,y)T，=(1,…,1)T，=(1,…,n)T，为单位矩阵。其中(x,x)为核函数，是()的内积，以式(6)完成初始空间的最小化问题的求解。

本文选用径向基核函数，其表达式为

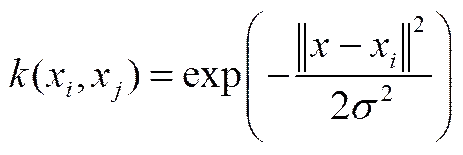
LSSVM最终的决策函数为

(8)

在利用其训练模型前，需确定核参数和正则化参数，两者值的选定直接影响所建立模型的性能[16]，其中反映了训练集的特性并影响模型的泛化能力，而对拟合偏差的校正和对模型的复杂度有很大影响，对此，已有诸多参数寻优方法的探索与研究[17-18]，其中应用较多的有网格搜索法与文献[19]中的交叉验证法等，这些方法对和进行机械搜索，但是降低了参数寻优的效率，本文采取的是QGA对参数寻优，以建立更准确有效的预测模型。

1.2 量子遗传算法

QGA是把量子计算、遗传算法结合起来的一种概率进化算法，其建立在量子的态矢量表示的基础之上。量子计算中进行信息存储单元的物理介质称为量子比特，将其概率幅表示应用于染色体的编码，使得一条染色体可以表达多个态的叠加，进而可以增加染色体的多样性，利用量子逻辑门实现染色体的更新操作，从而实现了目标的优化求解[20]，以达到更好的优化效果。

1.3 电站锅炉燃烧模型的建立

1.3.1 试验设计 试验研究平台为国内某电厂的500 MW机组配套的1650 t·h-1亚临界、低倍率再循环、一次中间再热、塔式布置全悬吊式锅炉，其燃烧方式为前后墙对冲。机组先后增加脱硫、脱硝系统以及更换低NO燃烧器后，锅炉的燃烧状况发生了很大的改变，后对该锅炉二次风优化燃烧进行了调整试验，以全面了解该锅炉的实际运行状况。

在300、400、450、500 MW 4组不同的机组负荷下，分别进行热态正交试验，并且分别对烟气含氧量，燃烬风挡板开度，一次风量，二次风配风等一些控制量进行变工况试验，具体试验方案可参考文献[21]，将得到的28组数据作为试验样本数据。部分建模试验数据如表1所示。

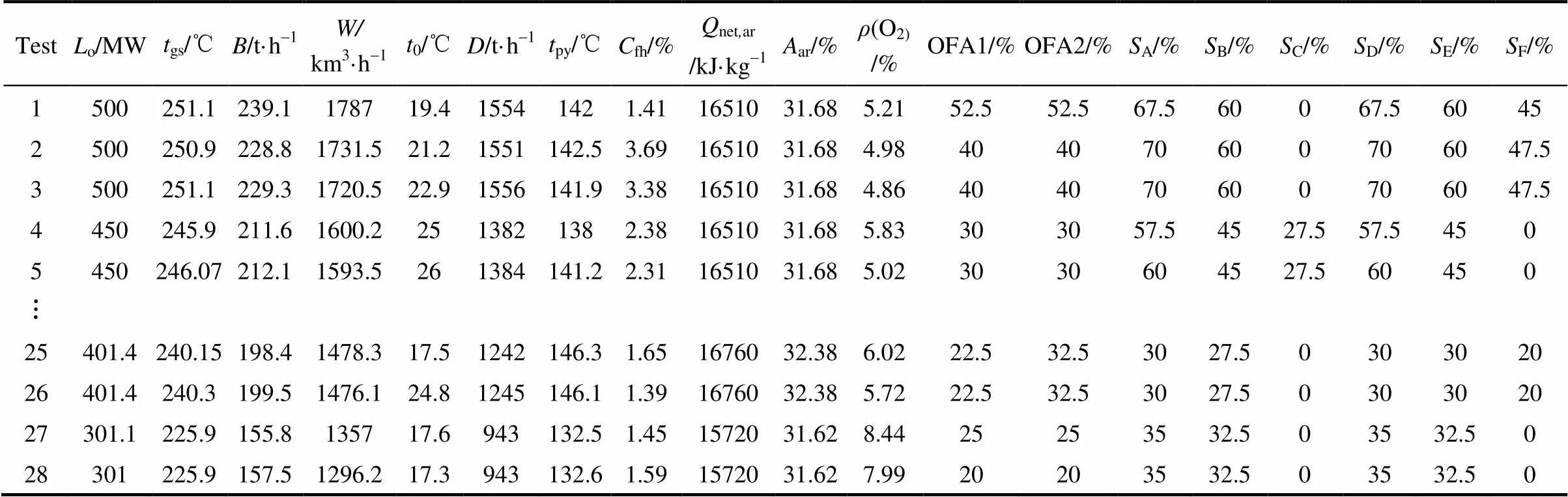
表1 热态试验数据

1.3.2 预测模型的建立 选取机组负荷（o）、给水温度（gs）和蒸发量（）表示锅炉负荷的影响，燃料量（）和送风量（）表示风煤比的影响，环境温度（0）表示周围环境温度的影响，排烟温度（py）和飞灰含碳量（fh）表示对热效率的影响，低位发热量（net,ar）表示煤质特性的影响，氧量（(O2)）表示燃烧氧量对NO排放特性的影响，前、后墙燃烬风风门挡板开度（OFA1、OFA2）表示燃烬风的影响，二次风风门挡板开度（ABCDEF）表示二次风配风对NO排放的影响，共19个参数作为输入变量，锅炉热效率（）和NO排放量（(NO)）为输出变量，建立燃烧特性的LSSVM预测模型。预测模型示意图如图1所示。

因为试验数据量级相差较大，输入和输出数据需经过预处理。

这里将数据归一化处理到[0.1，0.9]，归一化公式为

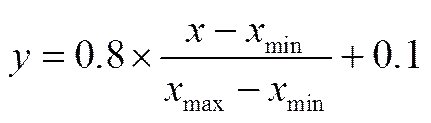
其中，、分别为归一化前后的数据值，max、min分别为样本数据归一化前的最大值和最小值，归一化处理可以使试验数据归一到统一量级，同时，预测模型的输出值需要经过反归一化处理，还原到原数量级，归一化和反归一化处理均通过MATLAB中的“mapminmax”函数实现。

本文中涉及的样本数据的建模与优化均经过归一化处理，包括后文博弈过程设置中受益函数涉及的变量均指归一化后的数值，建模和优化得到的最终结果经反归一化处理后再进行数据分析。

归一化之后考虑到建立模型维数较多，输入变量之间关联性较强，在此对样本数据进行主成分分析(principal components analysis, PCA)，其作用是将相关联的信息集中到几个综合指标，即主成分上，其是原始变量之间的线性组合，各主成分间为正交关系，针对复杂问题，PCA可以在不改变数据结构的情况下，简化样本，降低维数，提高效率，经过PCA，输入变量由19维降低为8维，可达到有效降低维数以提高预测模型的整体性能的目的，其具体实现可参考文献[22]。

实验环境为MATLAB R2010b，LSSVM采用的是LS-SVMlab工具箱，在LSSVM-QGA建模中，使用QGA确定核参数和正则化参数，寻优范围均设为（0.001～500），最大遗传100代，种群大小Size设为40，量子位数目为20。

采用留一法交叉验证的方法，应用所建动态模型对所有工况进行预测，即逐次将其中的27组数据用于训练，剩余1组数据用于测试，则共有28份数据，则可分别对所有28个工况样本进行预测，最后统计数据分析，这样可以进一步验证模型的拟合效果以及预测效果。

1.3.3 模型预测效果 所建立模型的预测效果如图2、图3所示。

图中的sample data指按运行参数通过国标公式[23]计算得到的热效率值。

由图2、图3可知LSSVM-QGA模型对锅炉热效率和NO值的预测效果及泛化能力均较好，预测值曲线与样本数据曲线拟合程度很高。

为对比效果，分别使用BP神经网络、SVM和LSSVM 3种模型对样本数据进行建模仿真。

采用留一法交叉验证的方法，其中，BP神经网络的结构为19-20-2，L-M训练算法，学习率为0.01，动量因子为0.9，迭代100次，训练目标10×10-5；SVM通过台湾大学林智仁的libsvm工具箱实现，其类型为epsilon-SVR，核函数为RBF函数，其他参数由PSO算法寻优得到，其中PSO的种群为20，代数为100，加速因子1，2分别为1.5和1.7，惩罚参数寻优区间为[0.1,100]，核函数参数寻优区间为[0.1,100]，损失函数值寻优区间为[0.01,10]；LSSVM模型的和通过QGA寻优得到，该模型的具体算法实现参考1.3.2节。

样本数据的仿真结果分别如表2所示，其中为平均绝对误差，为平均相对误差，RMSE为均方根误差。

由表2中数据对比可知，LSSVM模型比BP神经网络、SVM模型具有更高的预测精度，其预测结果的平均误差、平均相对误差及均方根误差均小于其他两种模型的预测值。

由表2可知，经所选模型预测的锅炉热效率和NO排放量的平均相对误差分别达到了0.054%和1.229%，其逼近和泛化能力足以满足电站锅炉燃烧特性的建模要求。

表2 LSSVM与BP和SVM的预测效果对比

2 基于博弈差分算法的燃烧优化

2.1 差分算法演化NASH均衡

DE的待定参数少，不易陷入局部最优，收敛速度快，是其最主要的优点，该算法已经成为一种求解非线性、不可微、多极值和高维度复杂函数的有效和鲁棒的方法[24]；由于其具有较好的鲁棒性和较强的全局收敛性能，且不需借助问题的特征信息，使其适于求解一些无法使用常规的数学规划方法解决的复杂环境中的优化问题[12]。

因NO在一定程度上与锅炉热效率是一对相互制约的变量，如何能在两者之间找到平衡点，既能实现提高锅炉热效率，又实现节能减排，实现多目标均衡优化，这个问题仍需大力研究以期找到更有效的解决手段。传统的权值分配法受严重的主观因素影响，适应性不广，且效果并不是最优，本文提出一种使用差分算法用以演化寻找多目标优化问题的NASH均衡解集。

博弈论又称对策论，是寻求多目标优化的博弈平衡的策略过程。在多目标多标准的优化决策性方面其具有很大优势，将会使结果更接近于实际过程。并缩短总体优化时间，改善收敛速度和提高计算效率，对于复杂问题，则可以实现模块化，并能提高求解质量[25]。

在博弈论的标准表述中，博弈主要包括决策者、策略集和受益函数三大要素[26]。

博弈的决策者∈，=(1,2，…，)；每个决策者的策略集为s，则所有决策者的策略集为={1，2，…，s}；当每个决策者的受益函数为f，则受益函数集合={1，2，…，f}。那么，可以用={，，}来表示博弈。

以锅炉热效率（决策者1）和NO排放值（决策者2）的双目标优化为例，其求取二者NASH均衡的数学表达公式为

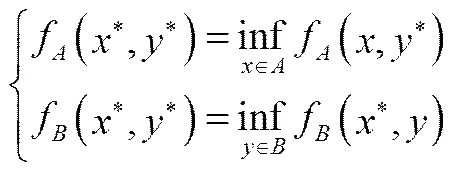
其中，、分别为和(NO)当前对应的数值，有∈、∈，与分别为二者对应的搜索空间，即策略集，f与f分别为二者对应的受益函数。则至少有一组策略（*，*）是二者的NASH均衡解。NASH均衡的模型结构示意图如图4所示。

图4 博弈策略模型结构

Fig. 4 Structure of game theory strategy model

由图4可见，每个决策者都拥有自己的优化标准，即受益函数，以及策略集。策略过程中，根据对方的策略不断调整自己的策略，使自己达到更优的策略标准，每代进化结束后进行信息即策略的交换[25]，当所有参与人都无法再改进自己的目标，系统即处于均衡状态，Nash[13]已证明，对任一有限策略型博弈，都至少将会存在一个混合策略NASH平衡。

本文以智能算法与博弈论相结合，使用差分算法演化NASH均衡，得到一种博弈差分算法，为改善优化效果，在原有差分算法基础上加入共享函数，通过引入小生境半径share，重新标定适应度函数[27]，参照Sigmoid函数制定自适应缩放因子，其表达式为

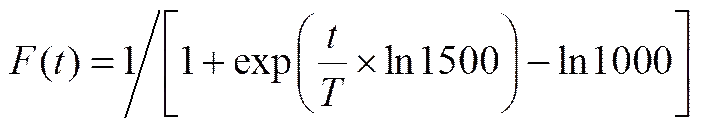
式中，为当前代数，为总的迭代次数。

交叉因子的表达式改为

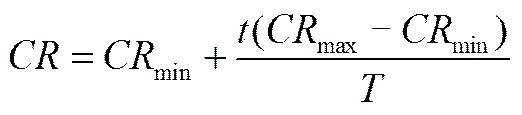
式中，min=0.3，max=0.9。

在此对Schwefel函数作为适应度函数进行测试，以验证所提出方法的有效性，该函数的数学表达式为

当=2时，其有最小值-837.9658。

仿真过程中，设种群规模为30，自适应和，share设定为420（经不断测试，此时算法寻优效果最好），算法迭代1000次，GA、PSO及DE为标准算法，未做改进，参数设置参考文献[24]，ADE为改进的DE算法，每种算法寻优30次并统计数据，以寻优值与最小值的平均绝对误差和均方根误差RMSE作为评价指标，仿真结果如表3所示。

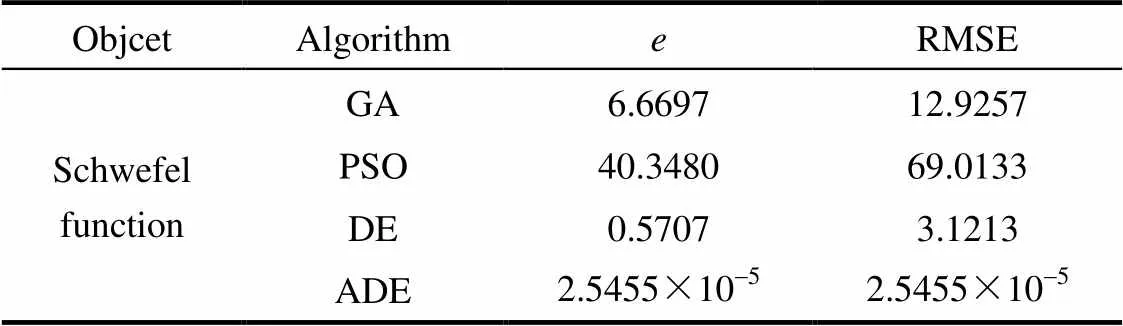
表3 仿真结果对比

由表3可知，在采用的几种方法中，改进的DE算法寻优30次的误差均为2.5455×10-5，寻优的准确度和稳定性均为最好，其中，各种算法的寻优过程曲线如图5、图6所示。

如图5可知，改进的DE算法克服了寻优初期过快收敛及易陷入局部最优的缺点，保持了种群的多样性，到寻优后期则寻优速度明显加快并找到最优解。

图6为图5中改进的DE算法对应的重新标定后的适应度曲线，由图可知，重新标定后，算法适应度寻优范围明显减小，并使得算法在寻优的初期保持较高的精度。

2.2 燃烧优化的实现

依据建立的模型，考虑到习惯运行方式及安全因素，在此设取氧量为1，调整范围为2%～5%，燃烬风风门挡板开度为2～3，调整范围为30%～60%和二次风风门挡板开度为4～9，调整范围为30%～70%，将其作为待优化的操作变量。

博弈过程设置为

决策者：炉效，NO排放量。

受益函数

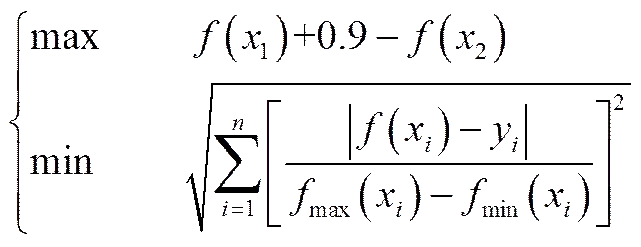
第1个式子为决策者1的受益函数，其中(1)为热效率的预测值，(2)为NO排放量的预测值，该公式表示热效率最大同时NO值最小；第2个式子为决策者2的受益函数，其中=2，(1)、(2)分别代表热效率和NO排放量的预测值，12代表其对应的期望值，max、min分别代表相对应的最大和最小值，该公式借鉴标准化欧氏距离，表示热效率和NO排放量二者离理想值的距离最近。其中两个公式中涉及到的数值均指归一化后的数据。

策略集：(1)，(2)∈[0.1,0.9]。

其中，决策1的过程为：第1步以受益函数1为目标函数先对进行寻优，此时(NO)的初始值取策略集中的随机值，第2步将之前寻优得到的作为给定值，以受益函数2为目标函数对(NO)进行寻优，得到的值作为给定值用于下一步的寻优过程中。决策2的过程则为：第1步中在策略集中取随机值，以受益函数1为目标函数对(NO)寻优，其他步骤与决策1过程类似，整个过程与决策1对称。两个决策进程中对两个目标不断寻优，直到无法再寻找到最优解时跳出循环，其中交换受益函数即是交换博弈策略的过程，整个博弈过程可参考图4。

所有的寻优过程由DE完成，其种群数设为30，迭代20次，采用自适应缩放因子、交叉因子策略，以及共享函数机制，share根据经验法设为0.5。作为理论分析，博弈交叉次数设为1，则得到的NASH均衡解集中解的个数为2。

2.3 优化结果

对工况3（炉效偏低，侧重于炉效的优化）、工况25（NO值较高，侧重于NO值优化）寻优前后进行具体分析，结果如表4所示。

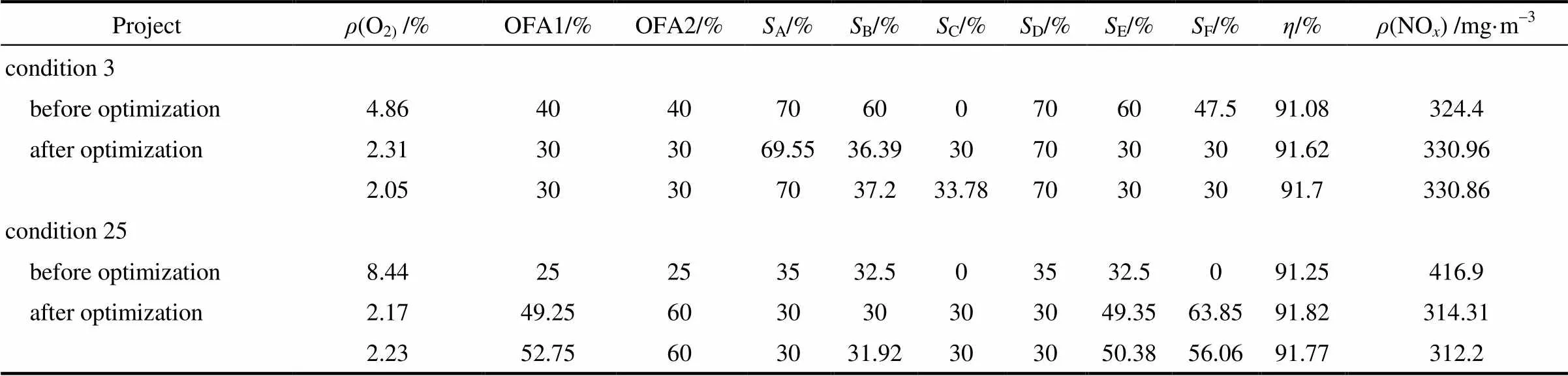
表4 优前后参数对比

由表4可知，工况3经优化后氧量降低，符合低氧燃烧技术，避免产生高温高氧区，可使燃烧更充分，一定程度上提高热效率且降低NO排放，燃烬风风门开度下降，有助于提高燃烧热效率，但不利于控制较低的NO浓度，优化后下层二次风风门开度（AD）基本保持不变，中间层二次风风门开度（BE）较大幅度减小，上层二次风风门开度（CF）一定幅度地增大，二次风为正宝塔配风方式，风门开度大小有所调整，这种配风方式有助于煤粉与空气充分混合，易燃尽，提高燃烧效率，但会导致NO的排放量升高，优化后炉效平均提高了0.58%，但NO排放量平均升高了6.51 mg·m-3，通过牺牲少部分NO排放量为代价来提高燃烧效率；工况25经优化后氧量降低，进行低氧燃烧，燃烬风增加，有助于降低NO排放[28]，优化后下层二次风风门开度（AD）稍微减小，中间层二次风风门开度（BE）一定幅度的增加，上层二次风风门开度（CF）较大幅度增加，二次风为倒宝塔配风方式，燃料燃烧火焰中心上移，主燃区温度降低而燃尽区温度升高，有利于抑制氮氧化物的生成[29]，优化后炉效平均提高了0.54%，NO排放量平均降低了103.64 mg·m-3，降幅达到24.86%。

3 600 MW燃煤炉的燃烧优化

3.1 600 MW燃煤锅炉的建模仿真

为验证本文提出的建模与优化方法的适用性，对文献[30]中提供的一台600 MW四角切圆燃煤锅炉12组相关数据进行仿真。首先建立和文献中完全相同的预测模型以增加本文提出的LSSVM-QGA与文献中采用的方法的对比效果，选取燃料量（）、总空气量（0）、各二次风门开度（AAABBCCDDEEF）、各燃烬风门开度（OFA1、OFA2）、各磨煤机通风量（mAmBmCmDmE）、各给煤机开度（mAmBmCmDmE）、碳基(ar)、氧基(ar)、氮基(ar)、氢基(ar)、低位发热量(net,ar)、水分(ar)、挥发分(ar)和燃烧器摆角（rsq）共28个参量作为输入，以NO排放量（(NO)）、飞灰含碳量（fh）和氧量（(O2)）3个参量作为输出，并根据文献[31]中的计算模型得到热效率的计算值。其中，预测模型的结构示意图如图7所示。

为对比效果，同样以第1～11组数据作为训练样本，以第12组数据作为测试样本进行仿真，仿真效果如图8～图10所示。

文献[30]中通过SVM建立了多输出预测模型，SVM的罚系数和核函数系数通过网格搜索法得到，该方法需不断调整寻优范围且只能搜索到最优参数组合范围，却并不能确定到最优值，而使用QGA算法寻找LSSVM的和只需设定一次寻优范围（0.001～500），智能性更高且寻优效果更好。

由图8～图10可知，LSSVM-QGA模型对NO排放量、飞灰含碳量和排烟氧量的拟合效果和预测效果很好，基本和样本数据曲线完全拟合。具体的仿真结果如表5所示。表中的SVM模型输出结果为文献[30]中的仿真结果，max、max分别指预测结果中出现的最大绝对误差和最大相对误差。

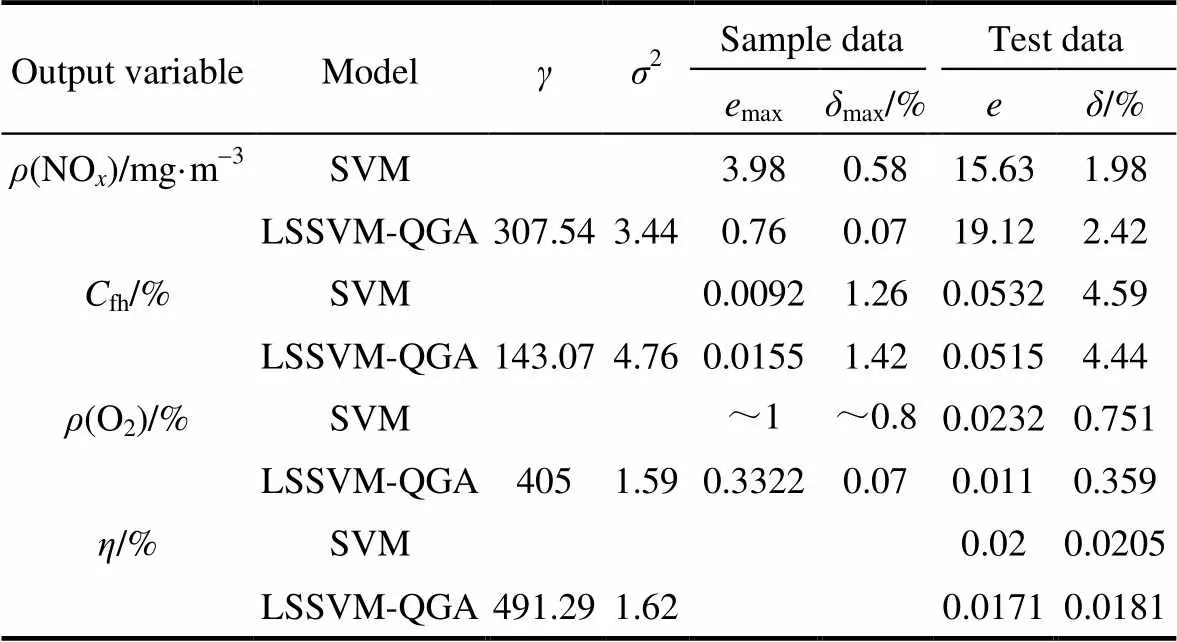
表5 600 MW锅炉LSSVM-QGA和SVM预测效果对比

由表可知，本文所提出的LSSVM-QGA模型对训练样本中各输出变量的预测结果中，只有fh的max和max稍大，但从图7可以看出，其各个训练样本的误差均较小，基本和样本数据曲线完全拟合，而算法对(NO)、(O2)和的预测效果则均优于SVM模型，说明本文所建立的模型有较好的拟合效果；从LSSVM-QGA模型对测试样本的预测效果来看，(NO)的预测偏差稍大，这可能是由于训练样本较少，或单工况预测偶然出现的结果，且2.42%的绝对误差在实际工程应用中完全可以接受，然而LSSVM-QGA模型对其他各输出变量的预测结果均优于SVM，说明本文所建立的模型的预测精度较高。

文献[30]中提到SVM确定参数和后建模过程在1 s左右，而LSSVM确定和后的建模只需要0.08 s左右，因此更加适合在线预测。

通过对比可知，LSSVM-QGA模型针对不同的研究对象，同样具有很好的泛化能力和预测效果，并且能够更加快捷准确地用于在线建模。

3.2 600 MW燃煤锅炉的多目标优化

参照文献[30]，以600 MW机组配套锅炉为研究对象，选取总空气量（1）、6个二次风门开度（2～7）、2个燃烬风门开度（8、9）和燃烧器摆角（10）共10个变量作为运行工况优化变量，各变量的寻优范围如下

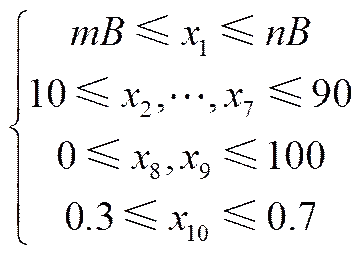
式中，=9、=11.5，分别为最小和最大风煤比，表示燃料量。

针对锅炉高热效率和低NO排放量的多目标优化问题，以工况12为例，采用博弈差分算法对优化变量进行最佳参数组合寻优，整个博弈优化的过程设置可参考2.2节中燃烧优化的实现，多目标优化的结果如表6所示。

表6 600 MW锅炉优化前后参数对比

表中优化前的数据指工况12的样本数据，优化后的数据分别为[30]中不断调整权值分配后经PSO算法寻优的最佳优化调整值，和经博弈差分算法寻优后的运行工况最佳参数组合。由表可知，与PSO寻优结果相比，经NASH均衡优化后总空气量少量减少，二次风配风接近缩腰配风，这种配风更有助于创造缺氧环境进而抑制NO的生成，而前者二次风配置类似均等配风，燃烬风门开度有所增加并且燃烧器摆角幅度较大，这与前者趋势一致。总的优化结果说明NASH均衡优化对风煤比和燃料的混合状态进行了调整，有利于改善燃烧效果，降低NO排放。

经NASH均衡优化的方法与PSO优化结果相比较可知，两者优化后的热效率均为94.25%左右，优化效果并不明显，由于94.31%的热效率已经很高，提升空间不大，所以优化后的参数组合主要针对降低NO的排放量，两者优化后的NO值分别为732.53 mg·m-3和725.23 mg·m-3，前者稍高的原因应该是由于LSSVM-QGA模型对该工况的预测存在的误差导致，并且工程应用中该误差在允许的范围内。经对比，两种方法的优化效果基本一致，然而文献[30]中优化方案的确定是经过人为主观地不断进行权值调整和效果分析得到的，这费时费力显然不利于现场工程应用，而本文所提出的NASH均衡优化方法则只需要两个受益函数的互相博弈即可实现，智能性更高，体现出该方法具有更强的适用性和先进性。虽然该方法涉及到的算法较多，理论复杂度较高，但通过将不同的算法封装成工具箱进而在MATLAB中调用，可以降低方法的复杂度、加快算法的运行速度并最终增强该方法实现的可行性。

4 结 论

针对电站锅炉燃烧特性的建模与优化问题，在最小二乘支持向量机算法中加入量子遗传算法，提高了算法的预测效果；通过加入共享函数机制得到一种改进的自适应差分进化算法，并使用这种算法演化博弈论中NASH均衡以达到锅炉燃烧优化的最优解。本文首次将博弈均衡策略引入电站锅炉燃烧的多目标优化问题中，并实现了对电站锅炉运行工况的均衡优化，通过不同案例的仿真结果证明了该方法改善了人为主观地分配权值的弊端，最终得到的最优解集有助于现场工况调整，更适合于复杂多变的电站锅炉运行过程，有助于使电站锅炉达到高效低污染排放运行和提高电厂运营效益并实现节能减排，对电站锅炉的燃烧优化具有一定的指导意义。

References

[1] 刘炯天. 关于我国煤炭能源低碳发展的思考[J]. 中国矿业大学学报(社会科学版), 2011, 13(1): 5-12. LIU J T. Reflection on low-carbon development of coal energy in China[J]. Journal of China University of Mining&Technology (Social Sciences), 2011, 13(1): 5-12.

[2] QIN S J, BADGWELL T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 11(7): 733-764.

[3] HAISSIG C M, WOESSNER M A, PIROVOLOU D K. Adaptive fuzzy controller that modifies membership functions: US5822740 A[P]. 1998.

[4] 王占能, 徐祖华, 赵均, 等. 基于负荷划分数据和支持向量机的火电厂燃烧过程建模[J]. 化工学报, 2013, 64(12): 4496-4502. WANG Z N, XU Z H, ZHAO J,. Coal-fired power plant boiler combustion process modeling based on support vector machine and load data division [J]. CIESC Journal, 2013, 64 (12): 4496-4502.

[5] 许昌, 吕剑虹, 郑源, 等. 以效率和低NO排放为目标的锅炉燃烧整体优化[J]. 中国电机工程学报, 2006, 26(4): 46-50. XU C, LÜ J H, ZHENG Y,. A boiler combustion global optimization on efficiency and low NOemissions object[J]. Proceedings of the CSEE, 2006, 26(4): 46-50.

[6] 方海泉, 薛惠锋, 李宁, 等. 基于贝叶斯神经网络遗传算法的锅炉燃烧优化[J]. 系统仿真学报, 2015, 27(8): 1790-1795. FANG H Q, XUE H F, LI N,. Boiler combustion optimization based on Bayesian neural network and genetic algorithm [J]. Journal of System Simulation, 2015, 27(8): 1790-1795.

[7] 孙卫红, 童晓, 李强. 改进PSO优化参数的LSSVM燃煤锅炉NO排放预测[J]. 数据采集与处理, 2015, 30(1): 231-238. SUN W H, TONG X, LI Q. NOemission concentration of coal-fired boiler prediction based on improved PSO parameter optimized LSSVM[J]. Journal of Data Acquisition and Processing, 2015, 30(1): 231-238.

[8] 高芳, 翟永杰, 卓越, 等. 基于共享最小二乘支持向量机模型的电站锅炉燃烧系统的优化[J]. 动力工程学报, 2012, 32(12): 928-933. GAO F, ZHAI Y J, ZHUO Y,. Combustion optimization for utility boiler based on sharing LSSVM model[J]. Power Engineering, 2012, 32(12): 928-933.

[9] 艾娜, 吴作伟, 任江华. 支持向量机与人工神经网络[J]. 山东理工大学学报(自然科学版), 2005, 19(5): 45-49. AI N, WU Z W, REN J H. Support vector machine and artificial neural network[J]. Journal of Shandong University of Technology(Sci. & Tech.), 2005, 19(5): 45-49.

[10] 阎威武, 邵惠鹤. 支持向量机和最小二乘支持向量机的比较及应用研究[J]. 控制与决策, 2003, 18(3): 358-360. YAN W W, SHAO H H. Application of support vector machines and least squares support vector machines to heart disease diagnoses[J]. Control & Decision, 2003, 18(3): 358-360.

[11] 吕玉坤, 彭鑫, 赵锴. 电站锅炉热效率和NO排放混合建模与优化[J]. 中国电机工程学报, 2011, 31(26): 16-22. LÜ Y K, PENG X, ZHAO K. Hybrid modeling optimization of thermal efficiency and NOemission of utility boiler[J]. Proceedings of the CSEE, 2011, 31(26): 16-22.

[12] 刘波, 王凌, 金以慧. 差分进化算法研究进展[J]. 控制与决策, 2007, 22(7): 721-729. LIU B, WANG L, JIN Y H. Advances in differential evolution[J]. Control & Decision, 2007, 22(7): 721-729.

[13] 纳什. 纳什博弈论论文集[M]. 张良桥, 王晓刚, 译. 北京: 首都经济贸易大学出版社, 2000: 30-49. NASH J R. Essays of Game Theory[M]. ZHANG L Q, WANG X G, trans. Beijing: Capital University of Economics & Business Press, 2000: 30-49.

[14] SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.

[15] ESEN H, OZGEN F, ESEN M,. Modelling of a new solar air heater through least-squares support vector machines[J]. Expert Systems with Applications, 2009, 36(7): 10673-10682.

[16] PARDO M, SBERVEGLIERI G. Classification of electronic nose data with support vector machines[J]. Sensors & Actuators B Chemical, 2005, 107(2): 730-737.

[17] CAI Z, XU W, MENG Y,. Prediction of landslide displacement based on GA-LSSVM with multiple factors[J]. Bulletin of Engineering Geology & the Environment, 2016, 75(2): 637-646.

[18] GORJAEI R G, SONGOLZADEH R, TORKAMAN M,. A novel PSO-LSSVM model for predicting liquid rate of two phase flow through wellhead chokes[J]. Journal of Natural Gas Science & Engineering, 2015, 24(1): 228-237.

[19] 顾燕萍, 赵文杰, 吴占松. 基于最小二乘支持向量机的电站锅炉燃烧优化[J]. 中国电机工程学报, 2010, 30(17): 91-97. GU Y P, ZHAO W J, WU Z S. Combustion optimization for utility boiler based on least square support vector machine[J]. Proceedings of the CSEE, 2010, 30(17): 91-97.

[20] 梁昌勇, 柏桦, 蔡美菊, 等. 量子遗传算法研究进展[J]. 计算机应用研究, 2012, 29(7): 2401-2405. LIANG C Y, BAI H, CAI M J,. Advances in quantum genetic algorithm[J]. Application Research of Computers, 2012, 29(7): 2401-2405.

[21] 钱志永. 锅炉冷、热态性能试验及计算软件开发[D]. 南京: 东南大学, 2003. QIAN Z Y. The cold and hot performance test of boiler and development of calculation software[D]. Nanjing: Southeast University, 2003.

[22] 徐磊, 陈宪麦. 轨道不平顺作用下铁路列车车体振动状态的PCA-SVM预测分析[J]. 铁道学报, 2014, (7): 16-23. XU L, CHEN X M. PCA-SVM forecast of car-body vibration states of railway locomotives and vehicles under the action of railway action of tracy irregularities[J]. Journal of the China Railway Society, 2014, (7): 16-23.

[23] 沈芳平, 周克毅, 胥建群, 等. 锅炉效率计算模型的分析与比较[J]. 锅炉技术, 2004, 35(1): 48-52. SHEN F P, ZHOU K Y, XU J Q,. Analysis and comparison on calculation pattern of boiler efficiency[J]. Boiler Technology, 2004, 35(1): 48-52.

[24] 刘金琨. 智能控制[M]. 3版. 北京: 电子工业出版社, 2014: 248-252. LIU J K. Intelligent Control [M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2014: 248-252.

[25] WANG J, YI W U, PERIAUX J. Decentralized multi-point optimization algorithms for multi-airfoil design in aerodynamics[J]. Journal of Astronautics, 2003, 24(1): 71-77.

[26] 黄涛. 博弈论教程[M]. 北京: 首都经济贸易大学出版社, 2004: 9-33. HUANG T. A Course of Game Theory and Its Applications[M]. Beijing: Capital University of Economics & Business Press, 2004: 9-33.

[27] BISWAS S, DAS S, KUNDU S,. Utilizing time-linkage property in DOPs: an information sharing based Artificial Bee Colony algorithm for tracking multiple optima in uncertain environments[J]. Soft Computing, 2014, 18(6): 1-14.

[28] 王为术, 刘军, 王保文, 等. 超临界锅炉劣质无烟煤燃烧NO释放特性的数值模拟[J]. 煤炭学报, 2012, 37(02): 310-315. WANG W S, LIU J, WANG B W,. Numerical simulation on the NOrelease characteristics during the combustion of poor-quality anthracite in supercritical boiler[J]. Journal of China Coal Society, 2012, 37(2): 310-315.

[29] 张晓辉, 孙锐, 孙绍增, 等. 立体分级燃烧对NO排放特性的影响[J]. 机械工程学报, 2009, 45(2): 199-205. ZHANG X H, SUN R, SUN S Z,. Effects of stereo-staged combustion technique on NOemission charactisctics[J]. Chinese Journal of Mechanical Engineering, 2009, 45(2): 199-205.

[30] 尹凌霄. 电站燃煤锅炉燃烧优化的智能技术研究[D]. 南京: 东南大学, 2014. YIN L X. Research on combustion optimization for coal-fired utility boiler based on smart technology[D]. Nanjing: Southeast University, 2014.

[31] 李智, 蔡九菊, 曹福毅, 等. 电站锅炉效率在线计算方法[J]. 节能, 2005, (3): 28-29. LI Z, CAI J J, CAO F Y,. Online calculation method for power station boiler efficiency[J]. Energy Conservation, 2005, (3): 28-29.

Equilibrium optimization for high efficiency and low pollution combustion of power-generation boilers using game differential evolution algorithm

ZHAO Minhua1, HU Yi1, LI Jin2, WANG Yusheng1, WU Rui1, SONG Le1

(1School of Information and Control Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, Shaanxi, China;2Xi’an IBL Technology Co., Ltd., Xi’an 710065, Shaanxi, China)

Improving thermal efficiency and reducing pollutant emissions such as NOis a critical problem to be solved for conservation and emission reduction in power plant energy. A combustion optimization model was established by quantum genetic algorithm (QGA) optimized least squares support vector machine (LSSVM-QGA). The model predicted boiler thermal efficiency and NOemissions at average relative error of 0.054% and 1.229%, respectively, which demonstrated high prediction accuracy, generalization ability and applicability. Based on the model, a method of differential evolution algorithm (DE) of self-adaptive scaling/crossover factors and sharing function followed by evolutionary Nash equilibrium was proposed for multi-objective optimization of boiler’s combustion. Results show that optimization method based on NASH equilibrium can get optimal set of solutions to operational variables, which improve operating conditions and keep power generation boiler at a stable equilibrium state of combustion.

utility boiler; optimization; least square support vector machine; model; prediction; differential evolution algorithm; NASH equilibrium

10.11949/j.issn.0438-1157.20161480

TP 273；TK 227.1

A

0438—1157（2017）06—2455—10

胡毅。

赵敏华（1971—），女，副教授。

国家自然科学基金青年科学基金项目(51508446)；陕西省自然科学基金项目(2015JM6337)。

2016-10-19收到初稿，2017-02-07收到修改稿。

2016-10-19.

HU Yi, whoyee@163.com

supported by the National Natural Science Foundation of China (51508446) and the Natural Science Foundation of Shaanxi Province (2015JM6337).