基于重构的半监督ELM及其在故障诊断中的应用

易维淋，田学民，张汉元



基于重构的半监督ELM及其在故障诊断中的应用

易维淋，田学民，张汉元

（中国石油大学（华东）信息与控制工程学院，山东青岛266580）

工业过程中获取带标签的故障数据困难，而无标签故障数据却大量存在，如何有效地利用数据信息进行故障诊断是故障诊断领域的重要内容。为更充分地挖掘和利用数据信息，提出一种新的半监督学习方法：基于重构的半监督极限学习机(RSELM)。相比于传统的半监督极限学习机(ELM)方法，RSELM采用自动编码ELM(ELM-AE)获得的输出权重替代随机的隐含层输入权重，能更有效地提取数据特征；考虑到数据均可由其近邻数据来线性重构，故可构建近邻数自适应选择的重构图，并同时利用数据的标签信息优化连接权重，以更优地反映数据结构信息；通过建立新的含局部保持的目标函数，可有效地训练分类器。标准数据集和TE过程上的仿真实验验证了所提算法的有效性。

半监督极限学习机；重构；ELM-AE；故障诊断

引 言

随着工业过程安全性和可靠性需求的增加，故障诊断技术受到广泛的关注[1-5]。而工业过程中对历史故障数据进行人工标注是费时费力的，因而如何有效地利用有限的带标签故障数据进行故障分类，确定故障类型成为了故障诊断领域的一个重要内容。

极限学习机(ELM)是Huang等提出的一种学习速度快且泛化性能好的单隐层前馈神经网络（SLFNs）训练方法[6-7]，已被广泛地应用于数据的分类、聚类、回归分析、特征选择和表征学习等领域[8-16]。例如，通过对每个样本施以不同的误分类代价，Zong等[17]提出WELM以解决不平衡数据的分类问题；Kasun等[18]利用自动编码技术将原输入数据作为输出目标，提出自动编码极限学习机(ELM-AE)，通过将获得的输出权重代替随机确定的隐含层的输入权重，可更有效地提取数据特征。鉴于ELM的快速有效性，ELM也被应用于故障诊断领域[19-21]。

然而，ELM是一种监督型的学习方法，而现实中获取带标签数据困难，无标签数据却大量存在。为有效地利用无标签数据来提高学习性能，学者们基于成对样本间相似性建立反映数据结构信息的kNN图，并将局部结构保持函数融入原ELM的目标函数，提出了各种半监督ELM方法[22-26]。Liu等[22]提出一种半监督ELM方法并将之应用于室内定位；Iosifidis等[23]融入数据的判别信息，给出了用于单角度和多角度动作识别的半监督学习方法，即SDELM和MVSDELM；Huang等[24]则利用图论和谱回归理论提出了一种有效的半监督分类方法SELM；而Zhou等[25]则同时考虑了数据的流型特征和成对约束问题，给出了一种快速有效的半监督ELM方法；Averdi等[26]则通过将集成的ELM算法推广至半监督学习领域，并结合空间正则化，提出半监督ELM方法并将之应用于高光谱图像分类与分割。

尽管上述方法能有效地完成半监督学习任务，但在挖掘和利用数据信息方面还有待进一步研究。

（1）数据特征信息的提取：随机确定的隐含层参数使得数据在映射至特征空间的过程中对数据的潜在特征信息提取不充分。

（2）数据结构信息的反映：数据的结构信息是通过构建kNN图来反映的，但存在以下两个问题。

① kNN图是根据经验给每个样本点设定相同的近邻数来建立的，近邻数的选择独立于数据分布，使得在对样本数据进行学习的过程中影响标签信息的传播；

② kNN图中，确定衡量样本间相似性的权重时，仅利用了数据间的距离信息，而忽略了带标签数据的标签(类别)信息。

为解决传统的半监督ELM存在的问题，利用ELM-AE在提取数据特征方面的优势以及局部线性嵌入(LLE)[27]具有的局部结构保持功能，本文提出一种基于重构的半监督ELM方法，即RSELM。RSELM采用ELM-AE获取的输出权重代替随机确定的隐含层权重，提取数据特征；基于LLE中样本数据均可由其近邻点加权重构的思想，在特征空间中建立反映数据局部结构信息的自适应重构图，并利用数据类别信息优化连接权重，同时在输出空间中构建局部结构保持的目标函数，基于此来训练分类器。基于RSELM的标准数据集分类和TE过程的故障诊断实验验证了所提算法的有效性。

1 相关工作

1.1 自动编码极限学习机

与传统的监督型学习算法ELM不同，自动编码极限学习机(ELM-AE)[18]采用无监督的学习策略，将输入数据作为输出目标，得到的输出权重可有效地用于数据特征的提取。

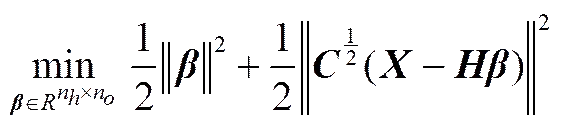
通过对式(1)求解，则可得到输出权重为

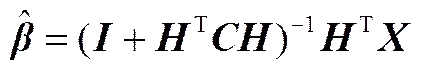
1.2 半监督极限学习机

基于光滑性假设思想，半监督ELM(SELM)[24]利用成对数据的相似关系构建拉普拉斯图，建立含流形正则项的优化目标函数，以同时利用带标签和无标签数据信息来处理实际中带标签数据不足而无标签数据大量存在的情况，提高分类器性能。

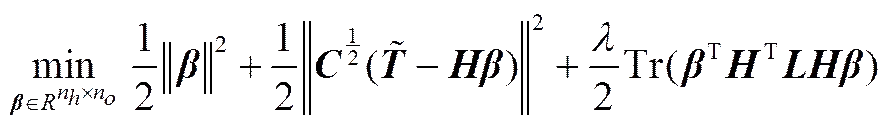
(4)

式中，为样本数据与之近邻数据间距离的均值。

与经典的ELM一致，SELM采用随机映射将数据映射至特征空间，对数据的潜在信息提取不充分；同时SELM利用成对样本间的相似关系建立kNN图来反映数据结构，但每个样本点选取的近邻数却是独立于数据结构而根据经验选择的。而对于式(4)所示衡量成对样本间相似程度的权重w的确定，仅利用了数据间的距离信息，却未能对带标签数据的先验的类别信息加以利用。

2 基于重构的半监督极限学习机

LLE[27]是一种能够使降维后的数据保持原有局部结构的非线性降维方法，其主要思想为数据的重构：输入/输出空间中，每个样本数据均可通过对其近邻数据加权来线性重构，而权重大小即可反映数据间的相似程度，为此，数据间的局部结构信息可通过建立一个重构图的方式来表达。而半监督学习的一种形式即为：利用数据间的局部结构信息来弥补带标签数据不足，故本文提出基于重构的半监督极限学习机(RSELM)，通过构建自适应重构图来表征数据结构，建立新的局部保持目标函数来进行分类器的训练，以处理标记数据过少的情况。

不同于LLE的是，在构建重构图的过程中，LLE根据经验给每个样本确定相同的近邻数，基于重构误差最小的准则来确定重构图的连接权重。而RSELM则通过数据的距离信息和类别信息来确定重构图的连接权重，基于重构误差最小的准则来自适应地确定每个样本的近邻数，使得重构图的构建依赖于数据分布，更好地反映数据结构信息。

如图1所示，RSELM方法具体可分为3步：（1）采用ELM-AE方法确定隐含层的输入权重，将原数据映射至特征空间；（2）特征空间中，通过最小化每个样本数据的相应隐含层输出的重构误差，自适应地选择每个样本的近邻数来建立反映数据结构信息的加权图，即重构图；（3）输出空间中，为保持原数据的结构信息，则每个样本的输出均应能够由其近邻点的相应输出来进行较小误差的重构，基于此可构建含有重构误差项的目标函数来对网络进行训练，得到满足要求的半监督分类器。

2.1 构建重构图

特征空间中，每个样本点均可由其近邻点来线性重构，其重构误差为

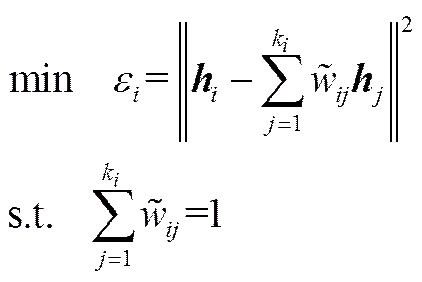
其中，k表示对应于样本的隐含层输出的近邻数，且，隐含层参数由ELM-AE算法确定(图1)。

（1）若样本数据均为带标签数据且属于同类则增大其权重(同类样本相似性大)；

（2）若样本数据均为带标签数据但不属于同类则减小其权重（不同类样本相似性小）；

（3）若样本数据中含有无标签数据则保持其权重不变，具体如式(6)所示

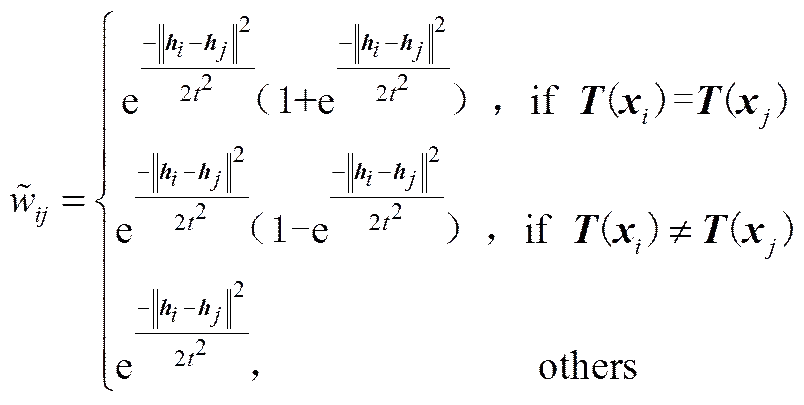
其中，()样本对应的所属类的标签，为样本数据隐含层输出与之近邻间距离的均值。

值得注意的是：（1）构建的重构图是带方向的自适应kNN图，即衡量相似程度的权重；（2）样本间权重的计算是在ELM特征空间中而不是输入空间中进行的，因为在空间中输入数据间的非线性关系能更好地表达。

对式(5)所示的重构误差函数进行最小化，即可得到每个样本的自适应近邻数。由于式(5)所示的最小化问题并非凸优化问题，故难以寻找到该问题的最优解。本文采用在一定近邻数范围内进行遍历的方法来寻找相对最优的近邻数，考虑到计算问题，本文所选取的最大近邻数max为10。

2.2 RSELM算法

ELM特征空间中，通过建立自适应的重构图来反映数据的局部结构信息；输出空间中，则可构建局部保持的目标函数，使得输入空间中每个样本的对应的输出均可由其近邻点对应输出以相同的权重进行小误差重构，即

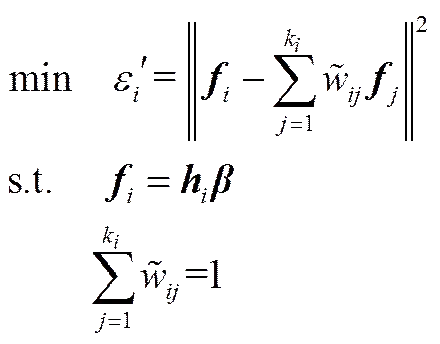
式中，′是样本对应网络输出的重构误差。

将约束条件代入目标函数则有

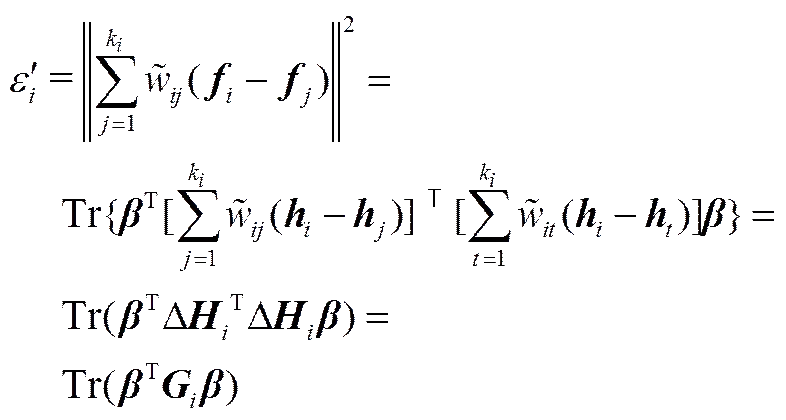
由式(5)和式(8)对比可以看出，=Tr()，即样本在输出空间中的重构误差是与ELM特征空间中的样本重构误差密切相关，故若使得式(7)所示的目标函数最小，则可认为数据的局部结构信息被较好地保留下来。

引入新的局部保持函数的RSELM的优化目标即为找到输出权重，使得以下目标函数最小

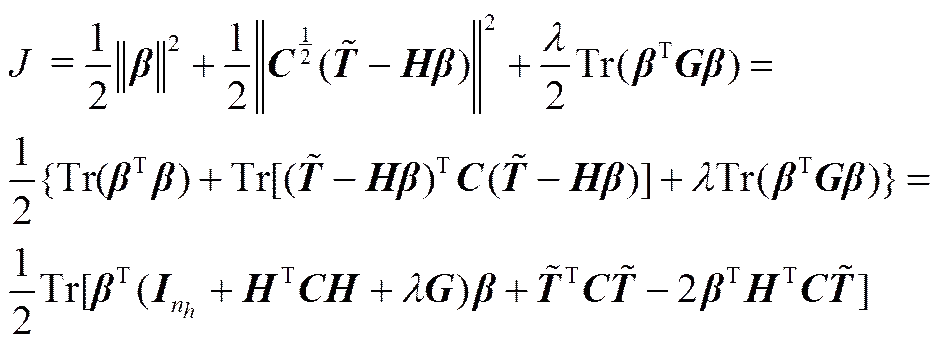
式中，为相应于每个样本训练误差的惩罚因子；为权衡参数；为样本的平均重构偏移。

为得到满足目标函数的输出权重值*，令，可得输出权重为

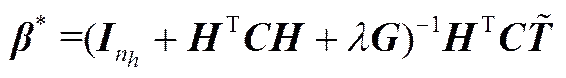
则对于新样本的相应网络输出为

(11)

而样本所属的类为RSELM分类器输出值最高的输出节点所代表的标签类。令y()表示第个输出节点的输出值，则样本所属的类标签为

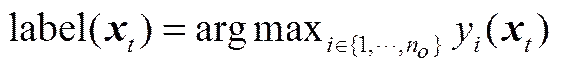
以二分类问题为例，传统的SELM网络和RSELM的局部保持结构示意图如图2和图3所示。为便于比较，假定RSELM在特征空间中的数据分布与SELM在输入空间中一致。由图可知，样本点A和C属于正类样本，B和D属于负类样本。映射前，根据近邻规则，对于SELM，样本点A和B的近邻数均独立于样本的分布给定为A=B=5，而RSELM却可基于最小化重构误差的准则根据样本的分布自适应的选择近邻数(A=5,B=4)；映射后，SELM能较好地保持原数据结构，即A、B、C、D的距离基本保持不变；而RSELM在考虑了数据的类别信息，对连接权重优化后，可使得输出空间中的同类样本间的距离减小(B和D)，不同类样本间的距离增大(A和D，B和C)，更有利于数据的分类。

图2 SELM局部结构保持示意图

Fig.2 Local structure preserving graph of SELM

3 基于RSELM的故障诊断

基于RSELM的故障诊断方法由离线建模和在线诊断两部分组成。离线建模是通过历史的标签与未标签故障数据建立故障诊断模型；而在线诊断则是对新到的故障数据进行诊断分类，以便于判断故障类型。

离线建模

输出：网络的输出权重*。

（1）归一化数据集为均值为0，方差为1的标准数据集；

（2）初始化隐含层节点数n，根据ELM-AE确定隐含层参数，计算隐含层输出；

（3）ELM特征空间中，建立重构图：

①计算样本间距离找到样本,=1,…,+的max个最近邻，计算初始权重；

③得出样本的最终近邻数k，使最小；

（4）计算平均重构偏移；

（5）选择平衡参数和，计算输出权重*。

在线诊断

输出：未知样本所属的类。

（1）根据训练集的均值和方差归一化为标准数据集；

（2）根据已有的输入权重和偏差，计算隐含层输出；

（3）基于输出权重*计算网络输出；

（4）根据式(12)确定每个样本所属的类，即确定故障类型。

4 仿真实验

为验证所提算法的有效性，分别采用源自KEEL数据库(http://www.keel.es/datasets.php)用于半监督分类的5个标准数据集G50C[29-30]、Iris、Wine、Image segmentation[24]、Vowel[20]以及TE过程作为仿真对象，在MATLAB中分别将SDELM[23]、SELM[24]与本文的RSELM的方法进行比较。

参数设置：随机选取每个数据集的80%作为训练集，其余作为测试集。训练集又分为带标签数据集、无标签数据集和验证集，其中验证集为训练集的10%，且仅用于网络模型参数和的选择。而所用方法的隐含层节点数均设为2000，SDELM和SELM的近邻数均设为5，RSELM的最大近邻数设为10，而平衡参数和则在指数序列{10-3,10-2,…,104}基于验证集的分类精度进行选取。

仿真过程中，定义数据的标记率为=/(+)，其中，表示带标签样本数，表示无标签样本数，表示验证集样本数，表示测试集样本数。分类精度即被正确分类的样本数/测试样本总数。

4.1 标准数据集仿真

采用源自KEEL数据库用于半监督分类的标准数据集G50C、Iris、Wine、Vowel和Image segmentation作为仿真对象，仿真过程中，选择数据标记率0.2，具体数据信息如表1所示。

由于隐含层参数随机选取导致网络输出不稳定的原因，各方法均独立运行20次，取其“均值±标准差”作为对比，仿真结果如表2所示。

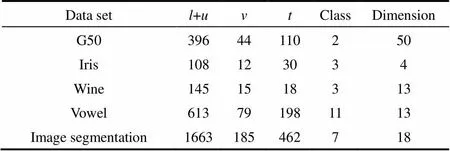
表1 标准数据集信息

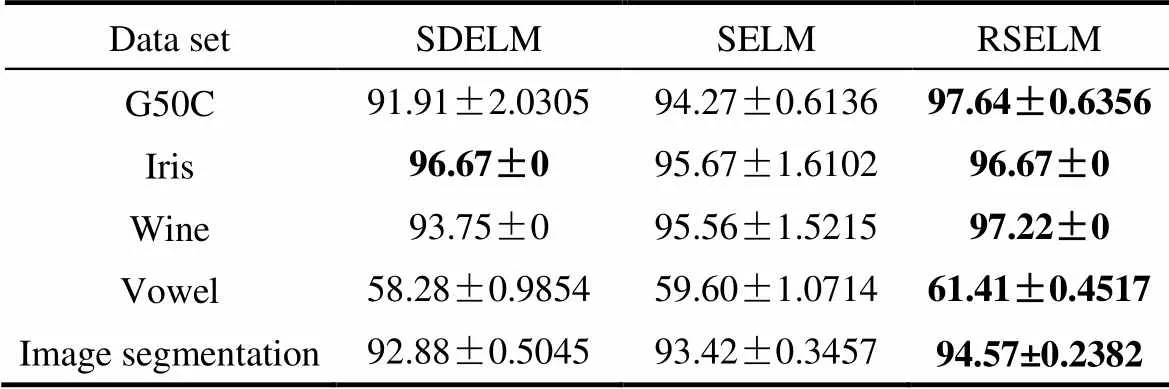
表2 标准数据集分类结果

由表2可以看出，相比于SDELM和SELM学习方法，RSELM能得到最优的分类结果，验证了算法的有效性，同时也说明了在带标签数据不足的情况下，所提方法能够更充分地挖掘和利用数据信息来完成半监督学习任务，提高网络的分类性能。

4.2 TE过程仿真

田纳西-伊斯曼(TE)过程[31]，是伊斯曼化学品公司的Downs和Vogel公布的用于学术研究的过程仿真，它基于实际化工过程，包含41个测量变量和12个操纵变量，有21种预设定的故障。每种故障工况的数据包均含960个样本，且均在第161个样本数据点加入故障，即每类故障均含有800个故障数据。目前，TE过程已经成为大家公认的用于检验各种控制及监控方案性能的研究对象。

仿真实验中，选取9种类型的故障数据，并将之混合作为故障数据集进行学习，每类故障数据均归一化为均值为0，方差为1的标准数据。

以标记率=0.2为例，说明RSELM在带标签数据不足的情况下进行故障诊断的有效性。各方法对所选取的9种故障的分类结果如表3和图4所示。其中，总体分类精度（overall accuracy）为所有正确分类样本数除以总的测试样本数。

表3 TE过程故障诊断结果()

Table 3 Results of fault diagnosis on TE process()/%

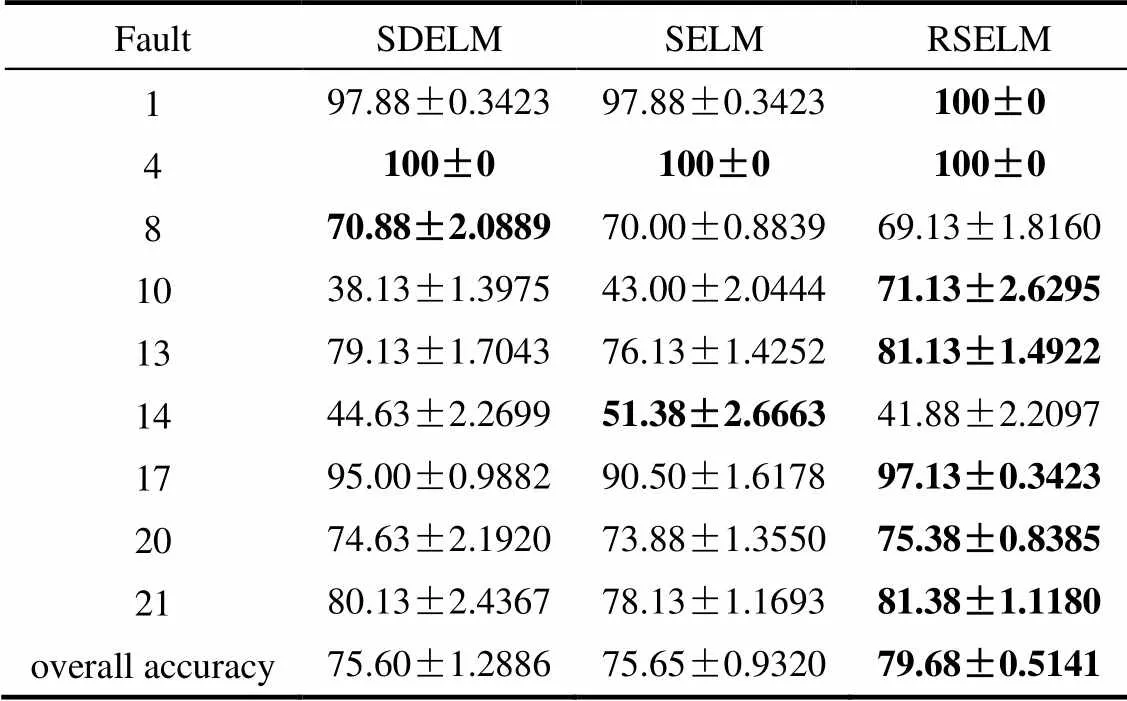
表3 TE过程故障诊断结果()

FaultSDELMSELMRSELM 197.88±0.342397.88±0.3423100±0 4100±0100±0100±0 870.88±2.088970.00±0.883969.13±1.8160 1038.13±1.397543.00±2.044471.13±2.6295 1379.13±1.704376.13±1.425281.13±1.4922 1444.63±2.269951.38±2.666341.88±2.2097 1795.00±0.988290.50±1.617897.13±0.3423 2074.63±2.192073.88±1.355075.38±0.8385 2180.13±2.436778.13±1.169381.38±1.1180 overall accuracy75.60±1.288675.65±0.932079.68±0.5141

由表3和图4可知，对于所列的故障类型，除故障8和故障14外，所提方法对于均能以最高的分类精度对故障进行分类，特别是对于故障10，RSELM的分类精度相比于其他两种方法提高了30%左右的分类精度。而故障8和故障14分类精度下降是因为分类器参数是根据验证集的总体分类精度来调整的，为达到更高的总体分类精度，分类器重心偏向了其他几种故障的精度的提高，但就总体分类精度来说，在=0.2时，总体分类精度提高了4%，说明了在相同的条件下，RSELM能够更有效地对故障进行分类，提高故障诊断性能。

为进一步验证算法的有效性，对不同数据标记率下的故障数据进行仿真。不同标记率下的总体分类精度（overall accuracy）如表4和图5所示。可以看出，随着样本数据的标记率的增大，各种方法的故障诊断精度呈现升高的趋势，而当带标签数据过少时(≤0.2)，RSELM的分类精度明显提升更多；而在相同的标记率下，RSELM总能得到比其他两种方法更高的总体分类精度，说明了RSELM在综合考虑了数据特征提取、自适应重构图和类别信息优化权重等因素的情况下，能更充分地挖掘和利用历史故障数据信息来训练半监督分类器，使得对于未知的故障数据，RSELM能更有效地对故障进行分类，提高故障诊断性能。

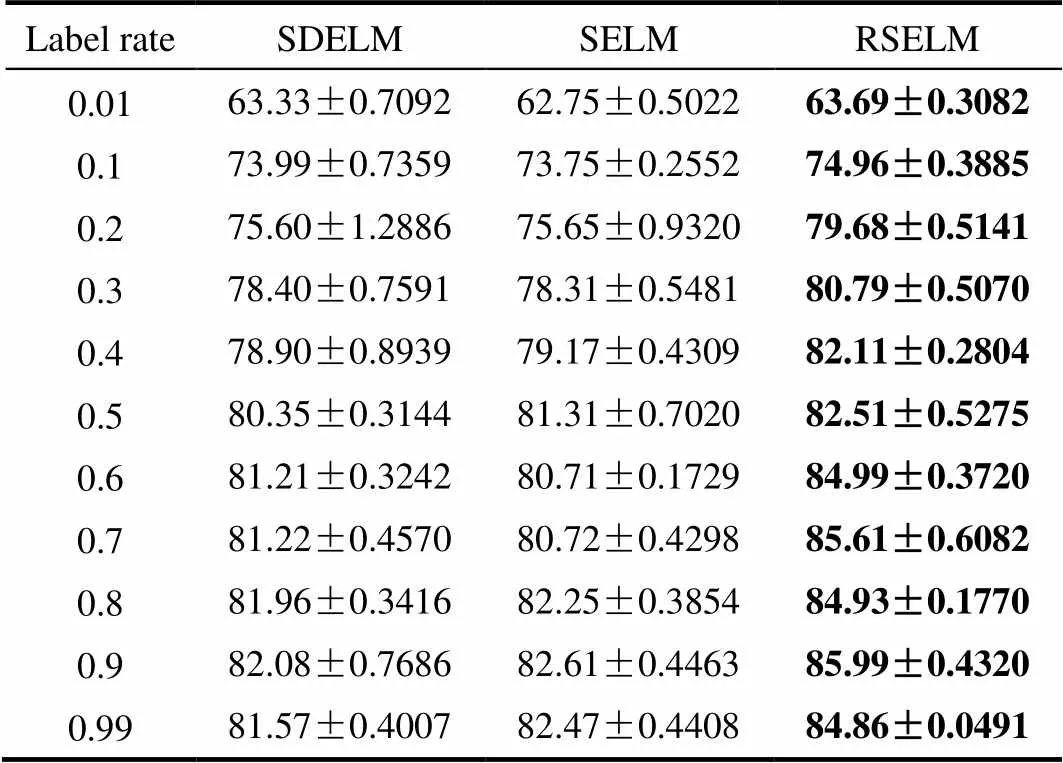
表4 TE过程不同标记率下故障诊断结果

5 结 论

本文提出了一种基于重构的半监督极限学习机(RSELM)方法，以更充分地挖掘和利用数据信息，来处理实际工业过程中获取带标签数据困难，而无标签数据大量存在的情况下的故障诊断问题。不同于传统的半监督ELM方法，RSELM利用ELM-AE获取的输出权重替代随机的输入权重以提取数据特征，并在特征空间中基于重构误差最小的准则构建图时，同时考虑了数据的局部结构信息和带标签数据的类别信息来优化连接权重，并基于此在输出空间中构建新的局部保持的目标函数来训练分类器。基于标准数据集和TE过程的仿真结果表明，所提算法能达到比传统的半监督ELM方法相近甚至更高的分类精度，可有效地提高故障诊断的准确性。

References

[1] GE Z, SONG Z, GAO F. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562.

[2] QIN S J. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control, 2012, 36(2): 220-234.

[3] ZHANG Y, MA C. Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS[J]. Chemical Engineering Science, 2011, 66(1): 64-72.

[4] 刘强, 柴天佑, 秦泗钊, 等. 基于数据和知识的工业过程监视及故障诊断综述[J]. 控制与决策, 2010, 25(6): 801-807. LIU Q, CHAI T Y, QIN S Z,. Progress of data-driven and knowledge-driven process monitoring and fault diagnosis for industry process[J]. Control & Decision, 2010, 25(6): 801-807.

[5] 李晗, 萧德云. 基于数据驱动的故障诊断方法综述[J]. 控制与决策, 2011, 26(1): 1-9. LI H, XIAO D Y. Survey on data driven fault diagnosis methods[J]. Control & Decision, 2011, 26(1): 1-9.

[6] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]// IEEE International Joint Conference on Neural Networks. Proceedings. IEEE Xplore, 2004, 2: 985-990.

[7] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489-501.

[8] HUANG G B, WANG D H, LAN Y. Extreme learning machines: a survey[J]. International Journal of Machine Learning & Cybernetics, 2011, 2(2): 107-122.

[9] GAO H, HUANG G B, SONG S,. Trends in extreme learning machines: a review[J]. Neural Networks the Official Journal of the International Neural Network Society, 2015, 61: 32.

[10] HUANG G B. An insight into extreme learning machines: random neurons, random features and kernels[J]. Cognitive Computation, 2014, 6(3): 376-390.

[11] HUANG G B, CHEN L, SIEW C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892.

[12] HUANG G B, CHEN L. Enhanced random search based incremental extreme learning machine[J]. Neurocomputing, 2008, 71(16/17/18): 3460-3468.

[13] HUANG G B, DING X, ZHOU H. Optimization method based extreme learning machine for classification[J]. Neurocomputing, 2010, 74(1/2/3): 155-163.

[14] HUANG G B, ZHOU H, DING X,. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), 2012, 42(42): 513-529.

[15] HUANG G B. An insight into extreme learning machines: random neurons, random features and kernels[J]. Cognitive Computation, 2014, 6(3): 376-390.

[16] CAMBRIA E, HUANG G B, KASUN L L C,. Extreme learning machines[J]. Intelligent Systems, IEEE, 2013, 28(6): 30-59.

[17] ZONG W, HUANG G B, CHEN Y. Weighted extreme learning machine for imbalance learning[J]. Neurocomputing, 2013, 101(3): 229-242.

[18] KASUN L L C, ZHOU H, HUANG G B,. Representational learning with ELMs for big data[J]. Intelligent Systems IEEE, 2013, 28(6): 31-34.

[19] MARTINEZ-REGO D, FONTENLA-ROMERO O, PEREZ- SANCHEZ B,. Fault Prognosis of Mechanical Components Using On-Line Learning Neural Networks[M]// Artificial Neural Networks – ICANN 2010. Berlin , Heidelberg: Springer, 2010: 60-66.

[20] MUHAMMAD I G, TEPE K E, ABDEL-RAHEEM E. QAM equalization and symbol detection in OFDM systems using extreme learning machine[J]. Neural Computing and Applications, 2013, 22(3): 491-500.

[21] WANG C, WEN C, LU Y. A fault diagnosis method by using extreme learning machine[C]// International Conference on Estimation, Detection and Information Fusion. IEEE, 2015: 318-322.

[22] LIU J, CHEN Y, LIU M,. SELM: Semi-supervised ELM with application in sparse calibrated location estimation[J]. Neurocomputing, 2011, 74(16): 2566-2572.

[23] IOSIFIDIS A, TEFAS A, PITAS I. Regularized extreme learning machine for multi-view semi-supervised action recognition[J]. Neurocomputing, 2014, 145(18): 250-262.

[24] HUANG G, SONG S, GUPTA J N,. Semi-supervised and unsupervised extreme learning machines[J]. IEEE Transactions on Cybernetics, 2014, 44(12): 2405-2417.

[25] ZHOU Y, LIU B, XIA S,. Semi-supervised extreme learning machine with manifold and pairwise constraints regularization[J]. Neurocomputing, 2015, 149(PA): 180-186.

[26] AVERDI B, MARQES I, GRANA M. Spatially regularized semisupervised ensembles of extreme learning machines for hyperspectral image segmentation[J]. Neurocomputing, 2015, 149: 373-386.

[27] ROWEIS S T, SAUAL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326.

[28] ZHAO H. Combining labeled and unlabeled data with graph embedding[J]. Neurocomputing, 2006, 69(16/17/18): 2385-2389.

[29] SINDHWANI V, NIYOGI P, BELKIN M. Beyond the point cloud: from transductive to semi-supervised learning[C]//ICML’05 Proceedings of the 22nd International Conference on Machine Learning Bonn, Germany, 2005: 824-831.

[30] MELACCI S, BELKIN M. Laplacian support vector machines trained in the primal[J]. Journal of Machine Learning Research, 2009, 12(5): 1149-1184.

[31] LEE J M, QIN S J, LEE I B. Fault detection of non-linear processes using kernel independent component analysis[J]. Canadian Journal of Chemical Engineering, 2008, 85(4): 526-536.

Reconstruction based semi-supervised ELM and its application in fault diagnosis

YI Weilin, TIAN Xuemin, ZHANG Hanyuan

(College of Information and Control Engineering, China University of Petroleum, Qingdao 266580, Shandong, China)

It is difficult to obtain labeled fault data while there are a multitude of unlabeled data available in industrial process, so how to utilize data information effectively is an important focal point in the field of fault diagnosis. A new semi-supervised learning method, reconstruction-based semi-supervised extreme learning machine (RSELM), was proposed for more sufficient data mining and information usage. Compared to traditional semi-supervised ELM, RSELM replaced random input weight in hidden layer with output weight, which was obtained by ELM auto-encoder (ELM-AE), such that data feature was extracterd more effectively. Since data could be reconstructed linearly by its neighbors, a self-adaptive reconstruction graph of neighboring data in combination with connection weight of optimal labeled data better reflected data structure information. A novel objective function preserving local structure information was further built to train classifier effectively. Simulation experiment on standard datasets and TE process demonstrated effectiveness of the proposed algorithm.

semi-supervised ELM; reconstruction;ELM-AE; fault diagnosis

10.11949/j.issn.0438-1157.20161252

TP 277

A

0438—1157（2017）06—2447—08

田学民。

易维淋（1991—），男，硕士研究生。

国家自然科学基金项目（61273160）。

2016-09-06收到初稿，2017-02-06收到修改稿。

2016-09-06.

Prof. TIAN Xuemin, tianxm@upc.edu.cn

supported by the National Natural Science Foundation of China (61273160).