空分短期停车时间阈值对氧气生产调度的影响

张培昆，王立,2



空分短期停车时间阈值对氧气生产调度的影响

张培昆1，王立1,2

（1北京科技大学能源与环境工程学院，北京 100083；2北京市高等学校节能与环保工程研究中心，北京 100083）

针对钢铁企业高炉休风场景下的氧气生产调度问题，提出以空分短期计划性停车为主要手段的调度策略，并基于MILP方法建立了氧气系统的优化调度模型。调度模型的优化目标为整个规划周期内氧气高压管网的综合压力最小化。模型包含了空分和部分氧气压缩机短期停车再启动操作的约束条件，并结合实际情况考虑了前述设备的停车时间阈值和运行时间阈值。以国内某大型钢铁企业为实际案例，验证了调度模型的合理性与可行性，然后基于模型计算分析了空分停车时间阈值对调度目标的影响规律。分析结果表明，减小空分停车时间阈值有利于获得更优的调度目标，但空分停车时间阈值对优化目标的影响规律具有阶跃特性，而非简单的比例关系。

钢铁冶金；分离；数学模型；氧气生产；优化；MILP

引 言

2015年中国粗钢产量超过8亿吨，占世界总产量的49.5%，钢铁行业节能降耗需求十分迫切。钢铁生产工艺所需氧气由低温精馏空气分离装置（以下简称“空分”或“ASU”）制取[1-2]，因此钢铁企业大都设有自备空分厂。空分制氧过程需要消耗大量电能，是钢铁企业中的耗电大户。除少量液体外卖，空分厂所生产的氧气只能供企业内部使用，因此保证氧气的供需平衡是维护生产安全及降低生产成本的重要环节。受转炉间歇吹炼和高炉休风等因素影响，钢铁企业经常出现氧气供需不平衡现象而产生放散损失。其中，转炉间歇吹炼造成的用氧波动因周期短、变化幅度小可通过空分调负荷和管网系统缓冲等手段消纳。而高炉休风造成的用氧波动持续时间长、变化幅度剧烈，其造成的用氧不平衡仅凭空分调负荷和管网系统缓冲难以消纳，而空分机组计划性短期停车成为平衡供需的重要手段。因涉及空分停开车操作，高炉休风期间的氧气生产调度十分复杂，其根本原因是系统内涵盖了空分机组、压缩机组、液化装置等数量众多功能及参数各异的设备。此外，同类设备的特性差异和操作人员经验不足等因素也增加了调度复杂性。因此，采用数学模型与计算机协助氧气调度十分必要。

生产调度问题是运筹学领域研究热点之一，但国内外文献针对钢铁企业氧气调度的报道相对较少。在国外，钢铁企业一般不设空分厂，所需氧气来源于气体公司的区域性供气系统。区域供氧管网覆盖半径较大，管网连接多个气体用户，因而用氧波动幅度较小。另外，长距离管网具有巨大的储气容量和缓冲能力，氧气波动通常可完全被管网消纳，供气系统一般不会产生氧气放散。因此，国外关于氧气生产调度的研究[3-18]主要针对气体公司，例如考虑市场电价波动对生产成本的影响以及液体产品的供应链管理等方面。在国内，近年来随着空分大型化，钢铁企业氧气供需不平衡问题日益突出，氧气生产调度研究日益受重视。国内钢铁企业自备空分厂不同于国外气体公司，例如用户数量和电价机制均不同。国外气体公司一般有多个用户，而自备空分厂通常只有其所属的钢铁企业这一个用户，国外气体公司用电来自电网，电力价格随用电时间和用电总量波动，而国内空分厂用电多来自钢铁企业内部发电厂，电力价格相对稳定。考虑到钢铁企业氧气调度问题的特殊背景，国内学者也为此展开了多方面探索。早年，刘姿等[19]、童莉葛等[20]基于线性规划方法建立了氧气决策支持系统，讨论了高炉休风等情况下的氧气放散率控制问题。陈光等[21]根据供需平衡原理，建立了氧气动态平衡模型和供氧决策模型，提出了氧气利用的决策方法及实施方案。莫友昆[22]提出了钢铁企业供氧决策系统的改进模型，并对区域性管网供气的决策支持系统做了初步探索。近年，杨见博[23]基于首钢京唐公司氧气系统，建立了氧气预测模型和优化分配模型，结果表明模型对氧气生产优化具有良好效果。陈聪等[24]针对氧气放散和管网压力波动问题，建立了混合整数非线性规划调度模型。吴佩林[25]以氧气生产、储存和使用单元模型为主要约束条件，建立了氧气放散量最小目标优化凸规划模型。Zhang等[26]针对钢铁企业大规模氧气系统，建立了以氧气放散量最小为目标的混合整数线性规划模型。

上述文献广泛探讨了氧气系统的优化问题，其中虽有少数报道涉及空分计划性短期停车调度，但未充分考虑空分停启特性对调度的影响。空分计划性短期停车是指连续运行中的空分因暂时不需要氧气而临时停车，但在近几个小时内因要求继续供氧而重新开车并恢复连续运行的短期操作，是降低氧气放散率的重要手段。空分短期停车操作的主要评价指标是空分从停车到再启动并输出纯度合格产品所需的最短时间，以下简称“短期停车时间阈值”。短期停车时间阈值越小，说明空分敏捷度越好及现场人员操作水平越高，但对于每台空分而言其短期停车时间阈值各不相同。此外，考虑到设备疲劳、启动损失、人员工作负荷等因素，调度还须纳入空分在线生产最短连续运行时间。众所周知短期停车时间阈值对氧气调度的灵活性具有重要影响，很多文献研究如何降低空分短期停车时间阈值，但时间阈值对调度的具体影响鲜有报道，影响规律仍不明晰。因此，本文针对国内某大型钢铁企业建立氧气调度数学模型，并以高炉休风用氧场景为研究案例，就空分短期停车时间阈值对氧气生产调度的影响展开分析，研究结果对钢铁企业氧气生产调度具有重要指导意义。

1 氧气系统供需平衡问题描述

图1为钢铁企业氧气供需关系示意图，氧气供需不平衡主因是供给侧和需求侧的设备运行规律不同。在供给侧，主要设备为空分。因设计原因，空分负荷只能在小范围内变化，且调负荷速率很有限[27]。若关停一台或几台空分，可以大幅度降低氧气产量，但因建立正常精馏工况的过程十分缓慢，空分重启后需等待较长时间（数小时）才能并网供气[28]。因此，氧气供给侧的调节能力有限且响应速度较慢。然而，用户侧氧气需求却变化频繁且速度较快。氧气用户主要为高炉炼铁和转炉炼钢，其中高炉炼铁利用常压氧气进行富氧鼓风，转炉炼钢则利用高压氧气吹炼铁水。氧气用量日常波动原因是转炉间歇式炼钢的随机性，其波动范围较小，供需不平衡可由高压管网缓冲消纳。而造成氧气用量剧烈波动的主要因素为高炉休风。高炉休风期间不再需要富氧鼓风，同时停止产出铁水，且后续转炉因缺乏铁水也进行停炉检修，氧气用量因而大幅下降。高炉复风后，氧气用量才逐渐恢复正常。高炉休风一般持续20 h左右，由于持续时间较长，期间一般采取空分计划性短期停车来调节氧气供需平衡。

调度建模关键环节是考虑空分短期停车再启动操作的时间特性。空分停车分长期停车和短期保冷停车，从停车状态重启到并网均需等待一段足够长的时间。本文主要考虑短期保冷停车，其再启动过程所需时间相对较短。空分短期停车的状态节点及时间特性如图2所示，主要有关停、停车、启动和在线运行。空分从在线运行状态切换至关停状态是瞬间完成的，但从关停开始后需经历一段足够长的时间（Tshut）空分才彻底停车。根据调度需要，停车持续时间（Tshut-down）可长可短，但应避免过短或过长。停车时间过短，空分启动损失所占比重过大，停车调度失去意义。停车时间过长，则不利于空分快速重启，据现场经验短期保冷停车一般不超过36 h。从关停切换到启动是瞬间完成的，但启动之后空分需要经历足够时长（Tstart）才能并网运行，该时间依赖于人员操作水平与设备响应特性等，文献报道有2～6 h不等。空分在线运行之后，为避免频繁停启一般会连续工作一段时间（Ton-line）。

2 数学模型

2.1 流程概况与建模假设

图3为国内某大型钢铁企业氧气系统流程，系统内配备5套大型空分，其中4套采用外压缩流程供常压氧气，另有一套采用内压缩流程供高压氧气。系统缓冲设备包括：高压氧气球罐，氧压机，液化装置及液体储罐。低压氧气除供炼铁厂等低压用户使用外，还可送入液化装置液化储存或经氧压机压送至高压管网供炼钢厂等高压用户使用。若氧气长期处于供大于求，高压管网压力会逐渐上升，管网压力上升会造成压缩机因排气压力增大而增加能耗，当高压管网压力达到上限后，还会造成氧气放散损失。建模过程采取的简化与假设如下：因高炉休风属于氧气过剩工况，调度对象限空分、压缩机、液化装置及气体球罐，而液体储罐及配套气化设施因主要用于氧气短缺工况而未纳入模型考虑范围。此外，忽略空分变负荷能力，主要出于以下两点考虑：首先，高炉休风期间氧气过剩，空分降负荷的减产作用可由空分停车代替，此举可避免空分在非设计负荷（低效率）情况下运行；其次，尽管空分自动变负荷技术已有应用，但实际上企业中的空分变负荷能力往往达不到预期水平，原因是调负荷还需考虑许多内外部因素，比如设备特性、现场人员操作经验、频繁调负荷对设备寿命及现场人员工作积极性的影响、产品气纯度稳定性等。以避免放散、降低压送能耗为出发点，模型的优化目标为整个调度周期（）内氧气高压管网综合压力最小化。

2.2 目标函数

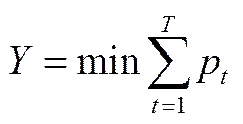
高压管网压力能够体现钢铁企业氧气系统的能效水平。作为缓冲系统重要环节，高压管网可以消纳氧气供需不平衡，代价是管网压力波动。高压管网系统储气容积十分有限，少量过剩氧气足以引发管网压力显著上升，从而导致所有压缩机工作在高排气压力状态下，压缩机耗能增大。换言之，过剩氧气给氧气压送能耗带来的影响不仅为过剩氧气本身，而是整个需要压送的氧气量（转炉用氧、高压氧液化等）。上述内容是模型目标函数[式（1）]设立的原因。

2.3 空分启动操作约束

因同一台空分在同一时刻只能下达一个指令，即关停或启动，故空分停启操作需通过式（2）、式（3）进行约束。

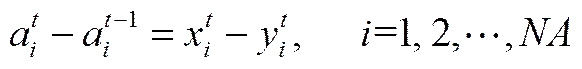
(3)

2.4 空分短期停车及运行时间阈值约束

空分启动后并不能立即并网供气，其停车后再启动所需时间具有最小临界值，即短期停车时间阈值，满足0≤-Tshut-Tstart≤Tshut-down。空分并网供气后，考虑到设备寿命等因素须持续运行一段时间，即运行时间阈值，满足≤Ton-line。由此，空分停启需由式（4）、式（5）进行约束。为简化调度，设高炉休风期间每台空分最多允许一次停车操作，为此将运行时间阈值设定为调度周期和短期停车时间阈值之差，如式（6）所示。

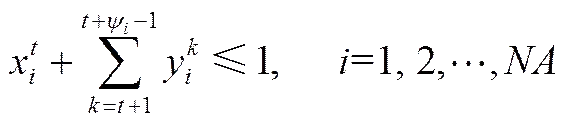
(5)

=-,=1,2,…,(6)

2.5 液化装置的运行约束

空分厂液化装置一般被设计成始终液化氮气。因液氮的沸点低于液氧，故液氧可通过氧气与液氮进行冷㶲置换获得。虽然液化装置在恒定负荷下连续运行[29]，但其液氧/液氮产出比例可调，即氧液化量可在最大值max和最小值min间任意变化，其约束条件如式（7）所示。

2.6 固定负荷压缩机的启动操作约束

压缩机分固定负荷和变负荷两种类型，其中固定负荷压缩机具有恒定的输气量且压缩机频繁停启。类似于空分，对同一台压缩机在同一时刻只能下达一个指令，即关停或启动，故压缩机停启需由式（8）、式（9）进行约束。

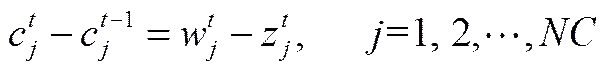
(9)

2.7 固定负荷压缩机停车及运行时间阈值约束

为避免压缩机停启过于频繁，调度中应设置压缩机的运行时间阈值CTon-line和停车时间阈值CToff-line，故压缩机停启需由式（10）、式（11）进行约束。

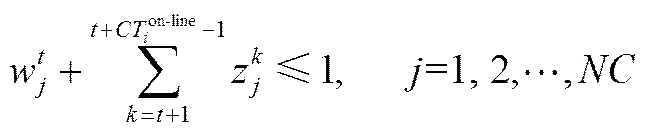
(11)

2.8 变负荷压缩机的运行约束

变负荷压缩机用于承担压缩任务中的基础负荷，除非需要进行检修维护，其一直处于运行状态。因变负荷范围及速率均有限度[30]，变负荷压缩机需受式（12）、式（13）约束。

(13)

2.9 氧气管网物料平衡约束

常压氧气管网属微正压运行，其储气能力及缓冲容量可忽略不计。常压氧气供给须始终满足高炉等用户用氧需求且不出现放散，其管网物料平衡关系如式（14）所示，即常压氧气总产量等于液化量、压缩量及常压氧需求量总和。而对于高压氧气管网，则可通过管网压力变化实现氧气储存与快速吞吐。高压管网系统物料平衡关系如式（15）所示，即高压氧气总产量、压缩量之和减去高压氧需求量、液化量之和等于高压管网储量。此外，根据安全限制和炼钢工艺要求，高压管网压力必须维持在特定范围之内，故模型约束条件还应包括式（16）。

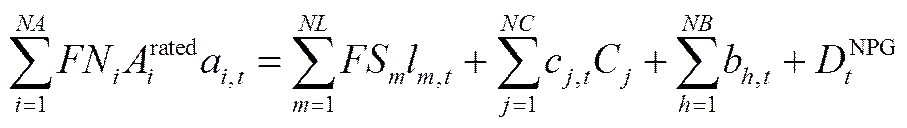
(15)

(16)

3 案例研究

本案例用于研究高炉休风期间的氧气调度。图4是一段时长48 h的各主要用户氧气用量趋势图（包含时长18 h的高炉休风）。如图4(a)所示，炼铁厂中的一座高炉从第8 h开始休风，在第26 h休风结束。休风期间，炼铁厂氧气需求量急剧下降。高炉休风还影响到后续的1#炼钢厂，如图4(b)所示，受铁水供应不足影响，1#炼钢厂用氧量骤减，休风结束后用氧量才逐渐恢复正常。表1～表4给出了案例中各单元设备的基本参数。首先，为验证模型的可行性与合理性，基于上述案例数据，本文以短期停车时间阈值=24 h为例进行优化分析，形成的调度模型共包含336个连续变量，1968个0-1变量和2881个约束条件。

模型采用美国LINDO公司开发的Lingo 16.0软件进行求解计算，Lingo 16.0是当前领先的数学规划求解商业软件，可快速高效求解线性规划与混合整数线性规划问题。将模型用Lingo建模语言描述并输入软件，软件自动通过其内嵌的MILP求解器进行求解计算，其具体算法为分枝定界法。基于Intel Core 2.4 GHz处理器，软件获得模型最优解所需的平均时间约为10 min。优化计算得到的空分、压缩机、液化装置等设备的调度结果展示在图5中。进而，在模型得到验证后，为分析空分短期停车时间阈值对调度的影响规律，本文还对短期停车时间阈值分别为6、9、12、15、18、21、27、31 h情况下的调度进行了优化计算，优化结果对比展示在图6～图12中。

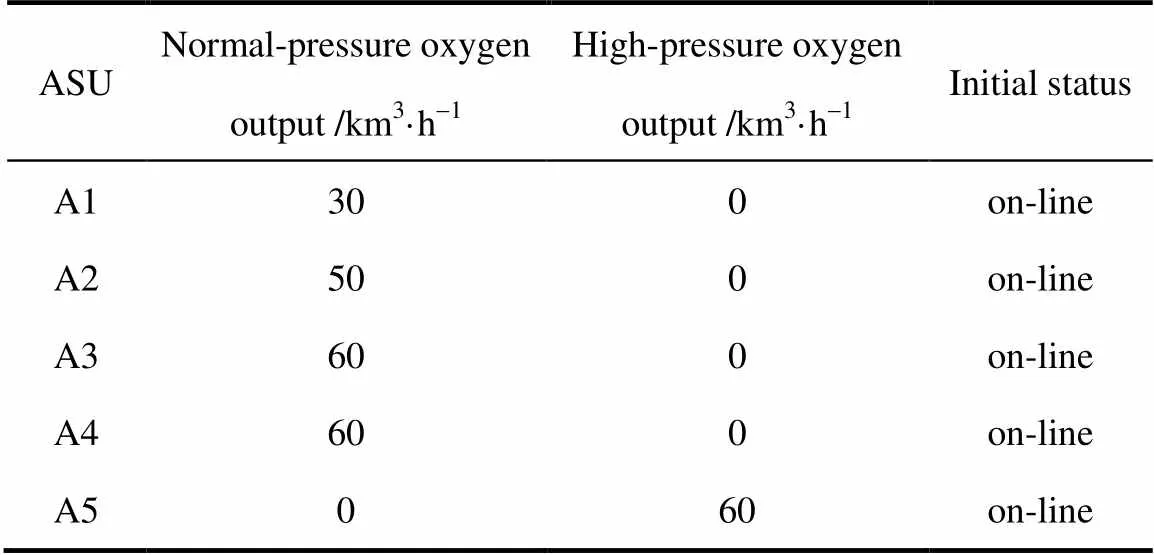
表1 空分参数

表2 液化装置参数

表3 压缩机参数

Note: C1 and C2 with variable load; C3—C6 with fixed load.

表4 高压气体储罐参数

图5给出了停车时间阈值τ=24 h情况下案例的优化结果。图5(a)表明模型可有效完成空分停开车配置，且空分停开车时间特性满足时间阈值的要求，说明优化结果可应用于实际调度，优化模型具有可行性。如图5(a)所示，针对图4所示氧气需求，整个规划周期内5台空分中有3台涉及停启操作。综合对比停开车甘特图发现，优化结果可按规划周期分3个部分进行分析，即第1～9周期、第10～29周期和第30～48周期。

第1～9周期，如图5(a)所示，空分A2在大部分时间中处于停车状态。该调度结果似乎有悖于正常推理，因为在高炉休风之前就关停空分可能会导致氧气供应短缺。然而，图5(f)所示管网压力却验证了调度结果的合理性，在空分A2停车后，高压管网压力随着时间推移而下降，说明优化模型试图清空高压管网的初始储量，并将高压管网压力降低至其下限，这与优化目标是一致的。如图5(e)所示，此时氧气总产量虽小于总需求，但通过释放管网初始储量，氧气供需平衡仍可保障。为配合上述操作，如图5(c)、(d)所示，模型安排压缩机C1和C2低负荷运行并且关停压缩机C3～C6，由此降低氧气压送量。因上述调度操作已充分平衡供需，两台液化装置在大部分时间内[图5(b)]保持低负荷运行。

第10～29周期，如图5(a)所示，模型同时关停空分A2和A3以应对高炉休风引起的氧气需求骤降。尽管如此，氧气总产量仍略高于总需求[图5(e)]，但由于此时供需不平衡较小，加之供需差异波动频繁，只能采取除空分停机之外的手段消纳过剩氧气。一般而言，有3种微调手段可供选择，即空分调负荷、高压管网缓冲、液化装置。本文模型主要依靠液化装置进行供需平衡微调，这与文献模型[24,26]不同，原因是本文优化目标要避免压力波动上升且空分负荷固定。虽然文献[24,26]中常采用空分调负荷消除供需差异，但具备保冷停机条件下，应尽量使空分在其设计负荷下高效率运行，因为负荷微小变化可通盘降低整台空分能效水平。相比之下，氧气液化带来的能耗仅限于液化装置其自身，并且该部分能耗可从氧气综合能耗中剥离，因为液化能耗最终将被转移到液体产品上并通过液体销售而得到回报。

第30～48周期，如图5(a)所示，空分A2开始生产运行，模型安排一台空分（A3或A4）始终保持停车状态，原因是此时高炉虽已复风，但高炉铁水产量和氧气需求仍然低于正常水平。图5(f)中的压力曲线在某些时段出现一些小峰值，原因是此时氧气产量略大于需求，这说明在某些时间点两台液化装置尽管已满负荷运行[图5(b)]，而氧气供需平衡仍需依赖管网缓冲。此时，为配合上述操作，如图5(c)、(d)所示，模型安排压缩机C1和C2高负荷运行并启动压缩机C3～C6，由此提高氧气压送量。

上述分析表明，图5(f)中高压管网压力是全局优化结果，同时可知各设备调度结果是模型为保证整个规划周期管网压力最小而做出的合理选择，由此阐明了本文优化模型的适用性及其调度结果的合理性。总体上，如图5(f)所示，氧气高压管网压力处以较低水平，节能效果显著。与文献模型[24,26]相比，本文模型的优势在于其有机结合了以下3个调度因素，即以管网压力最小化作为优化目标，以空分保冷停机作为供需平衡主要调节手段，以液化作为供需平衡的微调手段。

图6～图9给出了在不同空分停车时间阈值条件下各种设备的调度结果，其中，图6为空分的运行甘特图，图7为液化装置液化速率，图8为变负荷压缩机的输气量，图9为固定负荷压缩机的运行甘特图。图10和图11分别给出了在不同空分停车时间阈值条件下氧气总产量和高压管网压力的调度结果。以规划周期为视角，经图6可发现在所有停车时间阈值情况下，空分在高炉休风期间的停车密集程度最高，高炉休风后期次之，而在高炉休风前最低。该规律符合氧气供需不平衡程度在整个规划周期内的变化趋势，说明模型有效优化安排了5台空分的运行。由图6还可发现各台空分停车时间均大于其相应阈值，并且在规划周期内仅停车一次，说明所有情况下模型的时间阈值约束有效。在调度安排之下，氧气总产量和需求总量基本吻合（图10），供需细微差异通过液化装置和压缩机进一步消除，最终实现高压管网压力基本接近下限水平（图11），由此降低氧气压送能耗。上述结果表明，在各种时间阈值条件下，本文模型均能够合理有效的调度氧气生产与输配。

以空分停车时间阈值为视角观察图6、图10和图11可发现，从总体趋势来讲，空分停车时间阈值越小，涉及停车操作的空分数量越多，氧气总产量越接近总需求从而使得高压管网压力越低。换言之，时间阈值增大意味着空分调度灵活度降低，在同等条件下氧气高压管网压力会增大，这是图11中压力曲线起伏程度随时间阈值增大而逐渐增大的原因。总体而言，减小停车时间阈值有利于调度目标，但具体观察每个时间阈值对应的结果发现，时间阈值为15、18、21、24、27 h这5种情况下的空分运行甘特图及其高压管网压力曲线是相同的，即在此范围内空分停车时间阈值对调度结果没有影响。该影响规律可经图12得到进一步说明，图12中两条曲线分别给出了高压管网平均压力（由图11中的压力计算而得，代表了案例的优化目标）随停车时间阈值的变化关系，和涉及停车操作的空分数量（由图6计算而得）随停车时间阈值的变化关系。随着空分停车时间阈值增加，高压管网平均压力先是呈上升趋势（6、9、12 h），随后进入一个平台期（15、18、21、24、27 h），随后继续呈增大趋势（30 h）。可见，空分停车时间阈值对调度目标的影响规律具有阶跃特性，而非简单的比例关系。平台期的存在说明空分停车时间阈值只是空分停车调度的影响因素之一，调度中空分停车时间的长短还受实际场景中氧气供需不平衡程度等因素的影响。

此外，结合图6和图12可发现，尽管在低时间阈值条件下模型获得了更优的调度目标，但同时空分短时间停车情况增多，涉及停车操作的空分数量也相应增加。空分停车再启动过程会带来一定数量的未达标产品气放散损失，因此，进一步考虑空分停车次数的优化调度还有待后续研究。

4 结 论

（1）案例计算表明MILP模型能有效应用于包含空分及压缩机停开机操作的氧气生产调度。

（2）与空分调负荷的调度模型相比，包含空分停开车操作的调度模型不仅可避免氧气放散损失，还能有效降低高压氧气管网的压力，从而降低氧气压缩机的能耗。

（3）空分停车时间阈值对优化目标（高压氧气管网的压力）的影响规律具有阶跃特性（存在平台期），而非简单的比例关系。平台期的存在说明空分停车时间阈值只是空分停车调度的影响因素之一，调度中空分停车时间的长短还受实际场景中氧气供需不平衡程度等因素的影响。本结论对钢铁企业空分停车策略与氧气生产调度具有实际指导意义。

符 号 说 明

Airated ——空分额定氧产量，m3·h-1 ati——空分的运行状态 Bhmax——变负荷压缩机最大排气量，m3·h-1 Bhmin——变负荷压缩机最小排气量，m3·h-1 bh,t——变负荷压缩机的排气量，m3·h-1 Cj——固定负荷压缩机排气量，m3·h-1 CTioff-line ——固定负荷压缩机最小关停时间，h CTion-line ——固定负荷压缩机最小运行时间，h ctj——固定负荷压缩机的运行状态 DtHPG ——高压氧气需求量，m3·h-1 DtNPG——常压氧气需求量，m3·h-1 FNi——空分产品氧气压力水平 FSm——液化装置原料氧气压力水平 Lmmax——液化装置最大液化速率，m3·h-1 Lmmin——液化装置最小液化速率，m3·h-1 lm,t——液化装置的液化速率，m3·h-1 Pmax——高压氧气管网压力上限，Pa Pmin——高压氧气管网压力下限，Pa pt——高压氧气管网的压力，Pa R——气体常数，8.31446 m3·Pa·K−1·mol−1 T——规划周期，h Te——环境温度，K Dt——时间步长，h Vf——高压球罐的容积，m3 vh——变负荷压缩机变负荷速率，m3·h-2 wtj——固定负荷压缩机的启动状态 xti——空分的启动状态 yti——空分的停车状态 ztj——固定负荷压缩机的停车状态 ti——空分的最小关停时间，h yi——空分的最小运行时间，h 下角标 f——高压球罐编号(f =1, 2,…,NF) h——变负荷压缩机编号(h=1, 2,…,NB) i——空分编号(i=1, 2,…,NA) j——固定负荷压缩机编号(j=1, 2,…,NC) m——液化装置编号(m=1, 2,…,NL) t——时间周期(t =1,2,…,T)

References

[1] 李化治. 制氧技术[M]. 2版. 北京: 冶金工业出版社, 2009. LI H Z. Oxygen Technology[M]. 2nd ed. Beijing: Metallurgical Industry Press, 2009.

[2] FU Q, KANSHA Y, SONG C,. A cryogenic air separation process based on self-heat recuperation for oxy-combustion plants[J]. Appl. Energ., 2016, 162: 1114-1121.

[3] MANENTI F, ROVAGLIO M. Operational planning in the management of programmed maintenances—a MILP approach [C]//Proceedings of the 8th IFAC Symposium on Dynamics and Control of Process Systems, DYCOPS. 2007, 8: 279-284.

[4] GLANKWAMDEE W, LINDEROTH J, SHEN J,. Combining optimization and simulation for strategic and operational industrial gas production and distribution[J]. Comput. Chem. Eng., 2008, 32(11): 2536-2546.

[5] MITRA S, GROSSMANN I E, PINTO J M,. Optimal production planning under time-sensitive electricity prices for continuous power-intensive processes[J]. Comput. Chem. Eng., 2012, 38: 171-184.

[6] MANENTI F, BOZZANO G, D'ISANTO M,. Raising the decision‐making level to improve the enterprise‐wide production flexibility[J]. AIChE J., 2013, 59(5): 1588-1598.

[7] MANENTI F, ROVAGLIO M. Market-driven operational optimization of industrial gas supply chains[J]. Comput. Chem. Eng., 2013, 56: 128-141.

[8] MITRA S, PINTO J M, GROSSMANN I E. Optimal multi-scale capacity planning for power-intensive continuous processes under time-sensitive electricity prices and demand uncertainty(Ⅰ): Modelling[J]. Comput. Chem. Eng., 2014, 65: 89-101.

[9] MITRA S, PINTO J M, GROSSMANN I E. Optimal multi-scale capacity planning for power-intensive continuous processes under time-sensitive electricity prices and demand uncertainty(Ⅱ): Enhanced hybrid bi-level decomposition[J]. Comput. Chem. Eng., 2014, 65: 102-111.

[10] MARCHETTI P A, GUPTA V, GROSSMANN I E,. Simultaneous production and distribution of industrial gas supply-chains[J]. Comput. Chem. Eng., 2014, 69: 39-58.

[11] ROSSI F, MANENTI F, REKLAITIS G. A general modular framework for the integrated optimal management of an industrial gases supply-chain and its production systems[J]. Comput. Chem. Eng., 2015, 82: 84-104.

[12] KOPANOS G M, XENOS D P, CICCIOTTI M,. Optimization of a network of compressors in parallel: operational and maintenance planning–the air separation plant case[J]. Appl. Energ., 2015, 146: 453-470.

[13] ZHANG Q, GROSSMANN I E, HEUBERGER C F,. Air separation with cryogenic energy storage: optimal scheduling considering electric energy and reserve markets[J]. AIChE J., 2015, 61(5): 1547-1558.

[14] XENOS D P, NOOR I M, MATLOUBI M,. Demand-side management and optimal operation of industrial electricity consumers: an example of an energy-intensive chemical plant[J]. Appl. Energ., 2016, 182: 418-433.

[15] ZHANG Q, SUNDARAMOORTHY A, GROSSMANN I E,. A discrete-time scheduling model for continuous power-intensive process networks with various power contracts[J]. Comput. Chem. Eng., 2016, 84: 382-393.

[16] PATTISON R C, TOURETZKY C R, JOHANSSON T,. Optimal process operations in fast-changing electricity markets: framework for scheduling with low-order dynamic models and an air separation application[J]. Ind. Eng. Chem. Res., 2016, 55 (16): 4562-4584.

[17] PURANIK Y, KILINC M, SAHINIDIS N V,. Global optimization of an industrial gas network operation[J]. AIChE J., 2016, 62 (9): 3216-3224.

[18] CAO Y, SWARTZ C L E, FLORES-CERRILLO J. Optimal dynamic operation of a high-purity air separation plant under varying market conditions[J]. Ind. Eng. Chem. Res., 2016, 55 (37): 9956-9970.

[19] 刘姿, 汤学忠, 赵立合. 钢铁企业氧气合理利用支持系统的开发研究[J]. 冶金能源, 1998, 17(6): 6-11. LIU Z, TANG X Z, ZHAO L H. R&D on oxygen rational utilization system in iron and steel enterprises[J]. Energ. Metall. Ind., 1998, 17(6): 6-11.

[20] 董莉葛, 王立, 汤学忠, 等. 降低氧气放散率的高炉休风模型[J]. 冶金能源, 1999, 18(3): 16-19. TONG L G, WANG L, TANG X Z,. Model of blast furnace blow down for oxygen releasing rate[J]. Energ. Metall. Ind., 1999, 18(3): 16-19.

[21] 陈光, 陆钟武, 蔡九菊, 等. 钢铁企业氧气系统动态仿真[J]. 东北大学学报 (自然科学版), 2002, 23(10): 940-943. CHEN G, LU Z W, CAI J J,. Dynamic simulation of oxygen supply system in iron and steel company[J]. J. Northeastern University (Natural Science), 2002, 23(10): 940-943.

[22] 莫友坤. 钢铁企业供氧优化决策支持系统研究[D]. 武汉: 华中科技大学, 2004. MO Y K. Research about the decision support system of iron and steel enterprise optimum oxygen supply[D]. Wuhan: Huazhong University of Science & Technology, 2004.

[23] 杨见博. 钢铁企业氧气系统决策分析与优化模型研究[D]. 沈阳: 东北大学, 2012. YANG J B. A research on the decision analysis and optimization model of oxygen system of iron and steel enterprises[D]. Shenyang: Northeastern University, 2012.

[24] 陈聪, 赵均, 邵之江. 钢铁企业氧气管网的平衡与调度研究[J]. 计算机与应用化学, 2012, 29(9): 1089-1094. CHEN C, ZHAO J, SHAO Z J. Balance of the oxygen pipe network and scheduling in iron and steel enterprises[J]. Comput. Appl. Chem., 2012, 29(9): 1089-1094.

[25] 吴佩林. 钢铁企业氧气预测与优化调度模型研究[D]. 昆明: 昆明理工大学, 2013. WU P L. Study on the oxygen prediction and optimization scheduling of iron and steel enterprises[D]. Kunming: Kunming University of Science and Technology, 2013.

[26] ZHANG P, WANG L, TONG L. MILP-based optimization of oxygen distribution system in integrated steel mills[J]. Comput. Chem. Eng., 2016, 93: 175-184.

[27] XU Z, ZHAO J, CHEN X,. Automatic load change system of cryogenic air separation process[J]. Sep. Purif. Technol., 2011, 81(3): 451-465.

[28] MANENTI F, MANCA D. Transients modelling for enterprise-wide optimization: generalized framework and industrial case study[J]. Chem. Eng. Res. Des., 2009, 87(8): 1028-1036.

[29] ZHU Y, LEGG S, LAIRD C D. A multiperiod nonlinear programming approach for operation of air separation plants with variable power pricing[J]. AIChE J., 2011, 57(9): 2421-2430.

[30] LI Y, WANG X, DING Y. A cryogen-based peak-shaving technology: systematic approach and techno-economic analysis[J]. Int. J. Energ. Res., 2013, 37(6): 547-557.

Effects of temporary shutdown time-threshold on oxygen production schedule in air separation unit

ZHANG Peikun1, WANG Li1,2

(1School of Energy and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China;2Beijing Engineering Research Center for Energy Saving and Environmental Protection, Beijing 100083, China)

Aimed at oxygen scheduling challenge under the scenario of blast furnace blow-down in integrated iron steel enterprises, a control strategy based on short-term shutdown of air separation units (ASUs) was proposed with an establishment of optimal scheduling model for oxygen distribution system by the mixed integer linear program. The objective of model optimization was to minimize overall oxygen pressure across high pressure oxygen piping network during entire scheduled cycle. The model included constraints for temporary shutdown and restart of ASUs and some oxygen compressors, as well as stop and run time thresholds of theseequipment in real situations. A case study of a mega integrated iron and steel enterprise in China was performed to examine rationality and feasibility of the proposed model and to analyze effects of shutdown time threshold of ASUs on scheduling target by the model. The results show that a shorter shutdown time-threshold of ASU is generally propitious to achieve more optimal objective, which relationship between time-threshold and scheduling objective has non-linear leaping characteristic.

iron and steel making; separation; mathematical modeling; oxygen production; optimization; mixed integer linear program

10.11949/j.issn.0438-1157.20161690

TF 724.4

A

0438—1157（2017）06—2423—11

王立。

张培昆（1983—），男，博士，讲师。

国家自然科学基金项目（51306015）；高等学校博士学科点专项科研基金项目（20130006120015）。

2016-11-30收到初稿，2017-02-27收到修改稿。

2016-11-30.

Prof.WANG Li, liwang@me.ustb.edu.cn

supported by the National Natural Science Foundation of China (51306015) and the Specialized Research Fund for the Doctoral Program of Higher Education (20130006120015).