基于相似理论的月球车坡面通过性能试验

王 颖 黄 晗 李建桥 陈百超 邹 猛

(1.吉林大学工程仿生教育部重点实验室， 长春 130025； 2.中国空间技术研究院， 北京 100194)

基于相似理论的月球车坡面通过性能试验

王 颖1黄 晗1李建桥1陈百超2邹 猛1

(1.吉林大学工程仿生教育部重点实验室， 长春 130025； 2.中国空间技术研究院， 北京 100194)

基于相似理论开展月球车轮壤相互作用系统参数量纲分析，分别以模拟月壤内聚力和密度参数不变为约束条件，推导了轮壤系统参数比例尺。采用轻质量模型样车法当量月面低重力环境影响，设计1/2比例月球模型样车；以速度和坡度为试验因素，开展月球车坡面通过性试验；分析了试验因素对各车轮滑转率和沉陷量的影响规律；讨论了不同坡度条件下驱动扭矩、挂钩牵引力和牵引系数随滑转率的变化规律。结果表明，坡度对通过性的影响明显较速度的大；随着滑转率的增加，驱动扭矩和挂钩牵引力呈现增加趋势，最大值分别为3.6 N·m和10.5 N；牵引系数呈现先增加后减小趋势，在滑转率为21.6%时达到最大值0.18。为保障月球车安全可靠的通过性能，其巡视坡度在20°以内合理。

车辆; 车轮; 相似理论; 月球车; 坡面; 行驶特性

引言

随着各国深空探测任务的发展，无人探测车辆成为执行巡视勘测任务的主要工具。星球车在星球表面移动过程中，会遇到多种复杂类型地形地貌，包括坡地、沙丘和撞击坑等[1]。为确保在轨月球车探测任务顺利进行，充分的地面试验需发挥重要作用。为顺利开展地面验证试验，月球车行驶环境的模拟显得尤为重要，包括月球表面低重力环境、地形地貌、星壤的模拟等[2-4]。

低重力环境的模拟方法主要包括悬挂起吊重力补偿法、抛物线飞行法和构造轻质量模型样车法[5]，其中，悬吊重力补偿法的工程设备复杂、控制精度要求高，而抛物线飞行法存在成本较高、低重力持续时间短等问题[6]。轻质量模型样车法则是基于相似理论，通过一定比例缩小车辆结构参数，减小车体质量，来当量于低重力对行驶性能产生的影响[7-8]，具有简单、准确等优点。江磊等[9-11]基于地面力学理论，从轮壤相互作用模型出发，引入相似理论推导了轮壤交互作用无因次全组，建立了车轮-月壤交互系统的地面力学相似模型，以模拟月壤密度不变为约束条件，选取不同的线性比例尺，推导了相应模型试验比例因数，并提出一种全尺寸的牵引性能模型试验方法，为在地面开展模拟低重力环境下的月球车验证试验提供了一定的理论基础和技术方法。但该方法忽略了模拟月壤内聚力对试验的影响。

月球表面地貌主要分为月海、撞击坑等，其中，月海平原最大坡度约为17°，撞击坑外侧坡度平缓，一般小于25°[1]。针对以上地貌数据，为使月球车能够在月表大部分路面行走，要求月球车能够翻越25°的坡面，开展月球车坡面通过性能试验，对于确保任务可靠性具有重要意义。近些年来，国内外学者在这方面开展了研究。黄卫东等[12]针对月表坡面路况，分析了轮壤相互作用模型，建立月球车坡面行驶地面力学模型，进行坡面运动性能仿真分析，限于试验条件，未能对仿真结果进行全面验证。 IIZUKA等[13]在15°坡面，对不同轮型的单轮进行土槽试验，提出了一种基于滑转率和沉陷的挂钩牵引力模型，但该研究未在不同坡度水平下开展进一步分析。HIROAKI等[14]分析了偏航姿态的月球车坡面行驶时，车体平行水平面和坡面2种配置下车轮滑转沉陷规律，建立了关于车体质心高度和轮上载荷的轮壤关系力学模型，以及基于滑转率和侧向滑转角的轮壤接触力学模型，为在轨月球车路径规划、地面控制策略提供了重要理论依据。该研究未对俯仰姿态下的月球车坡面通过性模型进行研究。

本文基于相似理论，开展轮壤相互作用系统量纲分析，设计1/2比例月球模型样车；以车轮沉陷量、驱动扭矩、挂钩牵引力和牵引系数为指标，开展模型车俯仰姿态下坡面通过性试验，分析行驶速度和坡度对通过性的影响规律；分析不同坡度条件下驱动扭矩、挂钩牵引力和牵引系数随滑转率的变化规律。

1 量纲分析

出于经济和技术上的限制，工程上很多原型或实体试验无法在正常条件下进行，只能通过模型试验做出预测。模型试验研究中，模型的研制、试验方案的设计以及将模型试验的结果折算到原型上等问题则需要依靠相似理论来解决。相似理论是指2个系统中同一类物理现象全部物理量(如力、速度、时间等)成一定的比例，其中力学现象相似的3个条件是：几何相似、运动相似和动力相似。因此，为获取模型试验中模型参数与原型参数的比例，需对系统中各物理参数进行量纲分析。

基于上述相似理论原理，本文采用质量系统的质量、几何尺寸和时间3个基本物理量作为分析基础，对应的基本量纲分别用M、L和T表示。轮壤相互作用系统参数主要分为2类：

(1)土壤物理力学性能参数：内聚力c、内摩擦角φ、密度ρ、变形指数n、内聚模量kc和内摩擦模量kφ。其中，n为无量纲参数，而kc和kφ可引入Reece修正公式转换为无量纲的k′c和k′φ，故进行量纲分析时只考虑土壤的内聚力c和密度ρ[15-16]。

(2)车轮行驶参数：车轮滑转率s、沉陷量z、行驶速度v、挂钩牵引力FDP、驱动扭矩M和重力加速度g。其中，s为无量纲参数，z量纲则与基本量纲L相同，因此，在进行量纲分析时不考虑滑转率s和沉陷量z。

通过以上分析，本文将从轮壤相互作用系统的9个主要参量(表1)出发，进行量纲分析。

表1 轮壤相互作用系统主要参量及其量纲

根据泊金汉π定理和量纲齐次性原理，可推导出模型试验相似比例尺Kj为

Kj=je/jp

式中j为轮壤相互作用系统参量(表1)，下标“e”和“p”分别表示模型和原型参数。通过量纲分析得到轮壤相互作用系统主要参量的表达式为

(1)

式中Kg——地球表面重力加速度与月球表面重力加速度之比，针对月面环境Kg=6

由于试验中土壤介质参数的调节较为复杂且难以控制，因此，在推导轮壤相互作用系统各参数相似比例尺时，可基于土壤内聚力不变(Kc=1)和密度不变(Kρ=1)2种情况考虑。

当Kc=1时

(2)

当Kρ=1时

(3)

考虑到原型的总体尺寸以及模型加工制作的可行性，模型车与原型样车比例尺采用1/2(Kl=1/2)。由式(2)和式(3)可得Km分别为1/24(Kc=1)和1/8(Kρ=1)，对于前者模型车整体质量的控制较为困难，故本文采用后者Kl=1/2和Kρ=1为约束条件，得到其他参数相似比例如表2所示。

表2 模型试验相似比例

2 月球车坡面通过性试验

2.1 车轮-坡面相互作用计算模型

月球车在坡面行驶时，轮壤相互作用示意图如图1所示。车轮松软地面通过性评价指标包括驱动扭矩、挂钩牵引力和牵引系数等，沉陷量则是影响车辆通过性能的关键因素之一，车轮沉陷量计算模型是建立轮壤关系力学模型的基础[17-19]，基于Bekker理论的坡面车轮静态沉陷模型可表示为

(4)

式中i——车轮编号，i为1、2和3时依次表示月球车前轮、中间轮和后轮

zi——单轮沉陷量，m

Wi——单轮轮上载荷，N

β——坡度，rad

b——车轮宽度，m

D——车轮直径，m

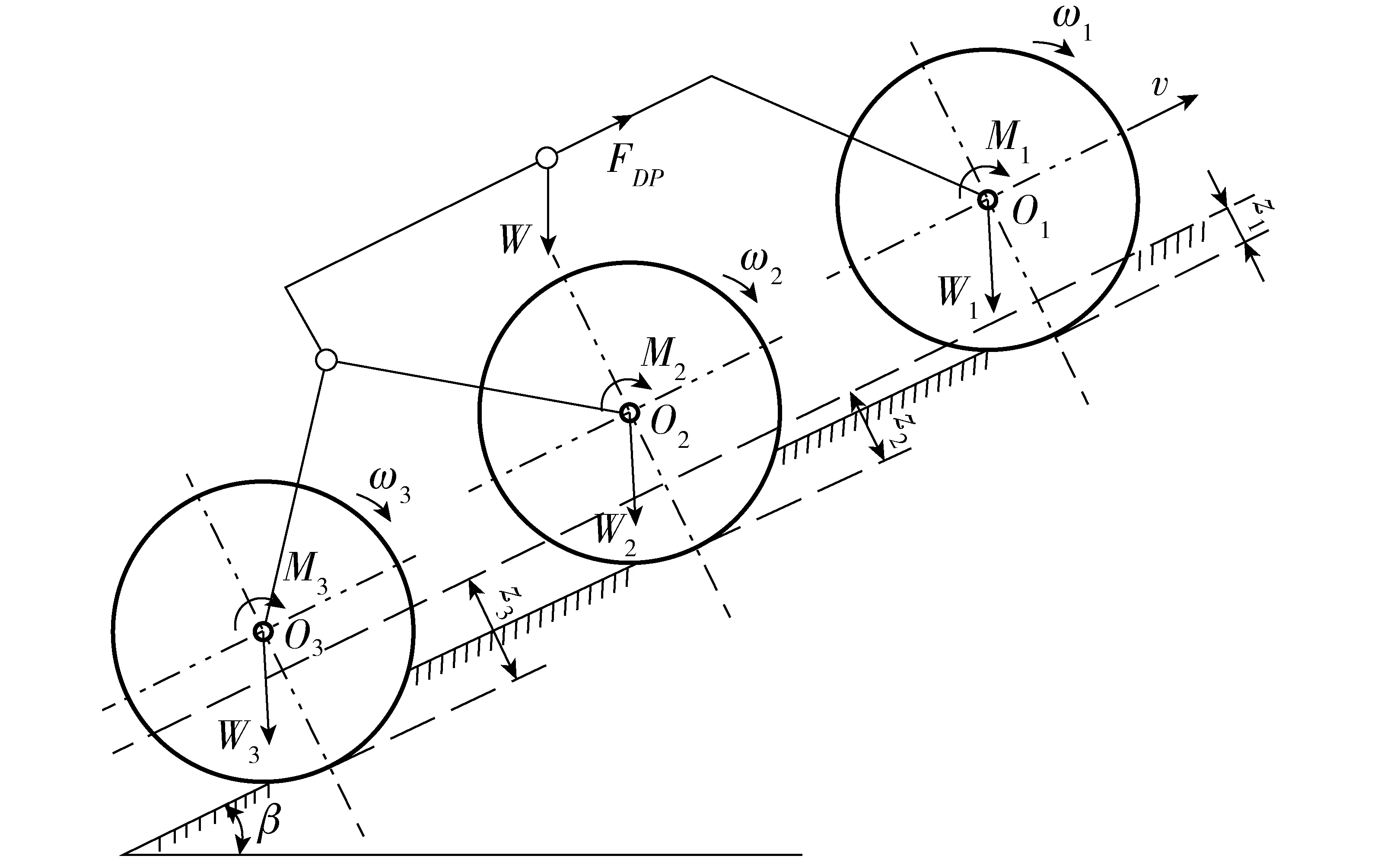
图1 月球车坡面行驶轮壤相互作用Fig.1 Wheel-soil interaction of lunar rover on slope terrain

月球车在坡面行驶过程中，重力沿坡面分力产生附加的挂钩牵引力，使得车轮出现打滑以及产生滑转沉陷，从而影响车辆整体的通过性能，因此，滑转率可作为通过性评价的另一重要评价指标，其表达式为

(5)

式中r——车轮半径，mv——车轮水平速度，m/sω——车轮角速度，rad/s

基于月球车的准静力平衡关系(图1)可得

Fni=Wicosβ

(6)

FDPi=Wisinβ

(7)

(8)

式中Fni——轮上法向载荷(轮上载荷Wi沿垂直坡面方向分力)，N

FDPi——单轮挂钩牵引力，N

基于WONG理论[18]可得

(9)

(10)

式中Mi——驱动扭矩，N·mTEi——效率系数θ——轮壤接触面上任意角度，radθ1i——车轮接近角，radθ2i——车轮离去角，radτi(θ)——轮下切向应力，Pa

2.2 试验条件

基于前文量纲分析，设计了1/2比例模型样车，如图2所示。模型车总体尺寸长、宽和高分别为750、500、220 mm。

图2 比例模型车Fig.2 Scaling model rover1.控制器 2.主摇臂 3.副摇臂 4.电源 5.驱动电动机6.差动机构 7.车轮

模型车采用摇臂悬吊式悬架，其中，控制器主要由无线控制单元组成，控制车轮转速和转向；为了减轻整车质量，主摇臂和副摇臂采用铝合金镂空结构；电源为蓄电池组，输出电压为12 V；驱动电动机为步进电动机，最大输出转速和转矩分别为26 r/min和1.5 N·m；车体中部安装有差动机构，以确保模型车在行驶过程中质心不会出现较大波动；车轮为筛网轮，采用ABS树脂材料3D打印加工成型，具有质量轻的优点，轮宽和轮径分别为75 mm和150 mm，轮面交替均匀分布有20个轮刺，宽度和高度分别为1 mm和5 mm。

图3 不同坡度和速度条件下滑转率变化规律Fig.3 Variation curves of slip ratio versus slope and velocity

试验介质为吉林大学工程仿生教育部重点实验室研制的JLU-2型模拟月壤，其原材料为火山灰，通过研磨、筛分和配制等工序加工而成[20-21]。试验前对模拟月壤进行翻松、坡面整备、刮平和坡度检测操作[22]，通过SC-900型土壤硬度计检测整备效果，贯入深度为150 mm，坡面模拟月壤圆锥贯入阻力随深度变化的梯度为1.89 kPa/mm，波动误差在10%以内，从而确保了试验的重复一致性。

2.3 试验方案

试验因素为坡面坡度和模型车前进速度，试验指标为车轮沉陷量和滑转率。试验中，车轮沉陷量和滑转率通过激光非接触测量装置获取[23-24]。

(1)月海、高地和撞击坑外侧地区大部分坡度在0°～23°之间。在使得月球车安全行驶前提下，能有较大范围内完成巡视勘查的科学探测，因此，本文最大坡度选择为25°，分等间距的5水平，间隔为5°。

表3 试验因素水平

3 结果分析

3.1 滑转率

图3为月球车各车轮滑转率随速度和坡度的变化规律，其中，前轮和中间轮的滑转率随试验因素变化趋势总体趋于一致，滑转率最大值均达到80%，而后轮仅为60%左右。

由图3可知，各车轮滑转率随着坡度增加而增加。随着坡度等水平依次增加，滑转率平均增加率分别为99.9%(前轮)、111.2%(中间轮)和79.6%(后轮)。坡度从15°增至20°时，前轮和中间轮滑转率变化最为明显，相对增加率分别达到225.8%和250.1%，分析是由于轮上法向载荷急剧减小所导致。当坡度β大于20°时，由于经过前轮和中间轮两次挖掘和压实作用使得模拟月壤密实度明显增加，后轮滑转率均较前轮和中间轮的小。

当坡度β小于15°时，滑转率随速度增加而减小，平均减小率分别为13.8%(前轮)、17.2%(中间轮)和18.1%(后轮)；当坡度β为20°时，滑转率随着速度增加先减小后增加，当坡度β为25°时，随着速度的增加，滑转率呈现增加趋势，最大增加率为10.2%。出现上述规律，分析是由于坡度较小时，速度对滑转率影响较坡度的大，当坡度超过20°后，坡度对滑转率的影响逐渐超过速度因素的影响。

以上分析可知，滑转率随坡度的增加而增加，随速度增加而减小，且前者对滑转率的影响明显较后者的大。随着坡度的增加，车轮挂钩牵引力增加、轮上法向载荷减小，当坡度超过20°后月球车滑转率急剧增加，通过性变差。

3.2 沉陷量

图4为不同坡度和速度条件下沉陷量的变化规律。随着坡度增加，各车轮沉陷量总体呈增加趋势，不同坡度区间的沉陷量变化率如表4所示，增加率平均值分别为43.8%(前轮)、47.1%(中间轮)和27.6%(后轮)。

图4 不同坡度和速度条件下沉陷量的变化规律Fig.4 Variation curves of sinkage versus slope and velocity

%

由图4a、4b可知，月球车前轮和中间轮沉陷量均随坡度增加而增加，且二者变化趋势基本保持一致，最大值分别为33.1 mm和33.9 mm。由图4c可知，后轮沉陷量随着坡度增加总体呈现增加趋势，但在坡度区间为15°～20°时，沉陷量随坡度增加而减小，分析是由于前轮和中间轮的掘土作用使得后轮前方模拟月壤基准面上升所导致。当坡度达到25°后，车轮挂钩牵引力增加，轮上法向载荷减小，导致滑转率急剧增加，车轮大部分能量消耗于挖掘土壤，导致沉陷量增大，且车轮后方土壤逐渐堆积产生壅土现象(图5)，车轮通过性变差。

图5 25°坡条件下车轮壅土现象Fig.5 Soil hilling phenomenon under 25° slope condition

随着速度的增加，沉陷量相对变化率范围为-12.5%～10.7%，因此速度对沉陷量的影响明显较坡度的小。沉陷量随速度增加所呈现出的规律与坡度相关：当坡度小于15°时，沉陷量随速度增加而减小；当坡度为20°时，沉陷量随着速度增加先减小后增加；当坡度为25°时，沉陷量随速度增加而增加。上述变化规律，分析可能是由于当坡度较小时，速度越大，轮壤接触时间减少，土壤未得到充分变形，使得车轮沉陷量减小；当坡度达到20°时，速度越大，对模拟月壤的冲击扰动越大，甚至出现滑坡现象，沉陷量相应增加。

综上所述，相同试验条件下，月球车前轮、中间轮和后轮的滑转率和沉陷量依次减小。各车轮滑转率均随坡度的增加而增加，随速度的增加则总体呈现先减小后增加趋势，且坡度的影响明显较速度的大。

3.3 通过性能

图6 月球车牵引通过性能Fig.6 Lunar rover’s traction trafficability

月球车牵引通过性能指标包括驱动扭矩、挂钩牵引力和牵引系数，如图6所示，月球车驱动扭矩和挂钩牵引力最大值分别为3.6 N·m和10.5 N。由图6a可知，驱动扭矩随滑转率增加总体呈现增加趋势，在滑转率约25%～60%范围内增加较为缓慢，平均增加率为2.2%；当滑转率超过60%以后，驱动扭矩增加明显，分析是由于较大的车轮沉陷量是使得壅土现象逐渐明显，月球车行驶阻力增大，导致驱动扭矩急剧增加。由图6b可知，挂钩牵引力随滑转率增加而增加。当滑转率达30%时，其增加率为230.6%；当滑转率超过40%以后，挂钩牵引力随滑转率的增加逐渐平缓，增加率约为18.4%。

由图6c可知，牵引系数随着滑转率的增加呈现先增加后减小趋势，其最大值为0.18，对应滑转率为21.6%。当牵引系数达到最大值后，牵引系数随滑转率增加而急剧减小；当滑转率达到60%时，牵引系数低于0.08，此时大多数的能量消耗于车轮的刨土，月球车巡视坡度在20°以内较为合理。

综上所述，坡度为20°时，前轮和中间轮的滑转率达到65%，坡面模拟月壤在车轮扰动下出现壅土现象，此时月球车的通过性较差，月球车可能进入危险工况；当坡度达25°时，前轮和中间轮沉陷量约为30 mm，滑转率接近90%，牵引系数低于0.1，此时月球车绝大部分能量消耗于车轮刨土，达到极限工况。考虑到能量消耗以及安全的通过性能，月球车巡视坡度在20°以内较为合理。

4 结论

(1)基于相似理论的量纲分析，分别以土壤内聚力和密度不变为约束条件，推导了轮壤系统参数比例尺计算公式，基于此设计了1/2比例月球模型样车。

(2)沉陷量随着坡度的增加总体呈现增加趋势，平均增加率分别为43.8%(前轮)、47.1%(中间轮)和27.6%(后轮)。沉陷量随着速度的增加总体呈现先减少后增加趋势，相对变化率范围为-12.5%～10.7%。

(3)驱动扭矩和挂钩牵引力随着滑转率增加总体呈现增加趋势，最大值分别为3.6 N·m和10.5 N；牵引系数在滑转率为21.6%时达到最大值0.18，当滑转率达到60%时，牵引系数低于0.08，此时月球车大多数的能量消耗于车轮的刨土，坡面通过性较差。

(4)当滑转率超过约65%时，月球车轮沉陷量和滑转率出现进一步增加趋势，进入危险工况。因此，考虑到能量消耗以及安全的通过性能，月球车巡视坡度在20°以内较为合理。

1 欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005.

2 邓宗全, 范雪兵, 高海波, 等. 载人月球车移动系统综述及关键技术分析[J/OL]. 宇航学报, 2012, 33(6): 675-689. http:∥www.yhxb.org.cn/CN/10.3873/j.issn.1000-1328.2012.06.001.DOI: 10.3873/j.issn.1000-1328.2012.06.001. DENG Zongquan, FANG Xuebing, GAO Haibo, et al. Review and key techniques for locomotive system of manned lunar rovers[J/OL]. Journal of Astronautics, 2012, 33(6): 675-689. (in Chinese)

3 程志红, 魏毅龙, 牛辉, 等. 行星探测车连杆式差动平衡机构设计及运动学分析[J/OL]. 宇航学报, 2015, 36(5): 524-532.http:∥www.yhxb.org.cn/CN/10.3873/j.issn.1000%EE%80%911328.2015.05.006.DOI:10.3873/j.issn.1000-1328.2015.05.006. CHENG Zhihong, WEI Yilong, NIU Hui, et al. Design and kinematic analysis of differential-balance mechanism for planetary exploration rover[J/OL]. Journal of Astronautics, 2015, 36(5): 524-532. (in Chinese)

4 贾阳, 申振荣, 庞彧, 等. 月面巡视探测器地面试验方法与技术综述[J/OL]. 航天器环境工程, 2014, 31(5): 464-469. http:∥www.bisee.ac.cn/ch/reader/view_abstract.aspx?file_no=20140502&flag=1.DOI:10.3969/j.issn.1673-1379.2014.05.002. JIA Yang, SHEN Zhenrong, PANG Yu, et al. A review of field test methods and technologies for lunar rover[J/OL]. Spacecraft Environment Engineering, 2014, 31(5): 464-469. (in Chinese)

5 刘振, 高海波, 邓宗全, 等. 摇臂转向架式星球车单索重力补偿[J/OL]. 机械工程学报, 2013, 49(7): 113-124. http:∥www.cjmenet.com.cn/Jwk_jxgcxb/CN/abstract/abstract6049.shtml.DOI: 10.3901/JME.2013.07.113. LIU Zhen, GAO Haibo, DENG Zongquan, et al. Gravity compensation for rocker-bogie rovers through single string tension[J/OL]. Journal of Mechanical Engineering, 2013, 49(7): 113-124. (in Chinese)

6 徐文福, 梁斌, 李成, 等. 空间机器人微重力模拟实验系统研究综述[J]. 机器人, 2009, 31(1): 88-96. XU Wenfu, LIANG Bin, LI Cheng, et al. A review on simulated micro-gravity experiment systems of space robot[J]. Robot, 2009, 31(1): 88-96. (in Chinese)

7 KURODA Y, TESHIMA T, SATO Y, et al. Mobility performance evaluation of planetary rover with similarity model experiment[C]∥IEEE International Conference on Robotics and Automation, 2004: 2098-2103.

8 WONG J Y. Predicting the performances of rigid rover wheels on extraterrestrial surfaces based on test results obtained on earth[J]. Journal of Terramechanics, 2012, 49(1): 49-61.

9 江磊, 郭建娟, 陈传海. 基于相似理论的月球车牵引性能模型试验[J]. 中国机械工程, 2009, 23(20): 2828-2831. JIANG Lei, GUO Jianjuan, CHEN Chuanhai. Scaling model experiment of lunar rover’s mobility performance based on similarity model theory[J]. China Mechanical Engineering, 2009, 23(20): 2828-2831. (in Chinese)

10 江磊, 郭建娟. 基于Vortex的月球车仿真技术[J/OL]. 农业机械学报, 2012,43(增刊): 352-356. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=2012s72&flag=1.DOI:10.6041/j.issn.1000-1298.2012.S0.072. JIANG Lei, GUO Jianjuan. Simulation algorithm of lunar rover based on Vortex [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012,43(Supp.): 352-356. (in Chinese)

11 李萌, 高峰, 孙鹏, 等. 基于相似理论的月球车月面牵引性能预测[J]. 北京航空航天大学学报, 2013, 39(2): 230-234. LI Meng, GAO Feng, SUN Peng, et al. Prediction of lunar rover’s moon tractive performance based on similitude theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 230-234. (in Chinese)

12 黄卫东, 鲍劲松, 徐有生, 等. 月球车坡路行驶地面力学模型与运动性能分析[J]. 机械工程学报, 2013, 49(5): 17-23. HUANG Weidong, BAO Jinsong, XU Yousheng, et al. Terramechanics model and movement performance analysis of a lunar rover for slope travel[J]. Journal of Mechanical Engineering, 2013, 49(5): 17-23. (in Chinese)

13 IIZUKA K, SATO Y, KUROD Y, et al. Experimental study of wheeled forms for lunar rover on slope terrain[C]∥9th IEEE International Workshop on Advanced Motion Control, 2006: 266-271.

14 HIROAKI I, MASATAKU S, KENJI N, et al. Modeling, analysis, and control of an actively reconfigurable planetary rover for traversing slopes covered with loose soil[J]. Journal of Field Robotics, 2013, 30(6):875-896.

15 REECE A R. Problems of soil vehicle mechanics[R]. Warren, Michigan: US Army Tank-Automotive Center, 1964.

16 MIKHAIL M , LRINA P, SERGEI F, et al. Locomotion concepts analysis for moon exploration [R]. St Petersburg: ESA, 1994.

17 TAHERI S, SANDU C, TAHERI S, et al. A technical survey on terramechanics models for tire-terrain interaction used in modeling and simulation of wheeled vehicles[J]. Journal of Terramechanics, 2015, 57(1): 1-22.

18 WONG J Y. Terramechanics and off-road vehicle engineering[M]. 2nd ed. Oxford: Elsevier, 2010.

19 丁亮亮, 肖杰, 宗魏, 等. 与沉陷相关联的星球车挂钩牵引力模型研究[J/OL]. 农业机械学报, 2014,45(12):37-42. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20141206&flag=1.DOI:106041/j.issn.1000-1298.2014.12.006. DING Liangliang , XIAO Jie, ZONG Wei, et al. Drawbar pull model of planetary rover associated with subsidence[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12): 37-42. (in Chinese)

20 ZOU Meng, FAN Shichao, SHI Ruiyang, et al. Effect of gravity on the mechanical properties of lunar regolith tested using a low gravity simulation device[J]. Journal of Terramechanics, 2015, 60(4): 11-22.

21 李建桥, 黄晗, 王颖, 等. 松软地面机器系统研究进展[J/OL]. 农业机械学报, 2015, 46(5):306-320. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150544&flag=1.DOI:10.6041/j.issn.1000-1298.2015.05.044. LI Jianqiao, HUANG Han, WANG Ying, et al. Development on research of soft-terrain machine systems[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5):306-320. (in Chinese)

22 李因武, 李建桥, 邹猛, 等. 月壤力学性质对月球车牵引性能影响的模拟[J]. 农业机械学报, 2009, 40(1): 1-4. LI Yinwu, LI Jianqiao, ZOU Meng, et al. Simulation of traction ability of lunar rover with different mechanics of lunar soil[J].Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(1): 1-4. (in Chinese)

23 王洋, 李建桥, 党兆龙, 等. 松散地面上车辙表面的非接触式激光测量[J/OL]. 农业机械学报, 2013, 44(7): 264-268. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130745&flag=1.DOI:10.6041/j.issn.1000-1298.2013.07.045. WANG Yang, LI Jianqiao, DANG Zhaolong, et al. Non-contact laser measurement of rutting surface on loose ground[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(7):264-268. (in Chinese)

24 黄晗, 李建桥, 党兆龙, 等. 基于相似理论的星球车牵引通过性模型[J/OL]. 航空学报, 2016, 37(6): 1974-1982. http:∥hkxb.buaa.edu.cn∥CN/10.7527/S1000-6893.2015.0217.DOI:10.7527/S1000-6893.2015.0217. HUANG Han, LI Jianqiao, DANG Zhaolong, et al. Study on planetary rover’s tractive performance model based on similarity theory [J/OL].Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1974-1982. (in Chinese)

25 GAO H B, GUO J L, DING L, et al. Longitudinal skid model for wheels of planetary exploration rovers based on terramechanics[J]. Journal of Terramechanics, 2013, 50(5): 327-343.

26 DING L, GAO H B, DENG Z Q, et al. New perspective on characterizing pressure-sinkage relationship of terrains for estimating interaction mechanics[J]. Journal of Terramechanics, 2014, 52(2): 57-76.

Experiment on Lunar Rover’s Trafficability on Slope Terrain Based on Similarity Theory

WANG Ying1HUANG Han1LI Jianqiao1CHEN Baichao2ZOU Meng1

(1.KeyLaboratoryofBionicEngineering,MinistryofEducation,JilinUniversity,Changchun130025,China2.ChinaAcademyofSpaceTechnology,Beijing100194,China)

Dimensional analysis on parameters of wheel-soil interaction system was performed, and the parameters’ scales were also acquired when the density and cohesion of simulant regolith were kept consistent, respectively. The lightweight model method was adopted to eliminate the influence of low gravity environment, and a 1/2 scale lunar rover model was designed. The slope angle and wheel velocity were taken as the experimental factors, the wheel sinkage and slip ratio were taken as the experimental index, test on lunar rover’s slope trafficability was carried out, and the experimental factors’ influences on the wheel sinkage and slip ratio were analyzed. Variation laws of the driving torque, drawbar pull and traction coefficient with the slip ratio under different slope conditions were analyzed. Results indicated that the influence of slope angle on trafficability was more obvious than that of wheel velocity. With the increase of slip ratio, the driving torque and drawbar pull presented increasing trend, and the maximum values of the driving torque and drawbar pull were up to 3.6 N·m and 10.5 N, respectively. The traction coefficient was increased first and then decreased with the increase of slip ratio, and it was up to its maximum value of 0.18 when the slip ratio was 21.6%. In order to ensure that the lunar rover had safe and reliable trafficability, the exploring slope angle within 20° was reasonable. The research result would provide a reference for the evaluation of lunar rover’s slope trafficability under low gravity environment.

vehicles; wheels; similarity theory; lunar rover; slope terrain; trafficability

10.6041/j.issn.1000-1298.2017.04.054

2016-07-29

2016-10-04

国家自然科学基金项目(51375199)

王颖(1982—)，女，博士生，主要从事地面机械仿生技术研究，E-mail： wang_ying13@mails.jlu.edu.cn

李建桥(1953—)，男，教授，博士生导师，主要从事地面机器系统及其仿生研究，E-mail： jqli@jlu.edu.cn

V474.3

A

1000-1298(2017)04-0406-07