Deform-X柔性铰链设计与分析
2017-06-05邱丽芳印思琪杨德斌
邱丽芳 王 栋 印思琪 杨德斌
(北京科技大学机械工程学院, 北京 100083)
Deform-X柔性铰链设计与分析
邱丽芳 王 栋 印思琪 杨德斌
(北京科技大学机械工程学院, 北京 100083)
设计了一种Deform-X柔性铰链,利用微积分的思想分析了其等效刚度,推导了Deform-X柔性铰链弯扭耦合等效刚度的理论计算公式。通过一组实例的理论分析和ABAQUS仿真分析,验证了Deform-X柔性铰链等效刚度理论计算公式的正确性。选取外形尺寸相同的X型柔性铰链与Deform-X柔性铰链进行了性能比较分析,在相同转矩作用下,Deform-X柔性铰链弯曲变形转角约为X型柔性铰链的3倍。分别对X型柔性铰链和Deform-X柔性铰链进行了弯曲失效分析,结果表明Deform-X柔性铰链的可使用范围大于X型柔性铰链。设计了基于Deform-X柔性铰链的平面折展四杆机构的实物模型,通过实物测试和仿真分析表明Deform-X柔性铰链能够实现预期变形。最后,对尺寸相同的基于X型柔性铰链的四杆机构和基于Deform-X柔性铰链的四杆机构在相同力矩作用下的变形进行了分析,结果表明基于Deform-X柔性铰链的四杆机构变形更大。
柔性铰链; 弯扭耦合; 等效刚度; 失效分析; 四杆机构
引言
柔性机构是通过柔性构件的弹性变形来输出力或运动的机构[1]。柔性机构的应用领域十分广泛[2-6],尽管柔性机构具有很多优势,但其变形运动范围经常受到限制,而且相比刚性机构,设计难度更大[7-8]。
平面折展机构(Lamina emergent mechanisms, LEMs)最大的优势是机构由二维薄板平面加工生成而能实现三维运动[9],可以实现如四杆机构、滑块机构[10-11]等简单的运动,还能实现如球面四杆机构、斯蒂芬森机构[12]等复杂的运动。同时,LEMs集合了正交机构、变胞机构和柔性机构的特性。LEMs实现特性和发挥优势的关键在于柔性铰链,几何尺寸、边界条件、材料特性等是影响其功能特性的关键因素[13]。JACOBSEN等[14]提出了关于LET柔性铰链等效刚度的理论计算公式;MAGLEBY等[15]设计了2种柔性铰链——RUFF柔性铰链和TUFF柔性铰链;DELIMONT等[16]总结概括了部分柔性铰链等效刚度的理论计算公式;DELIMONT等[17]设计提出了一系列双片段的柔性铰链,并推导了其等效刚度计算公式;文献[18]提出了用于平面折展机构的S型柔性铰链,分析了其等效刚度;文献[19]设计了一种S-LET复合型柔性铰链,并对其进行了性能分析;文献[20]设计了串联式TripIe-LET,并应用于LEMs滑块机构中。本文设计一种Deform-X柔性铰链,对弯扭耦合的柔性片段进行分析,推导其弯扭耦合等效刚度理论计算公式,并对其进行弯曲性能分析和失效分析,并设计基于Deform-X柔性铰链的平面折展四杆机构实物模型,通过仿真分析和实物测试来验证铰链的有效性和适用性。
1 Deform-X柔性铰链设计
基于文献[17]提出的混合抗拉型(Mixed tension resistant,MTR)柔性铰链[17]设计了Deform-X柔性铰链,Deform-X柔性铰链宽度为w0,长度为l0,厚度为t0,其三维结构如图1所示。
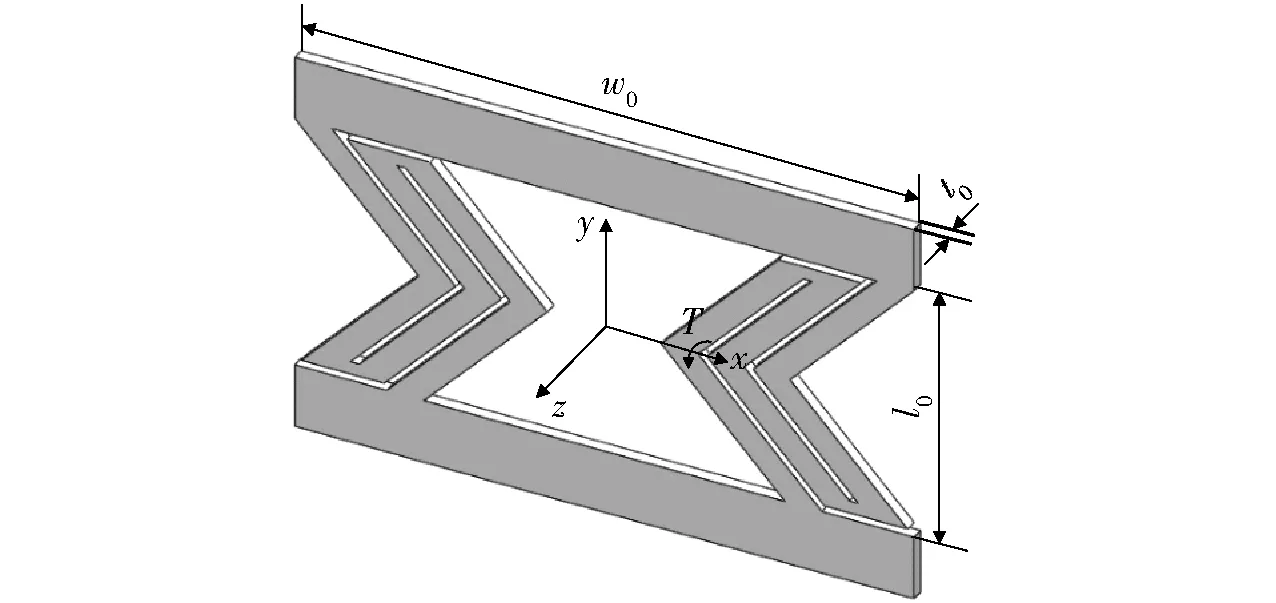
图1 Deform-X柔性铰链三维模型图Fig.1 3D model diagram of Deform-X flexure hinge
由于Deform-X柔性铰链关于y轴对称,取铰链1/2作为研究对象。根据产生的变形类型不同,Deform-X柔性铰链中的片段可以分为弯扭耦合片段、扭转片段。在图2中,片段A、B、C、D、E、F均为弯扭耦合片段,片段G、H为扭转片段,其中片段A、F的几何尺寸相同,片段B、C、D、E的几何尺寸相同,片段G、H几何尺寸相同。Deform-X柔性铰链的尺寸示意如图2所示。
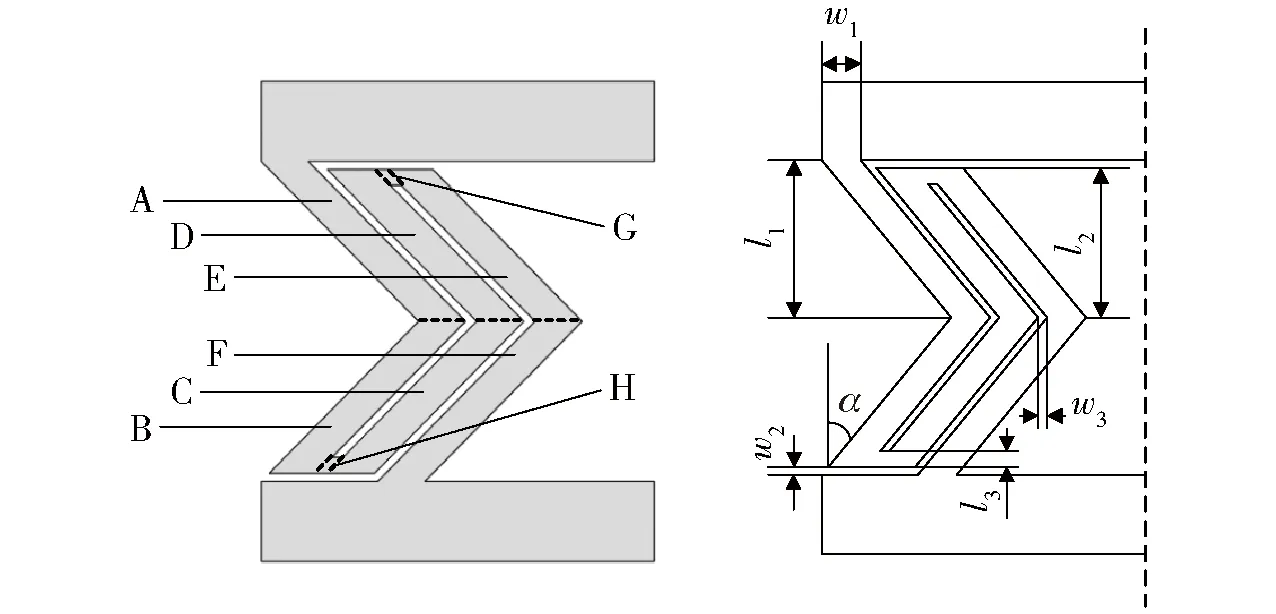
图2 Deform-X柔性铰链片段尺寸示意图Fig.2 Dimension labels of Deform-X flexure hinge
2 Deform-X柔性铰链等效刚度分析
根据柔性铰链的弹簧等效法,可以将Deform-X柔性铰链中的弯扭耦合片段等效为弯扭弹簧,将扭转片段等效为扭转弹簧,根据弹簧的串并联关系,即可得Deform-X柔性铰链的等效弹簧模型如图3所示,弯扭耦合片段有两种类型,即片段A、F的等效刚度为kBT1,片段B、C、D、E的等效刚度为kBT2,扭转片段只有一种类型,即片段G、H的等效刚度为kT。

图3 Deform-X铰链等效弹簧模型图Fig.3 Equivalent spring model diagram of Deform-X flexure hinge
根据弹簧等效的串并联关系,即可得到Deform-X柔性铰链的等效刚度为
(1)
对于弯扭耦合片段等效刚度的求解,可用微积分的思想分别求解弯曲等效刚度和扭转等效刚度,再将其进行耦合,即可得到弯扭耦合片段的等效刚度。选取片段A计算其等效刚度,设材料的弹性模量为E,剪切模量为G,泊松比为υ。
计算弯曲刚度,设片段A在转矩T作用下弯曲变形转角为θB,其微分示意如图4所示。公式推导过程为
Δy=w1
(2)
(3)
(4)

图4 片段A弯曲变形转角的微分示意图Fig.4 Differential diagram of bending angle in part A
(5)
(6)
式中kB1——片段A的弯曲等效刚度IB——片段A的转动惯量
计算扭转等效刚度,设弯扭耦合片段在转矩T作用下扭转变形转角为θT,其微分示意如图5所示。
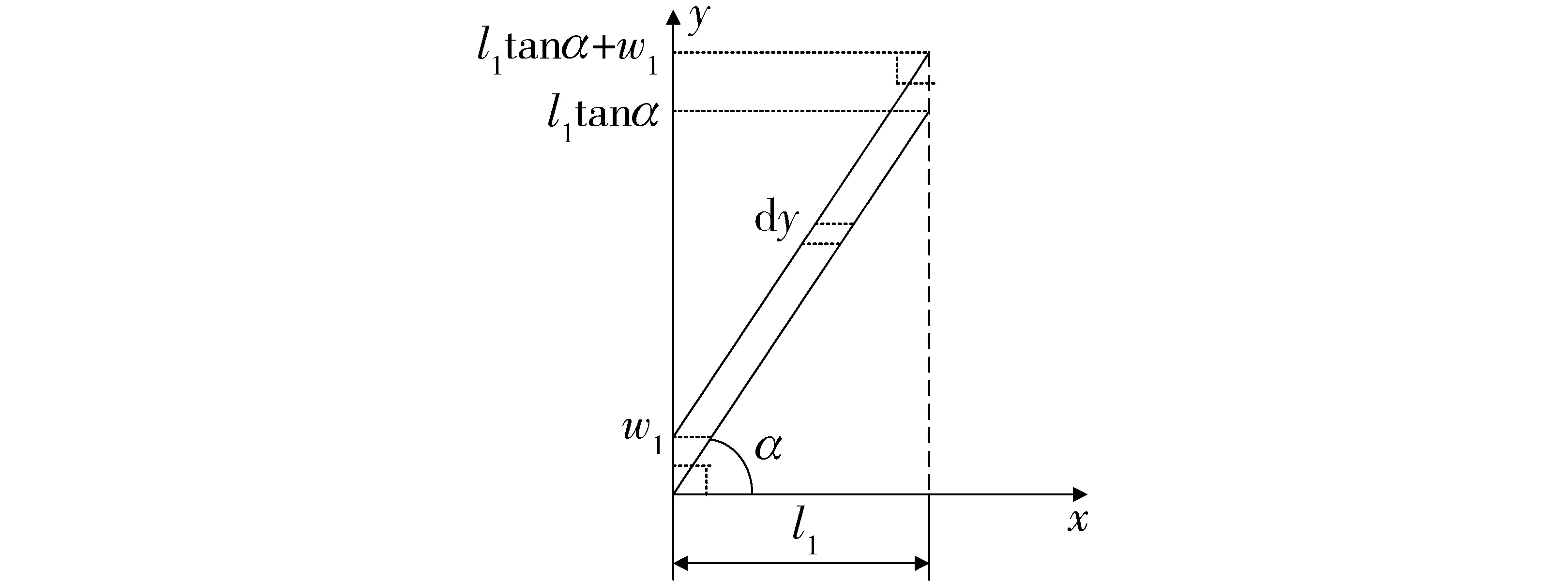
图5 片段A扭转变形转角的微分示意图Fig.5 Differential diagram of torsional angle in part A
由于弯扭耦合片段的结构特殊性,扭转等效刚度需要分为3个区间进行计算。
(1)当0 由于在0 (7) (2)当w1 (8) 其中 (9) (10) (11) Δx=w1cotα (12) (3)当l1tanα 由于在l1tanα (13) 文献[21]给出了Ki的近似公式 (14) LOBONTIU等[22]忽略了高次项,将式(14)简化为 (15) 式中LTw——扭转片段宽度t——铰链厚度 在本文中LTw=w1cotα,t=t0,则 (16) (17) 其中 (18) 根据弹簧等效耦合关系有 (19) (20) (21) 由式(20)即可得出片段A的等效刚度 kBT1= (22) 同理可以得到 kBT2= (23) 利用等效法计算kT,根据片段G、H等效刚度实例分析,可得kT的计算公式为 (24) 其中cos2αsinα为修正系数。 选取铍青铜和聚丙烯作为Deform-X柔性铰链的材料,铍青铜和聚丙烯性能参数如表1所示。 表1 铰链材料的性能参数 设计Deform-X柔性铰链的实例,选取实例的α为45°,其余尺寸参数如表2所示。 表2 Deform-X柔性铰链实例尺寸参数 根据表1和表2中参数由式(1)、(22)~(24)计算可得,铍青铜材料的Deform-X柔性铰链实例的等效刚度为keq=532.27 N·mm/rad,聚丙烯材料的Deform-X柔性铰链实例的等效刚度为keq=5.5 N·mm/rad。 Deform-X柔性铰链受到如图1所示的转矩T时,根据理论推导的等效刚度可以计算得到其弯曲变形转角θt,计算公式为 (25) 为验证理论推导的等效刚度计算公式的正确性,在ABAQUS中建立Deform-X柔性铰链设计实例的有限元仿真分析模型,施加相应的转矩T即可得到仿真分析的弯曲变形转角θs,将θt和θs对比分析,理论转角θt和仿真转角θs的相对误差为 (26) 当转矩T取不同值时,计算可以得到理论转角θt、仿真转角θs和相对误差δ如表3所示。从表3可以看出,随着转矩T的变化,Deform-X柔性铰链的理论转角θt和仿真转角θs的相对误差均在1.4%内,这证明了理论等效刚度计算公式的正确性。 表3 Deform-X柔性铰链设计实例(铍青铜)的理论转角、仿真转角及相对误差 为说明Deform-X柔性铰链的性能,选取相同外形的X型柔性铰链,即铰链宽度为w0,长度为l0,厚度为t0,铰链角度α为45°,其尺寸示意如图6所示,尺寸参数如表4所示。 图6 X型柔性铰链的尺寸示意图Fig.6 Dimension labels of X-shaped flexure hinge mm 同样利用微分的思想可以推导得到X型柔性铰链等效刚度理论计算公式为 (27) 其中 k′BT= (28) (29) 选取铍青铜作为X型柔性铰链材料,根据式(27)~(29)和表1、4中的数据,可计算得X型柔性铰链实例的等效刚度为keq=1 512 N·mm/rad。 同样,在ABAQUS中建立X型柔性铰链实例的有限元仿真分析模型,施加相应的转矩T即可得到仿真分析的弯曲变形转角θs,分别计算可以得到其弯曲变形的理论转角θt和相对误差δ。 根据计算得到的数据可以绘制出Deform-X柔性铰链和X型柔性铰链弯曲转角对比变化趋势如图7所示,同理可以得到铰链材料为聚丙烯时Deform-X柔性铰链和X型柔性铰链弯曲仿真转角对比变化趋势如图8所示。从图中可以看出,相同材料和外形尺寸的Deform-X柔性铰链和X型柔性铰链的弯曲性能差异很大,在相同转矩作用下,Deform-X柔性铰链的弯曲变形转角约为X型柔性铰链的3倍,即Deform-X柔性铰链可以在较小的转矩作用下产生较大的弯曲变形,其弯曲性能得到很大提升。 图7 铍青铜Deform-X和X型柔性铰链弯曲转角对比Fig.7 Comparison of bending angle of beryllium bronze Deform-X flexure hinge and X-shaped flexure hinge 图8 聚丙烯Deform-X和X型柔性铰链弯曲转角对比Fig.8 Comparison of bending angle of polypropylene Deform-X flexure hinge and X-shaped flexure hinge 为确定铰链的变形范围,对Deform-X柔性铰 链和X型柔性铰链进行失效分析,在ABAQUS中建立2种柔性铰链实例的有限元仿真分析模型,尺寸参数同前。 材料为铍青铜,对Deform-X柔性铰链施加转矩Tmax=360 N·mm,其应力云图如图9a所示,转角云图如图9b所示,分析数据见表5。 对铍青铜X型柔性铰链施加转矩Tmax=700 N·mm,其应力云图如图10a所示,转角云图如图10b所示,分析数据见表5。 图9 铍青铜Deform-X柔性铰链失效分析Fig.9 Failure analysis of beryllium bronze Deform-X flexure hinge 表5 Deform-X柔性铰链和X型柔性铰链失效分析数据对比 图10 铍青铜X型柔性铰链失效分析Fig.10 Failure analysis of beryllium bronze X-shaped flexure hinge 同理可得材料为聚丙烯的Deform-X柔性铰链和X型柔性铰链弯曲失效分析结果,失效分析数据见表5。 图11 平面折展四杆机构初始状态图Fig.11 Four-bar LEMs models in original state 图12 平面折展四杆机构运动状态实物图Fig.12 Four-bar LEMs of Deform-X flexure hinge in working state 设计基于Deform-X柔性铰链实例的平面折展四杆机构,材料为铍青铜,采用线切割加工,该机构实物初始状态如图11a所示,机构展开状态如图12所示。摇杆B末端位移s为37 mm时,测得角度α1为23°、α2为30°。同时,在ABAQUS中建立机构的仿真分析模型如图13所示,仿真分析得到摇杆B末端位移s为37.87 mm时角度α1为23.17°、α2为30.81°,仿真结果与实测结果基本一致,说明基于Deform-X柔性铰链的四杆机构可以实现预期运动功能。 同理,在ABAQUS中建立相同外形尺寸的基于X型柔性铰链平面折展四杆机构仿真模型如图11b所示,分析结果如图13b所示,在同样力矩作用下,该四杆机构摇杆B末端位移s为23.40 mm,角度α1为15.21°、α2为19.29°,因此,基于Deform-X柔性铰链的平面折展四杆机构变形性能优于基于X型柔性铰链的平面折展四杆机构。 (1)设计了一种Deform-X柔性铰链,分析了 图13 平面折展四杆机构运动仿真分析转角云图Fig.13 Deformation nephograms of four-bar LEMs 其弯扭耦合等效刚度,用微分法推导出Deform-X柔性铰链等效刚度的理论计算公式,通过设计实例的有限元仿真分析和理论分析结果的对比,验证了理论推导公式的正确性。 (2)通过将Deform-X柔性铰链与具有相同外形尺寸X型柔性铰链的对比,表明在相同转矩作用下,Deform-X柔性铰链可以实现更大的弯曲变形。 (3)对Deform-X柔性铰链和X型柔性铰链进行了失效分析,在相同尺寸和材料条件下,Deform-X柔性铰链的使用范围均大于X型的柔性铰链。 (4)设计了基于Deform-X柔性铰链的平面折展四杆机构的实物模型,通过实物测试和仿真分析表明Deform-X柔性铰链能够实现预期的变形,机构能够实现预期的运动。 1 HOWELL L L. Compliant mechanisms[M].New York: Wiley-Interscience,2001: 2-47. 2 于靖军, 郝广波, 陈贵敏,等. 柔性机构及其应用研究进展[J]. 机械工程学报, 2015,51(13):53-68. YU Jingjun,HAO Guangbo,CHEN Guimin,et al. State-of-art of compliant mechanisms and their applications[J]. Journal of Mechanical Engineering, 2015,51(13):53-68.(in Chinese) 3 达选祥, 勾燕洁, 陈贵敏. 一种基于变胞变换的柔顺剥线钳[J]. 机械工程学报, 2015,51(1):69-75. DA Xuanxiang,GOU Yanjie,CHEN Guimin. Compliant wire stripper based on metamorphic transformation[J]. Journal of Mechanical Engineering, 2015,51(1):69-75.(in Chinese) 4 余跃庆, 崔忠炜, 赵鑫,等. 柔顺关节并联机器人设计与实验[J/OL]. 农业机械学报, 2013, 44(7):274-278.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130747&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2013.07.047. YU Yueqing,CUI Zhongwei,ZHAO Xin,et al.Design and experiment of parallel robot with compliant joints[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(7):274-278.(in Chinese) 5 余跃庆, 马兰, 崔忠炜,等. 并联机器人开槽薄壁柔顺关节设计与实验[J/OL]. 农业机械学报, 2014, 45(5):284-290. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140544&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2014.05.044. YU Yueqing,MA Lan,CUI Zhongwei, et al.Design and experiment of open thin-walled flexure joints of parallel robot[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5):284-290.(in Chinese) 6 MAGLEBY S P, ALBRECHTSEN N B, HOWELL L L. Using lamina emergent mechanisms to develop redit-card sized products[C]∥ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2011:223-231. 7 SMITH S T. Flexures: elements of elastic mechanisms[M]. Boca Raton, FL: CRC Press, 2000. 8 LOBONTIU N. Compliant mechanisms: design of flexure hinges[J]. Boca Raton, FL: CRC Press, 2003:93. 9 JACOBSEN J O, WINDER B G,HOWELL L L, et al. Lamina emergent mechanisms and their basic elements[J]. Journal of Mechanisms & Robotics, 2010, 2(1):298-320. 10 MAGLEBY S P, HOWELL L L, GOLLNICK P S, et al. A preliminary study of actuation approaches for lamina emergent mechanisms[C]∥ASME International Design Engineering Technical Conferences, 2011:191-202. 11 ATEN Q T, ZIRBEL S A, JENSEN B D, et al. A numerical method for position analysis of compliant mechanisms with more degrees of freedom than inputs[J]. Journal of Mechanical Design, 2010, 133(6):491-502. 12 WILDING S E, HOWELL L L, MAGLEBY S P. Spherical lamina emergent mechanisms[J]. Mechanism & Machine Theory, 2011, 49(3):187-197. 13 JACOBSEN J O, HOWELL L L, Magleby S P, et al. Components for the design of lamina emergent mechanisms[C]∥ASME 2007 International Mechanical Engineering Congress and Exposition, 2007:165-174. 14 JACOBSEN J O, CHEN G, HOWELL L L, et al. Lamina emergent torsional (LET) joint[J]. Mechanism & Machine Theory, 2009, 44(11):2098-2109. 15 MAGLEBY S P, FERRELL D B, ISAAC Y F, et al. Development of criteria for lamina emergent mechanism flexures with specific application to metals[J]. ASME Journal of Mechanical Design, 2011, 133(3):586-599. 16 DELIMONT I L, MAGLEBY S P, HOWELL L L. Evaluating compliant hinge geometries for origami-inspired mechanisms[J]. Journal of Mechanisms & Robotics, 2015, 7(1):331-341. 17 DELIMONT I L, MAGLEBY S P, HOWELL L L. A family of dual-segment compliant joints suitable for use as surrogate folds[J]. ASME Journal of Mechanical Design, 2015, 137(9):092302-092302-9. 18 邱丽芳,孟天祥,张九俏,等.平面折展机构S形柔性铰链设计与试验[J/OL]. 农业机械学报,2014, 45(9):324-328.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140952&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2014.09.052. QIU Lifang,MENG Tianxiang,ZHANG Jiuqiao,et al.Design and test of lamina emergent mechanisms S-shaped flexure hinge[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2014, 45(9):324-328.(in Chinese) 19 邱丽芳,庞大千,陈家兴,等. S-LET复合型柔性铰链设计与性能研究[J/OL]. 农业机械学报, 2016,47(2):408-412.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160255&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.02.055. QIU Lifang,PANG Daqian,CHEN Jiaxing,et al. Design and performance analysis of lamina emergent mechanisms S-LET-shaped flexure hinge[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016,47(2):408-412.(in Chinese) 20 邱丽芳,印思琪,谢仲添,等. 基于串联式TripIe-LET的LEMs滑块机构分析[J/OL]. 农业机械学报, 2016,47(6):381-386. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160650&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.06.050. QIU Lifang,YIN Siqi,XIE Zhongtian,et al. Analysis of lamina emergent slider mechanisms based on series Triple-LET[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016,47(6):381-386.(in Chinese) 21 PORTER L E, TRZASKA W H.Formulas for stress and strain[M]. 北京:清华大学出版社,2003. 22 LOBONTIU N, GARCIA E, CANFIELD S. Torsional stiffness of several variable rectangular cross-section flexure hinges for macro-scale and MEMS applications[J]. Smart Materials & Structures, 2004, 13(13):12-19. Design and Analysis of Deform-X Flexure Hinge QIU Lifang WANG Dong YIN Siqi YANG Debin (SchoolofMechanicalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China) Deform-X flexure hinge was designed, and its equivalent stiffness was analyzed by using differential methods, and the theoretical calculation formula of the equivalent stiffness of Deform-X flexure hinge was derived. Through theoretical analysis and ABAQUS simulation analysis of Deform-X flexure hinge in a size, the correctness of calculation formula of the equivalent stiffness of Deform-X flexure hinge was verified. By comparing the performance of X-shaped flexure hinge with the same shape and size as the Deform-X flexure hinge, the bending deflection angle of the Deform-X flexure hinge was about three times of that of the X-shaped flexible hinge under the same torque. Bending failure analysis of X-shaped flexure hinge and Deform-X flexure hinge was carried out, and the results showed that the available using range of Deform-X flexure hinge was wider than that of X-shaped flexure hinge. The four-bar mechanism model based on Deform-X flexure hinge was manufactured. The test and simulation analysis showed that the Deform-X flexure hinge can realize the expected deformation. In addition, the four-bar mechanism model based on X-shaped flexure hinge was established in ABAQUS. Through the comparative simulation analysis, in the case of the same size, the bend deformation performance of four-bar mechanism based on Deform-X flexure hinge was better than that of four-bar mechanism based on X-shaped flexure hinge. flexure hinge; bending-torsional coupling; equivalent stiffness; failure analysis; four-bar mechanism 10.6041/j.issn.1000-1298.2017.04.049 2016-07-25 2016-09-05 国家自然科学基金项目(51475037) 邱丽芳(1966—),女,教授,主要从事机械设计及理论和柔顺机构研究,E-mail: qlf@ustb.edu.cn 杨德斌(1965—),男,教授,博士生导师,主要从事机械设备状态评价及无线传感器研究,E-mail: ydb@ustb.edu.cn TH122 A 1000-1298(2017)04-0370-073 Deform-X柔性铰链实例计算与分析



4 Deform-X与X型柔性铰链的性能比较
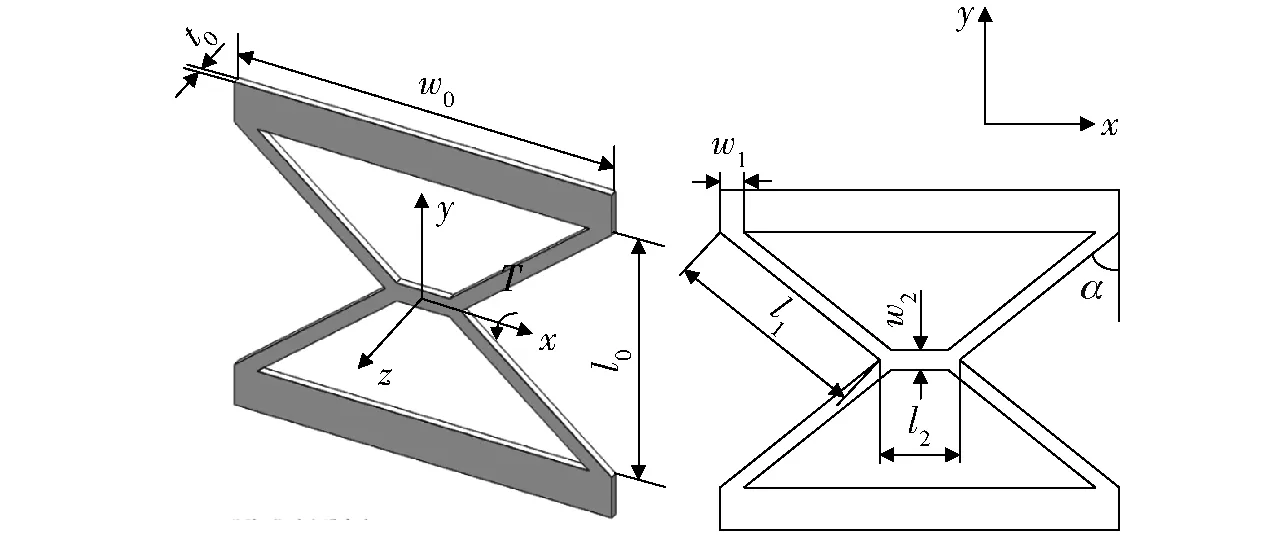

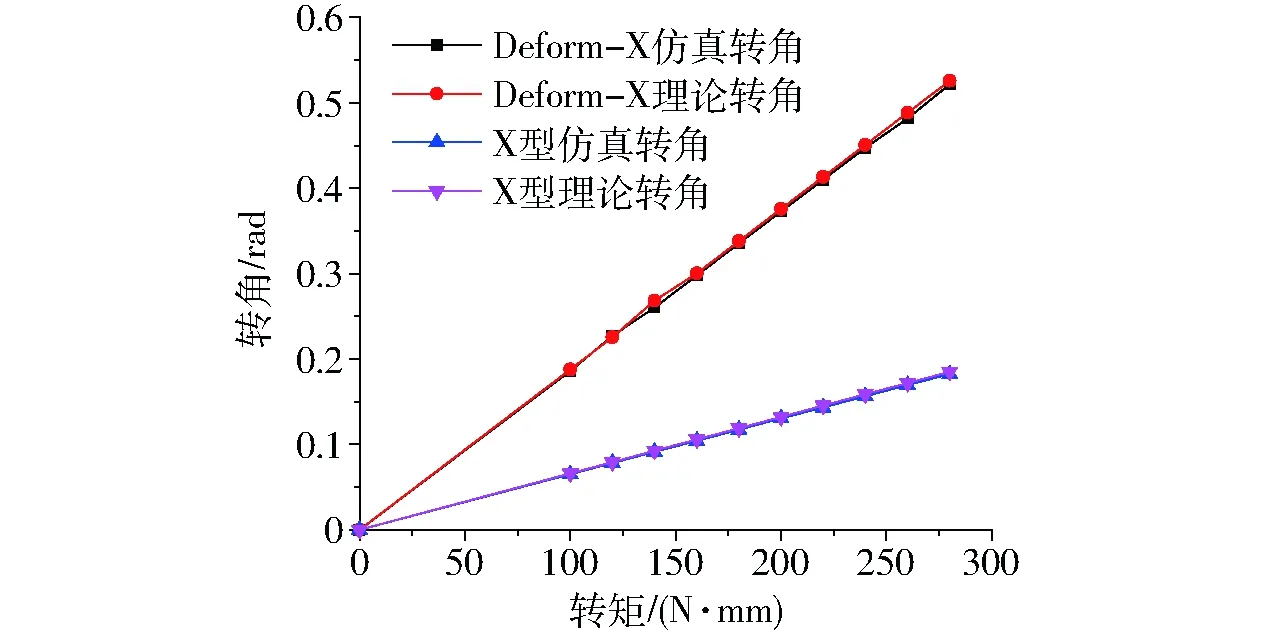
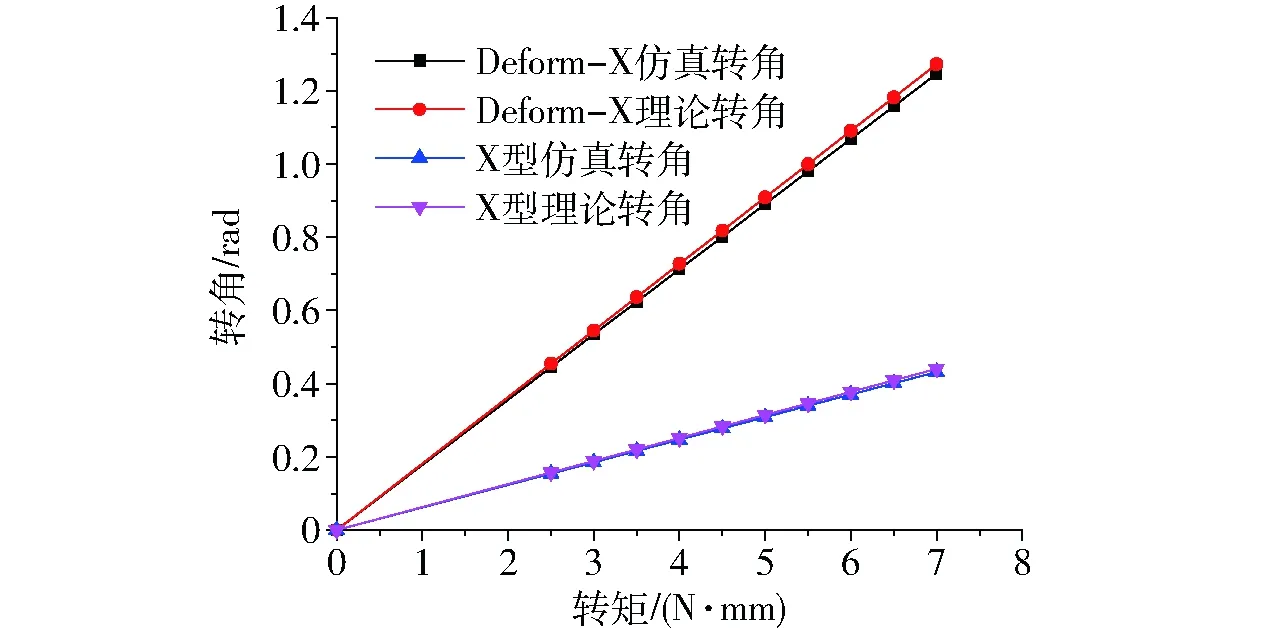
5 Deform-X与X型柔性铰链的失效分析


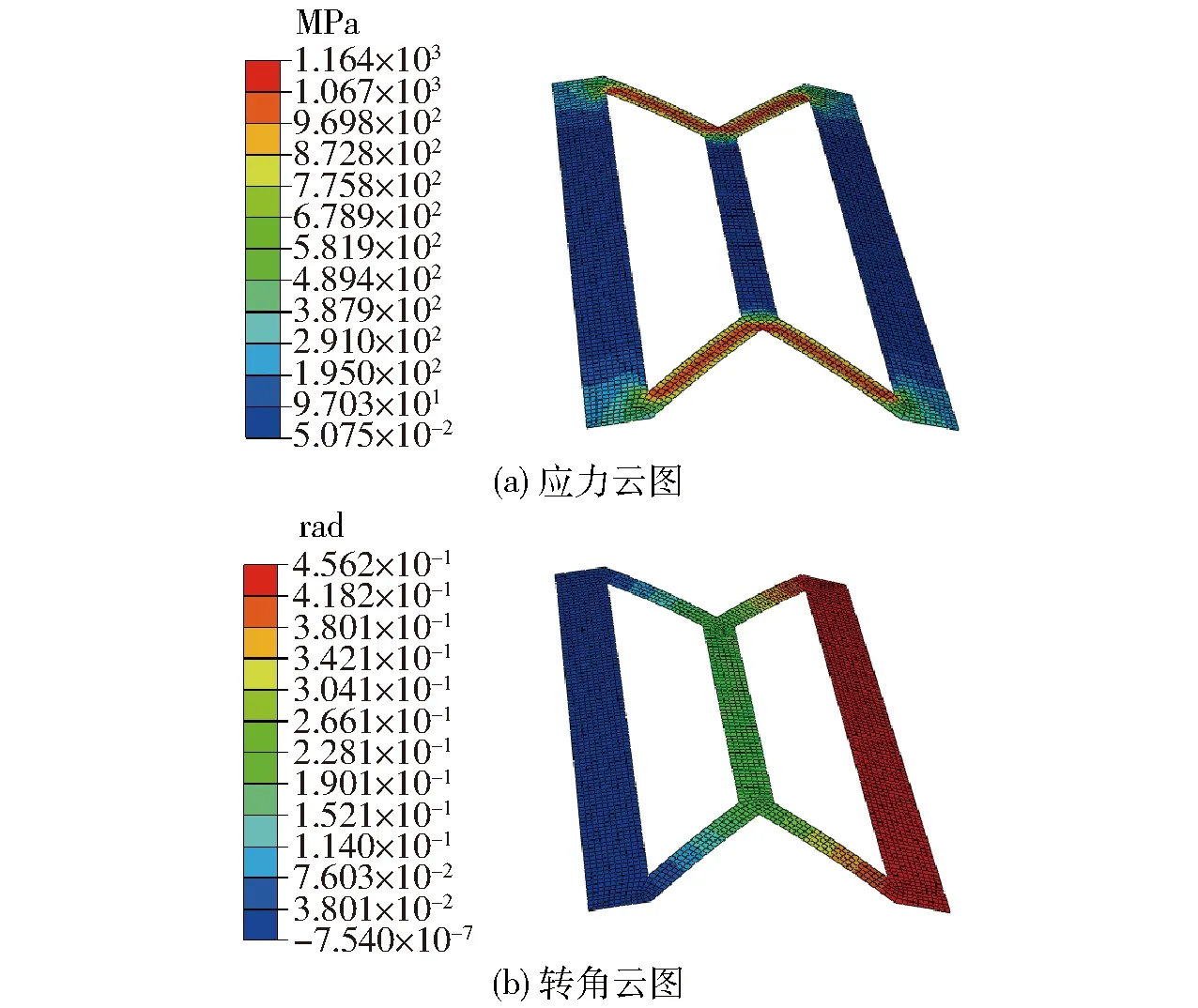
6 基于Deform-X与X型柔性铰链的四杆机构


7 结论

