具有不可关联性的承诺方案

马 丽，窦家维，吴艳梅

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

具有不可关联性的承诺方案

马 丽，窦家维，吴艳梅

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

承诺方案是密码学中的一个基本方案，在密码学中的其他协议中有重要的应用，比如：安全多方计算、加密方案、签名方案、密钥交换协议等。不可关联的承诺方案是国际密码学界的一个研究热点，是实现电子拍卖的理论基础，也是多方保密计算一个重要的模块。不可关联承诺方案在密码学与实际应用中有很多用途，目前的研究主要集中于提高不可关联承诺方案的安全性、效率以及减弱困难性假设等方面。因此，提出了两种不可关联承诺方案，能有效地阻止关联攻击和复制攻击，且与其他方案相比效率更高。两种不可关联承诺方案分别基于离散对数假设和哈希函数性质的合理应用，如果能成功实施关联攻击就能够计算离散对数，计算离散对数在密码学中是难解问题，随后给出了详细的安全性证明和效率分析。研究分析表明，不可关联承诺方案运用哈希函数作为承诺函数，效率以及安全性都比较高。

不可关联承诺；离散对数假设；哈希函数；承诺函数

0 引 言

在保密拍卖中，拍卖方发布拍卖公告，公告拍卖商品的展示时间与拍卖截止时间。在拍卖截止时间之前，竞价者写好自己的出价，装入信封并密封。截止日期过后，拍卖者在约定的开标时间，当着所有竞价者的面打开信封，出价最高者获得拍卖的商品。这是现实社会的拍卖过程。如果拍卖活动在网上进行，就成为网络拍卖。无论现实拍卖还是网络拍卖，都要保密进行。现实拍卖需要密封信封，密封信封的数字化对应物就是数字承诺[1]。

承诺协议分为两个阶段，承诺阶段和揭示承诺阶段。在承诺阶段，承诺者根据自己的价格v，选择一个随机数r，计算承诺函数c=c(v,r)并发送给接收者，相当于把出价装入密封信封。在这个阶段，要求任意概率多项式时间的接收者都不能得到关于承诺值v的任何知识，即使接收者试图进行欺骗，也无法得到相应知识，这个性质称其为隐藏性。在揭示承诺阶段，承诺者向接收者提供随机数r和自己的承诺值v，接收者计算承诺函数c'=c(v,r)，如果c=c'，原承诺有效，否则拒绝，这个阶段相当于当面打开信封。在这个阶段，要求任意概率多项式时间的承诺者无法找到v≠v',r≠r'使得c(v,r)=c(v',r')，这个性质称其为绑定性。

然而，一般的承诺协议具有可关联性。假设Bob是关联攻击者，他不知道Alice的v，但可以利用Alice的c(v)得到c(v*)(v*=v+b)。如果这样，在拍卖中Bob就可以用比Alice高一点的价格获得拍卖商品，这是不公平的。为了克服关联承诺造成的不公平，Dolev等提出了不可关联承诺的概念[2]，并提出了一个著名的不可关联承诺方案，其他学者也提出了一些不可关联承诺方案[3-11]，但这些方案的效率都有待进一步提高。

因此，基于离散对数假设和哈希函数的性质，构造了两种不可关联承诺方案。这两种方案简单易行，安全性和效率都很高，计算复杂性和通信复杂性很低，可以作为其他密码学协议的模块并广泛应用于其他实际安全问题中。

1 预备知识

1.1 难解问题

现代密码学的安全性基于某些困难问题假设。难解问题是这样一些问题，经过长时间研究，人们没有找到这些问题的多项式时间算法或概率多项式时间算法，但也不能证明这些问题不存在多项式时间算法或者概率多项式时间算法。密码系统的设计要使得攻击者在不知道有关机密信息时，对密码系统实施成功攻击，必须要解某个难题。密码学中的困难性问题主要有因子分解、离散对数、判断n次剩余类问题[12]。

1.2 离散对数假设

αx≡βmodp

(1)

(2)

1.3 数字承诺方案

要理解数字承诺方案，需要理解两个概念：安全性或隐藏性(secrecy or hiding)和歧义性(ambiguity)。

安全性：接收者即使任意偏离协议，也不能区分对于v的承诺c=c(v,r)和对于v'的承诺c'=c(v',r')，安全性保护承诺者的利益。

定义1[13]：数字承诺方案是概率多项式承诺者与接收者之间的一个交互协议，其中承诺者的输入为v，协议同时满足安全性和无歧义性。

1.4 基于离散对数假设的数字承诺方案

基于离散对数假设的数字承诺方案由Pedersen提出[14]，承诺协议如下：

揭示承诺：承诺者将v,r发送给接收者，接收者验证下述等式是否成立：

如果等式成立，承诺有效；否则无效。

(4)

Bob看到了承诺者揭示的承诺值(v,r)后，他可以将(v+b,r+m)作为他的承诺值进行揭示，没有人有理由怀疑他的承诺。如果攻击者Bob这样做，对于Alice是非常不公平的。为克服此承诺方案的可关联问题，防止关联攻击，Dolev等提出了不可关联承诺的概念[2]。

1.5 不可关联承诺

有趣关系(interesting relation)：如果一个关系R⊆M×M是多项式时间可计算的非自反关系，则这个关系是有趣的。

不可关联承诺：假设攻击者知道v的承诺c=c(v,r)，仍然不能计算v*的承诺c*=c(v*,r')((v,v*)∈R)，则这个承诺称为不可关联承诺。

不可关联承诺有如下两种：

(1)关于承诺的不可关联。

一个具有多项式计算能力的攻击者知道关于v的承诺c=c(v,r)，只要能做出一个关于v*的承诺((v,v*)∈R)，不管他是否能够成功地揭示这个承诺，都认为关联成功。

一个承诺方案是关于承诺可关联的，如果一个多项式计算能力的攻击者能够在这种意义下关联成功。若任何具有多项式能力的攻击者都不能在这种意义下关联成功，就称承诺方案是关于承诺不可关联的。

(2)关于揭示的不可关联。

一个具有多项式计算能力的攻击者知道关于v的承诺c=c(v,r)，能够做出一个c*=c(v*,r')((v,v*)∈R)，且能够在揭示阶段成功地揭示该承诺，才算关联成功。一个承诺方案是关于揭示可关联的，如果一个多项式计算能力的攻击者在这种意义下关联成功。若任何具有多项式能力的攻击者都不能在这种意义下关联成功，称承诺方案是关于揭示的不可关联。

如果一个承诺方案是关于承诺不可关联的，那么它也一定是关于揭示不可关联的。

1.6 Fischlin提出的不可关联承诺方案

Fischlin提出了一个著名的不可关联承诺方案[15]，该方案的思想是对协议1进行改进，要求承诺者在做出承诺之后，再用零知识证明的方法向接收者证明他确实知道他的承诺值。如果是真正的承诺者就容易证明，而攻击者就无法完成零知识证明过程，因而无法完成承诺。协议如下：

1)承诺阶段。

将M,A,S发送给接收者。

(2)接收者选择b∈Zp，并将b发送给承诺者。

2)揭示承诺阶段。

(1)承诺者计算:

将a,u,r,y,z,v发送给接收者。

(2)接收者计算:

c≡a+bmodp

(3)接收者验证:

若相等，则接受承诺；否则拒绝承诺。

协议1具有可关联性，可能导致拍卖失败，造成经济损失。协议2中用附加零知识证明的方法解决了协议1中存在的关联性问题，但是零知识证明的计算复杂性和通信复杂性都较高，因而效率较低。为提高不可关联承诺的效率，设计了两种不可关联承诺方案。

2 两种不可关联承诺方案

2.1 基于离散对数的方案

协议3：基于离散对数的承诺方案。

c(v)=(c1,c2,c3)=(gxmodp,gymodp,xv+2yamodp)

将c发送给接收者作为对v的承诺。

揭示承诺阶段：承诺者把x,y发给接收者，接收者验证:

(gxmodp,gymodp,xv+2yamodp)=(c1,c2,c3)

如果成立，则接受承诺；否则拒绝承诺。

直觉上，承诺者承诺的值是x的一个指数，攻击者要想做出一个关于v+b的承诺，需要给c3乘以xb，这就必须知道x。要知道x，就必须求解离散对数。但求离散对数是困难的，所以该方案是不可关联的。关于不可关联性，有定理如下：

定理1：协议3构成一个承诺方案且是关于揭示不可关联的。

要证明协议3构成一个数字承诺方案，需要下面的引理。

证明:首先证明安全性，假设对于v的承诺是：

(c1,c2,c3)=(gxmodp,gymodp,x(v+2)yamodp)

对于v'的承诺是：

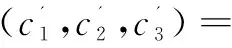
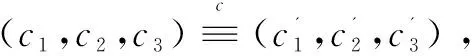
当Carol揭示承诺时，需要揭示s,t,v+1的值，就可以利用s,t,v计算α。

因为

所以

在这个方程中s,t,y,v都是已知的，都可以从方程中消除，最后得到一个xv+2modp≡u。利用费马小定理可以很容易求出x=umodp。而根据离散对数假设，这是不可能的。所以方案是关于揭示不可关联的。事实上，这个方案也是关于承诺不可关联的。遗憾的是，目前还不能把它标准归约到离散对数问题。

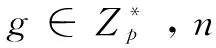
协议4:拍卖协议。

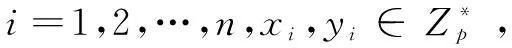
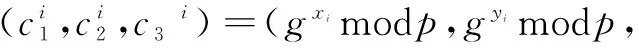
发送给拍卖者作为自己的秘密出价。

2.2 基于Pedersen的数字承诺方案的改进

协议设计：协议2是在协议1的基础上增加零知识证明过程来阻止可能的关联攻击，注意到不用零知识证明的方法也可以阻止关联攻击，设计了一个基于单向散列函数的不可关联承诺协议，就是在协议1的基础上添加单向散列函数，同时将单向散列函数值作为承诺的一部分，使得承诺方案具有不可关联性。具体协议如下：

c2=c2(v,r)=hash(v‖r)

并将(c1,c2)发送给接收者。

揭示承诺阶段：承诺者发送(v,r)给接收者，接收者验证下述等式是否成立：

c2=c2(v,r)=hash(v‖r)

如果等式成立，则接受承诺值v；否则拒绝承诺值。

协议的正确性：

协议1是著名的承诺方案，文献[10]已经证明它确实构成一个承诺方案。这里只证明增加单向散列函数确实能够阻止关联攻击。

关联攻击者在看到(c1,c2)后，要想做出对v+b的承诺，必须选择一个m,并计算：

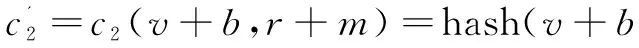
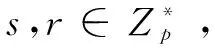
c2=hash(x||r)

作为对x的承诺，把(c1,c2)给攻击者。攻击者得到(x+b,r+m)，就可以得到x。但根据离散对数假设，这是不可能的。

3 性能分析

Fischlin等提出了协议2，主要利用零知识证明的方法，使得承诺方案具有不可关联性；分别利用离散对数和和哈希函数的性质提出了两种不可关联性的承诺方案；这里对协议2和两种不可关联承诺方案的计算复杂性和通信复杂性进行分析。

3.1 计算复杂性

在利用公钥密码系统构建的协议中，模指数运算的次数是决定协议效率的主要因素，因此协议的计算复杂性常常用模指数运算的次数衡量。一个协议需要的模指数运算次数越多，其计算复杂性越高，效率就越低。对这三种协议的计算复杂性，主要分析其模指数运算，而忽略计算复杂度低得多的模加法运算、单向散列函数运算等。协议2需要进行12次模指数运算，而协议3需要6次，协议5需要进行2次。

3．2 通信复杂性

协议的通信复杂性是传递数据的次数与传送数据的比特数。传递的次数越多，则协议的通信复杂性越高。传递的比特越多，通信复杂性也越高。协议2中，通过3次传递完成了承诺和承诺的揭示过程，需要传送的比特数为10lgp。协议3中，通过2次传递完成了数据的承诺与承诺揭示，需要传送的比特数为2lgp。协议5中，通过2次传递完成了数据的承诺与承诺揭示，传递的比特数为lgp。(单向散列函数值的比特数通常比lgp的比特数少得多，因此可以忽略)

3.3 协议对比

计算复杂性与通信复杂性的全面比较见表1。表中计算复杂性指模指数运算的次数，通信复杂性指通信次数与传递数据的比特数。

表1 三种不可关联性承诺的性能分析

4 结束语

由于不可关联承诺方案有很多实际应用，提出了两种新的不可关联承诺方案。协议3是基于离散对数直接构造的方案，具有不可关联性；协议5运用哈希函数，将Pedersen的基于离散对数假设的关联承诺方案改进为一个不可关联性承诺方案，并且提高了安全性。承诺方案的关键问题是如何找到简单的承诺函数。因此，如何找到简单的承诺函数并设计高效的承诺方案，是今后主要的研究方向。

[1] Hofheinz D,Quade J M.Universally composable commitments using random oracles[M]//Theory of cryptography.Berlin:Springer,2004:58-76.

[2] Dolev D,Dwork C,Naor M.Nonmalleable cryptography[J].SIAM Review,2003,45(4):727-784.

[3] Dachman-Soled D,Malkin T,Raykova M,et al.Adaptive and concurrent secure computation from new adaptive,non-malleable commitments[C]//Advances in cryptology-ASIACRYPT 2013.[s.l.]:[s.n.],2013:316-336.

[4] Abdalla M,Benhamouda F,Blazy O,et al.SPHF-friendly non-interactive commitments[C]//Advances in cryptology-ASIACRYPT 2013.[s.l.]:[s.n.],2013:214-234.

[5] Li Shundong,Wang Daoshun,Dai Yiqi,et al.New method for constructing non-malleable commitment schemes[J].Chinese Journal of Electronics,2008,17(4):583-588.

[6] Ishai Y, Kushilevitz E, Ostrovsky R.Sufficient conditions for collision-resistant hashing[M]//Theory of cryptography.Berlin:Springer,2005:445-456.

[7] Haitner I, Nguyen M H, Ong S J,et al.Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function[J].SIAM Journal on Computing,2009,39(3):1153-1218.

[8] Brenner H,Goyal V,Richelson S,et al.Fast non-malleable commitments[C]//Proceedings of the 22nd ACM SIGSAC conference on computer and communications security.[s.l.]:ACM,2015:1048-1057.

[9] Pass R.Unprovable security of perfect NIZK and non-interactive non-malleable commitments[M]//Theory of cryptography.Berlin:Springer,2013:334-354.

[10] Naor M.Bit commitment using pseudorandomness[J].Journal of Cryptology,1991,4(2):151-158.

[11] Goldreich O. Foundations of cryptography:basic tools[M].London:Cambridge University Press,2001.

[12] 李顺东,王道顺.现代密码学[M].北京:科学出版社,2009.

[13] Paillier P.Public-key cryptosystems based on composite degree residuosity classes[C]//Advances in cryptology-EUROCRYPT’99.[s.l.]:[s.n.],1999:223-238.

[14] Pedersen T P.Non-interactive and information-theoretic secure verifiable secret sharing[C]//Advances in cryptology-CRYPTO’91.[s.l.]:[s.n.],1992:129-140.

[15] Fischlin M,Fischlin R.Efficient non-malleable commitment schemes[C]//Advances in cryptology-CRYPTO 2000.[s.l.]:[s.n.],2000:413-431.

Non-malleable Commitment Schemes

MA Li,DOU Jia-wei,WU Yan-mei

(College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China)

Commitment scheme is a basic scheme in cryptography and has been important application in other agreements of cryptography like secure multi-party computation,encryption scheme,signature scheme,key exchange protocols and so on.Non-malleable commitment scheme is one focus in the international cryptographic community and the theoretical basis of electronic auction,which is also an important building block of secure multi-party computation and has important applications in cryptography and practice.At present,most studies focus on improving the security and the efficiency of non-malleable commitment schemes and less difficulty hypothesis,etc.So,two non-malleable commitment schemes are proposed which can efficiently prevent malleable attack and copy attack.These non-malleable commitment schemes are constructed based on discrete logarithm assumption and one-way hash function.If adversary can successfully attack the scheme,it can compute the discrete logarithm.The computing discrete logarithm in cryptography is a hard problem,and its security proving and efficiencies analysis are given.Study analysis shows that non associated commitment scheme using hash function as a commitment function,efficiency and security are relatively high.

non-malleable commitment;discrete logarithm assumption;hash function;commitment function

2016-06-07

2016-09-15 网络出版时间：2017-03-07

国家自然科学基金资助项目(61272435)

马 丽(1983-)，女，硕士研究生，研究方向为密码学与信息安全；窦家维，副教授，硕士生导师，研究方向为密码学与信息安全。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0922.070.html

TP301

A

1673-629X(2017)05-0108-05

10.3969/j.issn.1673-629X.2017.05.023