基于双稀疏字典的新型盲压缩感知模型

钱 阳，李 雷，石曼曼

(南京邮电大学 视觉认知计算与应用研究中心，江苏 南京 210023)

基于双稀疏字典的新型盲压缩感知模型

钱 阳，李 雷，石曼曼

(南京邮电大学 视觉认知计算与应用研究中心，江苏 南京 210023)

针对压缩感知理论实际应用过程中，稀疏基先验信息未知的情况下，如何从信号的压缩测量值中学习与待重构信号本身相适应的字典的同时，利用该字典重构出原始信号的问题，基于已有的盲压缩感知理论(BCS)，在稀疏基为双稀疏字典结构的约束条件下，提出了一种新型的盲压缩感知算法(D-BCS)。所提算法交替执行稀疏编码阶段和字典更新阶段。在稀疏编码阶段，采用分裂Bregman迭代求解非凸的l1最小化问题，从而实现稀疏系数矩阵的更新；而在字典更新阶段，则通过将目标优化函数转化为类LASSO问题，并利用LASSO算法来实现字典原子的逐列更新。在不同采样率下，对多个测试视频帧进行仿真对比实验，实验结果表明，所提算法能很好地从压缩测量值中恢复出原始信号，且表现出了最佳的性能改进。

盲压缩感知；双稀疏字典；分裂Bregman迭代；LASSO；稀疏表示

0 引 言

近年来，以信号的稀疏性先验求解图像反问题吸引着学者们的广泛关注[1-2]，尤其是压缩感知(Compressed Sensing,CS)领域[3]。CS理论主要包括信号的稀疏表示、观测矩阵的选取和信号重构这三个阶段。其中，稀疏表示是压缩感知理论应用的前提和基础，它决定了图像反问题的求解质量。目前，稀疏化方法主要分为两种：解析方法和学习方法。前者是基于固定正交基的变换，如DCT变换、傅里叶变换等；而后者则是根据信号本身来学习过完备字典，再对信号进行稀疏化，如K-SVD字典学习算法[4]。现有的CS算法一般都是建立在稀疏基已知的先验条件下，因此信号的先验信息至关重要。然而，在实际应用过程中，信号的信息往往无法被事先获知，能否根据信号的测量值学习与待重构信号本身相适应的字典并利用该字典重构出原始信号，是压缩感知领域急需解决的问题[5]。

近几年，Gleichman等[6]提出的盲压缩感知(Blind Compressed Sensing,BCS)理论，为稀疏表示领域的研究提供了一个全新的视野。该理论的思想是省略了信号的稀疏表示过程，在采样和重构阶段避免对信号先验知识的完全掌握，而是通过对稀疏基施加适当的约束条件来实现信号的唯一重构。目前，对BCS的研究仍处于理论发展初期，只有少量的文献给出了直接根据测量值训练字典的具体算法，如CK-SVD(Compressive K-SVD)[7]算法和CDL(Compressive Dictionary Learning)[8]算法，这两种算法均是基于稀疏基为双稀疏字典的约束条件来实现信号的唯一重构。

基于已有的BCS理论，在稀疏基为双稀疏字典的约束条件下，提出了一种新型的盲压缩感知算法(D-BCS)。该算法交替执行稀疏编码阶段和字典更新阶段，在稀疏编码阶段，利用Split Bregman迭代对稀疏表示系数矩阵进行求解，而在字典更新阶段，将字典更新优化问题通过误差最小准则转化为可用LASSO求解的最小化问题，从而实现字典原子的更新。将所提算法用于视频帧图像的重构中，实验结果表明，该算法能有效地从压缩测量值中重构出视频帧，且重构性能较好。

1 背景知识

1.1 盲压缩感知模型

(1)

其中，‖‖0为l0范数，表示向量中非零元素的个数。

s.t.∀i,‖ai‖0≤T0

(2)

其中，T0为稀疏表示系数中非零分量数目的上限。

通过引入正则化参数λA，式(2)可以转化为无约束最优化问题：

(3)

由于l0范数模型是NP难题[12]，在多项式时间内只能求得次优解。一种最常用的做法是采用l1范数来最佳凸逼近l0范数，则BCS模型可转化为如下的优化问题

(4)

其中，‖‖1为l1范数，表示向量中所有元素的绝对值之和。

然而，BCS的信号重构问题(4)在数学上是一个严重的病态问题，必须给字典D施加额外的约束条件，才能保证信号的唯一性重构。文献[6]中讨论了三种情况：D为从已知的正交基中根据重构残差最小准则选择出的一个正交基；D为双稀疏字典；D具有正交对角结构化特点。此外，Silva等研究了另一种情况：D为多个子字典的联合，且每个子字典的原子相互正交，待恢复的信号只用其中的某个子字典表示。若字典D满足以上4个条件之一且观测矩阵Φ满足相应的条件，则BCS有唯一解。

1.2 分裂Bregman迭代算法(SBI)

由Goldstein等[13]提出的分裂Bregman迭代算法，最初是用来解决TV-L1模型的图像扩散问题。该算法结合了Split算法和Bregman迭代的优点，能够在提高图像处理质量的同时保证高效的计算效率，在图像处理领域应用极其广泛[14-15]。

SBI算法解决的是如下的约束优化问题：

(5)

其中，G∈RN×M，f:RN→R，g:RM→R是凸函数。

SBI算法对问题(5)的具体求解步骤如下：

初始化:设置t=0，b0=0，u0=0，v0=0，选择参数μ>0

Repeat

b(t+1)=b(t)-(u(t+1)-Gv(t+1))

t←t+1

Until满足停止迭代条件

1.3 双稀疏字典

双稀疏字典结构是在一个已知基字典的基础上再构造一个具有稀疏原子的字典，即定义：D=ΨΘ。其中，Ψn×n是一个基字典，Θn×k(n≤k)是字典结构的稀疏表示系数矩阵。该模型表明字典的每个原子都有它相应的在某个指定基字典上的稀疏表示。对于Θ的构造，显而易见，若Θ为单位矩阵，则字典D退化为普通基。与文献[8]一样，将Θ定义为如下形式：

(6)

其中，δ=k-n；约束Θ(或Σ)为稀疏矩阵。

文献[8]指出，这种约束能以任意形式保存所学习的字典且使字典不易受过匹配的影响。

2 算法设计与分析

所提基于双稀疏字典的新型盲压缩感知算法的数学模型如式(7)所示：

(7)

其中,λΘ为正则化参数。

与字典学习方法类似，可以通过交替执行稀疏编码阶段和字典更新阶段来求得此优化模型的最优解。

2.1 稀疏编码阶段

该阶段对压缩测量值的稀疏表示系数A进行求解。此阶段，固定双稀疏字典D(t)，亦即固定字典结构的稀疏表示系数矩阵Θ(t)，其所求优化模型如式(8)所示：

(8)

对于式(8)的求解，采用上一节中介绍的分裂Bregman迭代法。通过引入变量u，首先将式(8)转化为等价的约束形式：

s.t.u=ΨΘA

(9)

(10)

(11)

b(t+1)=b(t)-(u(t+1)-ΨΘ(t)A(t+1))

(12)

因此，最小化问题(8)的求解进一步转化为对子问题u和A的求解。接下来，将分别给出两个子问题的具体求解过程。

2.1.1u子问题

给定Θ(t)和A(t)，不难看出，u子问题是一个关于u的最小二乘问题，其有解析解，通过简单的计算，可以得到：

(13)

(14)

将式(14)代入式(10)中，则有：

(15)

式(15)是一个简单的最小二乘问题，且其解析解为：

(16)

2.1.2A子问题

给定u(t+1)，根据式(11)，A子问题可演变成如下形式：

(17)

其中，r(t+1)=u(t+1)-b(t)。

其中，正则化参数λA的选取依赖于压缩样本的噪声水平以及待重构图像的复杂度。当λA取值较大时，A(t+1)中只能包含图像块的重要组成部分，这对高噪声情况非常适用；而当λA取值较小时，稀疏表示系数A(t+1)中将会包含每个图像块过多的细节信息，这些冗余的细节信息将会使得学习过程混乱，且容易导致算法发散。因此，选择合适的正则化参数λA至关重要。

不难发现，式(17)是一个典型的LASSO求解[17]问题，可以采用LASSO算法对其进行求解。

2.2 字典更新阶段

字典更新阶段，即固定稀疏表示系数A(t+1)，通过求解相应的优化函数来实现双稀疏字典D的更新。由于D=ΨΘ，且Ψ是一个事先选定好的基字典，故此阶段即为对字典结构的稀疏表示系数矩阵Θ的更新。其所求优化模型如式(18)所示：

(18)

(19)

将式(19)代入式(18)，且由于式(6)中对Θ的特殊定义，因此对矩阵Θ的更新则转变为对矩阵∑中原子的逐列更新：

(20)

Rubinstein在文献[18]中指出，可以用式(21) 来替代式(20)中的保真项：

(21)

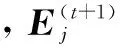
从而，式(20) 转变为如下的LASSO问题：

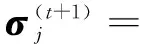
(22)

可以采用LASSO算法对其进行求解，进一步实现字典原子的更新。

2.3 D-BCS算法流程

基于前面的分析，将给出D-BCS算法的实现流程，如下所示：

输入：CS观测值Y，观测矩阵Φ，基字典Ψ，λA，λΘ，μ，τ

初始化：Σ(0)=In×n，t=0，u(0)=0，b(0)=0

Repeat

(1)稀疏编码阶段。

根据式(16)更新u(t+1)

r(t+1)=u(t+1)-b(t)

使用LASSO算法求解式(17)，获得稀疏表示系数矩阵A(t+1)

(2)字典更新阶段。

根据式(22)，利用LASSO算法逐列更新Σ(t+1)

t←t+1

Until满足停止迭代条件

3 实验及分析

选用格式为CIF的标准视频序列Foreman进行实验仿真，随机选取Foreman的第1、6、10、15、23帧作为测试样本集，如图1所示。

图1 测试图像集

实验中将大小为352×288的视频帧分成不重叠8×8的图像块，利用高斯随机矩阵对每个图像块进行观测，以获得CS观测值。设置所训练的字典原子数为256，最大迭代次数为30，λA=λΘ=0.1，μ=2.5×10-3。实验平台为ThinkPadX1Carbon3rd,Windows7,Intel(R)Core(TM)i7-5600UCPU,2.6GHz,8GB，基于MatlabR2011a编程实现。

采用传统的CS算法(稀疏基分别为DCT、K-SVD字典，重构算法选用OMP)和所提D-BCS算法对测试图像集中的每一视频帧进行重构。为了评估各算法的重构质量，除了选用PSNR作为评价标准外，近年来相关学者提出的FSIM[19]可用来衡量重构图像的视觉效果。FSIM值越高，则重构图像的视觉效果越好。实验中，为了消除随机性，每一测试帧的PSNR与FSIM值均取10次执行结果的平均值。

图2直观地给出了不同采样率下三种算法重构视频帧的PSNR和FSIM的对比情况，其中PSNR和FSIM的数值均取五幅测试帧的平均值。

图2 三种算法重构性能随采样率变化图

从图2中可以发现，随着采样率的增加，三种算法的重构性能都在提升，而所提D-BCS算法的重构性能最优。这是由于该算法在每次迭代过程中，都先进行图像估计，然后从所估计的图像中更新稀疏表示系数，进一步影响算法的重构精度。

此外，图3给出了采样率为0.375时三种算法重构出视频序列Foreman第1帧的视觉效果图。

图3从直观上进一步说明了D-BCS算法所表现的优越性。

图3 三种算法重构出视频序列Foreman第1帧的视觉效果图

4 结束语

为了解决在稀疏基先验信息未知的情况下，如何能够从压缩测量值中学习字典的同时重构出原始信号的问题，提出了一种基于双稀疏字典的新型盲压缩感知模型。实验结果表明，所提算法能很好地从压缩测量值中恢复出原始信号，且表现出更优的性能改进。

[1]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306.

[2]CandèsE,TaoT.Nearoptionalsignalrecoveryfromrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory,2006,52(12):5406-5425.

[3]DonohoDL,TsaigY.Extensionsofcompressedsensing[J].SignalProcessing,2006,86(3):549-571.

[4]AharonM,EladM,BrucksteinA.K-SVD:analgorithmfordesigningovercompletedictionariesforsparserepresentation[J].IEEETransactionsonSignalProcessing,2006,54(11):4311-4322.

[5] 练秋生,石保顺,陈书贞.字典学习模型、算法及其应用研究进展[J].自动化学报,2015,41(2):240-260.

[6]GleichmanS,EldarYC.Blindcompressedsensing[J].IEEETransactionsonInformationTheory,2011,57(10):6958-6975.

[7]AnarakiPF,HughesSM.CompressiveK-SVD[C]//Proceedingsofthe2013IEEEinternationalconferenceonacoustics,speech,andsignalprocessing.Vancouver,Canada:IEEE,2013:5469-5473.

[8]AghagolzadehM,RadhaH.Compressivedictionarylearningforimagerecovery[C]//Proceedingsofthe19thIEEEinternationalconferenceonimageprocessing.Orlando,USA:IEEE,2012:661-664.

[9]BaraniukR.Alectureoncompressivesensing[J].IEEESignalProcessingMagazine,2007,24(4):118-121.

[10]DelgadoKK,MurrayJF,RaoBD,etal.Dictionarylearningalgorithmsforsparserepresentation[J].NeuralComputation,2003,15(2):349-396.

[11]RubinsteinR,BrucksteinA,EladM.Dictionariesforsparserepresentationmodeling[J].ProceedingsoftheIEEE,2010,98(6):1045-1057.

[12] 焦李成，公茂果，王 爽，等.自然计算、机器学习与图像理解前沿[M].西安:西安电子科技大学出版社,2008.

[13]GoldsteinT,OsherS.ThesplitBregmanmethodforl1-regularizedproblems[J].SIAMJournalonImagingSciences,2009,2(2):323-343.

[14]CaiJF,OsherS,ShenZ.SplitBregmanmethodsandframebasedimagerestoration[J].SIAMJournalonMultiscaleModeling&Simulation,2009,8(2):337-369.

[15]LuK,WangQ,HeN,etal.NonlocalvariationalimagesegmentationmodelsongraphsusingtheSplitBregman[J].MultimediaSystems,2015,21(3):289-299.

[16]XiaoYH,YangJF,YuanXM.Alternatingalgorithmsfortotalvariationimagereconstructionfromrandomprojections[J].InverseProblemsandImaging,2012,6(3):547-563.

[17]TibshiraniR.Regressionshrinkageandselectionviathelasso[J].JournaloftheRoyalStatisticalSociety,2011,73(3):273-282.

[18]RubinsteinR,Zibulevsky,EladMM.Doublesparsity:learningsparsedictionariesforsparsesignalapproximation[J].IEEETransactionsonSignalProcessing,2010,58(3):1553-1564.

[19]ZhangL,ZhangL,MouX,etal.FSIM:afeaturesimilarityindexforimagequalityassessment[J].IEEETransactionsonImageProcessing,2012,20(8):2378-2386.

A Novel Blind Compressed Sensing Model Based on DoubleSparsity Dictionary

QIAN Yang,LI Lei,SHI Man-man

(Center for Visual Cognitive Computation and Its Application,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

Aiming at the problem of simultaneous image recovery and dictionary learning from Compressed Sensing (CS) measurements,where the sparse basis or the dictionary is unknown prior in the practical application of CS theory,in view of the existing Blind Compressed Sensing (BCS) theory,a novel Blind Compressed Sensing (D-BCS) algorithm based on the double sparsity dictionary has been proposed.It is an iterative method that alternates between sparse-coding and dictionary update steps.In the sparse coding stage of the proposed scheme,a split Bregman iteration based technique has been utilized to solve the non-convexl1minimizationproblemtoupdatethesparsecoefficientmatrix.Andinthedictionaryupdatestage,theoptimizationfunctionisconvertedintoaLASSO-likeproblemandthedictionaryatomsareupdatedcolumnbycolumnusingLASSOalgorithm.ComparativesimulationexperimentalresultsofseveraltestvideoframeswithavarietyofsamplingratioshavedemonstratedthattheproposedalgorithmcanrecovertheoriginalsignalfromCSmeasurementsverywellandexhibitsstate-of-the-artperformanceimprovementsinitsabilityforrecoveryofthecompressedvideoframes.

blind compressed sensing;double sparsity dictionary;split Bregman iteration;LASSO;sparse representation

2016-05-22

2016-08-30 网络出版时间：2017-03-13

国家自然科学基金资助项目(61070234，61071167，61373137，61501251)；江苏省2015年度普通高校研究生科研创新计划项目(KYZZ15_0235)；南京邮电大学引进人才科研启动基金资助项目(NY214191)

钱 阳(1991-)，女，硕士生，研究方向为非线性分析及应用；李 雷，博士，教授，研究方向为智能信号处理和非线性科学及其在通信中的应用。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170313.1545.010.html

TP

A

1673-629X(2017)05-0035-05

10.3969/j.issn.1673-629X.2017.05.008