基于尖点突变理论的液化石油气泄漏爆炸事故分析

周 扬，夏登友，高 平

●消防理论研究

基于尖点突变理论的液化石油气泄漏爆炸事故分析

周 扬a，夏登友b，高 平a

(武警学院 a.研究生队；b.消防指挥系，河北 廊坊 065000)

为完善液化石油气泄漏爆炸事故理论，提高消防部队处置此类事故的高效性和安全性，在介绍尖点突变理论原理的基础上，利用范德瓦尔热力学方程对尖点突变模型分析事故的可行性进行验证，建立了分析液化石油气泄漏爆炸事故的尖点突变模型。同时，基于尖点突变模型对事故过程进行了分析，为液化石油气泄漏爆炸事故的预防和应急处置提供理论依据。

液化石油气；泄漏爆炸；尖点突变；事故分析

0 引言

液化石油气是一种资源丰富、污染小、价格低的化工基本原料和新型燃料，被广泛地应用于工业生产和日常生活中，与此同时，其制造、运输、储存等环节暴露的问题越来越多[1]。据不完全统计，2015年全国发生燃气泄漏爆炸事故350余起，受伤712人，死亡127人，其中，天然气爆炸事故217起，死伤共计530人，液化石油气爆炸事故88起，死伤共计236人。液化石油气一旦发生爆炸，波及范围广，后果严重，不仅对周围建筑等基础设施造成毁坏，还对周边人员生命安全造成严重伤害，相关安全问题一直备受关注。针对此类事故国内学者主要从技术层面进行研究。宋文华[1]利用蒸气云爆炸模型对液化石油气储罐泄漏事故形成的蒸气云爆炸后果进行定量分析，得到相应当量的毁伤半径。邵辉[2]在试验的基础上研究液化石油气体积分数与点火能的关系以及爆炸火焰的传播过程。董影超等[3]基于事故树对液化石油气沸腾液体扩展蒸气爆炸进行研究，确定了事故发生模式和事故控制模式。黄金印等[4]基于“能量意外释放理论”和“两类危险源理论”对液化石油气泄漏爆炸事故的发生机理进行分析。以上研究对液化石油气泄漏爆炸事故进行了有益的探索，然而，液化石油气泄漏爆炸事故是一个复杂系统，不确定因素较多，仅靠技术等层面研究复杂系统问题还是存在一定的缺陷。因此，为深入研究液化石油气泄漏爆炸事故机理，还需从复杂系统的角度研究事故更深层次的机理。

液化石油气泄漏爆炸的发生机理遵循着内在规律，根据拓扑学、群论等原理建立的事故灾害的突变理论，可以为消防部队在液化石油气泄漏事故处置分析中提供一种灾变模型。目前，应用突变理论对此类事故的分析还处于探索阶段。袁晓芳[5]针对工业事故的突变特点和传统系统评价预警方法的弊端，介绍突变理论评价预警的原理，提出了工业事故突变预警的方法。魏伟[6]根据建筑突发事件的特点，提出了利用突变理论描述建筑突发事件，并将研究结果用于辅助处理突发事件决策。目前，还没有将突变理论用于液化石油气泄漏爆炸事故分析中。本文运用尖点突变模型描述液化石油气泄漏爆炸过程，将影响液化石油气爆炸事故的因素归结为系统的液化石油气浓度和以点火源为主要特征量的不确定因素两个控制变量，得到液化石油气泄漏爆炸灾变流形，可用于液化石油气泄漏事故的预防和应急处置。

1 突变理论原理

突变理论是由法国数学家托姆在20世纪70年代发展起来的一个新的数学分支[3]。突变理论以不连续现象为研究对象，运用拓扑学、奇点理论和稳定性等数学工具，以系统结构稳定性为基本出发点，认为突变现象的本质是系统或过程从一种稳定状态向另一种稳定状态的跃迁。

突变理论用一组参数描述系统所处的状态，即用状态空间中的点表示每一个运动状态。当系统处于稳定状态时，表明该系统状态的某个函数取一定的值。当参数在某个范围内变化时，系统从一种稳定状态进入不稳定状态，而参数略作变化，将使处于不稳定状态的系统进入另一种状态，从而状态发生了突变。突变现象是一种由量变向质变的飞跃，揭示事物质变方式是如何依赖条件变化的[6]。突变理论的基本特点是根据一个系统的势函数将系统的临界点分类，研究分类临界点附近状态的变化特征，从而归纳出若干个初等突变模型，并以此来探索某些事故中的突变现象。

对于突变模型中的势函数V(x)，它所有的临界点集合成一平衡曲面。通过对V(x)求一阶导数，并令DV(x)=0，即可得到其突变流形。通过势函数的二阶导数D2V(x)=0求得该平衡曲面的奇点集。由DV(x)=0和D2V(x)=0可得由状态变量表示的反映状态变量与各控制变量之间关系的分解形式的分歧方程[6]。七种初等突变模型如表1所示。

表1 七种初等突变模型

为准确分析液化石油气泄漏爆炸事故的机理，本文应用突变理论中的尖点突变模型。尖点突变是灾变理论中应用最广的，它具有两个控制变量u、v和一个状态变量x，其势函数表示如下：

其中，u=fu(u1,u2,…，un)，v=fv(v1,v2,…，vn)。

该势函数组成了一个三维空间。平衡曲面M由对势函数求一阶导数确定，即DV(x)=0：

对尖点突变的势函数V(x)=x4+ux2+vx求二阶导数，计算奇点集方程，即D2V(x)=0：

将式(2)和(3)联立消去状态变量x，得到分歧点集：

其相空间是一个三维空间中的具有褶皱的光滑曲面，如图1所示。该曲面可分为上叶、中叶、下叶，它们代表了三种不同的平衡位置，上叶、下叶是稳定的，中叶是不稳定的[5]。当u取正值时，如果一个相点从平衡曲面的上叶移动到下叶或从下叶移动到上叶，u和v的平稳变化几乎总是引起x的平稳变化。但当u取负值，参数u和v满足式(4)时，相点恰好在曲面折回的边缘上(曲面折回而形成的中叶处)，它必定由上叶跳跃到下叶上或从下叶跳跃到上叶上，这即引起了参数x的突跳。本文将状态变量x和控制变量u、v的取值范围限定在-1～1之间[7]，曲面折回的边缘在控制变量平面上的投影就构成了分叉集，它是可能使x发生跳跃突变的控制变量的集合。

图1 尖点突变模型

2 尖点突变模型的数学分析

为验证尖点突变模型可用于分析液化石油气泄漏爆炸事故，现对尖点突变模型进行数学分析。液化石油气泄漏的浓度u与泄漏的部位、周围环境、处置措施等有关，引起液化石油气/空气混合气体燃烧爆炸的另一个重要因素为系统的点火源，它受诸多因素的影响，如静电火花、电火花、明火等，把这些不确定因素集记为v。尖点模型势函数为：

分析系统状态的变化趋势，目的是判断它是否越过了相应于灾变流形的分叉点，从而确定系统安全状态的形变。从能量因素和不确定因素两个方面入手进行分析，式(5)中，等号左边隐含了系统的安全状态，右边是系统控制变量及其对安全的影响程度。由于液化石油气泄漏爆炸是发生在气相的灾变事故，系统状态可以用气体密度ρ来表示，控制变量用泄漏的液化石油气分压P及温度T来表示。对于液化石油气/空气混合气体系统，其状态函数为f=f(ρ,P,T)，一般气体的状态变化遵循范德瓦尔热力学方程[8]：

式中，a，b表示影响系统3个参量的扰动因子；R为气体常数；c为比热，c=1/ρ。

当系统处于稳定状态时，df/dρ=0，则有f=f(ρ,PC，TC),PC、TC是定值。当系统处于非稳定状态时，∂f/∂P=∂f/∂ρ，由范德瓦尔热力学方程变形得：

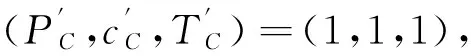
因为ρ′=1/c′，故令P=P′-1,ρ=ρ′-1,T=T′-1，于是可以得到：

令u=8T+P/3,v=8T-2P/3，则

式(11)表明，范德瓦尔热力学方程和尖点突变模型势函数具有相同的拓扑结构，故尖点突变模型可以运用于液化石油气泄漏爆炸事故的分析中。用空气密度ρ代替x，表示液化石油气泄漏时系统的状态；液化石油气的气体分压P和温度T表征了系统控制变量u和v。

表征液化石油气泄漏爆炸灾变曲线的流形是∂f/∂ρ=ρ3+uρ+v=0,即尖点突变曲面投影投射到平面上的分叉线，防止液化石油气爆炸过程控制的重点是该流形的分叉点。

3 应用分析

液化石油气的浓度与空气中的氧浓度存在一定的关系，即液化石油气浓度增大，空气中的氧浓度将减少，可以用函数式表达清楚。所以，控制液化石油气泄漏爆炸的参数可简化为液化石油气气体浓度u和点火能，由于产生点火能的条件复杂，所以可以称其为不确定参数v。确定反映系统安全状态的参数x，就可以得到系统的尖点突变模型，如图2所示。

图2 液化石油气泄漏爆炸的尖点模型

3.1 爆炸过程分析

图2的曲面是尖点突变的流形，曲面折叠部分代表了发生液化石油气泄漏爆炸的灾变区域，该区域将系统的安全状态分成了上、中、下三个部分，曲面的上叶表明系统较为安全、稳定，事故没有发生；下叶表示系统的功能状态差，爆炸事故随时可能发生；中叶表示系统的功能状态发生突跳，即为发生泄漏爆炸事故。

曲线abcd表明了液化石油气泄漏爆炸的全过程。其中，ab是泄漏的液化石油气积聚的过程，液化石油气中的各可燃气体分子与氧分子的化学活性不断增强，分子之间的碰撞增强，不断产生活性氧自由基和氢自由基[9]。当液化石油气浓度达到F(a)时，整个系统处于液化石油气的爆炸极限范围内。到达临界点b时，若未采取任何应急处置措施改善外界条件，液化石油气不断积聚使系统的安全状态不断向不利的方向发展，当不确定因素导致的点火能F(v)产生，系统的安全状态变量x由b点突跳至h点，链式反应被激发，反映为曲线abh，表现为泄漏的液化石油气发生燃烧爆炸。由于反应是放热的，产生的热量不能立即在系统中传递或损失掉，系统就会出现瞬间热量的累积，使系统的温度上升，从而加速化学反应，进一步释放大量的热量，造成热量失衡，从而引起热爆炸，即为曲线的cd段。

3.2 爆炸规模分析

图2中三条不同的曲线，分别表示在泄漏的气体浓度因素和点火能的不确定因素作用下系统状态所发生的变化过程。当点火能的不确定因素v和气体泄漏浓度u同时恶化时，就有可能使系统的功能状态x产生恶化，曲线abcd的b→h表示系统发生了突跳，即发生爆炸事故，其变化值为Δx1=x(vb,ub)-x(vh,uh)，相应地在分叉集上便是一条经过分叉点集两个边缘的曲线，如图3所示。事故恶化程度x的大小取决于v和u的危险程度，曲线jkmn在k→l发生突跳时的突跳大小为Δx2=x(vk,uk)-x(vl,ul)，Δx1<Δx2，表明前者为小型爆炸事故，后者相对于前者则为规模较大的爆炸事故。反映在图3分叉集上，则为两条跨越分叉集边缘线程度不同的曲线afbd和jrkn。曲线pq表明，当突变流形上曲线从上叶向下叶发展时，如果不经过折叠线，也会导致系统的安全状态x恶化，但不会导致爆炸事故的发生。

3.3 爆炸预防和处置分析

防止液化石油气泄漏爆炸事故，即防止泄漏的液化石油气的状态越过液化石油气爆炸的突变分叉集。当点火源等不确定因素v和泄漏的浓度u处于极度不安全的状态时，只关注稀释泄漏的液化石油气浓度，而不重视消除点火源等不确定因素，非但起不到预防事故、提高系统安全状态的作用，相反容易导致爆炸事故的发生。所以预防爆炸事故发生，消除点火源等不确定因素是决定性手段，稀释泄漏的液化石油气浓度是重要手段，以使处置过程曲线避开折叠线，在不发生爆炸事故的前提下提高系统的安全性。

图3 液化石油气泄漏爆炸尖点突变的分叉集

液化石油气泄漏爆炸事故应急处置常用方法有关阀断气、消除火源、喷雾稀释等，其过程表现为defa。液化石油气泄漏燃烧爆炸过程中，通过一定的处置措施使系统的控制变量v变小，即控制点火源等不确定因素的产生，系统状态由e点突跳到f点，即熄火现象[10]。燃烧爆炸系统不仅具有突跳性、多态性，而且还具有滞后性，即在液化石油气燃烧爆炸的灭火阶段，采取措施控制系统的热效应后(dc段)，当系统到达c点时并不产生突跳，而是状态到达e点时才产生突跳。因此，液化石油气一旦发生爆炸，输入的能量必须大于火灾形成时的扰动能量，才能使火灾熄灭。

当泄漏现场的液化石油气浓度在爆炸极限范围内，而且现场情况不确定因素较多，即事故系统处于中叶，系统无论朝哪个方向都会发生突变。此时，现场指挥员要根据事故系统所处的实际情况决定处置措施，使系统发生突变或者缓解。若周围的环境允许事故系统发生突变，现场指挥员应果断地采取措施使系统状态向上叶或下叶发展；当周围环境不允许发生突变时，应采取相应的措施缓解现场的险情，控制系统发生突变。

4 结论

4.1 通过数学分析，范德瓦尔热力学方程和尖点突变模型势函数具有相同的拓扑结构，利用尖点突变理论来分析液化石油气泄漏爆炸事故是可行的。

4.2 为避免液化石油气泄漏爆炸，可采取以下措施：泄漏的气体浓度在爆炸极限范围内时，禁绝现场环境点火源等不确定因素；周围点火源等不确定因素较多时，将泄漏的液化石油气浓度时刻控制在爆炸极限范围外。

4.3 当系统处于爆炸的危险状态时，要避免事故的发生，曲线不能跨越分叉集。在事故处置中，稀释泄漏气体浓度的同时，重点要对点火源等不确定因素进行消除，否则易导致爆炸事故的发生。

[1] 宋文华,董颖超,谢飞.液化石油气储罐泄漏发生爆炸事故的后果分析[J].南开大学学报(自然科学版),2012,45(1):106-111.

[2] 邵辉,段国宁,邵峰,等.液化石油气点火能试验及爆炸火焰传播分析[J].中国安全科学学报,2011,21(8):54-60.

[3] 董影超,宋文华,谢飞.液化石油气发生沸腾液体扩展蒸气爆炸的事故分析[J].南开大学学报(自然科学版),2012,45(1):95-105.

[4] 黄金印,姜连瑞,夏登友,等.公路气体罐车泄漏事故应急处置技术[M].北京:化学工业出版社,2014:26-27.

[5] 袁晓芳,李红霞,田水承.突变理论在工业事故预警中的应用[J].西安科技大学学报,2011,31(4):482-488.

[5] 魏伟,余庄.基于突变论的建筑突发事件研究[J].安全与环境学报,2009,9(1):144-147.

[6] 周荣义,黎忠文,牛会永.基于突变理论的油库火灾爆炸分析与模糊动态评价[J].中国安全科学学报,2006,16(6):97-101.

[7] 李建行,夏登友,武旭鹏.非常规突发事故的演化机理与演变路径分析[J].安全与环境工程,2014,21(6):166-170.

[8] QIN X,QIAO G.Cups model for risk analysis[J].Journal of Beijing Institute of Technology,1998,8(2):219-223.

[9] 李思琦,李刚,季庭超.某槽罐车爆炸事故原因及救援措施分析[J].工业安全与环保,2015,41(1):73-76.

[10] 吴松林,杜扬.基于突变理论的国内外火灾科学研究进展和展望[J].火灾科学,2013,22(2):59-64.

(责任编辑 马 龙)

Cusp Catastrophe Theory-based Analysis of LPG Explosions Caused by Leakage

ZHOU Yanga，XIA Dengyoub，GAO Pinga

(a.TeamofGraduateStudents;b.DepartmentofFireCommanding,TheArmedPoliceAcademy,Langfang,HebeiProvince065000,China)

To perfect the theory of LPG explosions and improve the efficiency of firefighting department’s accident disposal, this paper introduces the catastrophe theory briefly and verifies the feasibility of the cusp catastrophe model with Van der Waals’s equation. Then the paper analyses the process of the accidents with the cusp catastrophe model and provides scientific and theoretical basis for the prevention and disposal of LPG explosions caused by leakage.

LPG; explosion caused by leakage; cusp catastrophe model; accident analysis

2016-12-28

周扬(1992— )，男，山东荣成人，军队指挥学在读硕士研究生； 夏登友(1973— )，男，安徽庐江人，副教授； 高平(1993— )，男，甘肃白银人，军队指挥学在读硕士研究生。

X931;D631.6

A

1008-2077(2017)04-0005-05