小规模突发事件疏散模型的改进与分析*

郑友亮

（广东省科技基础条件平台中心）

小规模突发事件疏散模型的改进与分析*

郑友亮

（广东省科技基础条件平台中心）

针对小规模城市突发事件疏散问题，现有模型忽略交通状态的影响，与实际疏散过程不相符。引入路径时间估计方法对突发事件疏散模型进行优化：首先利用马尔科夫路径原理计算相邻路段交通状态发生的概率；然后估计相邻路段行程时间；最后经过扩展实现对整个路径时间的评估。仿真结果表明，改进后的模型能满足小规模突发事件的需求。

突发事件；应急疏散；马尔科夫路径；行程时间估计

0 引言

突发事件是一种发生规模不确定的紧急事件，可能对社会造成严重危害。应急部门要在最短时间内疏散危险区域内无主动疏散能力的人员来降低损失，同时需考虑疏散成本。对于疏散问题，文献[1]基于路径网络流控制建立了疏散模型，并验证策略的有效性，具有一定的实际意义；文献[2]研究大型路网情况下突发灾难人员疏散问题，建立了模型并进行仿真，但该模型主要针对大型事件；文献[3]建立了蚁群算法疏散模型，研究最短疏散路径，但该算法运算复杂度高，较为耗时；文献[4]建立分层的疏散模型，借助引导者降低事故损失，文中缺乏非典型疏散行为的分析，具有一定的局限性；文献[5]建立了较为完善的应急疏散模型，但未考虑道路的交通情况，并不符合实际疏散情况；文献[6]将行程分为3部分因素进行评估，求最短行驶路径，未将车流量、路段长度考虑在内，适用范围受到限制；文献[7]根据交通状况概率评估行程时间，取得较高的估计精度，可为行程时间估计提供理论参考。

目前，疏散模型是在较为理想条件下创建的，缺少交通状况[8]的影响，与实际疏散过程不同，实用性较低。为此，本文引入交通路径行程时间估计方法，实现对总路段数小于30[5]的小规模疏散模型的改进，使数学模型更接近实际情况，并以疏散过程中产生的成本为目标进行优化。

1 问题描述与数学模型

1.1 问题描述

应急疏散[9]问题通过如下案例说明：某服装场发生火灾事故，应急部门需要快速将伤员送到医院。疏散过程中的其他因素导致伤员数量增加，伤员数量不确定。应急疏散车辆必须与应急中心保持联系，及时根据现场的情况进行调度。另外应急车辆可能在行驶路径上接收其他伤员，因此会多次停靠。疏散过程可以归结为：应急车辆搭载的伤员数量有限；运输路径上并不是所有节点都要停靠，疏散过程用图1表示。

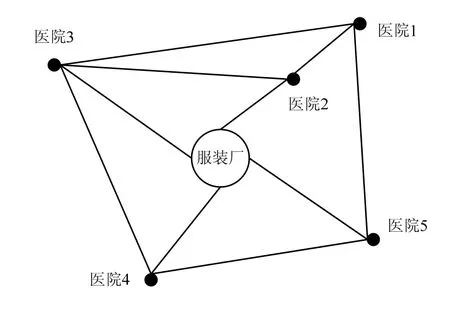
图1 应急疏散图

1.2 数学模型

数学建模需满足以下条件：1)仅疏散伤员，不分受伤程度；2)应急车辆承载量相同，每辆可搭载M名伤员，一名伤员的运输成本为C，成本随时间变化函数为每辆车在某节点的停留次数，含义为t时间段应急车辆v在节点（i，j）停留次数；4)应急车辆停滞时的成本为 Cs；5)疏散成本为优化目标。

成本因素主要有：1)每个时段应急车辆在节点的停留成本；2)每个时段从危险点和其他节点运送伤员到医院的成本；3)每个时段滞留在危险点和其他节点上的伤员成本。模型的目标函数为

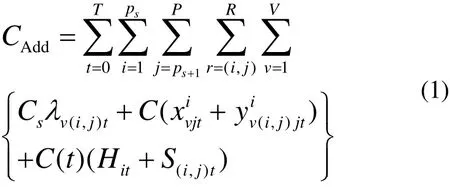
2 路径时间估计

应急疏散过程中交通状况影响疏散速度，路径越长损失越大，增加疏散成本。为此，估计疏散行程时间[10]，并作为成本影响因素引入到疏散模型。

疏散过程中应急车辆经过的每一段路径其状态分为畅通和堵塞，模型为

2.1 相邻路段概率计算

每个路段的状态仅有2种：畅通与堵塞，相应的路段状态概率函数可以表示为

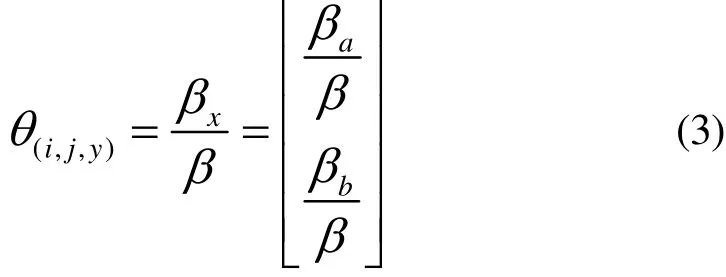
对于同一路径上的2个相邻路段，总的路况可延伸为

2.2 相邻路段行程时间估计

根据马尔科夫路径模型[7]，对相邻路段行程时间进行估计，设路段的行程时间为Td，其中d代表路段状态种类，相邻的2个路段有4种情况，故相邻的2个路段的行程时间可以评估为

其中，qd表示路况发生的概率；表示相邻两路段的时间估计。由式(5)可知相邻路段的行程时间估计是以路况发生的概率为权重，求路径行程时间的加权平均值。

2.3 路段行程时间的拓展

在实际疏散过程中，每条路径所包含的路段不止2个。若设某条疏散路径上有l个路段，则由式(4)可形成l-1个二维状态概率矩阵。同理根据相邻路径概率计算方法可得多段相邻路径概率计算公式为

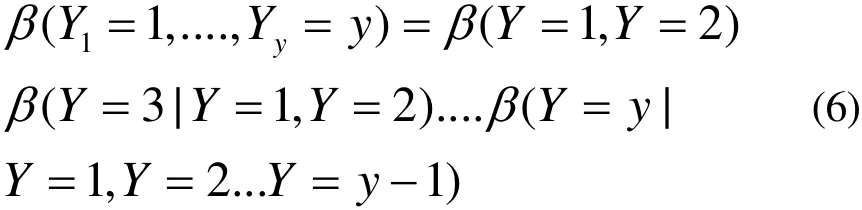
3 模型改进

结合实际疏散过程，交通状态是不可忽视的影响因素，将行程时间作为第4个成本因素引入疏散模型，增强模型的实用性。设应急车辆行程时间成本与时间比例系数为CT，将式(7)乘以CT转化为时间成本引入式(1)则优化后的目标函数为

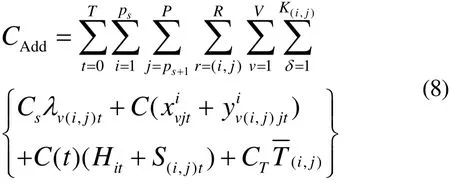
其中 CAdd为总成本，是模型的优化目标。

该模型的约束条件有以下3点：

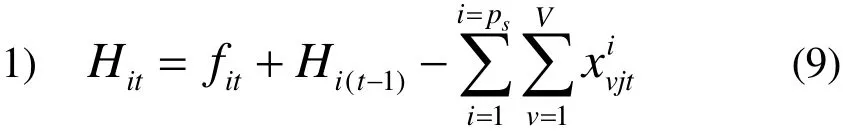
其中，fit为时刻t危险点i新增的伤员数量；Hit为时刻t危险点i上的伤员数量；

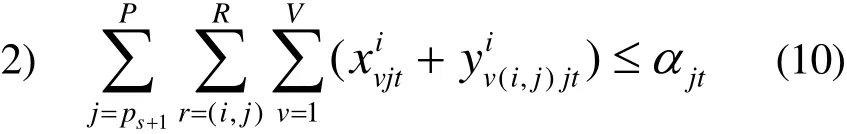
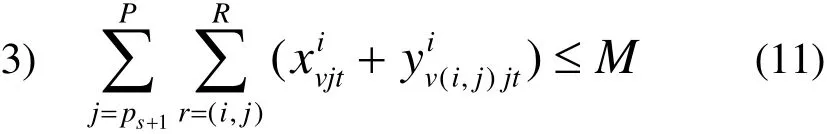
其中，t时间段应急车辆接收的伤员数量应小于车辆的承载量，变量均为整数，单位为分钟。

4 求解、仿真与分析

4.1 模型求解

本模型中影响成本的关键因素主要有目标函数和约束条件中的变量，如表1所示。模型变量个数为I*V*T+J*V*T+I*T+I*J*T+J*T+K*I*J；约束条件为I*V*T+I*J*V*T+I*J*T+I*J*V*T+I*J*T，综上可知，模型的决定因素可简化为即4级方程，可解性非常大。

表1 模型的变量和约束条件

4.2 仿真分析

为验证模型的有效性，结合实际案例进行仿真。仿真使用的计算机为Intel(R)Core(TM)CPU 2.5GHz，4 GB内存的64位操作系统，仿真软件为ILOG CPLEX。

以某石化公司气体泄漏事故为例进行模拟实验，发生时间为上午8点，疏散范围包含该厂附近的2个区域。案例如图2所示，包括3个危险点；3个安全点（医院）；9条有效路径（从危险点到安全点），每条有效路径由3～6个路段组成；并且设定救援时段为6，每个时段15分钟；应急中心调动15辆救护车，每辆车可承载6名伤员；每个伤员的疏散成本为400元；救护车停靠一次成本为3800元；每辆救护车1分钟行程时间的成本为1000元；本次事故造成约190万元的经济损失，疏散不同程度伤员约250人。

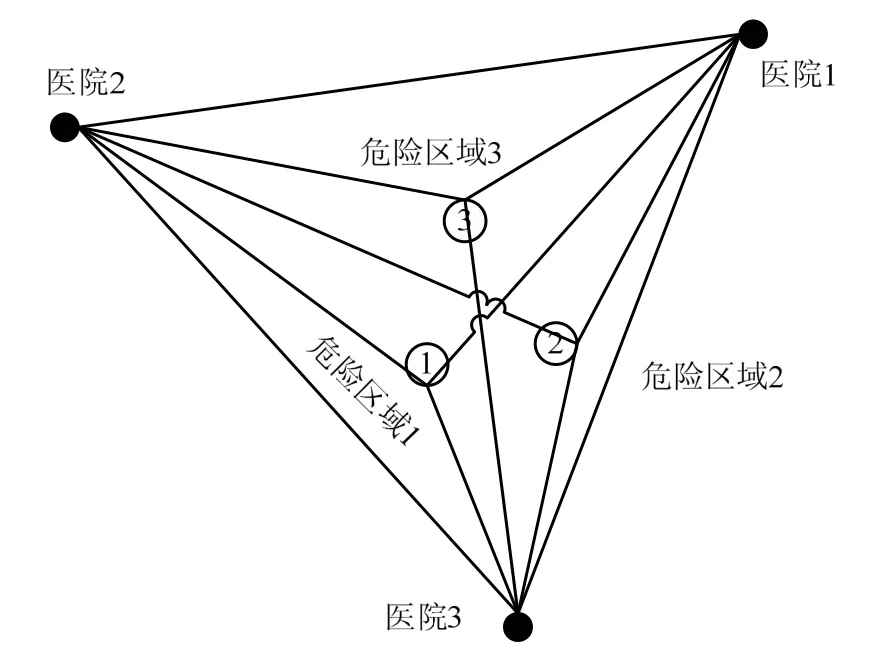
图2 案例模型图

以上所述，数据为实验所输入的应急现场参数，利用ILOGCPLEX软件进行仿真。统计每个时段救护车在安全点停留的班次/疏散伤员人数、每个时段滞留在危险点的伤员人数、应急车辆的疏散路径数以及路径时间分别如表2、表3、表4所示。

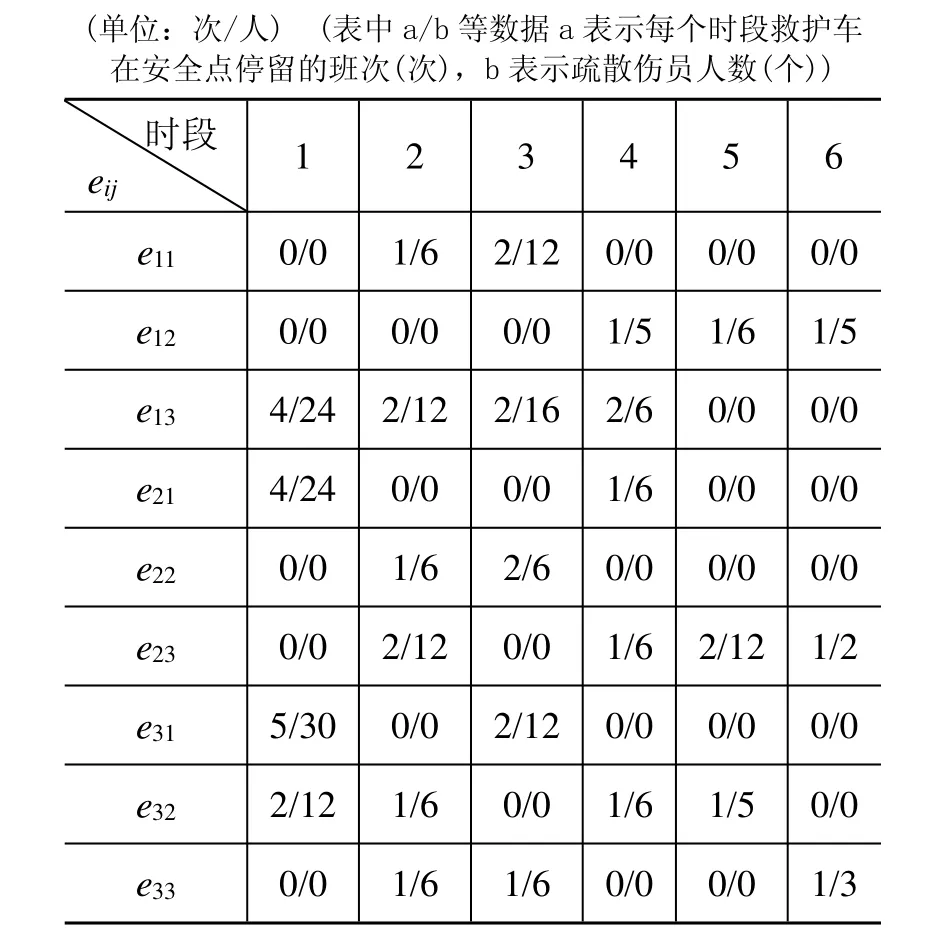
表2 救护车在安全点停留的班次和疏散的伤员人数

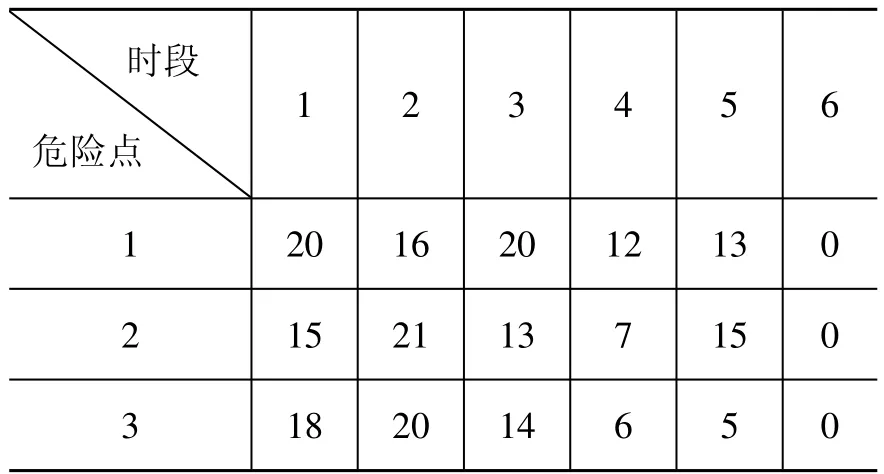
表3 滞留在危险点的伤员人数 （单位：人）

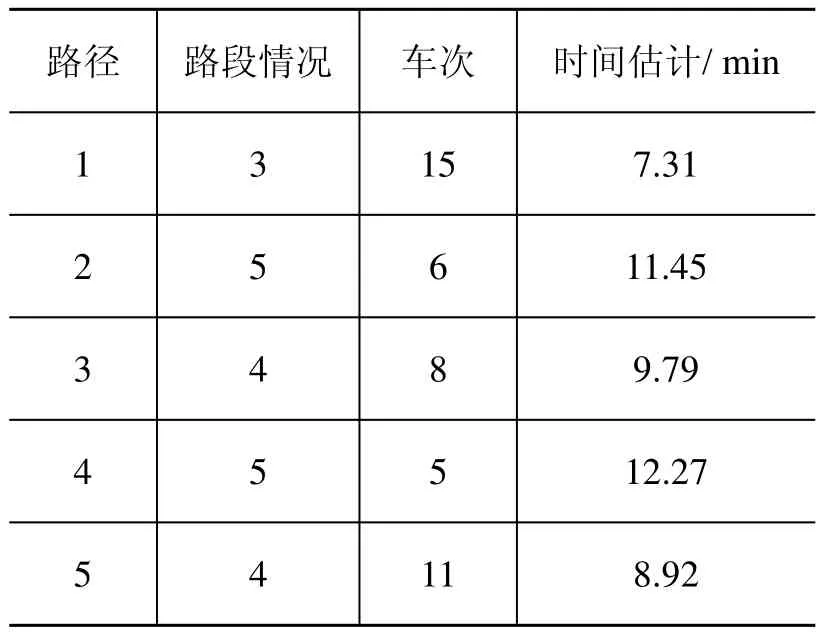
表4 路径时间估计

在以上6个时段内，应急中心根据现场伤员情况，结合物联网提供的实时救护车资源状况进行了26次任务调度，初次调度时救护车全部处在空载状态，应急中心根据3个危险点的伤员数量分别向危险点1派送4辆、向危险点2派送4辆、向危险点3派送7辆救护车，救护车满载输送伤员。从时段2开始，应急中心根据物联网反馈的救护车状态进行实时调度。当前时段来不及疏散的伤员同下时段产生的新伤员被认为是滞留人员，等待下次调度进行疏散。疏散过程中应急车辆选择了5条疏散路径，每个路径的路段情况和路径时间估计如表4所示。

仿真实验的运算时间为1023ms，各部分影响因素产生的成本和本次突发事件疏散过程中的最优成本如表5所示。对比最优成本更接近实际经济损失，而不考虑影响因素实际行程时间时的成本为629782.7元，与实际成本相差较多。

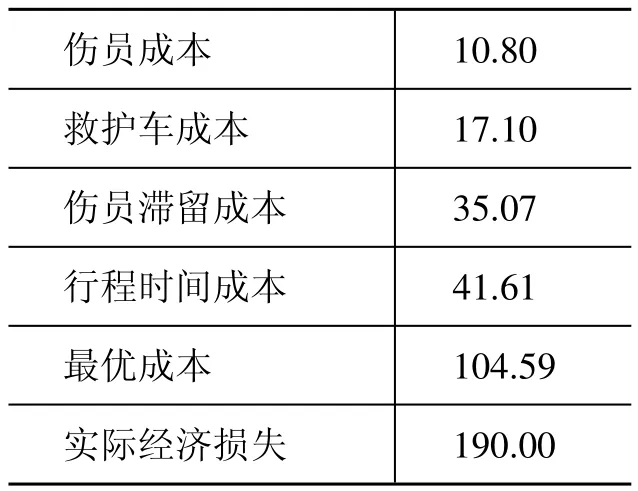
表5 事件成本 （单位：万元）

本案例属小规模疏散（路段数为21，小于30），为验证其有效性，设计了如下2个规模按0.5比例系数增大的对比试验。试验一，按比例系数增大有效疏散路径，即增加新的安全点，新路径所产生的伤员数量保持与原有路径相同；试验二，保持危险点和安全点不变，等比例增加每个时段危险点的伤员数量。通过仿真观察系统的求解时间分别如图3和图4所示。

分析图3可知，当突发事件的疏散路径数不大于27时，模型的求解时间曲线接近线性，斜率变化较小，小规模突发事件对求解时间的影响比较平缓。分析图4可知，随着受伤人数的等比例增加，在受伤人数少于607时模型求解时间的变化率非常接近，变化并不明显，随着突发事件规模的增大模型的求解时间等比增加。故此改进后的模型在应对小规模突发事件时更有效。

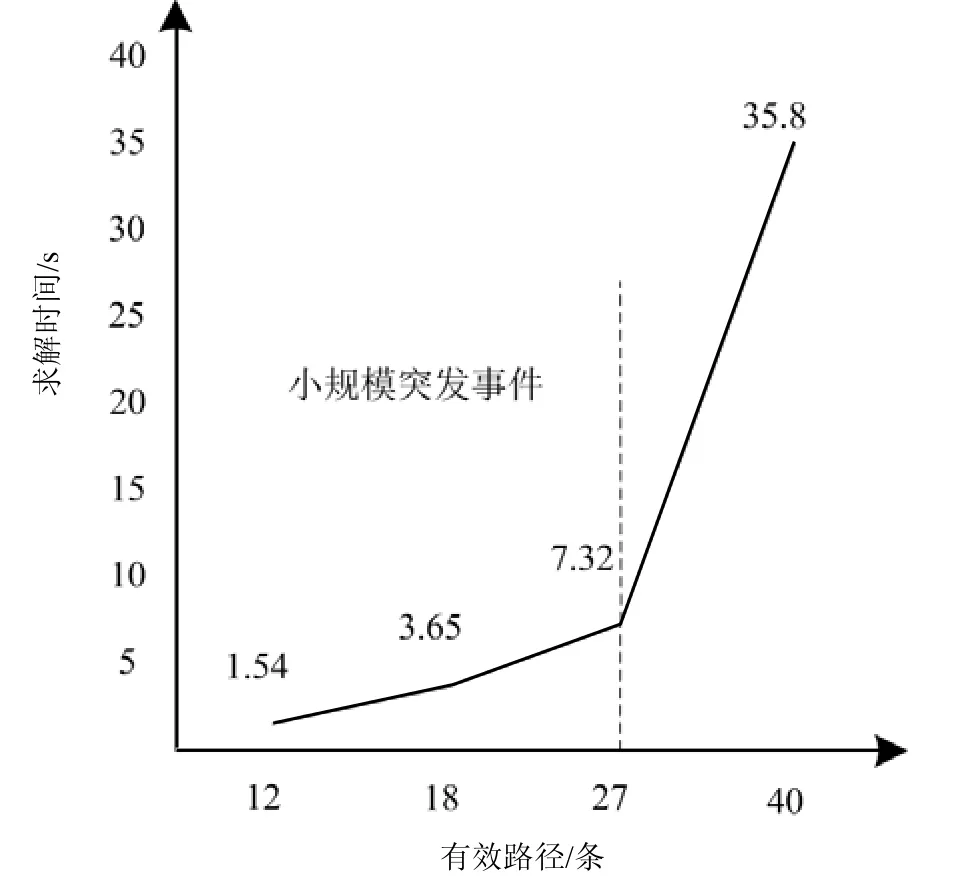
图3 有效路径对模型求解时间的影响

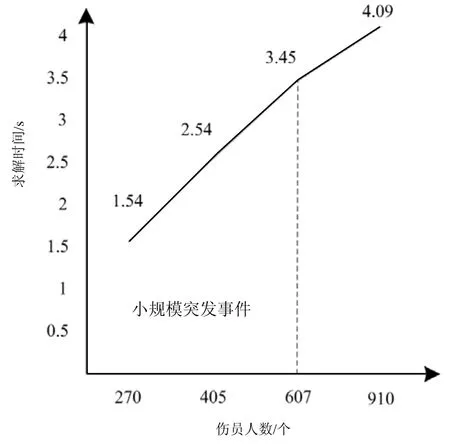
图4 受伤人员数量对模型求解时间的影响

5 结论

结合实际疏散情况引入路径时间影响因素，改进了疏散模型。试验结果表明原模型的优化成本为629782.7元，改进后模型的优化成本为1045922.7元，更接近实际疏散产生的成本，误差为8.1%，表明本模型在小规模事件中具有较好的实效性。

[1]李进,张江华.基于路径的网络流控制应急疏散模型与算法[J].自然灾害学报,2012,21(6):9-18.

[2]赵岩,高社生,姜微微.突发灾难下大型路网中的人员疏散模型[J].长安大学学报(自然科学版),2013,33(2):89-94.

[3]杨敬,石明全,韩震峰,等.一种蚁群算法疏散模型优化的方法[J].消防科学与技术,2015,34(3):343-345.

[4]魏心泉,王坚.基于熵的火灾场景介观人群疏散模型[J].系统工程理论与实践,2015,35(10):2473-2483.

[5]牛金山,刘晓.基于物联网技术的实时应急疏散调度研究[J].中国安全科学学报,2011,21(9):166-171.

[6]姚丽亚,关宏志,魏连雨,等.基于实时交通信息的行程时间估算及路径选择分析[J].公路交通科技,2006,23(11):86-89.

[7]张俊婷,周晶,徐红利,等.基于空间型马尔科夫链的行程时间估计模型[J].系统工程,2015,33(12):72-77.

[8]刘丽霞,杨骅飞.突发事件等复杂情形下的交通路径选择问题[J].北京联合大学学报(自然科学版),2004,18(3):67-71.

[9]孙绪彬,董海荣,宁滨,等.基于ACP方法的应急疏散系统研究[J].自动化学报,2014,40(1):16-23.

[10]胡彬,王冰,王春香,等.一种基于时间窗的自动导引车动态路径规划方法[J].上海交通大学学报,2012,46(6):967-971.

Im provementand Analysisof Evacuation M odel for SmallScale Emergency

Zheng Youliang
(Guangdong Science&Technology Infrastructure)

Considering the problem of small scale urban emergency evacuation,the existingmodels ignore the influenceof traffic state,which isnotconsistentw ith the actualprocess.To thisend,thispaper introducespath time estimationmethod to optim ize themodel of emergency evacuation.Firstly,the probability of traffic flow in adjacent sections is calculated by Markov path principle,and the travel time of adjacent sections is estimated. Finally,the travel time of the whole path was evaluated by Mathematics prolongation.The results show that the improvedmodelhasmore practicalsignificance,and themodelcanmeet the needsof smallscaleemergencies.

Emergency;Emergency Evacuation;Markov Path;Travel Time Estimation

郑友亮，男，1985年生，本科，工程师，主要研究方向：计算机技术及应用、科技项目管理。Y lzheng2008@qq.com

广东省科技计划项目（2014A020219001，2016A020224002）