S变换在配网故障行波信号分析中的算法研究
2017-06-02吴阳阳舒勤
吴阳阳 舒勤


摘要:分析了S变换的一些特性,探讨了S变换在配网故障定位中的应用及其优势,对比了其他传统的配网故障数据处理方式,指出S变换应用于配网故障行波数据分析的优势。针对零模和线模电压行波受频散效应、混叠效应等各种因素影响畸变严重、上升沿缓慢难以读取而且后续折反射波信息无法利用的问题,利用S变换对非平稳信号的的分频段呈现作用,读取波形极值即可对初始波头以及后续若干波头进行精确标定,从而提高了配网行波法故障定位的精度。在PSCAD及Matlab仿真中验证了本方法的有效性和准确性。
关键词:S变换;配电网;故障测距;频散效应
中图分类号:TM711 文献标识码:A 文章编号:1007-9416(2017)04-0135-03
中国配电网的中性点运行方式绝大多数多为小电流接地运行方式,在该方式下馈线发生单相接地故障时,系统仍可持续运行1~2h,这极大地提高了供电的连续性,但这种方式同时的故障电流会很小,难以识别,给故障点的定位带来了一定挑战。及时准确地判断故障位置对于防止故障进一步扩大、提高供电可靠性具有重要意义。
行波法是电力故障测距的常用有效方法。现有的比较成熟的电网故障定位方法基本上都是针对高压输电网的。但配电网结构往往比较复杂,存在多级分支、环网、线路距离短等问题,这些都给配电网故障测距增加了难度。常规的故障测距方法使用三相电压的零模和线模数据,但是这些数据误差较大,在复杂的行波折反射背景下、以及行波衰减与色散的影响下精度严重下降。近年来兴起的S变换理论,因其本身的一些特性,将其引入配网故障行波数据的处理中,可以有效提高定位精度。仿真实验证明了该方法精确性和有效性。
1 S变换理论
S变换最早由地球物理学家R.G.Stockwell于1996年提出,是一种可逆的加窗傅氏变换时频分析方法,或者说是以Morlet小波为基本小波的连续小波变换的延伸。其本质上是加归一化高斯窗的短时傅里叶变换或经过相位校正的小波变换。对信号的变换定义式如式(1)。该变换继承了短时傅变和小波变换的局部化思想,但不同于短时傅变的窗函数高度宽度固定、小波变换的母小波只可在固定位置伸缩且母小波受零均值约束,S变换的窗函数的高度、宽度是随频率变化的。因此在具有短时傅变和小波变换优点的基础之上,同时具有了较高的频率分辨率和时间分辨率。
2 S变换的性质
2.1 局部性
即可得到信号的频谱,即S变化的结果沿时间轴平均后就等效于信号的时间局部傅里叶频谱,而且可以通过式(4)方便地恢复信号。这就说明S变换是非平稳时间序列的广义傅氏变换。
2.2 线性
S变换是时间序列的线性运算。S变换可不受交叉项影响,提高了联合时频域中的分辨率。
2.3 无损可逆性
由式(3)和(4)可知,S变换类似傅氏变换,既可以从时间域变换到时频域,也可以通过反变换从时频域变回到时间域,整个过程并无信息丢失,即具有无损可逆性。
2.4 多分辨率
在S变换的定义式中,等同于小波变换的尺度因子,频率低时,时窗宽,尺度大;频率高时,时窗窄,尺度小,因此具有多分辨率特点。某种意义上可以认为S变换可以将信号分频段呈现,而这一性质是本文重点关注的性质。
待处理信号经S变换后,生成一个行列的二维复矩阵。求模后即得到所需要的S矩阵。
得到的S矩阵行向量对应信号在特定频点处的幅值随时间的变化。可以类比于小波变换不同尺度下的处理结果。列值对应时域坐标,行值对应不同频率段,原始信号的0到最高频率fn线性映射到1~上。
可见S变换的一大特征就是可以分频段呈现原始数据,而影响故障行波信息提取的主要因素就是行波的衰减和色散,这两个原因都和频率相关,如果我们能在特定频段处分析行波信号,则可以有效避免行波衰减和色散带来的影响,从而提高信息提取精度,给行波法故障定位带来精度上的提升。
3 S变换应用于配网故障定位的优势分析
行波法测距核心是依靠测量波头到达时刻来计算故障距离,因此准确提取波头信息以及后续行波信息对于配网故障定位有重要意义。本节就S变换相比常用的零模数据或者线模数据的优势做详细分析。
以如图1所示线路发生故障为例,故障点为e2处(图中相应小写字母代表对应线路,冒号后数字为线路长度,图中闪电折线表示单相接地故障位置,e2代表故障位置在e线路上距M端2Km处,图中闪电折线标注的即是这个位置。)
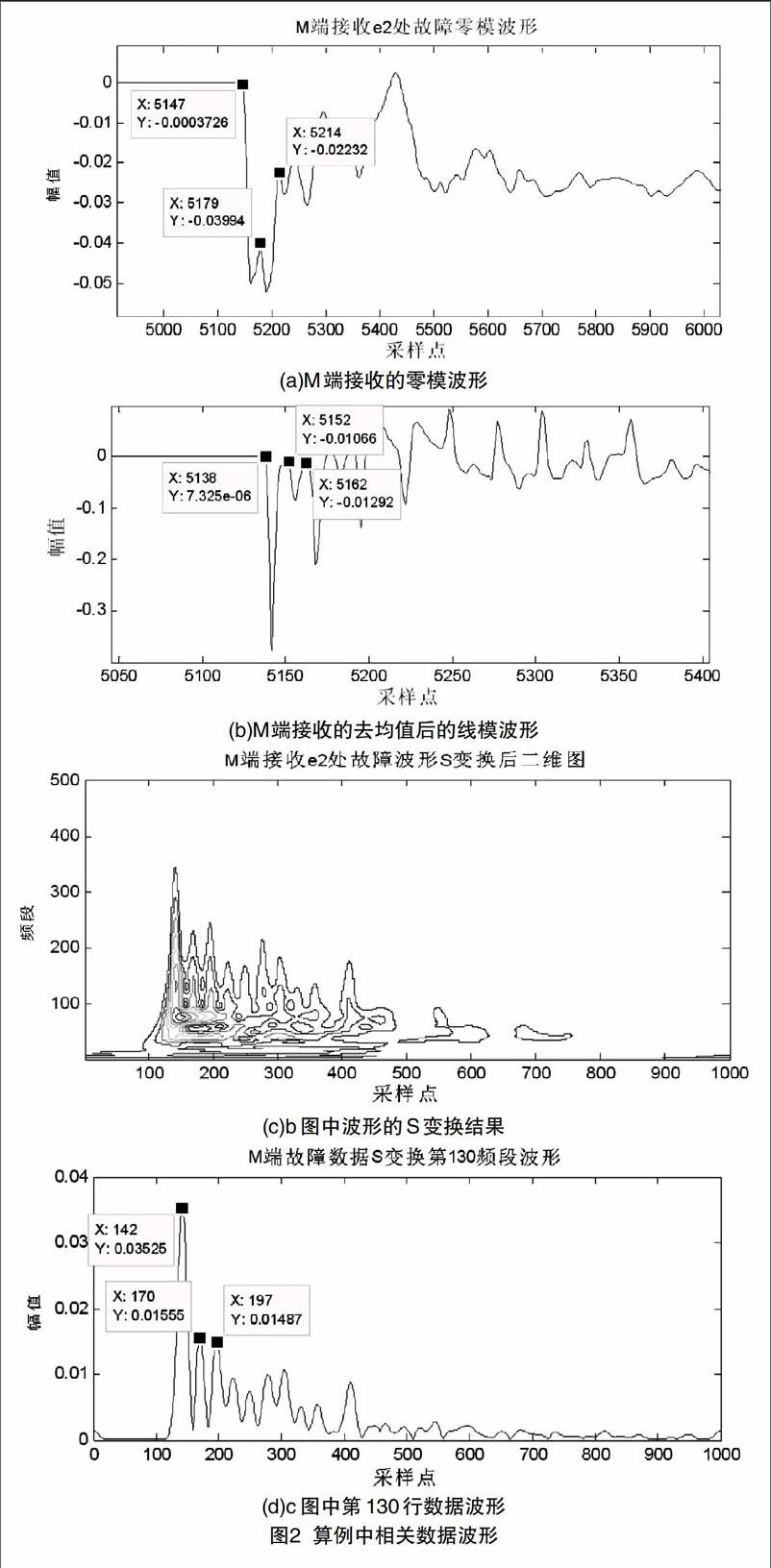
对线模数据进行S变换后结果如图2c所示,图2d为图2c中幅值最高点所在行数据,定义次数据为S变换后的关键数据,用于后续的定位算法。这里简要分析一下S變换用于配网故障数据的优势。
(1)S变换后数据更直观。传统的行波法判断行波到达时刻依靠观察波形的转折点实现,但是实际中转折点的出现是一个渐变的过程,转折点的判断受主观因素影响较大,由于行波速度很高,采样率低的时候几个点的差别会可能会造成几公里的误差,这显然不利于工程应用。基于S变换改进后,只需要在选择好的特征频点波形上读取极值点即可,工程实际中也可以很方便地借助程序实现,从而避免了主观误差。
(2)高阻接地情况仍能保持精度。众多文献显示高阻接地时,上升沿变化更加缓慢,依靠转折点判断波头到达时刻会有更大误差,而大量仿真结果显示,S变换仍能保持精度,几乎不受接地电阻的影响。
(3)可以更多地提取行波折信息,简化设备需求。图2a中可以明显看出零模线模行波除了初始波头可以利用,后续的波头因为畸变严重几乎无法提取出较精确的有用信息。因此传统的行波法在面对有稍微复杂的配网结构时不得不增加测量设备以多端定位法来达到目的。由图2c可看出经S变换处理后的行波信息可以清晰地标定后续行波波头,仿真结果显示其精度也可满足要求。因此使用S变换处理行波数据可以有效提取更多信息,对大部分行波故障定位算法都可以简化设备需求,显著地节约成本。
(4)S变换可以将信号特征分频段呈现,一定程度上削弱了频散效应,更精确清晰地呈现行波的折反射过程。以图2d中M端接收到的信号变换结果为例,按行波传输理论,第一个波头到达时刻应该对应图3a中行波所走路径,而第二个波头到达时刻应该对应图3b所示的在最近的一个阻抗不连续点折反射路径,根据例中采样频率,这段2Km长的折反射行程应该对应大概13~14个采样点。也就是说第二个波头到达时刻应该在第一个波头后13个点左右,图2a中零模波形由于畸变严重,误差很大,但还是能看出大概走势,第二个行波起始位置对应图3b的折反射路径,对应线模波形误差稍小,也可看出是对应图3b的折反射路径。但是图2d中S变换结果显示两个波头时刻相差28个采样点,即对应8.37Km的长度,对应了一段长度为4.18Km的折反射线路,显然这一数据对应的是图4(c)的传播路径。
综上可以看出在S变换具有把线路末端反射波和分支点反射波区分开的能力,目前对于这种现象还没有数学上的严谨解释,但笔者推测是因为分支点反射波和线路末端反射波的的频率成分不同引起的,这也说明了S变换的分频段呈现能力。这一现象对S变换应用于配网故障定位也有很大启发意义。
4 结论与展望
本文提分析了S变换的一些特性,探讨了S变换在配网故障定位中的应用及其优势,对比了其他传统的配网故障数据处理方式,指出S变换应用于配网故障行波数据分析的优势。初步的仿真结果证明了本方法的有效性。
当然本文还存在一些不足,S变换的分频段呈现特性仍然没有严谨的数学解释,还有S变换在配网故障定位算法中的具体应用还有待进一步研究。但初步的分析可知,S变换应用于配网故障定位是拥有广阔前景的。
参考文献
[1]R. G. Stockwell. Localization of the Complex Spectrum: The S Transform [J].IEEE Transactions on Signal Processing, vol.44,no.4, april,1996:998-1001.
[2]L. Cohen. Time-frequency distributions-A review [J].Proc. IEEE, vol.77, no. 7, July 1989.
[3]O. Rioul and M.Vetterli. Wavelets and signal processing [J]. IEEE Signal Processing Mag., vol. 8, pp. 14-38, 1991.
[4]Calgary Scientific, Time–frequency and time–time filtering with the S-transform and TT-transform [J]. Digital Signal Processing 15 (2005) 604-620.
[5]C.R. Pinnegar. Generalizing the TT-transform [J]. Digital Signal Processing, 19 (2009) 144-152.
[6]張钧,何正友.基于S变换的故障选线新方法[J].中国电机工程学报,2011,31(10):109-115.
[7]束洪春.利用故障特征频带和TT变换的电缆单端行波测距[J].中国电机工程学报,2013,33(22):103-112.
[8]束洪春.基于短窗数据S变换能量的缆线混合配电网络故障选线方法[J].电工技术学报,2009,24(10):152-159.
[9]李志斌.基于S变换的行波法高压输电线路故障定位[J].电测与仪表,2014,51(1):40-42.
