一种新的基于椭圆曲线的数字签名方案

崔师明

摘要：RSA是被研究的最广泛的公钥算法，是一种被广泛使用的公钥密码体制 。RSA的安全性依赖于大数的因子分解，本文研究一种椭圆曲线大整数分解难题和 RSA 公钥密码体制的可选择关联可转换环签名方案。具有一定推广意义。

关键词：椭圆曲线；数字密钥；签名

中图分类号：TN918 文献标识码：A 文章编号：1007-9416（2017）04-0123-01

1 椭圆曲线密码方案制定

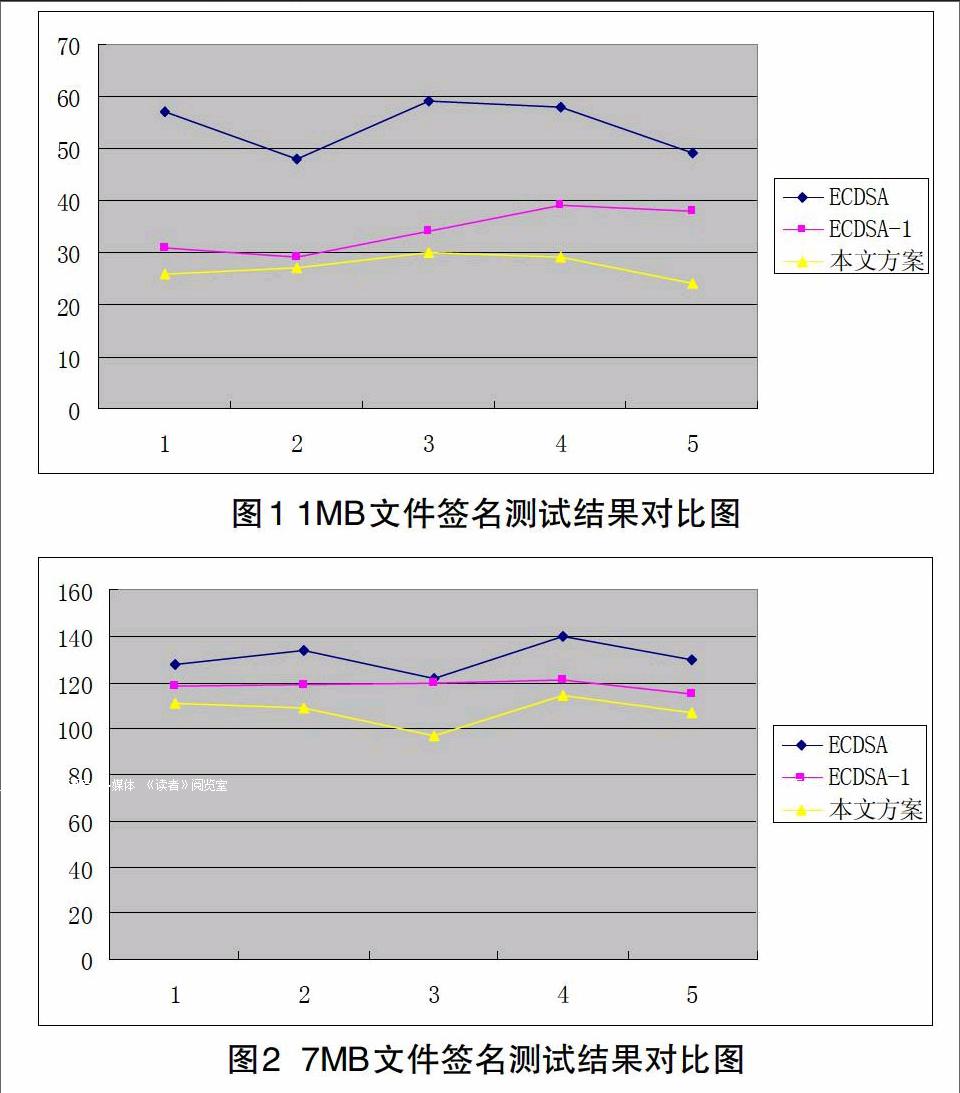
由于计算机和计时能力的局限性影响，以上结果带有一定的随机性，但基本反映算法的性能。当消息 较小时，签名方案之间的差距较大；当 较大时，签名方案的差距相对较小，但与其它方案相比，本文提出的方案运算速度更快。如图1，图2。

2 基于椭圆曲线的签名方案（ECDSA）

（1）签名过程。

1）对于待签消息，计算，并转化为一个160位的整数。

2）任意选取一个随机整数，，计算。

3）计算，如果，则返回2）重新选择。

4）计算，如果，则返回。

5 结语

本文研究椭圆曲线密码体制的簽名方案，主要研究了RSA公开密钥体制中大素数的生成原理及其算法，通过研究RSA密码体制中大素数生成的原理和方法的研究、可行性和安全性，其研究具有一定事实上的理论和实用价值。

参考文献

[1]汤锐.XML安全性研究及其在校园一卡通系统中的应用[D].北京：北京邮电大学，2007.

[2]柳翠寅，刘霞.XML签名技术的研究与应用[J].计算机应用与软件，2007，11（2）：32-35.

[3]陈赫贝，阮飞.XML数字签名及其应用研究[J].微机发展，2005，6（2）：12-15.4.