双折射对SOA中超短脉冲啁啾的影响
2017-06-02刘伟慈梁瑞生许晓慧丁南朱胜利
刘伟慈+梁瑞生+许晓慧+丁南+朱胜利
摘 要 超短脈冲通过半导体光放大器时增益变化很大,而双折射的存在,使TE模式和TM模式的光谱分布不一样。本文主要研究超短脉冲传输时其双折射效应对SOA啁啾影响。结果发现TE和TM模的啁啾随时间、波长、电流的演化差别很大,这对高速长距离光纤通信不利。因此提出了通过改变SOA波导结构和在有源区引进合适的张力来减少这种影响。
关键词 啁啾;超短脉冲;双折射
中图分类号 0437 文献标识码 A 文章编号 1674-6708(2017)185-0059-03
半导体光放大器(SOA)的宽带增益非常大;有极强的集成能力,易于与其它器件集成;能对自身损耗进行增益补偿。SOA具有高可靠性、易于小型化、价格低廉的优点,在通信市场有极大的应用。超短脉冲技术在近年来飞速发展[ 1 - 2 ],而从双折射角度研究超短脉冲下的脉冲啁啾特性甚少。超短脉冲通过SOA时增益变化很大,双折射的存在使TE模式和TM模式的光谱分布不一样,啁啾分布也存在差别,啁啾增大对高速长距离光纤通信不利,因此研究超短脉冲传输时其双折射效应对SOA中超短脉冲啁啾影响很有必要。本文采用分段模型详细分析了超短脉冲传输时双折射对信号脉冲啁啾的影响。
1 理论模型
啁啾是指光脉冲中心频率(或中心频率的移动量)随时间的变化,通常用中心频率(或频移)随时间变化的斜率表示啁啾参数,啁啾参数为正则为正啁啾,为负则为负啁啾。量子阱能带技术的发展和工程的实施,全面提高了SOA的性能,例如放大能力达到飞秒级超短脉冲。光脉冲在SOA内部传输时,受激辐射影响纵向载流子的密度,并导致增益的不均匀分布;而双折射的存在,使TE模式和TM模式的光谱分布不一样,啁啾分布存在差别。为了更准确研究半导体光放大器在超短脉冲传输时双折射对信号脉冲啁啾的影响,本文采用的模型是考虑了自发辐射噪声、有源区内载流子注入效率和端面反射系数的分段动态模型。该方程中考虑了SOA的放大自发辐射、增益谱的漂移不对称、和载流子寿命动态恢复。

本文将SOA分为41段,对载流子速率方程(3)用四阶龙格—库塔法进行数值求解,并进行模拟计算分析,结果如图所示,各图中给出了几个具有代表性的子段中的脉冲和啁啾的变化情况。
从图1可以看出,考虑端面反射时,刚开始两种模式下啁啾变化不大,保持小信号时的值,接着由于每一段的载流子浓度随着光脉冲上升沿的到来而快速减少,啁啾亦急速下降,随后缓慢恢复,最后趋于平缓,后又缓慢回升,TE模啁啾大于TM模啁啾峰值。越靠近输出端,下降和恢复的速度更快,正负啁啾峰值也越大,这是由于放大的脉冲会消耗更多的载流子。比较图1和图2,可看出,考虑端面反射时会出现多峰现象,是因为端面反射的存在使载流子的消耗产生较大的波动。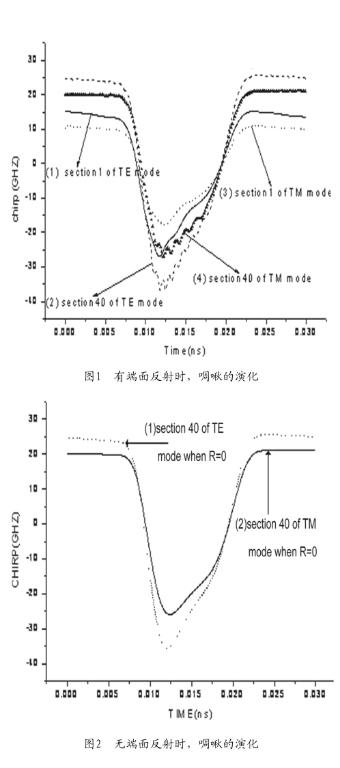

由图3可知,两种模式下正啁啾随波长的变大而缓慢上升,负啁啾虽有所波动,但总的趋势是下降,即绝对值增大。相同条件下,TE模式下的最大啁啾绝对值比TM模式时的最大啁啾绝对值大很多,说明双折射效应影响较大;而最小处两者相差不大,双折射效应影响不明显。
在图4中,两种模式下正啁啾随电流的变大而缓慢上升,负啁啾虽有所波动,但总的趋势是下降,即绝对值增大,这是由于加大电流,会使SOA中载流子密度增大,从而使增益变大,故啁啾变大。相同条件下,TE模式下的最大啁啾绝对值比TM模式时的最大啁啾绝对值大很多,并且正啁啾的相差程度大于负啁啾,说明不同的模式限制因子和微分折射率对其有较大的影响,而最小处两者相差不大,说明影响不明显。
3 结论
参考文献
[1]朱勋,谢丽虹,王干全.超短光脉冲在圆柱对称性共振介质中的传播特性[J],2009(1):44-48.
[2]JACOB C, PAMELA B, VIKRANT C, and RICK T. Measuring temporally complex ultrashort pulses using multiple-delay crossed-beam spectral interferometry[J],Optics Express,2010,18(7):6583-6597.
[3]KRISTOF O, STEPHAN K, DIRK B et al. Performance analysis of wavelength converters based on cross-gain modulation in semiconductoroptical amplifiers[J]. J. Lightwave. Technol. 1998:16(1):78-85.
[4]HENNING I, ADAMS M, COLLINS J. Performance predictions from a new optical amplifier model. IEEE J. Quant. Electron., 1985,21(6):609-613.
