含抗雷线圈的AT供电牵引网故障测距方法研究

葛海波，张家念，郭 华



含抗雷线圈的AT供电牵引网故障测距方法研究

葛海波，张家念，郭 华

基于对含抗雷线圈的全并联AT供电回路研究，提出横联电流比原理故障测距的修正方法。

抗雷线圈；故障测距；横联电流比；全并联AT供电

0 引言

目前我国高铁（客运专线）供电系统主要采用全并联AT供电方式，该运行方式常用的故障测距原理为吸上电流比和横联电流比原理。在雷击密集的铁路线路，为了保护牵引变电所内供电设备，牵引所亭馈线出口处均安装了抗雷线圈。由于抗雷线圈的存在，导致采用横联电流比原理故障测距时产生较大误差。笔者通过对含抗雷线圈的全并联AT供电回路进行研究，提出横联电流比原理的修正方法。

1 含抗雷线圈牵引网等值电路

1.1 含抗雷线圈的牵引网

目前，我国所采用的全并联AT供电方式，在AT所和分区所处将上下行接触网（T）、正馈线（F）和钢轨（R）并联连接，该供电方式牵引网可简化如图1所示，其中变电所设置2台牵引变压器，1台主用1台备用，变压器二次线圈中点抽出接地并接钢轨，在变电所馈线不设自耦变压器。CB1、CB2分别为下、上行双极断路器，AT1、AT2分别为AT所、分区所的自耦变压器，T2、F2、R2为上行线路的接触网、正馈线、钢轨，T1、F1、R1为下行线路的接触网、正馈线、钢轨，KL为牵引所亭上网处串接的抗雷线圈。

图1 全并联AT供电牵引网示意图

图2为我国高铁（客运专线）接触网横截面图，从图中可以看出下行接触线（T1）和上行接触线（T2），下行正馈线（F1）和上行正馈线（F2）均为对称布置。基于这种对称的特点，可以采用下面提到的广义对称分量法分析全并联AT供电牵引网。

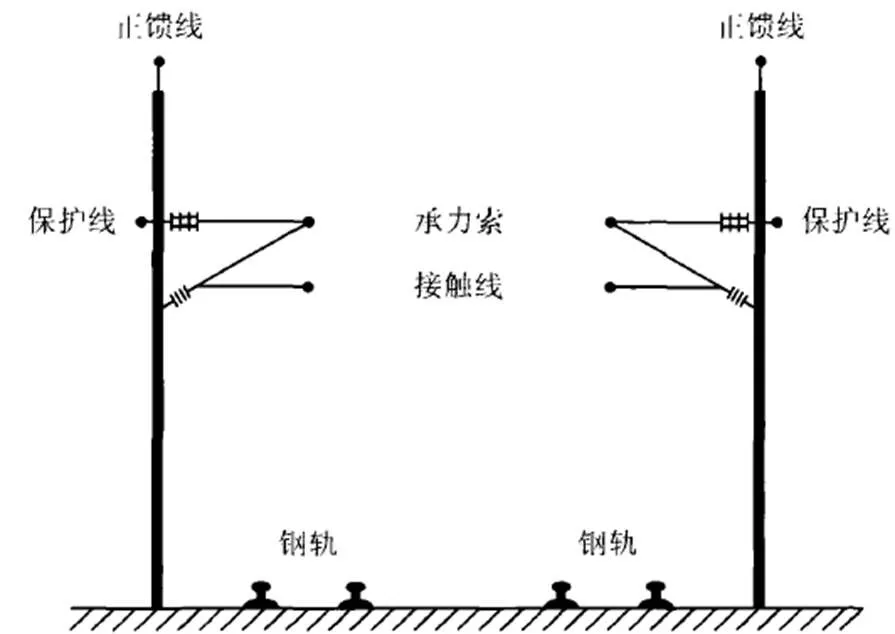
图2 全并联AT供电接触网横截面图

1.2 含抗雷线圈的牵引网等值电路

文献[1]给出了广义两相对称分量法基本概念及简单应用，此处简述如下。

当空间存在相对称子系统，且整个闭合空间有个对称布置的这种子系统时，×个物理量和×个对称分量有如下关系：

[00 01…(1-n)(1-m)] =（2）

复线全并联AT供电牵引网存在4个基本回路：T1对地、T2对地、F1对地、F2对地，通过对4个回路的阻抗进行分析，可将牵引网T1、F1、T2、F2看作是A、B、C、D四相电路。根据牵引网特性，做以下假设：（1）上下行线路参数相同；（2）AT为理想变压器；（3）接触网和正馈线自阻抗的均值作为其运算过程中的自阻抗。

上下行线的接触网和正馈线单位公里自阻抗的平均值作为每相单位公里的自阻抗：

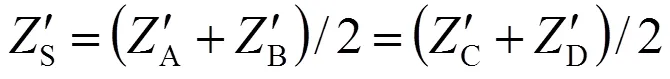
上行接触网和上行正馈线、下行接触网和下行正馈线单位公里的互阻抗为

（4）

上行接触网和下行接触网、上行正馈线和下行正馈线单位公里的互阻抗为

上行接触网和下行正馈线、上行接触网和下行正馈线单位公里的互阻抗为

（6）

由式（1）—式（6）得出全并联AT供电牵引网单位序阻抗为

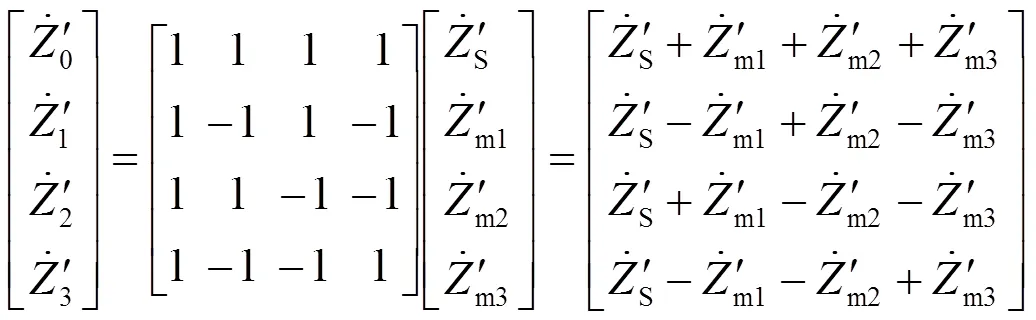
当== 2时，式（1）、式（2）中的坐标变换矩阵[]n(m)及其逆矩阵如下：

，（8）

对全并联AT牵引网的电压、电流进行坐标变换，满足如下计算式：

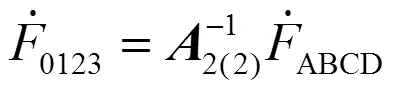
（10）

由式（10）可以得出序电流流向，如图3所示。

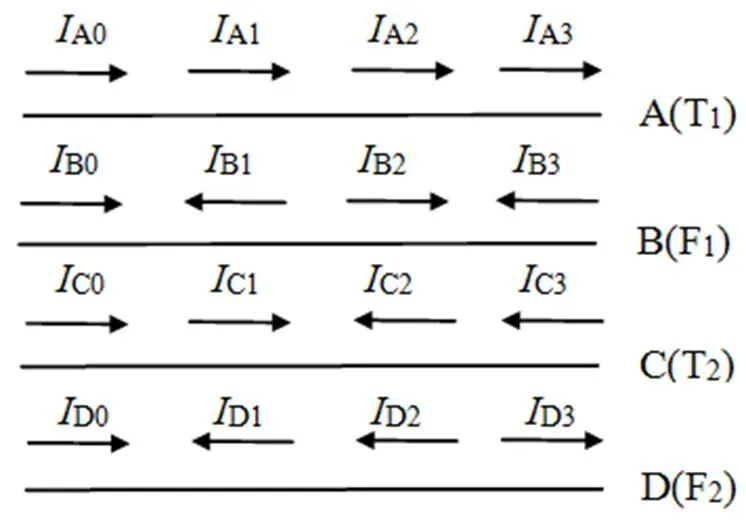
图3 序电流流向示意图

文献[1，2]均对电源、自耦变压器、横联线在各序电流流通时的特性进行了研究，本文直接引用文献[2]中的推导结果，并在推导结果中考虑增加抗雷线圈。含抗雷线圈的全并联AT供电牵引网正常序网如图4所示。

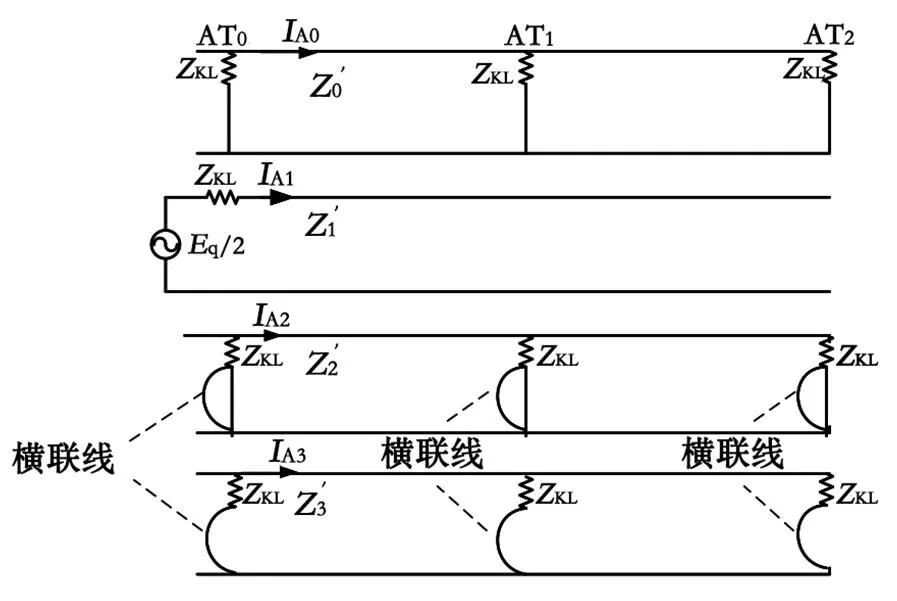
图4 含抗雷线圈的全并联AT供电牵引网正常序网图

2 含抗雷线圈牵引网横联电流比修正

对高铁（客运专线）常见的T线对地故障和T线对F线故障的修正测距公式进行推导，F线对地故障的修正和T线对地故障类似。

2.1 T线对地短路（T-R）分析

假设故障发生在AT0—AT1区段内，发生下行T线（T1）对地短路。短路电流等于T1（A）相流入大地电流，其他相直接流入大地电流为0，且T1（A）相短路点为0。所以故障电路边界条件为

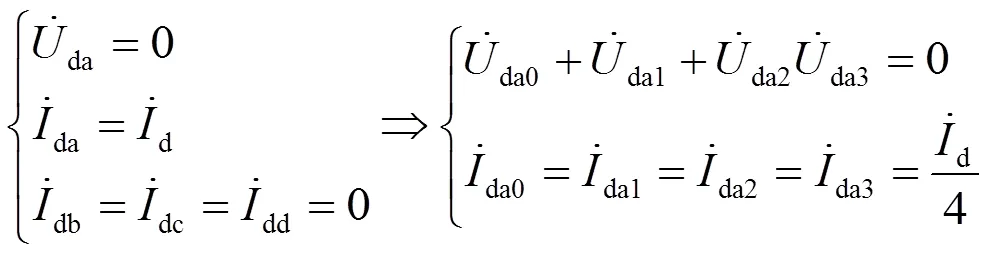
按图4可以画出下行T1（A）相故障复合序网图，如图5所示。由图5可以看出，横联电流只在2序、3序网中流通。

图5 全并联AT供电T故障复合序网图

图5中为AT0到故障点的距离，1为AT0—AT1的距离，2为AT1—AT2的距离。

AT0处横联电流为

AT1处横联电流为

（13）

式中，为AT与横联线对2序电流的分流系数。

假设：

将式（14）代入式（12）、式（13）中，得

（15）

文献[3]对复线AT牵引网序阻抗算法进行了推导，并根据实际牵引网的参数计算0序—3序阻抗，其大小分别为0.315 8+j1.781 3，0.110 6+j0.335 7，0.128 0+j0.373 8，0.113 4+j0.315 3。

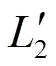
将式（11）、式（17）代入式（15）、式（16）化简可得

（18）

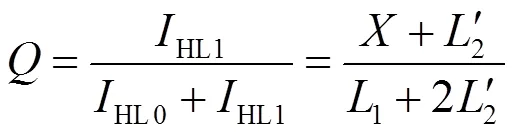
式（19）即为含抗雷线圈牵引网的横联比测距公式，当牵引网中没有抗雷线圈时，即，则式（19）可简化为

（20）

式（20）为不含抗雷线圈的全并联AT供电方式下的横联电流比计算公式。

由式（19）可得，含抗雷线圈牵引网的横联电流比测距公式为

=×(1+)-（21）

2.2 T线对F线短路（T-F）分析

假设故障发生在AT0—AT1区段内，发生下行T线（T1）对下行F线（F1）短路，即线路A、B发生短路。故障电路边界条件为

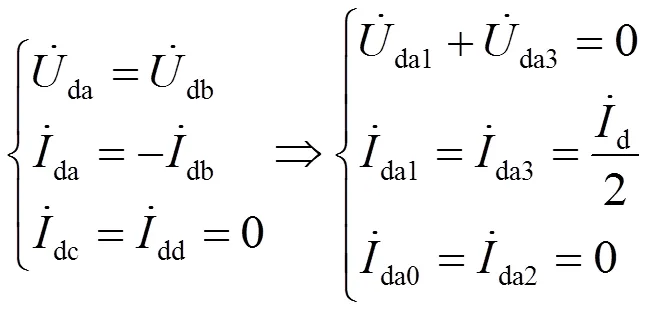
按图4可以画出下行T1—F1故障复合序网图，如图6所示，横联电流只在3序网中流通。

图6 全并联AT供电T-F故障复合序网图

AT0处横联电流为

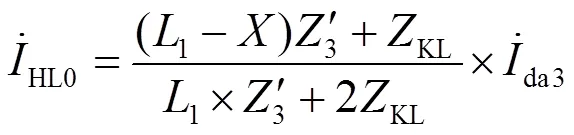
AT1处横联电流为

（24）

假设：

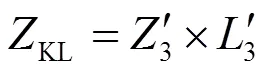
将式（25）代入式（23）、式（24），简化得

（26）

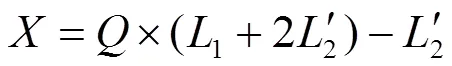
比较式（21）和式（27）可以得出，T-R、T-F故障时含抗雷线圈牵引网的横联电流比测距公式相同。本文限于篇幅未推导F-R故障时横联电流比测距修正公式，F-R故障时横联电流比测距修正公式与式（21）、式（27）相同。

3 修正公式验证

结合上文推导得出各种故障类型下含抗雷线圈牵引网的横联电流比测距公式，下面利用贵广客专潮田变电所广州方向供电臂短路实验数据校验测距修正公式的实用性。

3.1 T-R故障

故障点在AT所—分区所下行区段，故障点距离AT所13.781 km，AT所—分区所区间长度为14.02 km。图7为短路时刻供电臂电流潮流图。

图7 第二AT段T-R故障电流潮流图

采用不修正测距式（20）计算，得

= 12.834 km，误差0.947 km。

采用修正测距式（21）计算，得

= 13.970 km，误差-0.189 km。

3.2 F-R故障

故障点在变电所—AT所上行区段，故障点距离变电所16.747 km，变电所—AT所区间长度为16.770 km。图8为短路时刻供电臂电流潮流图。

图8 第一AT段F-R故障电流潮流图

采用不修正测距式（20）计算，得

= 16.043 km，误差0.704 km。

采用修正测距式（21）计算，得

= 16.866 km，误差-0.119 km。

3.3 T-F故障

故障点在AT所—分区所下行区段，故障点距离AT所8.268 km，AT所—分区所区间长度为9.164 km。图9为短路时刻供电臂电流潮流图。

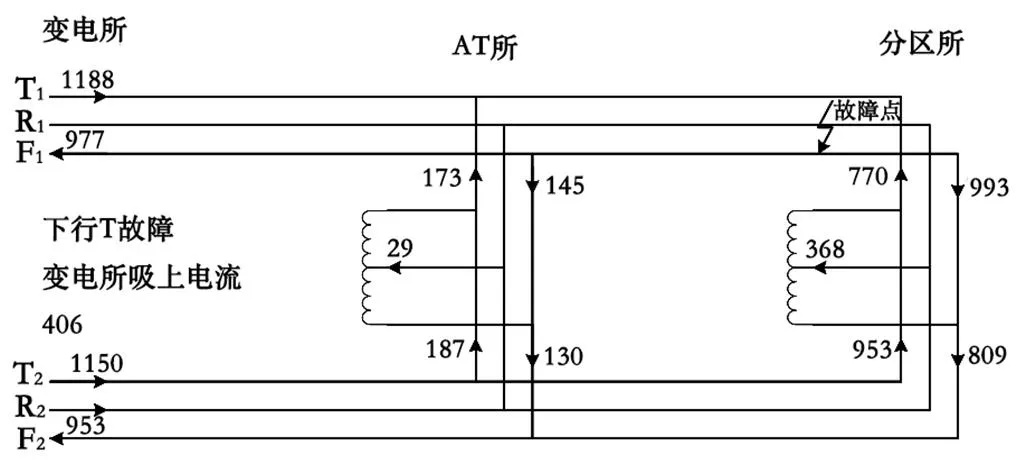
图9 第二AT段T-F故障电流潮流图

采用不修正测距式（20）计算，得

= 7.760 km，误差0.508 km。

采用修正测距式（27）计算，得

= 8.515 km，误差0.247 km。

4 结语

利用广义对称分量法对含抗雷线圈的全并联AT供电牵引网进行了分析，推导出在T-R、F-R、T-F三种故障类型时横联电流比测距公式，结果均相同。最后采用现场实际短路数据对修正测距公式进行了验证，结果表明采用修正测距公式计算故障距离误差明显变小。在利用修正测距公式时，等效长度和故障类型有关。

[1] 王凤华. 广义对称分量法及其应用[[J]. 西南交通大学学报，1981，16（1）：1-12.

[2] 林国松. 牵引供电系统新型保护与测距原理研究[D]. 成都：西南交通大学博士学位论文，2010.

[3] 马庆安. 高速铁路供电若干问题的研究[D]. 成都：西南交通大学博士学位论文，2013.

[4] 李群湛，贺建闽. 牵引供电系统分析[M]. 西南交通大学出版社，2007.

[5] 曹建猷. 电气化铁道供电系统[M]. 北京：中国铁道出版社，1993.

On the basis of researches of full parallel AT power supply circuit equipped with lightning arrestor, the paper puts forward the current ratio of cross coupling based modification method for fault location.

Lightning protection reactor; fault location; current ratio of cross coupling; full parallel AT power supply system

U223.8+3

B

1007-936X(2017)02-0009-05

葛海波.成都交大许继电气有限责任公司，工程师，电话：13540609002；张家念.南宁铁路局南宁供电段，工程师；郭 华.成都交大许继电气有限责任公司，工程师。

2016-05-13