基于米兰科维奇理论的高精度旋回识别与划分
——以南图尔盖盆地Ary301 井中侏罗统为例
2017-06-01石巨业金之钧刘全有黄振凯
石巨业,金之钧,刘全有,黄振凯
1.页岩油气富集机理与有效开发国家重点实验室, 北京 1000832.中国地质大学(北京)能源学院,北京 1000833.中国石油化工股份有限公司石油勘探开发研究院,北京 100083
基于米兰科维奇理论的高精度旋回识别与划分
——以南图尔盖盆地Ary301 井中侏罗统为例
石巨业1,2,金之钧1,3,刘全有1,3,黄振凯1,3
1.页岩油气富集机理与有效开发国家重点实验室, 北京 1000832.中国地质大学(北京)能源学院,北京 1000833.中国石油化工股份有限公司石油勘探开发研究院,北京 100083
将天文轨道周期与不同级别的旋回联系起来,旨在使米兰科维奇周期这一高精度时间标尺纳入高频层序地层划分中,实现高精度旋回的识别与划分。以哈萨克斯坦南图尔盖盆地Aryskum地堑Ary301井为例,基于不同沉积特征,分别对卡拉甘塞组I~IV段自然伽马测井数据进行频谱分析和连续小波变换,结果显示沉积地层中保存完好的米兰科维奇旋回,天文轨道周期对Aryskum地堑沉积过程具有明显影响,并将31.9~39.5 m旋回厚度解释为受400 kyr长偏心率周期控制,11.9~14.2 m,6.7~8.8 m旋回厚度分别受125 kyr和95 kyr短偏心率周期控制。对长、短偏心率周期进行滤波分析后,与天文模型理论周期曲线进行对比,建立卡拉甘塞组的浮动天文年代标尺,分别以400 kyr、125 kyr偏心率周期滤波曲线作为中期和短期旋回划分的参考曲线,共识别出11.5个中期旋回和47个短期旋回,为高频旋回划分提供了一种不受人为因素影响的天然标准,保证了研究区旋回划分的科学性和统一性。
南图尔盖盆地;米氏旋回;频谱分析;天文年代标尺;高频层序
0 引言
20世纪初,塞尔维亚科学家Milankovitch[1]提出北纬度地区夏季日照量的变化是驱动全球冰期旋回的主要原因,但该假说在很长一段时间内没有被大多数人所接受。直到1976年,Haysetal.[2]对印度洋的两个钻孔的氧同位素做了详细的古气候研究,证实了米兰科维奇提出的冰期旋回与地球轨道周期理论的正确性,并引起了地质学家和古气候学家对米兰科维奇理论的重视。近30多年来,基于古气候研究的米兰科维奇旋回理论获得了普遍认可和广泛应用,深海、湖泊、三角洲甚至滩坝沉积记录中不断被证实有米兰科维奇旋回信号的存在,梅冥相[3]将米级旋回进一步解释为与米兰柯维奇旋回相关异成因机制控制下的自旋回沉积的产物,从旋回的有序叠加形式到层序的识别与划分,代表了层序地层学的第三个重要进展。目前,与米兰科维奇旋回有关的天文轨道因素作为一种校准地质年代的重要方法已覆盖中、新生代地层,利用米兰科维奇理论结合放射性同位素定年进行高精度地质定年被认为是地层学解读时间的第三里程碑[4]。国内外学者将米兰科维奇旋回用于高频层序地层的划分与对比,进行了很多有益的尝试和探索。在用米兰科维奇理论建立天文年代标尺方面,吴怀春等[5]对松科1井的自然伽马曲线进行小波分析和连续滑动窗口频谱分析,识别了稳定的米兰科维奇旋回并建立青山口组的“浮动”天文年代标尺。尹青等[6]以伦坡拉盆地西伦2井为研究对象,利用频谱分析、滤波、Fischer图解等方法,建立了丁青湖组天文年代标尺并进行旋回地层层序划分,丁青湖组共保存了37个长偏心率周期、120个短偏心率周期,平均速率4.75 cm/kyr,沉积时限约为14.99 Myr。在用米兰科维奇理论划分高频层序方面,王艳忠等[7]以声波时差和电阻率曲线交会得到的ΔLogR为研究对象,利用小波分析刻画深水砂砾岩和泥页岩地层的内部旋回的结构。毛凯楠等[8]以琼东南盆地梅山组和三亚组地层为例,识别米兰科维奇旋回并以偏心率短周期曲线作为五级层序划分参考曲线,对研究区进行高频旋回划分与对比。任金锋等[9]基于连续小波变换进行测井信号多尺度分析,实现不同级次层序界面的定量识别与划分,在南堡凹陷W1井东营组一段划分出多个准层序和准层序组。袁学旭等[10]以东海西湖凹陷钻井为例,以米兰科维奇旋回为标尺进行测井层序划分对比,建立西湖凹陷古近系—新近系层序地层格架。郭少斌等[11]对柴达木盆地第四系自然伽马测井曲线频谱分析,结果表明地层中保存米兰科维奇旋回,并绘制可容纳空间变化曲线。在用米兰科维奇理论划分古沉积环境演化阶段方面,吴淑玉等[12]以北黄海东部坳陷为研究对象,对3口井自然伽马和自然电位测井曲线进行频谱分析,发现沉积地层中保存较好的米兰科维奇旋回,并依据不同的气候变化特征划分六个沉积阶段。谭先锋等[13]利用测井资料、录井剖面、岩芯观察以及为地球化学元素等手段,对济阳坳陷古近系孔店组高频韵律旋回沉积机制进行了深入研究。综上所述,米兰科维奇旋回周期不仅可以作为提高定年精度的天文年代标尺,在高频层序划分对比、古沉积环境演化阶段划分等方面都有广泛的应用。
选择南图尔盖盆地Aryskum地堑Ary301井为研究对象,运用米兰科维奇理论及旋回地层学手段,对Ary301井卡拉甘塞组I~IV段自然伽马测井曲线进行频谱分析、连续小波变换和滤波等分析,识别米兰科维奇旋回,建立卡拉甘塞组天文年代标尺并对比于中短期旋回。对Ary301井GR测井曲线进行高斯带通滤波,以400 kyr长偏心率周期曲线作为中期旋回划分参考曲线,以125 kyr短偏心率周期曲线作为短期旋回划分参考曲线,建立高精度的层序地层格架,旨在将米兰科维奇旋回理论引入高频层序地层划分中,为高频层序单元的划分与对比提供一种新的有效的方法。
1 区域地质背景
图尔盖盆地位于哈萨克斯坦中部,大地构造位置上处于乌拉尔—天山缝合线转折端剪切带,为典型的中生代裂谷盆地[14],总面积约8×104km2,Aryskum地堑位于南图尔盖盆地的西南部,为南图尔盖盆地的主要生油坳陷,呈南北向长轴状分布(图1)。受燕山、喜玛拉雅等构造运动的影响,Aryskum地堑发育北西—南东向断裂,其规模较大,延伸距离较远,断裂下至基底上至地表,控制着垒—堑相间的盆地结构[15]。Aryskum地堑主要沉积侏罗纪—白垩纪地层,除早古生代变质岩基底,以陆相成因碎屑岩沉积为主,并可分为上下两个构造层,下构造层为由T3~J3陆缘碎屑岩组成裂谷阶段沉积,可以分为三个沉积旋回:T3~J1、J2、J3,每一个沉积旋回是以粗碎屑岩开始,细粒泥岩结束。上构造层主要为早白垩世以上地层,与下伏地层呈不整合接触。盆地侏罗纪至早白垩世发育3期大规模湖泛,即早侏罗世末期、中侏罗世中期和早白垩世早期。大规模湖泛期发育的厚层、广泛分布的泥岩层既是有效的烃源岩,又是下伏地层的有效盖层,具有良好的生储盖组合条件。中侏罗统上部卡拉甘塞组(J2kr)经历了盆地第二次大的湖泛,粉砂岩与泥岩互层发育,且地层保存完整旋回性较强,对环境和气候变化反映灵敏。
Ary301井位于Aryskum地堑的西北部,钻遇侏罗系由下而上为鲍金根组、萨基姆拜组、爱巴林组、多尚组、卡拉甘塞组、库姆科尔组和阿卡沙布拉克组,其中中侏罗统上部卡拉甘塞组深度为1 825.5~2 306 m,地层厚度为480.5 m。根据地震、岩芯、钻测井等资料综合分析,Ary301井卡拉甘塞组为一个三级层序SQ6[16],可划分四种沉积亚相类型由下至上分别为I~IV段,依次为三角洲平原、三角洲前缘、滨浅湖和三角洲前缘亚相。
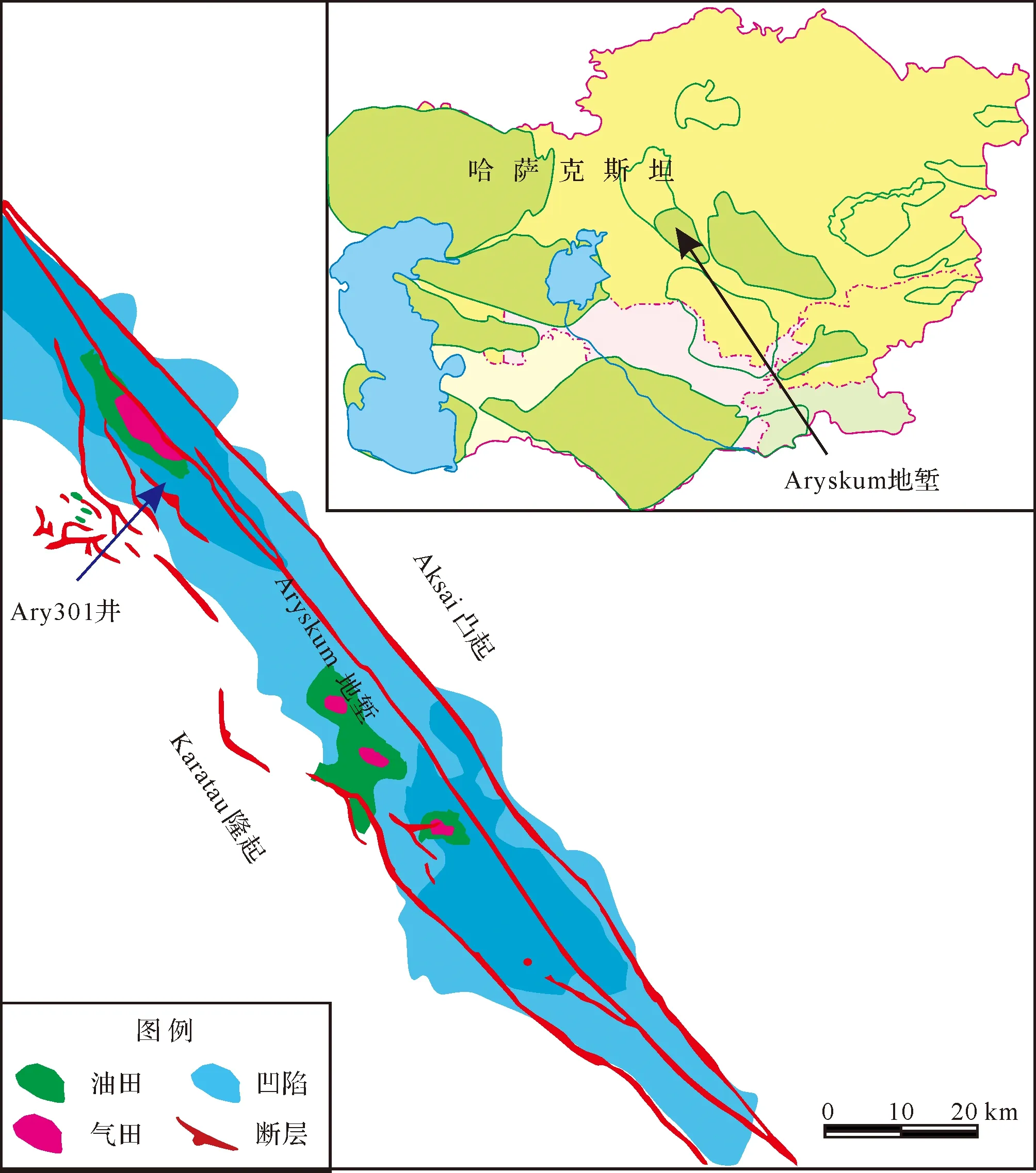
图1 南图尔盖盆地Aryskum地堑地理位置和构造分区图Fig.1 The position and tectonic map of the Aryskum graben in the South Turgay Basin
2 轨道周期与级别划分
2.1 地球轨道参数与气候变化
天文轨道周期旋回由短到长可以分为以下四个频带:天历年段、太阳频段、Milankovitch(米兰科维奇)频带和其他频段,相比而言,米兰科维奇频段在古气候研究中最为深入,这是因为轨道尺度气候变化具有明确的驱动力,即太阳系各星体作用于地球的引力场的周期性摄动,地球自转和公转时由于与太阳、月亮和其他行星之间的引力导致地球轨道参数发生周期性摄动,这些近似周期性的变化可以用偏心率(Eccentricity)、斜率(Obliquity)和岁差(Precession)来表达。斜率即为地球轴心的倾斜度,表示地球公转轨道面和地球赤道面的夹角,斜率以~41 kyr、~39 kyr和~54 kyr为主要周期在22.1°~24.5°之间变化,当前值为23°27′。在地质历史时期,由于潮汐耗散作用,地球转速变慢,所以斜率周期要比现在短,如在四亿年前地球的斜率周期主要为~32 kyr和~41 kyr[17]。正因为斜率的存在地球上才有四季,地轴斜率的大小主要影响季节气候的差异程度,并且对两极影响大对赤道影响小。斜率越大,高纬度夏季接受的太阳辐射量增加冬季减少,季节差异越大,即冬季更冷夏季更热。反之,斜率较小时,夏季相对较凉,有利于出现冰期[18]。偏心率指轨道偏离正圆的程度,偏心率值在0.000 5~0.0607范围内(现今值为0.016 7)周期性变化,变化周期分为~95 kyr、~123 kyr的短偏心率周期和~405 kyr的长偏心率周期,这种周期性的变化是由于其他行星的运动产生的万有引力作用在地球轨道上造成的,地球绕太阳公转的轨道在近圆形和椭圆形之间变化,偏心率主要是调节岁差变化幅度来影响气候,偏心率越大则岁差起伏越大四季变化越明显,而冰期普遍发育于偏心率极小值[19]。岁差是由于月球和太阳对地球赤道隆起部分的吸引,地球自转轴的方向会环绕与黄道面的垂直轴作缓慢的进动,在空间上描绘出一个圆锥面,这种现象叫岁差。岁差主周期约为24 kyr、22 kyr、19 kyr和17 kyr,在地质历史时期,受潮汐和气候摩擦作用,岁差的周期要比现在短,目前岁差周期~26 kyr年,地轴指向北极星。岁差本身并不影响地球表面日照量分布,但与偏心率结合生成一个新的气候岁差便可以影响辐射量的季节分布。如果北半球夏至到达近日点,而冬至到达远日点,那么夏季就会变的短而热,冬季就会变得漫长而寒冷,即季节性增强[20]。
地球轨道参数的变化,造成地球表面单位面积接收到的日照量变化,日照量变化会改大气环流的位置,使气候带发生纬向移动,引起大气温度、海洋环流和降雨量的变化,气候又影响冰川活动、河流、风的强弱进一步控制风化作用、搬运作用和沉积作用。日照量变化还可影响湖泊注入营养物质的总量、湖泊的蒸发以及海湖的循环作用等。总之,所有这些相互联系的因素都会最终控制沉积产物,并在地层中以岩性、岩相或地球化学参数的韵律性或旋回性表现出来,形成了与天文轨道旋回周期一致的地层旋回。
2.2 旋回级别划分和控制因素
层序地层学是以不整合面和与之对应的整合面作为边界对地层进行划分和对比的一门学科,早在1948年,Slossetal.[21]学者率先提出“层序”的概念,在1991年以Vail为代表的经典层序地层学派将层序与全球海平面变化联系起来,并提出层序发育的四大控制因素,将层序地层学推向了具有完整体系的理论阶段。层序地层学把沉积层序的成因大胆解释为全球海平面周期性变化的结果,为全球性的地层对比提供了一个有效途径,并把层序地层学带入了一个新的阶段。海平面变化主要有两种基本驱动机制,第一种是构造型海平面变化,由全球性或区域性的构造运动导致地壳升降和洋盆体积发生的变化,以周期长、速度慢为特征。第二种是冰川型海平面变化,是指温度气候变化导致大陆冰川的消长而使海水总量发生的变化,以周期短、速度快为特征。不同学者对不同级别的旋回或层序级别与海平面周期旋回的划分意见分歧很大。Vailetal.[22]于1977年根据海平面变化周期把层序分为6个级别,并于1991年对地层模式进行精炼且修正了层序的时限[23],1级至6级依次为:大于50 Ma,3~50 Ma,0.5~3 Ma,0.08~0.5 Ma,0.03~0.08 Ma,0.01~0.03 Ma,这里主要是将三级层序时限由1~10 Ma修改为0.5~3 Ma,为了将三级层序归为冰川型海平面变化的结果,但梅冥相等[24]等认为这种修改并不合理,梅冥相[25]也于2005年提出超层序、大层序、层序、亚层序、准层序组、准层序和韵律层7个级别,形成时限见表1。王鸿祯等[26]把沉积层序划分为大层序、中层序与层序组、层序、亚层序、小层序和微层序6个级别,并讨论了海平面旋回变化的成因理论。郑荣才等[27]以多个断陷盆地为例,建立不同基准面旋回划分标准,提出了出巨旋回、超长周期、长周期、中期、短期和超短期6种基准面旋回划分方案,离定了各级次基准面旋回的时间跨度,并且认为前三种类型主要受构造因素控制,后三种类型主要受天文因素控制(表1)。
各家重说纷纭,但总体来说,在以下两方面取得许多共识:1)一级到三级旋回或层序统称为长周期层序,并归为构造型海平面变化的产物,即由于构造运动引起的洋盆体积变化造成海平面周期性变化。2)四级到六级旋回或层序统称为短周期层序或高频层序,并归为冰川型海平面变化的产物,即地球轨道参数引起气候变化导致海水体积的变化,进而造成海平面周期性变化。一级海平面变化对应一级层序,形成时限在100~400 Ma周期内,普遍解释为超银河年周期,与银河系和地球圈层演化场有关。二级海平面变化对应二级层序,形成时限在30~40 Ma周期内,解释为银道周期,与太阳和银河系轨道场有关。三级海平面变化对应三级层序,即层序地层学中提到最多的“层序”,形成时限在1~10 Ma周期内,解释为小行星群轨道周期,与太阳和小行星群场有关。四级、五级海平面变化分别对应四级和五级层序,形成时限分别在0.2~0.8 Ma和0.04~0.16 Ma周期内,与长米兰科维奇周期有关,受地球轨道参数长、短偏心率控制,六级海平面变化对应六级层序,形成时限在0.02~0.04 Ma周期内,与短米兰科维奇周期有关。一般来说,长米兰科维奇旋回的长偏心率(~400 kyr)、短偏心率(~100 kyr)周期对应着层序中的准层序组或体系域,而短米兰科维奇旋回的斜率(~40 kyr)和岁差(~20 kyr)周期对应于准层序或韵律层。
表1 旋回级次划分和基本特征(据参考文献[22~26]修改)
Table 1 Classification and basic characteristics of cycles

旋回级别一级二级三级四级五级六级形成时限/Ma(本文建议)>5030~401~100.2~0.80.04~0.160.02~0.04层序地层术语巨层序超层序层序准层序组或体系域准层序韵律层海平面变化类型构造型冰川型天文旋回克拉通热旋回穿越银道面旋回奥尔特旋回长米氏旋回短米氏旋回旋回周期超银河年周期银道周期小行星群轨道周期长偏心率周期短偏心率周期斜率周期岁差周期场类型银河系与地球圈层演化场太阳—银河系轨道场太阳—小行星群场地球轨道场Vailetal.[23]I>50I3~50III3~0.5IV0.5~0.08V0.03~0.08VI0.03~0.01郑荣才等[27]巨旋回 30~>100超长期旋回10~50长期旋回1.6~5.25中期旋回0.2~1短期旋回0.04~0.16超短期旋回0.02~0.04梅冥相等[25]超层序300~290大层序30~40层序1~10亚层序1~0.5准层序组(0.4)准层序(0.1)韵律层<0.04王鸿祯等[26]大层序60~120中层序 25~40层序组 8~15层序2~5亚层序0.8~1.5小层序0.1~0.4微层序0.02~0.04
3 理论与方法
3.1 数据选择与分析方法
在一段地质历史时期内,地球轨道参数的周期变化缓慢,具有相对稳定性,而其之间的比率是判断地层中是否存在米兰科维奇旋回的重要指标。普遍观点认为,如果能在地层记录中找到可以与地球轨道三要素(偏心率、斜率、岁差)之间有相同比率关系的沉积旋回或周期,我们就认为该段地层受米兰科维奇旋回的影响。同时也要注意一下三点:1)沉积的连续性,在进行米兰科维奇旋回分析时,该段地层的沉积一定要连续,中间不可以有间断或不整合面。2)沉积速率相对稳定,在深度域进行频谱分析时,只有沉积速率相同,沉积地层厚度的比值才是沉积时间的比值。3)替代性指标要选取与气候或湖平面变化有关的信号。
替代性指标是指对古气候或古环境反映较为敏感的一些岩性、地球物理或地球化学等参数,从而构建反映古气候变化的时间序列来进行定量分析[28-30]。自然伽马(GR)测井是测量沉积物中伽马射线的强度,可以敏感第反映沉积物中泥质含量,进而反映古气候和古环境的微小变化,是米兰科维奇旋回分析的理想数据,因此本次使用GR测井曲线作为替代性指标进行地层旋回分析,计算优势厚度提取对应的米氏旋回信号,在三级层序内划分建立更高精度的地层格架。
在信号分析之前,首先要对数据进行预处理,以剔除所构建时间序列中各类环境“噪音”。数据预处理可以分为以下几步:1)插值与重采样,由于一些软件以及算法的限制,时间序列分析必须等间距,而一些野外的地质数据难免会有不等间距采样的情况,所以必须先进行等距离的重采样。2)去极值,去除序列中偏离均值很大的异常点。3)去趋势化,某些序列出现趋势性变化会在频谱图中出现极高振幅,除去这些高能量的低频成分也是必要的。4)预白化,主要是削弱比重较大的低频成分,而使各个频率成分大致相当,压制低频信息,提高高频信息。5)滤波,主要包括高通、低通或带通滤波,可以剔除与米兰科维奇旋回无关的高频或低频信息。以上这些都可以用matlab软件编写程序或Analyseries 2.0进行时间序列的预处理。
频谱分析可以识别出时间序列中的周期或准周期成分,将谱图中峰值对比于理论轨道参数的标准值,若有相同的比值,即判断该地层记录着米兰科维奇旋回信号。连续小波变换具有时频局部化和多尺度分析的特点,可将测井信号中蕴含的不同尺度的信息提取出来,表现出时间域(位移因子)和频率域(尺度因子)的二维信息,有利于揭示地层中隐藏的旋回性,更直观的识别米兰科维奇信号[31-32]。值得注意的是,时间序列的频率是信号出现的次数与时间的比,倒数即为周期,而深度序列的频率是指信号出现的次数与厚度之比,倒数为厚度,用厚度比值与轨道周期理论值作比较的前提是沉积速率不变,因此,如果使用地层组或三级层序为界进行频谱分析是需要慎重考虑的,不同沉积相带的沉积速率差别往往较大,在此本文基于不同沉积亚相对各段GR曲线进行连续小波变换和频谱分析。
3.2 计算理论轨道周期
地球轨道参数(偏心率、斜率和岁差)周期性变化控制着地球表面接受日照量强度和时间的变化,进而促使气候变迁并记录在沉积序列之中,这些记录在沉积地层之中的高频旋回也被称为“米兰科维奇旋回”。实践证明,长、短偏心率旋回在漫长的地质历史时期中是稳定的,这种稳定的地层记录构成了一组约1:4的叠加形式(若地层沉积速率不变,~400 kyr的长偏心率周期和~100 kyr的短偏心率周期形成地层厚度比为1:4),因此100 kyr准周期还被誉为地支计时的“天文钟摆”[33]。但由于潮汐耗散和气候摩擦的作用,在地质历史时期地球自转速度变慢,岁差和斜率周期就不那么稳定而会有不同程度的变化。天文学家综合考虑太阳系中各行星运动以及相互作用而设计出各种天文解决方案,可以根据此天文解决方案计算出距今250 Myr以内的天文轨道信号大小。
本文采用LA2004标准模型[33]的斜率和岁差方案(Laskaretal., 2004)以及LA2010标准模型的偏心率d方案(Laskaretal., 2011),以1kyr为采样间隔,计算了中侏罗世163.5~174.1 Myr期间偏心率(E)、斜率(T)和岁差(P)周期变化的理论值,并且计算了标准化(每个参数范围限定在0~1)以后的偏心率、斜率和岁差之和,即标准ETP曲线,类似全球日照量曲线用来反映地球轨道参数之间综合的特点。对以上理论数据进行频谱分析后,得到3个偏心率周期:400 kyr(E3)、125 kyr(E2)和95 kyr(E1),2 个斜率周期:44 kyr(T2)、36 kyr(T1),3个岁差周期:22 kyr(P3)、21 kyr(P2)、18 kyr(P1),其相互之间的比值为1∶0.313∶0.238∶0.11∶0.09∶0.055∶0.053∶0.045(图2)。本次研究以这些理论轨道周期及其比值为基准。
4 分析结果
Ary301井卡拉甘塞组深度为1 825.5~2 306 m,地层厚度为480.5 m,采样间隔0.125 m,GR数值范围为43~170 API,平均值为96 API中位值为106 API,由下至上分别发育三角洲平原、三角洲前缘、滨浅湖和三角洲前缘亚相,钻井深度依次为2 168~2 306 m、2 052~2 168 m、1 948~2 052 m和1 825.5~1 948 m,低值与砂岩相对应,高值与泥岩对应,显示出较好的旋回性。笔者对Ary301井1 825.5~2 306 m井段的GR测井曲线基于沉积特征进行分段小波变换和频谱分析,分别对应着I~IV段四种沉积亚相类型。
在深度域上对Ary301井I段的伽马测井数据序列进行频谱分析,频谱图中显示出7个优势频率峰值a、b、c、d、e、f、g,其频率分别为0.025 3、0.070 5、0.113 8、0.159 0、0.229 4、0.484 2、0.520 3(图3a)。谱图中横坐标代表深度序列的频率(旋回个数/m),纵坐标代能量强度,即该频率所占比重。因此,谱峰对应的旋回厚度(1/频率)为39.5 m、14.1 m、8.8 m、6.3 m、4.4 m、2.1 m、1.9 m。陆相沉积的沉积速率普遍比海洋的高,按陆相的平均沉积速率100 m/Myr计算,405 kyr平均沉积40.5 m左右沉积物,因此以峰值a作为基准,对应的旋回厚度比为1.00∶0.36∶0.22∶0.16∶0.11∶0.052∶0.048。而根据Laskar标准模型算出中侏罗世的天文周期为400 kyr(E3)、125 kyr(E2)、95 kyr(E1)、44 kyr(T2)、21 kyr(P2)、18 kyr(P1),其之间比例为1.00∶0.313∶0.238∶0.11∶0.053∶0.045。可以发现,除d可能由非米兰科维奇旋回信号影响之外,a、b、c、e、f、g均与天文轨道周期变化有良好的对应关系。同样在深度域上对该段数据序列进行连续小波变换,其小波分析图中显示较为连续的37.8~46.5 m、14.2~18.1 m、3.9~5.1 m和1.9~2.2 m的四段沉积旋回,与163.5~174.1 Myr期间的地球轨道参数长偏心率E3、短偏心率E2、斜率T2与岁差P有较好的对应关系,频谱分析与连续小波分析说明该段伽马数据确实存在米兰科维奇信号,而非偶然因素的影响。因此,在I段~39.5 m、~14.2 m、~8.8 m、~4.4 m、~2.1 m和~1.9 m沉积旋回分别解释为由长偏心率E3、短偏心率E2、短偏心率E1、斜率T2、岁差P2和岁差P1引起的,而且谱图中偏心率信号更强,是影响该地区地层旋回的主要因素,用偏心率周期引起的旋回地层厚度除以偏心率周期得到沉积速率为98.8 m/Myr,由于未考虑到脱压实校正,本文计算沉积速率为现今条件下的“视沉积速率”。
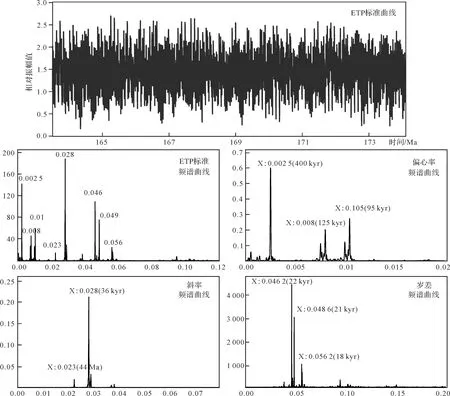
图2 163.5~174.1 Ma期间的ETP、偏心率、斜率和岁差的频谱图(据Laskar et al.[34]计算)Fig.2 The spectrum of ETP, eccentricity, obliquity and precession in 163.5~174.1 Myr(calculated from Laskar et al.[34])
Ary301井II段的伽马测井数据序列在深度域上的频谱图中显示出8个优势频率峰值a、b、c、d、e、f、g、h,其频率分别为0.015、0.028、0.084、0.142、0.235、0.315、0.478、0.556(图3b),对应的旋回厚度为66.7 m、35.7 m、11.9 m、7.0 m、4.3 m、3.2 m、2.1 m、1.8 m,其中b、d、e、f、g、h分别对应400 kyr、125 kyr、44 kyr、36 kyr、22 kyr、21 kyr,本次未将峰值a厚度为66.7 m解释为长偏心率周期是考虑到沉积速率在短时期不应该有较大变化,而且对比于其他峰值把35.7 m解释为长偏心率周期更为合理。连续小波色谱图中显示较为连续的4个频带30.3~38.6 m、10.1~13.8 m、3.9~5.2 m、1.8~2.0 m,分别解释为长偏心率E3、短偏心率E2、斜率T2和岁差P周期。因此,在II段长偏心率E3、短偏心率E2、斜率T2、斜率T1控制的沉积厚度分别为~35.7 m、~11.9 m、~4.3 m、~3.2 m,该段沉积速率为89.3 m/Myr。
Ary301井III段的伽马测井数据序列在深度域上的频谱图中显示出7个优势频率峰值a、b、c、d、e、f、g,其频率分别为0.0313、0.149、0.279、0.341、0.555、0.608、0.675(图3c),对应的旋回厚度为31.9 m、6.7m、3.6 m、2.9 m、1.8 m、1.6 m、1.5 m,分别对应400 kyr、95 kyr、44 kyr、36 kyr、22 kyr、21 kyr、18 kyr。连续小波色谱图中显示较为连续的28.5~33.2 m、6.3~7.9 m、2.8~3.7 m、1.5~1.9 m,分别解释为长偏心率E3、短偏心率E1、斜率T和岁差P周期。因此,在III段长偏心率E3、短偏心率E1、斜率T2、斜率T1控制的沉积厚度分别为~31.9 m、~6.7 m、~3.6 m、~2.9 m,该段沉积速率为79.7 m/Myr。

图3 Ary301井4段小波变换及频谱分析图a.卡拉甘塞组I段GR测井曲线小波分析图;b.卡拉甘塞组II段GR测井曲线小波分析图;c.卡拉甘塞组III段GR测井曲线小波分析图;d.卡拉甘塞组IV段GR测井曲线小波分析图。图谱中红色代表能量较高,蓝色代表能量较低,锥形曲线下方为不可靠区域,主要由于小波变换的边缘效应造成。e.卡拉甘塞组I段GR测井曲线频谱分析图;f.卡拉甘塞组II段GR测井曲线频谱分析图;g.卡拉甘塞组III段GR测井曲线频谱分析图;h.卡拉甘塞组IV段GR测井曲线频谱分析图;图中红色曲线代表80%置信度曲线,绿色代表90%置信度曲线。Fig.3 The wavelet transform and spectrum analysis diagram of four segments in Well Ary301
Ary301井IV段的伽马测井数据序列在深度域上的频谱图中显示出7个优势频率峰值a、b、c、d、e、f、g,其频率分别为0.026 2、0.070 4、0.119、0.179、0.266、0.465(图3d),对应的旋回厚度为38.2 m、14.2 m、8.4 m、5.6 m、3.8 m、3.0 m、2.2 m,a、b、c、e、g分别对应400 kyr、125 kyr、95 kyr、36 kyr、22 kyr。连续小波色谱图中显示较为连续的36.2~47.1 m、14.0~16.2 m、3.7~5.2 m、1.8~2.2 m,分别解释为长偏心率E3、短偏心率E2、斜率T1和岁差P周期,因此,在IV段长偏心率E3、短偏心率E2、短偏心率E1、斜率T1控制的沉积厚度分别为~38.2 m、~14.2 m、~8.4 m、~3.8 m,该段沉积速率为95.4 m/Myr。
5 讨论
5.1 浮动天文年代标尺建立
如果能够证明地层记录中的沉积旋回是天文轨道驱动所致,便可将沉积旋回或古气候的替代性指标调谐到理论天文轨道参数的目标曲线上,将深度信号校准到时间信号上,就可获得高分辨率的天文年代标尺[35]。由于缺少精确的地质定年资料以及其他方法可以得到的年龄“锚点”,这里根据发现的米兰科维奇旋回个数以及粗略的时间边界建立相对时间概念的天文年代标尺,即“浮动天文年代标尺”。
频谱分析和连续小波变换均表明Ary301井的卡拉甘塞组四段沉积过程均受到了地球轨道参数(偏心率、斜率和岁差)的影响,而且400 kyr长偏心率E3信号最强最稳定,因此本文从Ary301井GR测井曲线中提取400 kyr长偏心率周期E3的滤波曲线为调谐曲线,125 kyr短偏心率周期E2为辅助曲线,设计出相应的高斯带通滤波器对伽马曲线的长、短偏心率分别进行滤波,长偏心率滤波参数为(0.025 6±0.008 5)旋回/m,短偏心率滤波参数为(0.076 9±0.013)旋回/m,利用调节线使调谐曲线和理论曲线谷值位置对应一致,建立卡拉甘塞组的浮动天文年代标尺。在南图尔盖盆地Aryskum地堑的层序划分方案中,卡拉甘塞组的顶界面对应着中侏罗统的顶界面,据2015年最新国际地质年表,中侏罗统顶界面(卡洛夫阶和牛津阶)地质年龄为163.5±1.0 Ma,这里卡拉甘塞组顶界面年龄粗略的采用163.5 Ma,沉积记录中共保存了约11.5个长偏心率周期,37个短偏心率周期,而每两条调谐线之间为400 kyr的一个偏心率周期,持续时间大约在4.6 Myr左右,推算出卡拉甘塞组底界面年龄约为168.1 Ma。
5.2 高频旋回识别与划分
高频旋回识别与对比在理论上可以分为三大学派,以准层序或准层序组为基本单元的Vail经典层序地层学,以Galloway为代表的主张以最大海泛面为界的成因层序地层学和以Cross为代表的高分辨率层序地层学,前两者均强调全球海平面变化控制着层序的发育及成因,主要应用于海相;而高分辨率层序地层学提出基准面、体积划分和相分异原理,强调基准面变化是控制不同层序发育的机制,不需要海平面为参考,因此不仅适用于海相盆地同样也适用于陆相含油气盆地,另外灵活运用基准面的概念可以很好解决自旋回和异旋回问题。研究区以河流、三角洲和湖泊相沉积为主,运用高分辨率层序地层学层序划分和对比技术,结合天文轨道参数的浮动天文年代标尺,实现高精度的地层单元划分与对比,建立高分辨率年代地层格架(图4)。
长期基准面旋回具有较大规模水深变化的完整湖进—湖退沉积充填序列,湖泛面一般位于层序内部泥页岩沉积的中部或顶部,具有连续沉积或沉积间断面性质,其界面成因类型受同一构造演化阶段的次级构造活动控制,与奥尔特旋回周期有关,平均沉积时限为1.6~5.25 Myr,一般相当于层序地层学中的三级层序,可在地震剖面通过地震反射终止关系判别,也可以从露头或测井岩芯中识别。Ary301井卡拉甘塞组为一个三级层序,地层厚度480.5 m,沉积时限为4.6 Myr,划分为一个长周期旋回,湖泛面位于层序中部的湖相泥质密集段,下半旋回由下至上分别发育三角洲平原—三角洲前缘—滨浅湖亚相,反映湖平面上升、可容纳空间增大、基准面逐渐上升的过程,上半旋回由下至上分别发育滨浅湖—三角洲前缘亚相,反映湖平面下降、可容纳空间减小、基准面逐渐下降的过程,总体为一个以基准面上升为主的湖进—湖退过程。
中期基准面旋回具有高幅水深变化、彼此有成因联系的地层叠加组成的次级湖进—湖退沉积充填序列,受构造和气候的双重作用控制,与米兰科维奇旋回长偏心率周期有关,平均沉积时限为0.2~0.8 Myr,相当于层序地层学中的四级层序,本文研究发现基于米兰科维奇理论划分的长偏心率旋回与微相的垂向沉积序列有较好的对应性,可以反映一定的湖进—湖退沉积充填,因此将中期基准面旋回即四级层序的时间定量化为400 kyr。中期基准面旋回通常以较大规模的冲刷面为界线,由一系列短周期基准面旋回叠置而成,往往通过测井曲线及岩性剖面特征对其进行识别。中期基准面旋回的序列主要是指亚相或微相的垂向序列,例如三角洲平原亚相→三角洲前缘亚相为基准面上升旋回,反映湖侵的过程;三角洲前缘分流间湾微相→远砂坝微相→河口坝微相为基准面下降旋回,反映湖退的过程。其顶、底界面可能对应于北半球高纬度夏半年日照量最低的冰期,偏心率主要调控岁差的周期变化幅度来影响气候变化,偏心率的极小值更容易产生冰期。因此,中期旋回的顶、底与伽马长偏心率滤波曲线的低值一一对应,共识别出11.5个中期基准面旋回。I段三角洲平原沉积亚相包含3.25个中期基准面旋回,主要发育分流河道和分流间湾微相的交互沉积,由于分流河道的普遍发育及相互叠置,上一期天然堤或决口扇微相总是被下一期河道侵蚀冲刷,基准面下降半旋回的沉积记录缺失或无沉积间断,仅保存3.25个基准面上升半旋回沉积记录。II段三角洲前缘沉积亚相包含2.75个中期基准面旋回,除中间一段基准面出现短暂下降,基准面整体还是不断上升的过程,沉积序列的叠加方式以退积或加积为主。III段滨浅湖亚相包含3个中期基准面旋回,该期的湖泛面为此三级层序的最大湖泛面,越过最大湖泛面后,基准面开始缓慢下降。IV段三角洲前缘沉积亚相包含2.5个中期基准面旋回,中段出现基准面缓慢上升,整体沉积序列以进积为主发育基准面下降旋回。

图4 Ary301井卡拉甘塞组高频旋回识别与划分a.理论周期曲线中红色曲线代表理论E3长偏心率曲线且周期为400 kyr,蓝色曲线代表理论E2短偏心率曲线且周期为125 kyr,黑色数字代表短偏心率曲线旋回个数;b.GR长偏心率滤波曲线采用高斯带通滤波方法得出,滤波参数为(0.025 6±0.008 5)旋回/m,蓝色虚线为GR原始曲线,红色数字代表长偏心率旋回个数;c.GR短偏心率滤波曲线采用同样方法,滤波参数为(0.076 9±0.013)旋回/m,红色数字代表长偏心率旋回个数,黑色数字代表短偏心率曲线旋回个数;d.GR斜率滤波曲线滤波参数为(0.26±0.02)旋回/m。Fig.4 High-frequency cycles identification and division of Karagansky Formation in Well Ary301
短期基准面旋回具有低幅水深变化、彼此有成因联系的韵律湖进—湖退沉积充填序列,受气候的干、湿变化过程控制,与米兰科维奇旋回短偏心率周期有关,平均沉积时限为0.04~0.16 Myr,相当于层序地层学中的五级层序,基于米兰科维奇理论划分的短偏心率旋回与岩相组合有较好的对应性,可以反映低幅水深变化的韵律性湖进—湖退充填,这里将短期基准面旋回即五级层序的时间定量化为125 kyr。短期基准面旋回可以直接通过露头及岩性测井资料进行识别,通常可以分为向上变深非对称型旋回(A型)、向上变浅非对称型旋回(B 型)和对称型旋回(C型)3种类型,低可容纳空间A1型、高可容纳空间A2型、低可容纳空间B1型、高可容纳空间B2型、以上升半旋回为主的C1对称型、以下降半旋回为主的C2型和上升下降半旋回对等的C3对称型7种亚类型[36]。由于三角洲平原亚相上半旋回经常遭受冲刷与侵蚀作用,但同时又阶段性发育分流间湾,说明水体下切作用相对较弱,以发育高可容纳空间A2型为主;三角洲前缘亚相可容纳空间较大,由河口坝或决口扇组成的反韵律进积结构保存完整,基准面类型以下降半旋回为主的C2型和上升下降半旋回对等的C3型为主;滨浅湖亚相以发育高可容纳空间B2型和上升下降半旋回对等的C3型为主;由下至上,共识别出37个短期基准面旋回。
超短期基准面旋回是根据岩芯或测井资料能够识别的最小成因地层单元,是受岁差周期影响形成的韵律层,也是油田开发过程中的最基本单元,即同一时期沉积的单砂体,但在此次实际工作中由于还未研究到开发过程单砂层精度,未对超短期旋回进行对比。
6 结论
(1) 地球轨道参数引起气候变化导致湖平面周期性变化是高频层序或短周期层序的主控因素,长期基准面旋回具有较大规模水深变化的湖进—湖退充填序列,与奥尔特旋回有关,相当于层序地层学中的三级层序;中期基准面旋回具有高幅水深变化的次级湖进—湖退充填序列,与米兰科维奇旋回长偏心率周期有关,相当于层序地层学中的四级层序。短期基准面旋回具有低幅水深变化的韵律湖进—湖退充填序列,与米兰科维奇旋回短偏心率周期有关,相当于层序地层学中的五级层序。超短期基准面旋回是最小成因地层单元,是受斜率或岁差周期影响形成的韵律层,相当于层序地层学中的六级层序。
(2) 采用LA2004及LA2011理论天文模型计算出中侏罗世163.5~174.1 Myr期间偏心率(E)、斜率(T)和岁差(P)分别为:400 kyr(E3)、125 kyr(E2)、95 kyr(E1)、44 kyr(T2)、36 kyr(T1)、22 kyr(P3)、21 kyr(P2)、18 kyr(P1)。基于不同沉积特征,对Aryskum坳陷Ary301井卡拉甘塞组I~IV段分别进行频谱分析和连续小波变换,发现沉积地层中均保存完好的米兰科维奇旋回,天文轨道周期对Aryskum地堑沉积过程具有明显影响,受400 kyr长偏心率周期影响的旋回厚度为31.9~39.5 m,受125 kyr和95 kyr短偏心率周期影响的旋回厚度分别为11.9~14.2 m,6.7~8.8 m,44 kyr和36 kyr斜率周期引起的地层旋回厚度分别为3.6~4.4 m,2.9~3.8 m,22 kyr、21 kyr和19 kyr岁差周期引起的旋回厚度为1.8~2.1 m,1.6~2.2 m,1.5~1.9 m。
(3) 通过对Ary301井GR测井曲线进行高斯带通滤波,提取长、短偏心率周期曲线并调谐到Laskar天文模型的理论周期曲线上,建立Ary301井卡拉甘塞组浮动天文年代标尺。卡拉甘塞组共记录了11.5个长偏心率周期和47个短偏心率周期分别对应于11.5个中期旋回和47个短期旋回,米兰科维奇旋回具有相对稳定的周期以及对高频层序的控制作用,作为高频层序划分的时间标尺,为测井层序划分提供一种不受人为因素影响的天然标准,提高了高频层序划分的科学性,保证了研究区层序划分的统一性。
References)
[1] Milankovitch M. Kanon der erdbestrahlung und seine anwendung auf das eiszeitproblem[M]. Königlich Serbische Akademie, 1941.
[2] Hays J D, Imbrie J, Shackleton N J. Variations in the Earth's orbit: pacemaker of the ice ages[J]. Science, 1976, 194(4270): 1121-1132.
[3] 梅冥相. 从旋回的有序叠加形式到层序的识别和划分:层序地层学进展之三[J]. 古地理学报,2011,13(1):37-54. [Mei Mingxiang. From vertical stacking pattern of cycles to discerning and division of sequences: the third advance in sequence stratigraphy[J]. Journal of Palaeogeography, 2011, 13(1): 37-54.]
[4] 龚一鸣,杜远生,童金南,等. 旋回地层学:地层学解读时间的第三里程碑[J]. 地球科学,2008,33(4):443-457. [Gong Yiming, Du Yuansheng, Tong Jinnan, et al. Cyclostratigraphy: the third milestone of stratigraphy in understanding time[J]. Earth Science, 2008, 33(4): 443-457. ]
[5] 吴怀春,张世红,黄清华. 中国东北松辽盆地晚白垩世青山口组浮动天文年代标尺的建立[J]. 地学前缘,2008,15(4):159-169. [Wu Huaichun, Zhang Shihong, Huang Qinghua. Establishment of floating astronomical time scale for the terrestrial Late Cretaceous Qingshankou Formation in the Songliao Basin of Northeast China[J]. Earth Science Frontiers, 2008, 15(4): 159-169.]
[6] 尹青,伊海生,夏国清,等. 基于测井曲线频谱分析在伦坡拉盆地古近系米氏旋回层序及可容空间变化趋势中的研究[J]. 地球物理学进展,2015,30(3):1288-1297. [Yin Qing, Yi Haisheng, Xia Guoqing, et al. Accommodation space and Milankovitch orbit cycle sequence of the Paleogene stratigraphic frames in Lunpola Basin based on the spectrum analysis of the logging curve[J]. Progress in Geophysics, 2015, 30(3): 1288-1297.]
[7] 王艳忠,操应长,远光辉. 小波分析在深水砂砾岩和泥页岩地层层序划分中的应用[J]. 天然气地球科学,2012,23(2):251-258. [Wang Yanzhong, Cao Yingchang, Yuan Guanghui. Application of wavelet analysis in sequence division of deepwater glutenite and shale layer[J]. Natural Gas Geoscience, 2012, 23(2): 251-258.]
[8] 毛凯楠,解习农,徐伟,等. 基于米兰科维奇理论的高频旋回识别与划分——以琼东南盆地梅山组和三亚组地层为例[J]. 石油实验地质,2012,34(6):641-647. [Mao Kainan, Xie Xinong, Xu Wei, et al. Identification and division of high-frequency cycles based on Milakovitch theory: A case study on Miocene Sanya and Meishan Formations in Qiongdongnan Basin[J]. Petroleum Geology and Experiment, 2012, 34(6): 641-647.]
[9] 任金锋,廖远涛,孙鸣,等. 基于小波变换的高精度层序地层定量划分研究及其应用[J]. 地球物理学进展,2013,28(5):2651-2658. [Ren Jinfeng, Liao Yuantao, Sun Ming, et al. A method for quantitative division of sequence stratigraphy with high-resolution based on wavelet transform and its application[J]. Progress in Geophysics, 2013, 28(5): 2651-2658.]
[10] 袁学旭,郭英海,赵志刚,等. 以米氏旋回为标尺进行测井层序划分对比——以东海西湖凹陷古近—新近系地层为例[J]. 中国矿业大学学报,2013,42(5):766-773. [Yuan Xuexu, Guo Yinghai, Zhao Zhigang, et al. Comparison of well-log sequence stratigraphic classification and correlation using Milankovitch cycles: Paleogene-Neogene strata of Xihu sag in East China Sea[J]. Journal of China University of Mining & Technology, 2013, 42(5): 766-773.]
[11] 郭少斌,陈成龙. 利用米兰科维奇旋回划分柴达木盆地第四系层序地层[J]. 地质科技情报,2007,26(4):27-30. [Guo Shaobin, Chen Chenglong. Division of sequence stratigraphy of Quaternary Formation in Qaidam Basin using the Milankvitch Cycle[J]. Geological Science and Technology Information, 2007, 26(4): 27-30.]
[12] 吴淑玉,刘俊. 北黄海东部坳陷始新统米兰科维奇旋回特征[J]. 地球科学,2015,40(11):1933-1944. [Wu Shuyu, Liu Jun. Characteristics of Milankovitch cycle in Eocene Formation, Eastern depression of the North Yellow Sea Basin[J]. Earth Science, 2015, 40(11): 1933-1944.]
[13] 谭先锋,蒋艳霞,李洁,等. 济阳坳陷古近系孔店组高频韵律旋回沉积记录及成因[J]. 石油与天然气地质,2015,36(1):61-72. [Tan Xianfeng, Jiang Yanxia, Li Jie, et al. Sedimentary record and origin of high frequency cycles in the Paleogene Kongdian Formation in the Jiyang depression[J]. Oil & Gas Geology, 2015, 36(1): 61-72.]
[14] Moseley B A, Tsimmer V A. Evolution and hydrocarbon habitat of the South Turgay Basin, Kazakhstan[J]. Petroleum Geoscience, 2000, 6(2): 125-136.
[15] Yin Wei, Fan Zifei, Zheng Junzhang, et al. Characteristics of strike-slip inversion structures of the Karatau fault and their petroleum geological significances in the South Turgay Basin, Kazakhstan[J]. Petroleum Science, 2012, 9(4): 444-454.
[16] 乔彦国,李瑞,漆建华,等. 测井旋回分析在南图尔盖盆地Aryskum坳陷侏罗系地层划分与对比中的应用[J]. 地球物理学进展,2015,30(2):601-606. [Qiao Yanguo, Li Rui, Qi Jianhua, et al. Cyclostratigraphy methods research for Jurassic of Aryskum depression South Turgai Basin[J]. Progress in Geophysics, 2015, 30(2): 601-606.]
[17] Hinnov L A. Cyclostratigraphy and its revolutionizing applications in the earth and planetary sciences[J]. Geological Society of America Bulletin, 2013, 125(11/12): 1703-1734.
[18] Ruddiman W F. Earth's climate: past and future[M]. New York: Macmillan, 2001.
[19] Huang C, Hinnov L, Fischer A G, et al. Astronomical tuning of the Aptian Stage from Italian reference sections[J]. Geology, 2010, 38(10): 899-902.
[20] 黄春菊. 旋回地层学和天文年代学及其在中生代的研究现状[J]. 地学前缘,2014,21(2):48-66. [Huang Chunju. The current status of cyclostratigraphy and astrochronology in the Mesozoic[J]. Earth Science Frontiers, 2014, 21(2): 48-66.]
[21] Sloss L L. Sequences in the cratonic interior of North America[J]. Geological Society of America Bulletin, 1963, 74(2): 93-114.
[22] Vail P R, Mitchum R M, Thompson Iii S. Seismic stratigraphy and global changes of sea level: part 3: Relative changes of sea level from coastal onlap[J]. Antimicrobial Agents & Chemotherapy, 1977, 41(9): 1859-1866.
[23] Vail P R. The stratigraphic signatures of tectonics, eustacy and sedimentology-an overview[J]. Cycles and Events in Stratigraphy, 1991: 617-659.
[24] 梅冥相. 长周期层序形成机制的探索:层序地层学进展之二[J]. 古地理学报,2010,12(6):711-728. [Mei Mingxiang. Research on forming mechanism of long-term sequences: the second advance in sequence stratigraphy[J]. Journal of Palaeogeography, 2010, 12(6): 711-728.]
[25] 梅冥相,高金汉. 岩石地层的相分析方法与原理[M]. 北京:地质出版社,2005:141-151. [Mei Mingxiang, Gao Jinhan. The principle and method of lithostratigraphy phase[M]. Beijing: Geological Publishing House, 2005: 141-151.]
[26] 王鸿祯,史晓颖,王训练,等. 中国层序地层研究[M]. 广州:广东科技出版社,2000:20-25. [Wang Hongzhen, Shi Xiaoying, Wang Xunlian, et al. Research on the sequence stratigraphy of China[M]. Guangzhou: Guangdong Science and Technology Press Guangzhou China, 2000: 20-25.]
[27] 郑荣才,彭军,吴朝容. 陆相盆地基准面旋回的级次划分和研究意义[J]. 沉积学报,2001,19(2):249-255. [Zheng Rongcai, Peng Jun, Wu Zhaorong. Grade division of base-level cycles of terrigenous basin and its implications[J]. Acta Sedimentologica Sinica, 2001, 19(2): 249-255.]
[28] 金之钧,范国章,刘国臣. 一种地层精细定年的新方法[J]. 地球科学,1999,24(4):379-382. [Jin Zhijun, Fan Guozhang, Liu Guochen. A new method for accurate dating of strata[J]. Earth Science, 1999, 24(4): 379-382.]
[29] 刘洋,吴怀春,张世红,等. 珠江口盆地珠—坳陷韩江组—万山组旋回地层学[J]. 地球科学,2012,37(3):411-423. [Liu Yang, Wu Huaichun, Zhang Shihong, et al. Cyclostratigraphy research on the Hanjiang-Wanshan formations in Zhuyi depression, Pearl River Mouth Basin[J]. Earth Science, 2012, 37(3): 411-423.]
[30] 伊海生. 地层记录中旋回层序界面的识别方法及原理[J]. 沉积学报,2012,30(6):991-998. [Yi Haisheng. Detection of cyclostratigraphic sequence surfaces in stratigraphic record: its principle and approach[J]. Acta Sedimentologica Sinica, 2012, 30(6): 991-998.]
[31] 李江涛,李增学,余继峰,等. 基于测井数据小波变换的层序地层对比——以鲁西和济阳地区石炭、二叠系含煤地层为例[J]. 沉积学报,2005,23(4):639-645. [Li Jiangtao, Li Zengxue, Yu Jifeng, et al. Stratigraphic sequence correlation based on wavelet transform of well-logging data: Taking the coal-bearing strata of Permo-carboniferous system in Luxi and Jiyang area as an example[J]. Acta Sedimentologica Sinica, 2005, 23(4): 639-645.]
[32] 田世峰,陈中强,查明. 珠江口盆地中中新世韩江组天文调谐地质年代表[J]. 中国石油大学学报:自然科学版,2012,36(1):27-32. [Tian Shifeng, Chen Zhongqiang, Zha Ming. Astronomical time scale of middle Miocene Hanjiang Formation in Pearl River Mouth Basin, South China Sea[J]. Journal of China University of Petroleum, 2012, 36(1): 27-32.]
[33] 汪品先. 低纬过程的轨道驱动[J]. 第四纪研究,2006,26(5):694-701. [Wang Pinxian. Orbital forcing of the low-latitude processes[J]. Quaternary Sciences, 2006, 26(5): 694-701.]
[34] Laskar J, Robutel P, Joutel F, et al. A long-term numerical solution for the insolation quantities of the Earth[J]. Astronomy & Astrophysics, 2004, 428(1): 261-285.
[35] 吴怀春,张世红,冯庆来,等. 旋回地层学理论基础、研究进展和展望[J]. 地球科学,2011,36(3):409-428. [Wu Huaichun, Zhang Shihong, Feng Qinglai, et al. Theoretical basis, research advancement and prospects of cyclostratigraphy[J]. Earth Science, 2011, 36(3): 409-428.]
[36] 郑荣才,尹世民,彭军. 基准面旋回结构与叠加样式的沉积动力学分析[J]. 沉积学报,2000,18(3):369-375. [Zheng Rongcai, Yin Shimin, Peng Jun. Sedimentary dynamic analysis of sequence structure and stacking pattern of base-level cycle[J]. Acta Sedimentologica Sinica, 2000, 18(3): 369-375.]
Recognition and Division of High-resolution Sequences based on the Milankovitch Theory: A case study from the Middle Jurassic of Well Ary301 in the South Turgay Basin
SHI JuYe1,2,JIN ZhiJun1,3,LIU QuanYou1,3,HUANG ZhenKai1,3
1. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing 100083, China2. School of Energy Resources, China University of Geosciences, Beijing 100083, China3. Petroleum Exploration and Production Research Institute, SINOPEC, Beijing 100083, China
It aims to achieve the division and correlation of high-resolution sequences by integrating the Milankovitch cycles with cycles of different scales so as to introduce such a high precision time scale into the high-resolution sequence stratigraphic classification. This work takes the Well Ary301 in Aryskum graben of the South Turgay Basin in Kazakhstan as an example. Based on different sedimentary characteristics, spectral analysis and continuous wavelet transform are used to Intervals I-IV of natural gamma ray data, respectively, which demonstrate that well-preserved Milankovitch cycles are contained in the sedimentary strata. Aryskum graben deposition process is obviously effected by astronomical orbital period, the formation thickness of 31.9~39.5 m is affected by the long eccentricity of 400 kyr, the formations thickness of 11.9~14.2 m and 6.7~8.8 m are affected by the short eccentricity of 125 kyr and 95 kyr, respectively. Cycle curves analyzed by filtering are compared with the astronomical model theory, which helps establish the Karagansky Formation of floating astronomical time scale. Finally, 11.5 middle term cycles and 47 short term cycles are identified, the filtering curves with eccentricity cycles of 400 kyr and 125 kyr are identified as the reference curves to divide middle term and short term cycles to ensure the scientific and unified division scheme in the study area, and a natural standard unaffected by man-made factors is proposed for high-frequency sequence division.
South Turgay Basin; Milankovitch cycle; spectral analysis; astronomical time scale; high-frequency sequence
1000-0550(2017)03-0436-13
10.14027/j.cnki.cjxb.2017.03.002
2016-05-03; 收修改稿日期: 2016-07-18
石巨业,男,1989年出生,博士,非常规油气地质,E-mail: shijuyeone@163.com
P618.13
A
