基于时间序列的数据流可视化算法的实现与改进
2017-06-01赵焕霞
赵焕霞
摘要:随着信息技术尤其是物联网等技术的发展,人们获取数据的能力也取得了惊人的进展,大量需要处理的数据迅速涌现,形成无法估量的数据量。在源源不断的数据流总挖掘有价值的信息已成为数据挖掘领域需要面对的新挑战。该文对Lucas Lucasa等人提出的时间可视图思想进行了深入的研究,并逐步提出了两种具体实现方法,将其应用在基于时间序列的数据流上,把数据流转化成网络图,从而使得可以利用网络图的拓扑性质,对数据流做进一步的研究,例如相似性查询和趋势预测等。
关键词:数据流;时间序列;可视化;网络拓扑性质
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2017)08-0013-04
1概述
随着硬件条件的飞速提升,以及物联网技术的日新月异,需要处理的数据正以每天数以百万计甚至没有上限的速度增长。例如,电信部门的大型交换机每天可以记录高达几千万条的通话记录,装有GPS部件的整个传感器体系每天传回的海平面高度数据可用TB计算。在这样大的数据量基数和如此飞速的增长速度之下,如果我们仍然采用传统数据库的应用模式来处理数据,这种任务几乎是不可能完成的。基于此种情况,数据流挖掘应运而生,此种解决方案的最大特点是,待处理的数据是以一种动态、流式的形式出现即数据流(data stream),对于数据流中的数据,我们只能按顺序进行一次或有限次的访问。目前,数据流尤其是数据流挖掘已成为业界研究热点之一。
2相关概念
2.1数据流
数据流就是数据量非常大的能够持续到达的、潜在无限的大数据的有序序列。相对于传统数据库中的静态数据,数据流有其特殊的特点:时效性、实时性、无限性和瞬时性等。所以,我们在对数据流做处理时,尤其要注意在时空上的限制,通常采用单一扫描的线性算法处理数据流中的数据,该算法中心思想是用精度换取时间,尽量一次性访问数据即可获得较优解和有价值信息。总而言之,数据流的处理算法对时间和空间复杂度都有很高的要求,本文将针对数据流下一个滑动窗口内的数据集或在流中随机选取的数据集的处理算法的时空复杂度进行重点讨论。
2.2数据流挖掘研究现状
目前,在数据流挖掘方面成果显著的主要有:数据流聚类、分类和频繁模式挖掘。至今在数据流的可视化图领域研究及成果并不显著,在该领域进行深入研究将是一个新的突破点。
2.2.1数据流聚类算法研究
数据流可看作一个随时间的进行而不断变化的无限过程,其隐含的聚类可能随着时间的动态变化而导致聚类质量降低。最近几年以来,有众多的学者对大规模数据集应用了一趟聚类算法,如Squeezer算法和BIRGH算法,这些算法也是可以应用于相应的数据流问题上,也有不少的学者针对数据的聚类提出相应的算法,典型的有STREAM算法和CluStream算法。
2.2.2数据流分类挖掘算法研究
在数据流分类方面成果显著的主要是P.Domingos和G.Hulten的研究。在文献中提出了一种改进的Hoeffding决策树分类算法VFDT(Very Fast Decision Tree),这种算法类似于大多数的机器学习方案,同样都是假设数据是从静态分布中随机获取的,不能反映数据随时间变化的趋势。因此,P.Domingos和G.Huhen在研究中加入了滑动窗口技术,对VFDT算法进行了改进,提出了CVFDT(Concept-adapting Very Fast DecisionTree)算法,该算法仅保留了VFDT算法在速度和精度方面的优点,对数据产生过程中变化趋势的检测和响应做了改进,使得算法能够更好地适应对高速时变流数据的分类。
2.2.3数据流频繁模式挖掘算法研究
针对数据流的频繁模式挖掘,文献提出了基于FP-tree模型的有效算法FP-stream,該算法采用倾斜时间窗口技术维护频繁模式用以解决时间敏感的问题。文献提出了一种利用有限存储空间通过一趟扫描来估计数据流中最大频繁项集的算法,该算法采用了称为“COUNT SKETCH”的数据结构,使其可以在流中对频繁项集的频率进行可靠的估计。
2.3时间序列数据流
要对数据流进行挖掘,首先要了解数据流模型删。数据流D可看作是由连续不断地到达的数据组成的动态增长的数据集,即D={a1,a2,…,ai,…,aj,…},其中ai为数据,如果j>i,则ai先于aj,到达;如果|j-i|=1,则ai与aj相邻。根据ai的描述的不同,数据流模型可以分为以下3类:
(1)时间序列数据流。用其来描述时间序列的数据。这里的ai可以定义为:ai=(i,Ii)其中,Ii为i时刻产生的数据。
(2)Cash Register数据流。该模型应用较为普遍。这里的ai可以定义为:ai=(j,Ii)其中,Ii>=0为新产生的数据,很显然有:ai[j]=ai-1[j]+Ii。此时数据流中的多个数据项增量式的表达一个a[j]。
(3)Turnstile数据流。这种模型可以记录动态的插入和删除操作。这里的ai可以定义为:ai=(j,Ui)其中,Ui可以大于0,也可以小于0,很显然有a[j]=ai-1[j]+Ui。此时,数据流中的多个数据项表达一个a[j].a[j]随着数据的流入,可能会增加,也可能会减小。
本文重点研究第一种数据流模型,即时间序列数据流模型的可视化,以下简称时间序列。
2.4时间序列
为了便于下面的描述和使用,这里对时间序列重新进行以下定义:数据流下的时间序列总是持续不断的,为了便于分析我们把数据固定在一个滑动窗口内或者一个随机选取的样本数据集上,这样可以把时间序列看成某一个时刻数据流的静止状态,然后对其进行快速处理以便于后续的分析工作。这样的时间序列是由实数值和时间的二元对组成的有序集合,记为X={(xl,tl),(x2,t2),…,(xn,tn)},元素(xi,ti)表示时间序列在ti时刻的实数值为xi,且ti是严格递增的。
一般情况下,时间序列的时间间隔△t=ti-ti-1相等,可以看作tl=l,△t=1,此时时间序列可以简记为X={x1,x2,…,xn},长度为n的时间序列X可以看作n维空间上的一个点。
3时间序列的表示方法
目前比较成熟的时间序列的表示方法有:离散傅里叶变换(Discrete Fourier Transform,DFT)、离散小波变换(DiscreteWavelet Transform,DWT)、分段线性表示((Piecewise LinearRepreseutation,PLR)、分段聚合近似(Piecewise Aggregate Ap-proximation,PAA)。
4时间序列的可视化表示方法
4.1可视化思想
Lucas Lucasa等人在2008年提出了一种可视化思想,将时间序列转化成一个无向网络。这个网络继承了时间序列的属性,将对时间序列的分析转化成对网络图的分析。
如图1上半部分,在柱状图中给出了周期性时间序列的前二十个值,对应的数据值在柱状图上面给出。然后把它看作是一个地形,我们认为在一个柱的顶端能够看到的其他柱之间是可连的,这样就得到了一个连通图。在这个图中,经分析可知,相邻的点一定可见,所以任意两点之间都是经过一定的路径连通的,如果两个数据能够连通,则这两个数据的连线不能切断任意其他两个数据的连线。
我们把这个思想加以推广,然后将一系列的描述转化成数学公式,可以得到如下的可视化标准:任意的两个数据(xa,ta)和(xb,tb),对于位于他们中间的任一其他数据(xc,tc)满足:
4.2可视化实现算法之一VG(Visibility Graph)
可视化思想中一个重点之处就在于它将时间序列的柱状图看成一个地形图,用地形的高低起伏的观点来看待问题,因为数据流时效性强,前面一直强调的问题就是我们在处理数据流数据时所用的算法时间复杂度一定要低,这样我们就会考虑到,从第一个数据开始,它有可能看到的数据只能是从这个数据开始往后小于等于它的数据,如果遇到一个大于等于它的数据,就会对后面的数据有所遮挡,因此我们可以将所有的数据按照大小分段以后,再在段内利用以上斜率公式计算出两点之间是否可连,这样就不用计算任意两个数据之间是否可连,只需计算一定范围内有可能可连的那些点即可。这个思路存在一个问题,就是对于前面的数据来说,它看不到大于等于它的后面的数据,由于我们所转化的网络图是无向的,所以后面可能会有某个值很大的数据能够看见它。因此在此算法的结尾,我们将整个时间序列倒置,再进行一遍算法。如果数据集很大的话,即使这样我们仍然觉得这个算法的计算量很合理,因为它不必计算任意两对节点,会尽可能地节省一些时间。但是与此同时,它的空间复杂度会增加。具体算法步骤如下:
%然后对X进行与Y相同的操作,篇幅有限,在此不一一赘述
4.3可视化实现算法之二NVG(New Visibility Graph)
忽视任何分段,直接利用斜率公式计算任意两点之间是否相连,省去了最外面的两层循环。这样得出的算法看起来步骤简单多了,由于少了循环的嵌套,我们可以推断其空间复杂度明显低于VG,但是我们仍然认为它的计算量是个可观的数目,因此继续对这两个算法进行试验比较。具体算法步骤如下:
4.4实验对比
为了将问题尽量简化,这里采用随机序列进行试验来比较两种实现方法。最终得出如下的折线图。从图中可以明显地看出几乎在每个数据集下,NVG的时间复杂度都优于VG,并且比VG更加稳定。接下来我们将使用NVG方法对不同的序列进行转化,并进一步分析。
如下图我们给出了实验中选取的一部分随机序列及其对应的随机序列数据集的度分布。
5通过网络拓扑性质分析时间序列
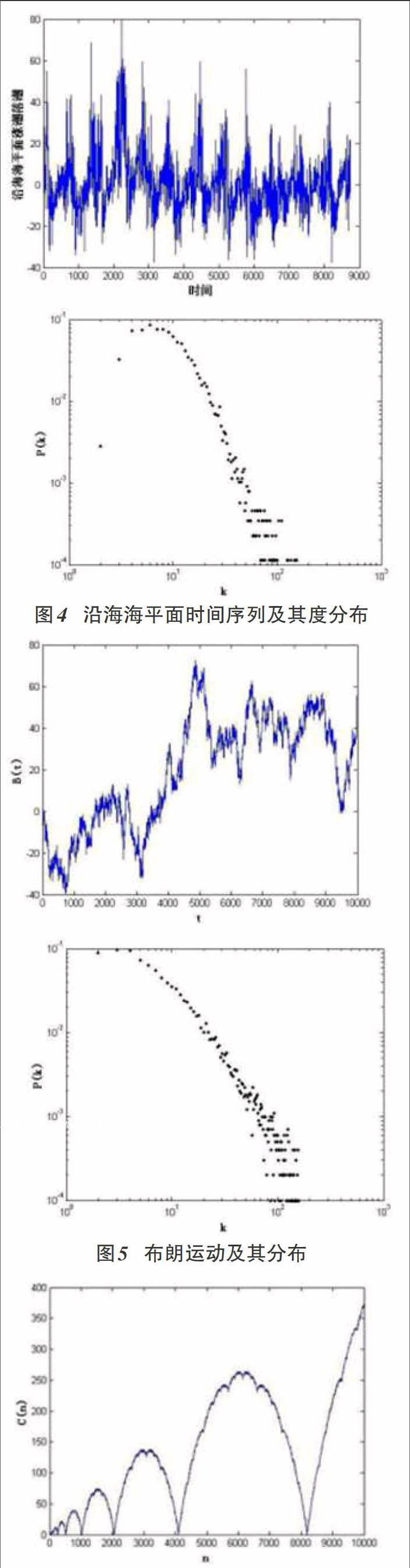
根据所得的无向网络图,我们可以得一些网络拓扑性质,例如节点的度、网络平均度、平均路径长度、聚类系数和度分布等。这里我们以度分布为例,进行简要分析。下面分别给出海浪高度时间序列、沿海海平面时间序列、布朗运动(Brown Motion)、康威运动(ConwaySeries)的时间变化曲线和其利用VG转化成的网络的度分布。
从上图我们可以看出不同的时间序列对应的网络度分布不尽相同,它在一定程度上反映了不同时间序列之间的差异。但是如果仔细观察2、3两幅图的话我们可以看出来他们之间比其他两幅图相似性更大,如果进一步分析的话我们可以得知布朗运动的度分布其实是满足P(k)~k-α幂律分布的,通过进行幂律拟合甚至可以得到α的值,而1、4两幅图又满足什么样的规律呢,有待于进一步研究。
6总结与展望
虽然给出了时间序列转化成网络的方法但是主要的思想还是要研究用这个方法基于图论对时间序列进行分析的可行性达到了一个什么样的程度。通过上文不难看出,周期性的序列转化成了规则的图,随机序列转化成随机图,不规则序列转化成了无标度网络。文中給出的转化方法只是针对无向无权重的网络来进行的,如果换成有向网络又该如何定义,权重大小又该如何取舍,这都将是接下来的研究重点。
另外,前面已经指出时间序列仅仅是数据流模型的一种,这一方法是否适用于其他几种模型还有待于进一步研究,总之,这一可视化思想为数据流挖掘研究提供了新的思想,开拓了新的领域。